UNIT 1

Sets & Propositions

Question-1: If A = {1, 2, 3, 4, 5, 6}, B = {4, 5, 6, 7, 8, 9} and C = {5, 6, 7, 8, 9, 10}

Then-

A∪B = {1, 2, 3, 4, 5, 6, 7, 8, 9}

A∪C = {1, 2, 3, 4, 5, 6, 7, 8, 9,10}

B∪C = {4, 5, 6, 7, 8, 9, 10}

A∩B = {4, 5, 6}

A∩C = {5, 6}

B∩C = {5, 6, 7, 8, 9}

Question-2: Define sets.

Sol.

A set is a collection of well-defined objects which are called the elements or members of the set.

We generally use capital letters to denote sets and lowercase letters for elements.

If any element which exists in the set is to be denoted as-

Suppose an element ‘a’ is from a set X, then it is represented as- a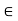X

Which means the element ‘a’ belongs to the set X.

If the element is not form the group then we use ‘not belongs to’.

Question-3: Define union and intersection.

Sol.

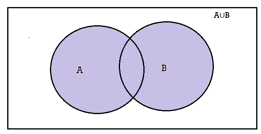
Union- We denote union of two sets as- A∪B, which is the set of all elements which belongs to A or to B.

That is-

                                       A∪B = {x | x∈∅A or x∈∅B}

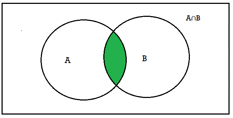
Intersection- We denote intersection of two sets as- A∩B, which is the set of all elements which belongs to A and to B.

That is-

                                        A∩B = {x | x∈∅A and x∈∅B }

Note- Two sets are said to be disjoint if they have no common elements in common.

Question-4: What are the multi-sets?

Sol.

A multi-set is a generalization of a set where repetition of elements matters.

Like {4, 5, 6} and {5, 4, 6} are the same multi-set but the set {5, 5, 4, 6} is the different multi-set as there is repetition of the elements.

So that, “A multi-set is a set-like, unordered collection where multiplicity(repetition) of the elements matters.

Here multiplicity means how many times an element occurs in the set.

Notation-

If an element ‘a’ occurs ‘n’ times in a multi-set A then it can be represented as - .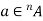

For example-

, ,

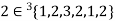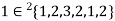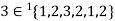
Question-5: Find the number of students at a college choosing at least one of the subject from mathematics, physics and statistics.

The data is given as-

65 study maths, 45 study physics, 42 study statistics

20 study maths and physics, 25 study maths and statistics, 15 study physics and statistics and 8 study all the three subjects.

Sol.

Here we need to find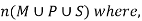

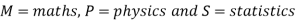
Now by using Inclusion-Exclusion principle-

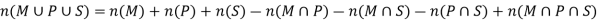
Which gives-

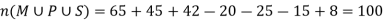
Therefore, we find that 100 students study at least one of the three subjects.

Question-6: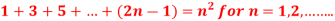

Sol. here for n = 1,     1 = 1²

Now let us assume that the statement is true for n = k

Hence we assume that 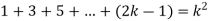is true.

Now we need to prove that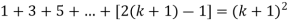

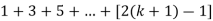
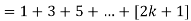
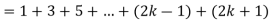
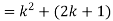
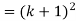
So that 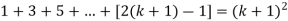which satisfies the second step.

Hence-

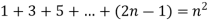
Question-7: Prove the following by using the principle of mathematical induction for all n ∈ N-

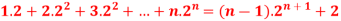
Sol. Here, n = 1, 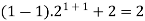, which is true

Step-1: Assume n = k holds-

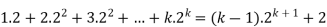
Now show n = k + 1 also holds-

Consider-

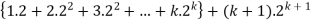
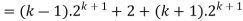
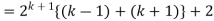
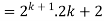
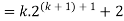
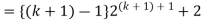
Which is also true for n = k + 1.

Hence proved.

Question-8: define preposition.

Sol.

A proposition (or statement) is a declarative statement which is true or false, but not both.

Example-

(i) Ice floats in water.

(ii) China is in Europe

(iii) 2 + 2 = 4

(iv) 2 + 2 = 5

Compound proposition-

Many propositions are composite, that is, composed of sub-propositions and various connectives discussed

Subsequently such composite propositions are called compound Propositions. A proposition is said to be primitive

if it cannot be broken down into simpler propositions, that is, if it is not composite.

Following two propositions are composite:

“Roses are red and violets are blue.” and “John is smart or he studies every night.”

Basic logical operations-

1. Conjunction- p ⋀ q

Any two propositions can be combined by the word “and” to form a compound proposition called the conjunction of the original propositions. Symbolically,

p ∧ q

Read “p and q,” denotes the conjunction of p and q. Since p ∧ q is a proposition it has a truth value, and this truth

Value depends only on the truth values of p and q.

Note- If p and q are true, then p ∧ q is true; otherwise p ∧ q is false.

2. Disjunction, p ∨ q

Any two propositions can be combined by the word “or” to form a compound proposition called the disjunction of the original propositions. Symbolically,

p ∨ q

Read “p or q,” denotes the disjunction of p and q. The truth value of p ∨ q depends only on the truth values of p

And q as follows-

If p and q are false, then p ∨ q is false; otherwise p ∨ q is true

Negation-

Given any proposition p, another proposition, called the negation of p, can be formed by writing “It is not true that . . .” or “It is false that . . .” before p or, if possible, by inserting in p the word “not.” Symbolically, the negation of p, read “not p,” is denoted by

                                                         ￢p

The truth value of ￢p depends on the truth value of p as follows-

If p is true, then ￢p is false; and if p is false, then ￢p is true

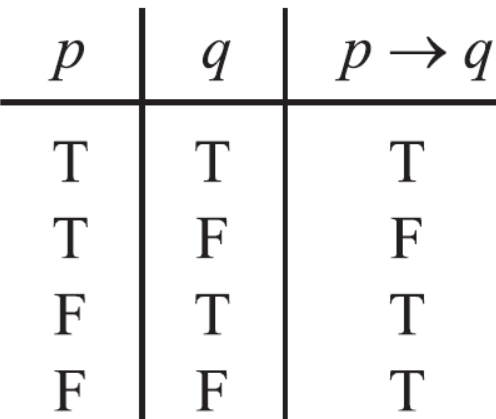
Question-9: What are conditional and bi-conditional statement?

Sol.

The statements are of the form “if p then q”. such statements are called conditional statement and these are denoted by-

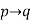
We read it as p implies q.

And another statement is of the form “p if and only if q”, such statement are called bi-conditional statement and it is denoted by-

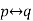
The truth value for conditional and bi-conditional value are given in the following tables-

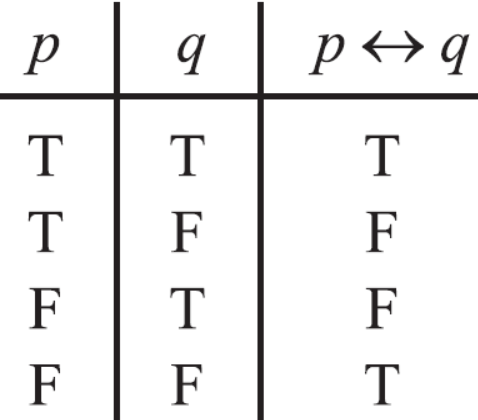
Question-10: Define universal and existential quantifiers.

Sol.

Universal quantifier-

Let p(x) is a propositional function defined on a set A, consider the expression

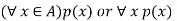
Here the symbol which we read “for all” or “for every” is called universal quantifier.

The above statement can be written as-

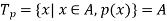
That is, that the truth set of p(x) is the entire set A.

The expression p(x) is an condition itself and it has no truth value

Example: The preposition (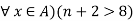 is false since {n |  n + 2 > 8} = {7, 8, …..} ≠ N

Existential quantifier-

Let p(x) be a propositional function defined on a set A. consider an expression-

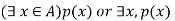
The symbol 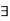reads as there exists is called existential quantifier.