UNIT 2
Combinatorics & Discrete probability
Question-1: In how ways can be drawn an ace or a king from an ordinary deck of playing cards?
Solution:
Number of Aces in a pack = 4
Number of kings in a pack = 4
Number ways an Ace or a king can be drawn from the pack = 4 + 4 = 8
Question-2: In how many different ways one can answer all the questions of a true-false test consisting of 4 questions?
Solution: There are two ways of answering each of the 4 questions. Therefore by product rule the
Number of ways in which all the 4 questions can be answered-
= 2 × 2 × 2 × 2 = 16
Question-3: Three cards are chosen one after the other from a 52-card deck. Find the number m of ways
This can be done: (a) with replacement; (b) without replacement.
Sol.
(a) Each card can be chosen in 52 ways. Thus m = 52(52)(52) = 140 608.
(b) Here there is no replacement. Thus the first card can be chosen in 52 ways, the second in 51 ways, and the third in 50 ways. So that-
P(52, 3) = 52(51)(50) = 132 600
Question-4: A box contains 10 light bulbs. Find the number n of ordered samples of:
(a) Size 3 with replacement,
(b) Size 3 without replacement.
Solution:
(a) n = 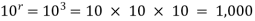
(b) P (10, 3) = 10 × 9 × 8 = 720
Question-5: Find the number of ways of placing 8 similar balls in 5 numbered boxes.
Solution:
The number of ways of placing similar balls in 5 numbered boxes is
= C (5 – 1 + 8, 8)
= C (12, 8) = 495
Question—6: In a college counselling, 30 students are choosing maths, 20 are choosing Computer science and 10 are selecting maths and computer science.
Suppose a student is selected randomly from 100 students then find the probability that student choose maths or computer science.
Sol.
Let A = {student is taking maths} and B = {student taking computer science}
So that the probabilities will be-
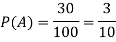
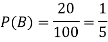
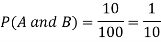
Hence by the addition principle of probability-
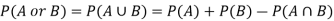
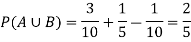
Question-7: The probability of A hits the target is 1 / 4 and the probability that B hits the target is 2/ 5. If both shoot the target then find the probability that at least one of them hits the target.
Sol.
Here it is given that-
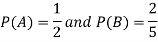
Now we have to find- 
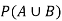
Both two events are independent. So that-
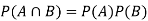
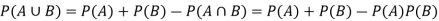
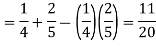
Question-8: An urn I contains 3 white and 4 red balls and an urn II contains 5 white and6 red balls. one ball is drawn at random from one of the urns and is found to be white.
Find the probability that it was drawn from urn I.
Sol. Let
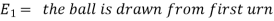
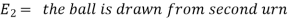
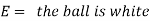
Now we have to find-
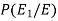
So that by using Bayes theorem, we get-
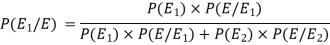
Here,
Two urns are equally likely to select,
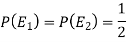

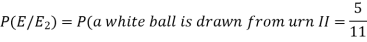
So that-
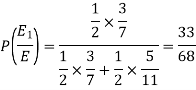
Question-9:
In a bolt factory, machines A, B and C manufacture respectively 25%, 35% and 40% of the total. If their output 5, 4 and 2 per cent are defective bolts. A bolt is drawn at random from the product and is found to be defective. What is the probability that it was manufactured by machine B?
Sol. here-
A: bolt is manufactured by machine A
B: bolt is manufactured by machine B
C: bolt is manufactured by machine C
So that- P(A) = 0.25, P(B) = 0.35 and P(C) = 0.40
The probability of drawing a defective bolt manufactured by machine A is P(D/A) = 0.05
P (D/B) = 0.04 and P (D/C) = 0.02
Therefore by using Bayes theorem-
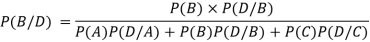
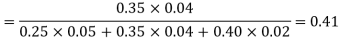
Question-10: Define permutations and combinations.
Sol.
The arrangement of a set of n objects in a given order is called a permutation.
Any arrangement of any 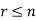 of these objects in a given order is said to be r-permutation.
of these objects in a given order is said to be r-permutation.
The number of permutations of n objects taken r will be denoted as-
P(n, r)
Formula- 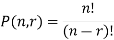
Permutation with repetitions-
The number of permutations of n objects of which are 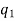 are alike,
are alike, 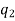 are alike,
are alike, 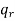
are alike is-
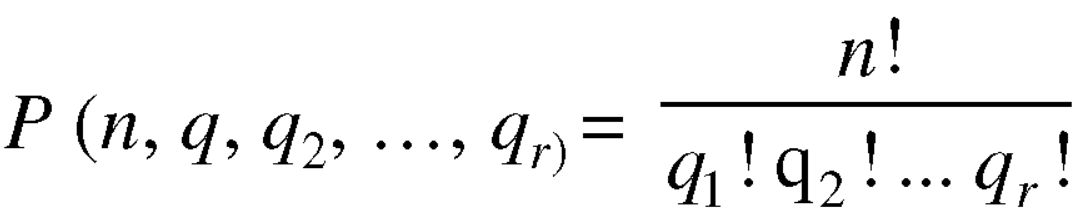
Combinations-
A combination of n objects taken at a time is an unordered selection of r of the n
Objects (r ≤ n).
A combination of n objects taken r at a time is also called r-combination of n objects.
The number of combinations is given by-
C(n, r)
Note-
1. property-1
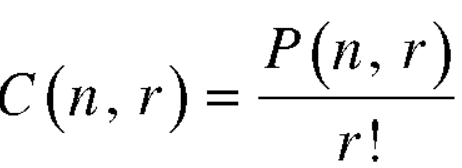
2. property-2
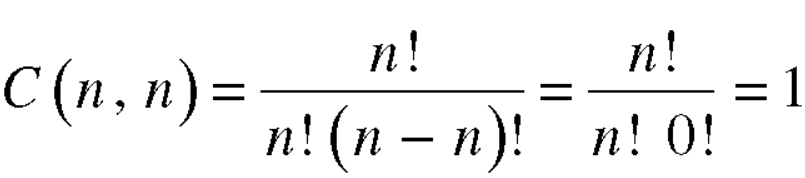
3. property-3