Unit 3

Graph theory

Question-1: Define Graph.

Sol.

A graph G is an ordered pair (V, E) where V is a non-empty set and E is the set of edges in which each element of E is assigned to a unique unordered pair of elements of V.

An element of a set E is generally denoted as- e = (v,u) where u, v ∈ V.

U and v are called the end vertices of edge e.

Question-2 Consider the graphs given below-

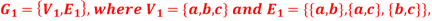
 Check whether these graphs are same or not?

Sol.

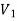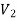As we can see that these graphs are not same because here and are not same since 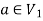but a does not belongs to .

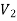These two graphs look same but not equal.

We can draw these graphs as below-

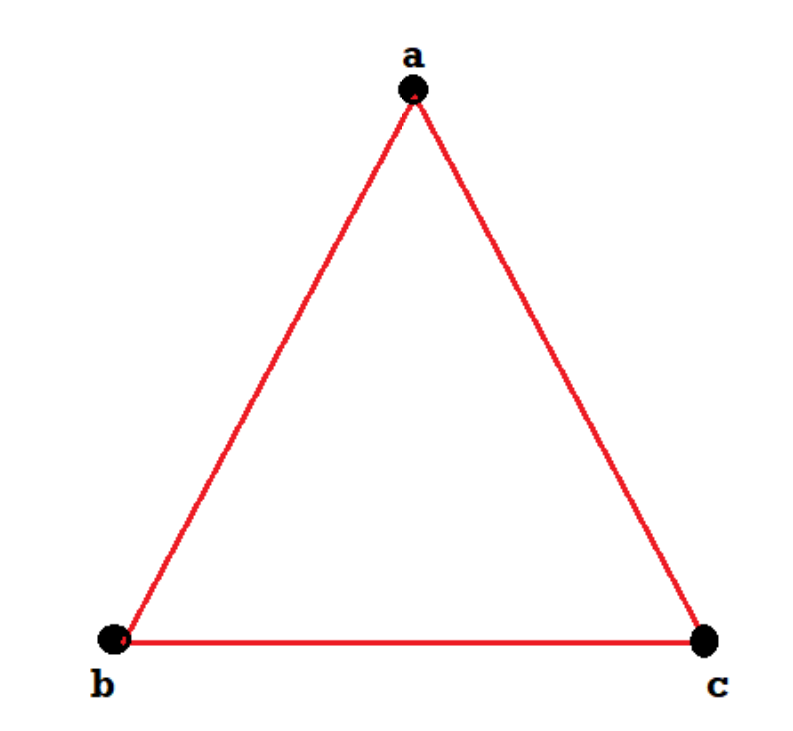
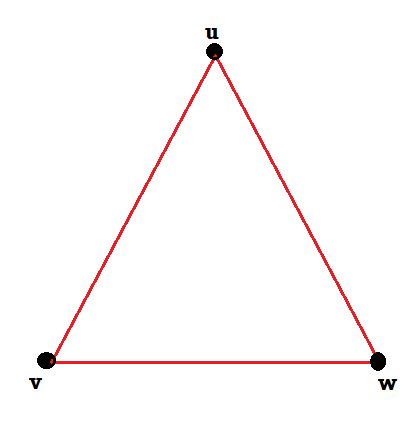
These types of graphs are known as isomorphic graph when they are same except for the name of vertices.

Question-3: What are weighted graphs?

Sol.

A graph G is said to be a weighted graph if each edge e of G is assigned a non-negative number w(e) called the weight of v.

The weighted graph is given below-

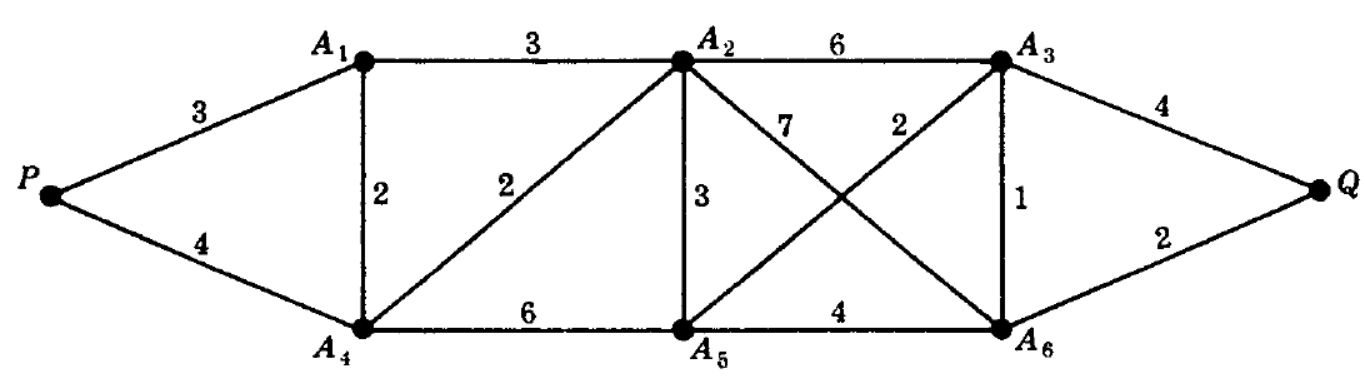
Question-4: Define sub-graph and isomorphic graph.

Sol.

sub-graph-

We can say that 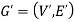is a sub-graph of G = (V, E), and write 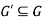provided .

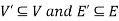We can say that 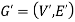is an induced sub-graph of G = (V, E), provided 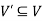and every edge in E whose vertices are still in 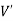is also an edge in .

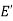Isomorphic graphs-

Let 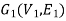and 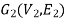be two graphs. The graph 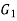and 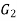are said to be isomorphic if there is a bijective function 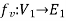such that if u and v are end vertices of some edge e ∈ 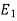then 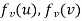end vertices of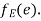

Question-5: Define bipartile graph.

Sol.

A graph G(V, E) is said to be bipartite, if the vertex set V can be partitioned in to two non-empty disjoint subset 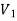and 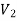such that each edge is G had end vertex is 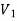and other end vertex in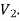

There is no edge between two vertices of 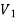as well as there is no edge between two vertices of .

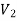Here 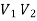bipartition of V.

Question-6: What are Hamiltonian graph and Eulerian graph?

Sol.

Eulerian graph- A graph G is called an Eulerian grap

h if there exists a closed transversal trail, called an Eulerian trail.

Hamiltonian graph- A closed path that visits every vertex in G exactly once and if G admit a Hamiltonian circuit, then G is called Hamiltonian graph.

Note- An Eulerian  circuit traverses every edge exactly once, but many repeats vertices.

While a Hamiltonian circuit visits each vertex exactly once but many repeats edges.

Following are the examples of Hamiltonian and Eulerian graph respectively-

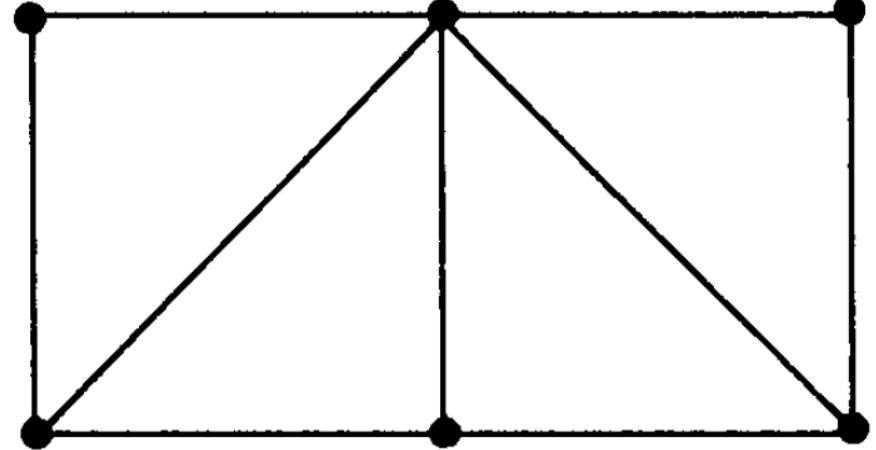
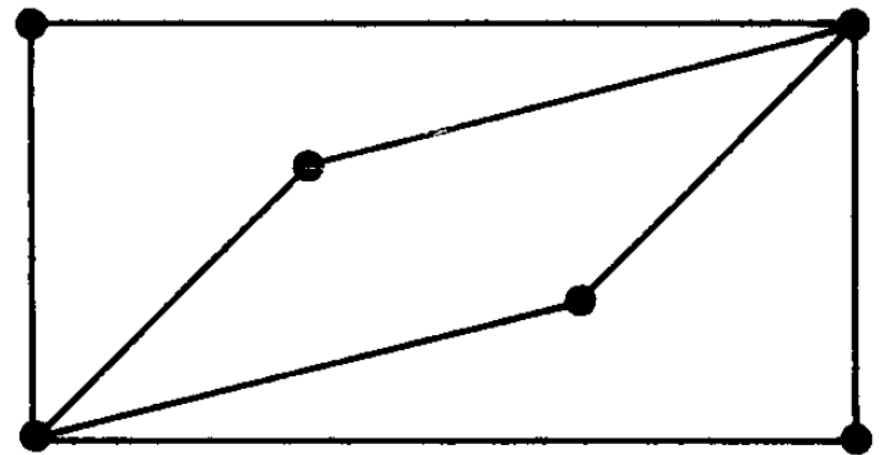
Question-7: Define planar graph.

Sol.

When a connected graph can be drawn without any edges crossing, it is called planar.

When a planar graph is drawn in this way it divides the plane into region called faces.

The following graph is a planar graph-

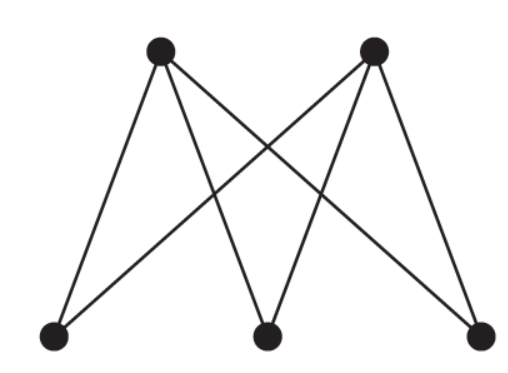
We can draw it like this-

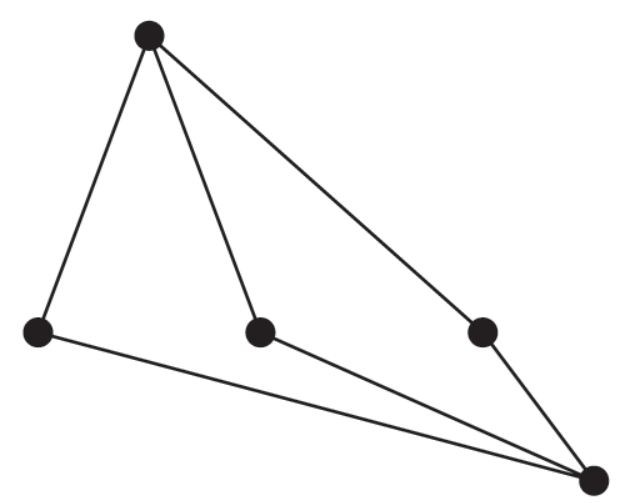
Euler’s formula for planar graph-

For any planar graph with v vertices, e edges and f faces, we have-

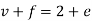
Question-8: Explain why every tree is a bipartite graph.

Solution.

To show that a graph is bipartite, we must divide the vertices into two sets A and B so that no two vertices in the same set are adjacent. Here is an algorithm that does just this.

Designate any vertex as the root. Put this vertex in set A. Now put all of the children of the root in set B. None of these children are adjacent (they are siblings), so we are good so far. Now put into A every child of every vertex in B (i.e., every grandchild of the root). Keep going until all vertices have been assigned one of the sets, alternating between A and B every “generation.” That is, a vertex is in set B if and only if it is the child of a vertex in set A.

Question-9: Define fundamental circuit.

Sol. Fundamental Circuits-

1. The addition of a chord to a spanning tree creates precisely one circuit.

2. The collection of these circuits w.r.t. a particular spanning tree is a set of fundamental circuits.

3. Any arbitrary circuit of the graph may be expressed as a linear combination of the fundamental circuits using the operation ringsum.

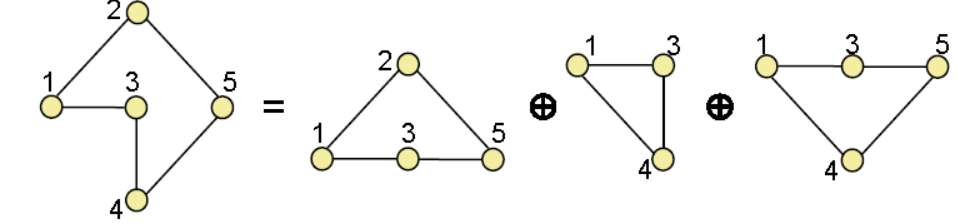
Examples:

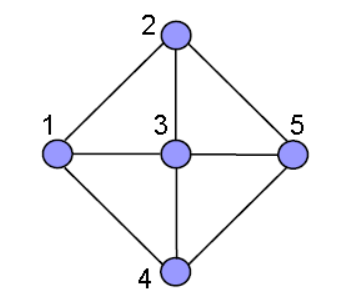
Circuit of G expressed with fundamental circuits-

Question-10: What are the applications of theory?

Sol.

Graph Theory is used in modelling and solving a lot of real world problems, games and puzzles. Here we discuss a very famous puzzle ” The Instant Insanity ” problem.

The goal of this post is to demonstrate that such complicated problem statements can be so easily modeled and solved using Graph Theory. Also I would like to build some more interest into Graph Theory.

The history of graph theory may be specifically traced to 1735, when the Swiss mathematician Euler solved the Konigsberg bridge problem.

The Konigsberg bridge problem was an old puzzle concerning the possibility of finding a path over every one of seven bridges that span a forked river flowing past an island—but without crossing any bridge twice. Euler argued that no such path exists. His proof involved only references to the physical arrangement of the bridges, but essentially he proved the first theorem in graph theory.