UNIT-4
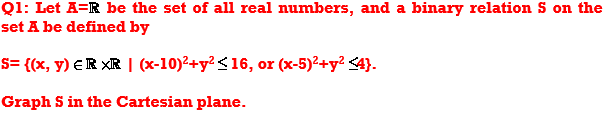
Solution: Recall from analytic geometry that a Cartesian plane is a plane with the normal x and y axis, and a circle of radius r centred at the coordinates (a,b) is given precisely by the equation
(x-a)2 +(y-b)2= r2.
Hence the equation
(x-10)2+y2=16 (=42),
represents a circle of radius 4 centred at the coordinates (10,0), and
(x-5)2+y2=4 is a circle of radius 2 centred at the coordinates (5,0).
Thus, S is the union of these 2 disks, and is represented by the shaded area in the graph below.

Solution:
(2,2): 2-2=0 is even, hence the loop at vertex labelled by 2  A.
A.
(1,3): 1-3=-2 is even, hence the arrow from vertex 1 to vertex 3.
Q3: Use algorithm 1 to find the transitive closure of these relations on {1,2,3,4}.
Solution a): {(1,2), (2,1), (2,3), (3,4), (4,1)}
Transitive Closure
= 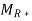
=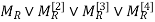

b). {(2,1), (2,3), (3,1), (3,4), (4,1), (4,3)}
Transitive Closure
= 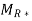
=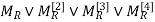

Q4: Use Warhsall’s algorithm to find the transitive closure of these relations on {1,2,3,4}
Solution a). {(1,2), (2,1), (2,3), (3,4), (4,1)}
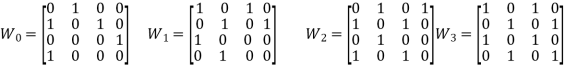
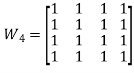
b). {(2,1), (2,3), (3,1), (3,4), (4,1), (4,3)}
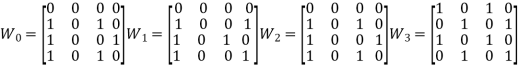
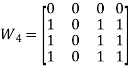
Q5: If R is an equivalence relation on any non-empty set A, then the distinct set of equivalence classes of R forms a partition of A.
Solution Proof: Suppose R is an equivalence relation on any non-empty set A. Denote the equivalence classes 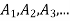
WMST 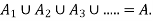
First, we will show 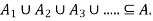
If x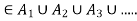 then x belongs to at least one equivalence class,
then x belongs to at least one equivalence class, 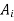 by definition of union.
by definition of union.
By the definition of equivalence class, x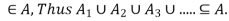
Next, we show 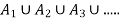
If x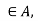 then xRx since R is reflexive. Thus x
then xRx since R is reflexive. Thus x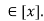
[x]=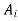 , for some I since [x] is an equivalence class of R.
, for some I since [x] is an equivalence class of R.
So,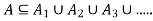 by definition of subset, And so,
by definition of subset, And so, 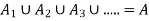 ,
,
by the definition of equality of sets.
Now WMST {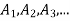 } is pairwise disjoints.
} is pairwise disjoints.
For any i,j, either 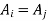 or
or 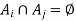 by lemma So,
by lemma So, 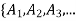 } is mutually disjoint by definition of mutually disjoint.
} is mutually disjoint by definition of mutually disjoint.
We have demonstrated both conditions for a collection of sets to be a partition and we can conclude if R is an equivalence relation on any non-empty set A, then the distinct set of equivalence classes of R forms a partition of A.
Q6: If A is a set with partition P = 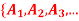 }and R is a relation induced by partition P, then R is an equivalence relation.
}and R is a relation induced by partition P, then R is an equivalence relation.
Solution: Proof: Let A be a set with partition P = 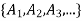 and R be a relation induced by partition P. WMST R is an equivalence relation.
and R be a relation induced by partition P. WMST R is an equivalence relation.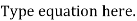
Reflexive
Let 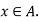 Since the union of the sets in the partition P=A, x must belong to at least one set in P.
Since the union of the sets in the partition P=A, x must belong to at least one set in P.
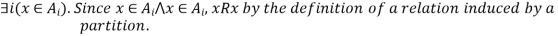
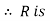 Reflexive
Reflexive
Symmetric
Suppose xRy. 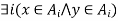 by the definition of a relation induced by a partition.
by the definition of a relation induced by a partition.
Since 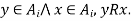
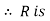 symmetric.
symmetric.
Transitive
Suppose xRy 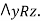
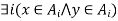 and
and 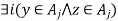 by the definition of a relation induced by a partition.
by the definition of a relation induced by a partition.
Because the sets in a partition are pairwise disjoint, either 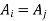 or
or 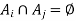 .
.
Since y belongs to both these sets, 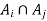
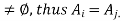
Both x and z belong to the same set, so xRz by the definition of a relation induced by a partition.
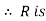 transitive.
transitive.
We have shown R is reflexive, symmetric and transitive , so R is an equivalence relation on set A.
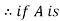 a set with partition P =
a set with partition P = 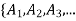 } and R is a relation induced by partition P, then R is an equivalence relation….
} and R is a relation induced by partition P, then R is an equivalence relation….
Q7: a lattice L is modular  a
a  [ b
[ b (
( )] = ( a
)] = ( a  b)
b)  (a
(a  c),
c),  a, b,c
a, b,c  L., a
L., a  c.
c.
solution: suppose L is a modular lattice.
Claim: a 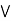 [ b
[ b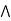 (
(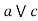 )] = (a
)] = (a 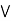 b)
b) 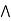 (a
(a 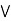 c).
c). 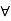 a, b,c
a, b,c 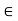 L., a
L., a 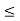 c.
c.
Let a, b, c 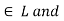 a
a 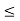 c.
c.
Consider,
a 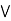 [ b
[ b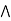 (
(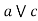 )] = a
)] = a 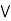 [ b
[ b 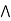 x], let x = a
x], let x = a 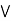 c
c
= (a 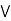 b)
b) 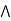 x
x 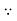 by modular property.
by modular property.
= (a 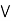 b)
b) 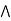 (a
(a 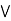 c).
c).
a 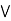 [ b
[ b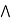 (
(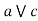 )] = (a
)] = (a 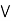 b)
b) 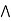 (a
(a 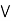 c).
c).
conversely, suppose that
a 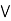 [ b
[ b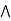 (
(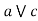 )] = (a
)] = (a 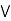 b)
b) 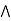 (a
(a 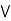 c).
c). 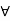 a, b, c
a, b, c 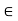 L., a
L., a 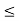 c.
c.
claim: L is modular lattice.
It is enough to prove that a 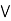 [ b
[ b 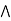 c] = (a
c] = (a 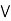 b)
b) 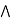 c.
c. 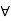 a, b, c
a, b, c 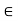 L., a
L., a 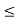 c.
c.
Let a, b, c 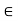 L ; a
L ; a 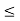 c.
c.
a 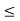 c = a
c = a 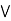 c = c
c = c
= a 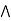 c = a.
c = a.
Consider,
a 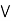 [ b
[ b 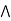 c] = (a
c] = (a 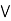 [b
[b 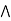 (a
(a 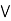 c)].
c)].
= (a 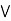 b)
b) 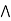 (a
(a 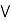 c)
c)
= (a 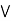 b)
b) 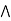 c.
c.
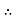 a
a 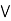 [ b
[ b 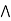 c] = (a
c] = (a 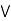 b)
b) 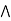 c.
c.
 L is a modular lattice.
L is a modular lattice.
Hence proved.
Q8: every chain is a distributive lattice.
Solution: Proof: suppose L is a chain.
Let a, b, c 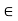 L., a
L., a 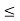 c.
c.
Claim: L is distributive lattice.
It is enough to prove that
a 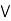 [ b
[ b 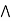 c] = (a
c] = (a 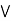 b)
b) 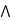 (a
(a 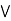 c).
c).
case 1: b 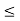 c.
c.
(a 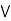 b)
b) 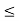 (a
(a 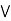 c).
c).
(a 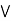 b) = (a
b) = (a 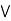 b)
b) 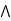 (a
(a 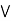 c).
c).
a 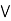 [ b
[ b 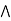 c] = (a
c] = (a 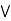 b)
b) 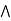 (a
(a 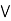 c).
c).
case 2: c 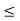 b.
b.
(a 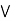 c)
c) 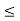 (a
(a 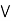 b).
b).
a 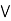 [ c
[ c 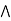 b] = (a
b] = (a 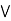 b)
b) 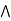 (a
(a 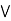 c).
c).
a 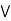 [ b
[ b 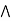 c] = (a
c] = (a 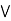 b)
b) 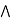 (a
(a 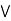 c).
c). 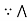 is commutative.
is commutative.
 every chain is a distributive lattice.
every chain is a distributive lattice.
Q9: A maximal chain in a finite nonempty poset must contain a maximal element of S (and a minimal element).
Solution: Poof: Suppose C ⊂ P is a maximal chain, Since (C, 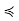 ) is a finite nonempty poset in its own right, it has some maximal element x; since C is totally ordered, the nonexistence of any y in C such that x
) is a finite nonempty poset in its own right, it has some maximal element x; since C is totally ordered, the nonexistence of any y in C such that x 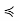 y implies that y
y implies that y 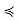 x for all y ∈ C, so x is in fact a greatest element of C (if not necessarily of S). We have two possibilities to address: x may be maximal in S, or it may not. If it is maximal, our condition has been shown. If it is not maximal, there is a z ∈ S such that x
x for all y ∈ C, so x is in fact a greatest element of C (if not necessarily of S). We have two possibilities to address: x may be maximal in S, or it may not. If it is maximal, our condition has been shown. If it is not maximal, there is a z ∈ S such that x 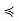 z. Then, for all y ∈ C, y
z. Then, for all y ∈ C, y 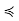 x
x 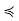 z, so
z, so
y 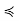 z, so C ∪ {z} is totally ordered, contradicting C’s maximality. The proof for minimal elements proceeds along similar lines.
z, so C ∪ {z} is totally ordered, contradicting C’s maximality. The proof for minimal elements proceeds along similar lines.
Q10: The set of maximal elements of a finite poset S is a maximal antichain; likewise, the set of minimal elements of a finite poset S is a maximal antichain.
Solution: Proof. Note that this is trivially true if S is empty; henceforth, we will consider the case where S has at least one element. Let A be the set of maximal elements of S. We shall first prove that A is an antichain, and then that any augmentation of A by adding an element is not an antichain.
Consider distinct elements x, y ∈ A. Since x is a maximal element and y 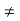 x, maximality guarantees x
x, maximality guarantees x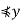 , Likewise, since y is maximal and distinct from
, Likewise, since y is maximal and distinct from
x, y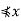 . Thus, x and y are incomparable. Since this is true of arbitrarily chosen distinct elements of A, all distinct elements of A are incomparable and A is an antichain.
. Thus, x and y are incomparable. Since this is true of arbitrarily chosen distinct elements of A, all distinct elements of A are incomparable and A is an antichain.
Now, consider z0 ∈ S −A; that is, z0 is a non-maximal element of S. We shall show that A∪ {z0} is not an antichain. Since z0 is nonmaximal, there is some 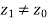 such that
such that 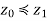 . If z1 is maximal, it is in A; if it is nonmaximal, there is a
. If z1 is maximal, it is in A; if it is nonmaximal, there is a 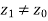 such that
such that 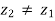 . We continue along these lines until we get either a zk that is maximal, or an infinite ascending sequence z0
. We continue along these lines until we get either a zk that is maximal, or an infinite ascending sequence z0  z1
z1  · · · The latter situation was shown last week to be impossible in a finite poset,
· · · The latter situation was shown last week to be impossible in a finite poset,
Thus, some zk is maximal, so zk ∈ A and z0  z1 · · ·
z1 · · ·  zk gives z0
zk gives z0 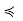 zk by transitivity. Since z0 and zk are comparable, and zk ∈ A, A ∪ {z0} is not an antichain. The proof for minimal elements proceeds along similar lines
zk by transitivity. Since z0 and zk are comparable, and zk ∈ A, A ∪ {z0} is not an antichain. The proof for minimal elements proceeds along similar lines
Q11: Let f(x)=x+2 and g(x)=2x+1.
Here find (fog)(x) and (gof)(x).
Solution: (fog)(x)=f(g(x)) =f(2x+1) =2x+1+2=2x+3
(gof)(x)= g(f(x)) = g(x+2) = 2(x+2) +1 = 2x+5
Hence, (fog)(x)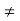 (gof)(x)
(gof)(x)
Some facts about Composition:
Q12: Prove that a function f: defined by f(x)=2x-3 is a bijective function.
defined by f(x)=2x-3 is a bijective function.
Solution: We have to prove this function is both injective and surjective.
If f (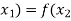 ), then
), then 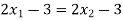 and it implies that
and it implies that 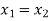
Hence, f is injective.
Here, 2x-3=y
So, x = 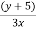 which belongs to R and f(x)=y
which belongs to R and f(x)=y
Hence, f is surjective.
Since f is both surjective and injective, we can say f is bijective.
Q13: let  and domain of f(x) : {x/x
and domain of f(x) : {x/x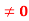 }, domain of g(x): {x/ x
}, domain of g(x): {x/ x }
}
Solution: 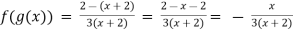
 Domain of f(g(x)) = {x/x
Domain of f(g(x)) = {x/x  -2}
-2}
= 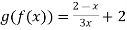 =
= 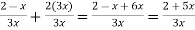
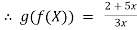
Q14: given f(x) = x+2 and g(x) = 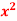 + 1 find [f o g](x) = ?
+ 1 find [f o g](x) = ?
Solution: [f o g] (x) = f [g(x)]
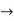 [f o g] (x) = f [ x2 + 1]
[f o g] (x) = f [ x2 + 1]
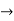 [f o g] (x) = (x2 + 1) +2
[f o g] (x) = (x2 + 1) +2
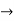 [f o g] (x) = x2 + 3.
[f o g] (x) = x2 + 3.
Q15: find inverse function of the given function f(x) = 4 – 7x.
Solution: given, f(x) = 4 – 7x
Let y = 4 – 7x let y = f(x)
7x = 4 – y
X = 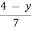 x in terms of y
x in terms of y
f-1(x) = 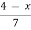 change y to x
change y to x
16: 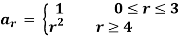 and
and 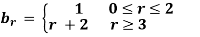
Solution: 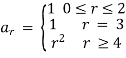 and
and 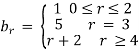
Now we show sum and product of the above numeric functions.
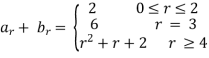 and
and 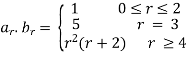
17: solve the difference equation to find the total solution
 …..equation(1)
…..equation(1)
Solution: the homogenous of this equation is obtained by putting R.H.S equal to zero i.e., 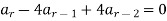
Then equation (1) can be written as,
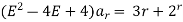
The particular solution is given as
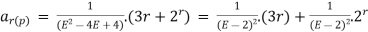
= 3.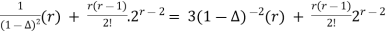
= 3(1+2 ). [r]+
). [r]+ 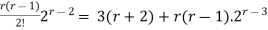
 = 3(r+2) + r(r-1)2r-3
= 3(r+2) + r(r-1)2r-3
Therefore, the total solution is 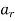 =
= 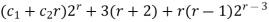 .
.
Q18: Suppose the weights of four students are shown in the following table.
Student | 1 | 2 | 3 | 4 |
Weight | 120 | 100 | 150 | 130 |
Solution: The pairing of the student number and his corresponding weight is a relation and can be written as a set of ordered-pair numbers.
W = {(1,120),(2,100),(3,150),(4,130)}
The set of all first elements is called the domain of the relation.
The domain of W = {1,2,3,4}
The set of second elements is called range of the relation.
The range of W = {120,100,150,130}