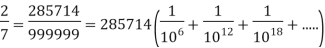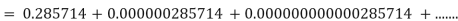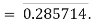UNIT-5
INTRODUCTION TO NUMBER THEORY.
Q 1: Using division algorithm solve the following equation  .
.
Solution: = 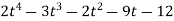
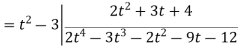
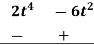
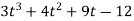
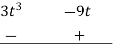

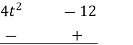
0
Q 2: Use the division algorithm to find q&r such that a= bq +r where
1): a =25 and b =7
2): a =9 and b =4
3): a =203 and b = 8
4): a=150 and b=6
Solution:
1). a = bq+r 2). a =bq+r 3). a = bq+r 4). a = bq+r
25 = 7q+6 9 = 4q+r 203 = 8q+r 150= 6q+r
25 = 7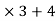
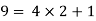
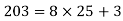
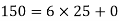

Q 3: Find the greatest common divisor (or HCF) of 128 and 96.
Solution: By the method of prime factorization,
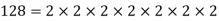
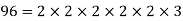
HCF (128,96) = 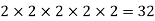
(Or)
By the method of division,
96)128(1
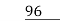
32)96(3
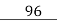
0
Hence, 32 is the HCF of 128 and 96
(or)
By Euclid’s division algorithm,
128 = 96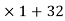
96 = 32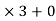
Hence, the HCF of 128 and 96 is 32.
Q 4: Two rods are 22 m and 26 m long. The rods are to be cut into pieces of equal length. Find the maximum length of each piece.
Solution: HCF or GCD is the required length of each piece.
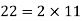
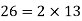
HCF or the greatest common divisor = 2
Hence, the required maximum length of each piece is 2 m.
Q 5: Find the greatest common factor of 24, 148 and 36.
Solution: Prime factorization of given numbers is
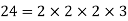
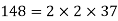
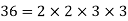
Greatest common factor = 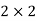 = 4.
= 4.
Q 6: m = 65, n = 40
Solution:
Step 1: The (usual) Euclidean algorithm:
(1): 65 = 1.40 + 25
(2): 40 = 1.25+15
(3): 25 = 1.15+10
(4): 15 = 1.10 + 5
10 = 2.5
Therefore gcd (65,40) = 5.
Step 2: Using the method of back substitution:
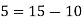
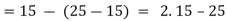

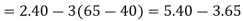
Conclusion: 65(-3) + 40(5) = 5.
Q 7: Let 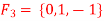 be the field of integers modulo 3, a(x) =
be the field of integers modulo 3, a(x) = 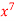 ,
,
Solution: b(x) = 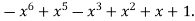 Then the behavior of Euclid’s algorithm is given in table.
Then the behavior of Euclid’s algorithm is given in table.
An Example of Euclid’s algorithm.
i |
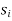 | 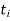 | 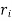 | 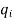 |
-1 0 1 2 3 4 5 | 1 0 1 x 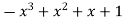 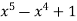 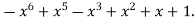 | 0 1 x+1 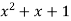 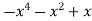 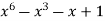 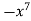 | 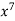 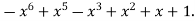 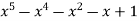 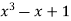 x 1 0 | - -
-x-1 -1 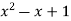 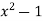 x |
Q 8: Find the prime factors of 1240.
Solution:
Steps | Prime Factors | Product |
Step 1: Divide by 2 | 2 | 1240 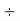 |
Step 2: Divide by 2 | 2 | 620 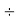 |
Step 3: Divide by 2 | 2 | 310 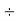 |
Step 4: Divide by 5 | 5 | 155 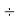 |
Step 5: Divide by 31 | 31 | 31 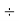 |
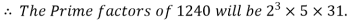
Q 9: Find the prime factors of 544:
Solution:
Steps | Prime Factors | Product |
Step 1: Divide by 2 | 2 | 544 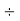 |
Step 2: Divide by 2 | 2 | 272 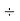 |
Step 3: Divide by 2 | 2 | 136 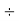 |
Step 4: Divide by 2 | 2 | 68  |
Step 5: Divide by 2 | 2 | 34 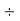 |
Step 6: Divide by 17 | 17 | 17 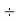 |
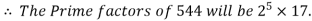
Q 10: The prototypical example of a congruence relation is congruence modulo n on the set of integers. For a given positive integer n, two integers a and b are called congruent modulo n, written

Solution:
if a-b is divisible by n (or equivalently if a and b have the same remainder when divided by n).
for example, 37 and 57 are congruent modulo 10.
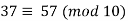
Since 37 – 57 = -20 is a multiple of 10, or equivalently since both 37 and 57 have a remainder of 7 when divided by 10. Congruence moduli n (for a fixed n) is compatible with both addition and multiplication on the integers. That is, if
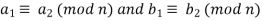
Then,
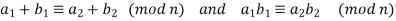
The corresponding addition and multiplication of equivalence classes is known as modular arithmetic. From the point of view of algebra, congruence modulo n is a congruence relation on the ring of integers, and arithmetic modulo n occurs on the corresponding quotient ring.
Q 11:

Remember that this means that m
Called “congruence modulo m”
Solution:
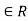
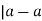
a-a = 0, which is divisible by m
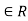
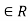
(a, b) means that m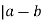
Or that km = a-b. negating that, we get b-a = -km
Thus, m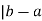 , so (b, a)
, so (b, a) 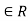
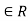
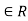
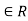
(a, b) means that m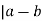 , or that km = a-b
, or that km = a-b
(b, c) means that m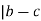 , or that lm = b-c
, or that lm = b-c
(a, c) means that m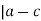 , or that nm = (a-b) + (b-c)
, or that nm = (a-b) + (b-c)
Or (k +l) m = a-c
Thus, m divides a-c, where n = k +l
Thus, congruence modulo m is an equivalence relation.
Q 12: find modulo addition of the following: 
Solution: (2 + 7) mod 5 = 9 mod 5 = 4
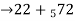
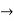 (22 + 72) mod 5 = 4
(22 + 72) mod 5 = 4
 in other way we can write as,
in other way we can write as,
22 mod 5+72 mod 5 = 2 mod 5 + 2 mod 5
= 4 mod 5 = 4.
Q 13: find modular inverse of 600
Solution: by applying Euclidean algorithm.
600 = 43.15+15
43 = 15.2+ 13
15 = 13 .1+2
13 = 2.6 +1
Then work backwards:
1 = 13 -2.6
= 13-(15-13.1)6 = 13.7 – 15.6
= (43 – 15.2)7 – 15.6 = 43.7 – 15.20
= 43.7 – (600-43. 15)20 = 43. 307 – 600.20
Finally take mod 600:
1  43.307
43.307
Thus t = 307 is an inverse.
Q 14: solve using euler’s phi-function 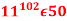
Solution: we check the given number using euler’s phi-function
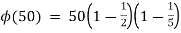
= 50*(1/2)(4/5)
= 20.
So, 
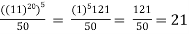
Note: 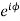 = cos
= cos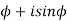
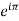 +1 = 0
+1 = 0
Q 15 Let p>5 be a prime number, and let k be any positive integer<p. Show that the decimal expansion of k/p consists of p-1 repeating decimal digits.
Solution: By Fermat’s theorem, 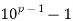 is divisible by p, say pa =
is divisible by p, say pa = 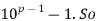
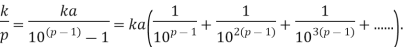
Since ka<pa<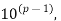 write ka as a (p-1) digit number (with 0s in the front if necessary). The above expansion shows that the (p-1) digit number will repeat.
write ka as a (p-1) digit number (with 0s in the front if necessary). The above expansion shows that the (p-1) digit number will repeat.
For example, let k = 2 and p = 7. Then a = 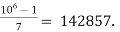 So ka = 285714. So
So ka = 285714. So