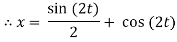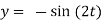Unit-1
Linear differential equations
Question-1: Solve 
Sol.
Its auxiliary equation is-
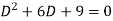
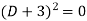
Where-
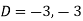
Therefore the complete solution is-
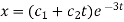
Questin-2: Solve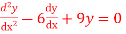
Or,
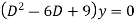
Ans. Auxiliary equation is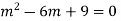
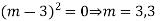
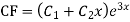
Note: If roots are in complex form i.e. 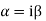
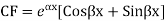
Question-3: Solve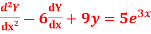
Ans. Given, 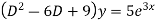
Auxiliary equation is 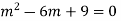
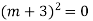
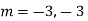
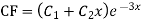
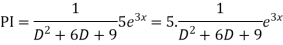
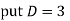
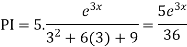
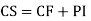
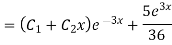
Question-4: 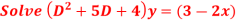
Given, 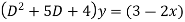
For CF,
Auxiliary equation is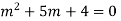
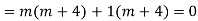
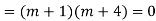

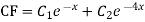
For PI
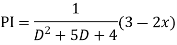
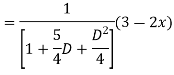
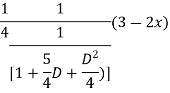
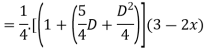
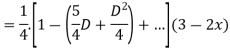



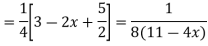
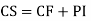
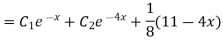
Question-5: Solve 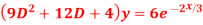
Ans. The AE is 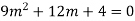

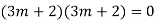
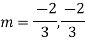

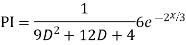
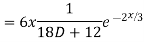
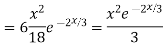
Complete solution y= CF + PI
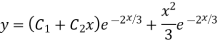
Question-6: Solve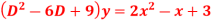
Ans. The AE is 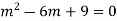
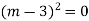
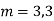
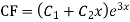
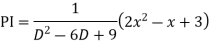
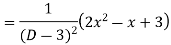
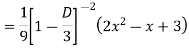
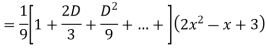
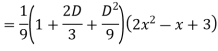
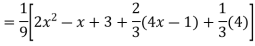
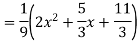
Complete solutio0n is y= CF + PI
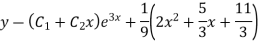
Question-7: solve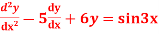
Ans. Given equation in symbolic form is
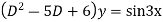
Its Auxiliary equation is 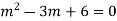
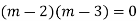
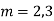
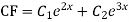
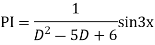
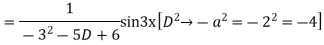
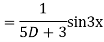
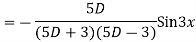
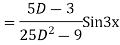
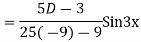

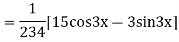
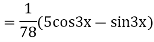
Complete solution is y= CF + PI
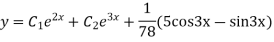
Question-8: Find the PI of(D2-4D+3)y=ex cos2x
Ans. 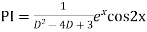
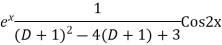
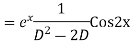
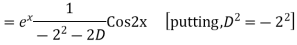
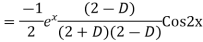
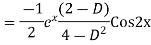
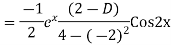
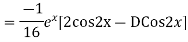
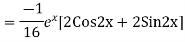
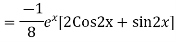
Question-9: Solve 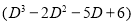
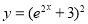
Solution:
Auxiliary equation 
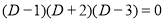
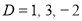
Complementary function 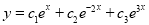

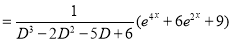
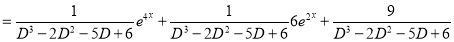


Complete Solution is 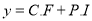
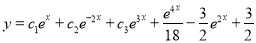
Question-10: Solve 
Solution:
The auxiliary equation is 
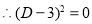
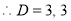
 The C.F is
The C.F is
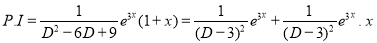

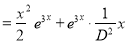
But 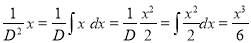
 The Complete Solution is
The Complete Solution is 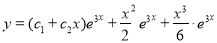
Question-11: Solve the following DE by using a variation of parameters-
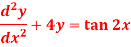
Sol. We can write the given equation in symbolic form as-
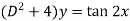
To find CF-
It’s A.E. is 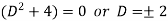
So that CF is- 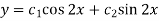
To find PI-
Here 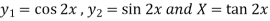
Now 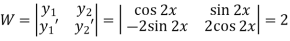
Thus PI = 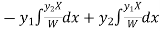
= 
= 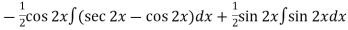
= 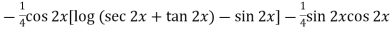
= 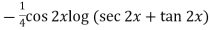
So that the complete solution is-

Question-12: Solve 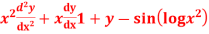
Ans. Let, 

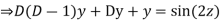
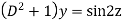
AE is 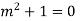
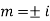
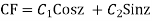

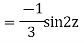
y= CF + PI
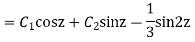
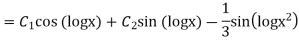
Question-13: Solve 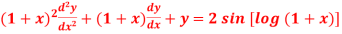
Sol. As we see that this is Legendre’s linear equation.
Now put 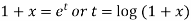
So that- 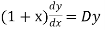
And 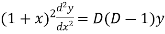
Then the equation becomes- D (D – 1)y+ Dy + y = 2 sin t
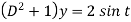
Its auxiliary equation is- 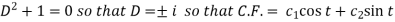
And particular integral-
P.I. = 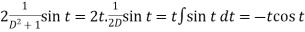
Note - 
Hence the solution is - 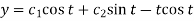
Question-14: Solve the following simultaneous differential equations-
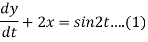
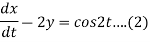
Given that x(0)=1 and y(0)= 0
Solution:
Consider the given equations,
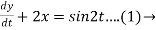 Dy +2x = sin2t
Dy +2x = sin2t
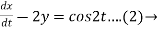 Dx -2y = cos2t
Dx -2y = cos2t
By solving the above equations we get,
(D2 +4)Y =0


X(0) = 1, y(0) = 0
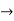 A =0, B=-1
A =0, B=-1