Unit-6
Numerical Method
Question-1: Using Newton’s divided difference formula, find the values of 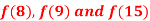 from the following table:
from the following table:
x | 4 | 5 | 7 | 10 | 11 | 13 |
f(x) | 48 | 100 | 294 | 900 | 1210 | 2028 |
Solution: We construct the divided difference table is given by:
x | f(x) | First-order divide difference | Second-order divide difference | Third-order divide difference | Fourth-order divide difference |
4
5
7
10
11
13 | 48
100
294
900
1210
2028 |
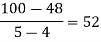
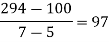

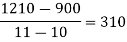
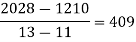 |

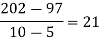
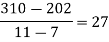
 |
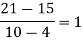
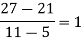
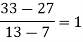 |
0
0 |
By Newton’s Divided difference formula
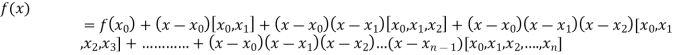 .
.
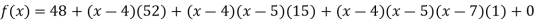
Now, putting  in above we get
in above we get
 .
.
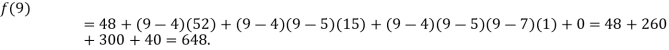
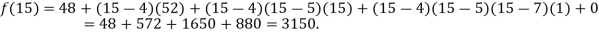
Question-2: Find a polynomial satisfied by 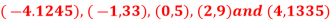 , by the use of Newton’s interpolation formula with a divided difference.
, by the use of Newton’s interpolation formula with a divided difference.
x | -4 | -1 | 0 | 2 | 4 |
F(x) | 1245 | 33 | 5 | 9 | 1335 |
Solution: Here
We will construct the divided differencetable:
x | F(x) | First-order divided difference | Second-order divided difference | Third-order divided difference | Fourth-order divided difference |
-4
-1
0
2
4 | 1245
33
5
9
1335 |
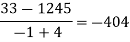
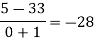
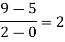

|
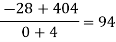
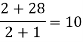
 |
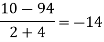
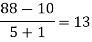 |
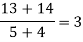 |
By Newton’s divided difference formula
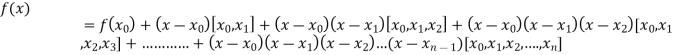 .
.
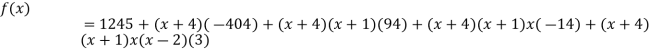

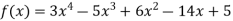
This is the required polynomial.
Question-3: Given  find
find , by usingNewton forwardinterpolationmethod.
, by usingNewton forwardinterpolationmethod.
Solution: Let , then
, then
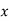 | 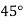 | 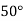 |  | 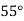 | 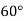 |
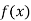 | 0.7071 | 0.7660 | - | 0.8192 | 0.8660 |
The table of forward finite difference is given below:
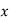 | 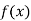 | 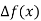 | 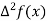 | 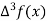 |
45
50
55
60 | 0.7071
0.7660
0.8192
0.8660 |
0.0589
0.0532
0.0468 |
-0.0057
-0.0064 |
-0.0007 |
By Newton forward difference method
Here initial value 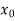 = 45, difference ofintervalh = 5 andthe value to be calculated at x=52.
= 45, difference ofintervalh = 5 andthe value to be calculated at x=52.

By Formula

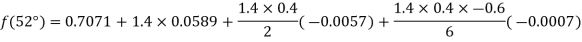

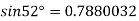
Question-4: Find the missing term in the following:
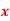 | 0 | 1 | 2 | 3 | 4 |
 | 1 | 3 | 9 | ? | 81 |
Solution: Let 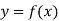
First, we construct the forward difference table:
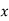 | 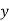 | 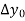 | 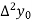 |  |
0
1
2
3
4 | 1
3
9
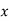
81 |
2
6
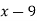
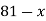 |
4
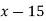
 |

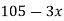 |
Now, 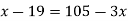


Question-5: The following table gives the amount of a chemical dissolved in water:
Temp. |  |  |  |  |  |  |
Solubility | 19.97 | 21.51 | 22.47 | 23.52 | 24.65 | 25.89 |
Solution: Compute the amount dissolve at 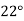
Consider the following backward difference table:
Temp.x | Solubility y | 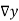 | 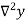 |  | 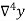 | 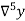 |
10
15
20
25
30
35 | 19.97
21.51
22.47
23.52
24.65
25.89 |
1.54
0.96
1.05
1.13
1.24 |
-0.58
0.09
0.08
0.11 |
0.67
-0.01
0.03 |
-0.68
0.04 |
0.72 |
Here 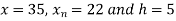

By Newton Backward difference formula
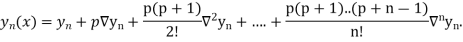

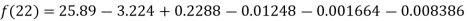
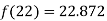
Question-6: Use the inverse Lagrange’s method to find the root of the equation 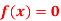 , give data
, give data 
X | 30 | 34 | 38 | 42 |
F(x) | -30 | -13 | 3 | 18 |
Solution: Here 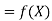 , we have thedata
, we have thedata
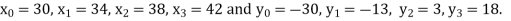
Also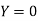 .
.
Lagrange’s inverse interpolation formula is given by
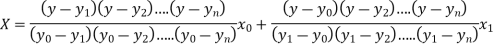
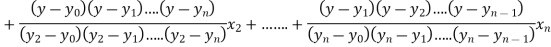
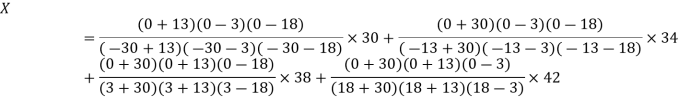

Thus the approximate root of the given equation is 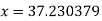 .
.
Question-7: Given that
X | 1.0 | 1.1 | 1.2 | 1.3 |
Y | 0.841 | 0.891 | 0.932 | 0.963 |
Find  at
at 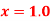 .
.
Solution: Here the first derivative is to be calculated at the beginning of the table, therefore forward difference formula will be used
Forward difference table is given below:
X | Y |  |  | 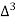 |
1.0
1.1
1.2
1.3 | 0.841
0.891
0.932
0.962 |
0.050
0.041
0.031 |
-0.009
-0.010 |
-0.001 |
By Newton’s forward differentiation formula for differentiation
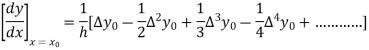
Here

Question-8: From the following table of values of x and y find 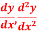 for
for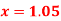
X | 1.00 | 1.05 | 1.10 | 1.15 | 1.20 | 1.25 | 1.30 |
Y | 1.0000 | 1.02470 | 1.04881 | 1.07238 | 1.09544 | 1.11803 | 1.14017 |
Here the value of the derivative is to be calculated at the beginning of the table.
Solution: Forward difference table is given by
X | Y | 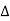 | 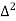 | 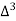 | 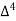 | 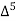 |  |
1.00
1.05
1.10
1.15
1.20
1.25
1.30 | 1.0000
1.02470
1.04881
1.07238
1.09544
1.11803
1.14017 |
0.02470
0.02411
0.02357
0.02306
0.02259
0.02214 |
-0.00059
-0.00054
-0.00051
-0.00047
-0.00045 |
0.00005
0.00003
0.00004
0.00002 |
-0.00002
0.00001
-0.00002 |
0.00003
-0.00003 |
-0.00006 |
From Newton’s forward difference formula for differentiation we get

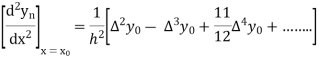
Here 

=0.48763
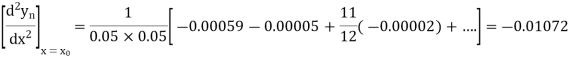
Question-9: Given that
X | 0.1 | 0.2 | 0.3 | 0..4 |
Y | 1.10517 | 1.22140 | 1.34986 | 1.49182 |
Find 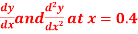 ?
?
Solution: Backward difference table:
X | Y |  |  | 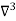 |
0.1
0.2
0.3
0.4 | 1.10517
1.22140
1.34986
1.49182 |
0.11623
0.12846
0.14196 |
0.01223
0.01350 |
0.00127 |
Newton’s Backward formula for differentiation
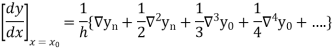

Here 

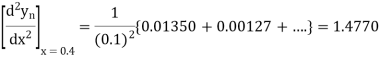
Question-10: State the trapezoidal rule for finding an approximate area under the given curve. A curve is given by the points (x, y) given below:

Estimate the area bounded by the curve, the x-axis, and the extreme ordinates.
Solution: We construct the data table:
X | 0 | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
Y | 23 | 19 | 14 | 11 | 12.5 | 16 | 19 | 20 | 20 |
Here length of interval h =0.5, initial value a = 0 and final value b = 4
By Trapezoidal method
Area of curve bounded on x-axis =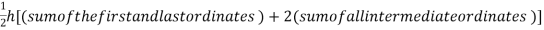
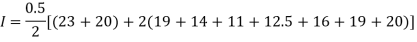
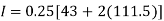
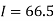
Question-11: Evaluate, using trapezoidal rule with five ordinates
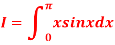
Here 
Solution: We construct the data table:
X | 0 |  |  |  | 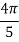 | 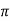 |
Y | 0 | 0.3693161 | 1.195328 | 1.7926992 | 1.477265 | 0 |
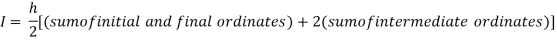
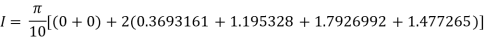
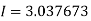
Question-12: Evaluate
Solution: Let us divide the range of the interval [0,6] into six equal parts.
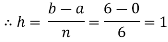
For h=1, we construct the data table:
X | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
 | 1 | 0.5 | 0.2 | 0.1 | 0.0588 | 0.0385 | 0.027 |
By Simpson’s 3/8 rule
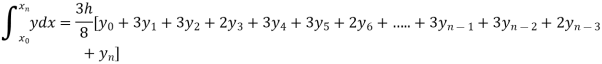
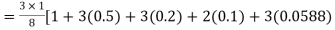 +3(0.0385)+0.027]
+3(0.0385)+0.027]
=1.3571
Question-13: Using Euler’s method solves the differential equation for y at x=1 in five steps
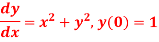
Solution: Given equation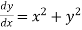
Here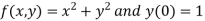
No. of steps n=5 and so that 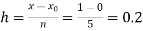
So that 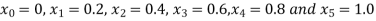
Also 
By Euler’s formula
 , n=0,1,2,3,4 ……(i)
, n=0,1,2,3,4 ……(i)
For n=0 in equation (i) we get
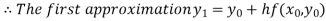
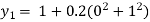

For n=1in equation (i) we get
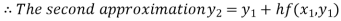

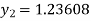
For n=2in equation (i) we get

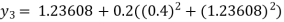
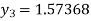
For n=3in equation (i) weget



For n=4in equation (i) weget
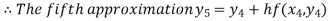
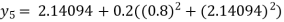

Hence
Question-14: Using modified Euler’s method, obtain a solution of the equation
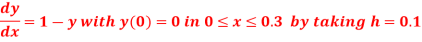
Solution: Given equation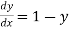
Here 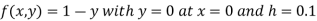
By modified Euler’s formula, the initial iteration is
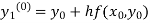
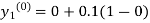
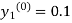
The iteration formula by modified Euler’s method is
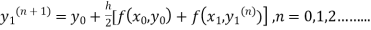 -----(i)
-----(i)
For n=0in equation(i)we get
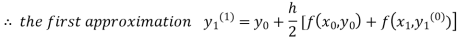
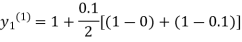
Where  and
and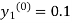 asabove
asabove
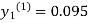
For n=1in equation(i)we get

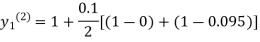

For n=2 in equation(i)we get
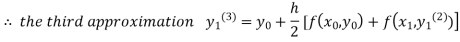
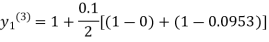

For n=3in equation(i)we get
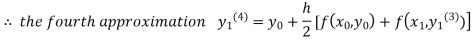
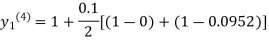

Since the third and fourth approximation is equal.
Hence y=0.0952 at x=0.1
To calculate the value of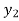 at x=0.2
at x=0.2
By modified Euler’s formula, the initial iteration is
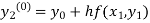
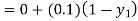
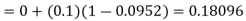
The iteration formula by modified Euler’s method is
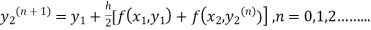 -----(ii)
-----(ii)
For n=0in equation(ii)we get
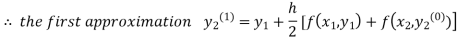

 1814
1814
For n=1in equation(ii)we get
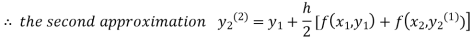
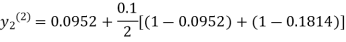
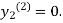 1814
1814
Since the first and second approximations are equal.
Hence y= 0.1814atx=0.2
To calculate the value of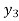 at x=0.3
at x=0.3
By modified Euler’s formula, the initial iteration is
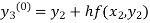
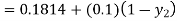
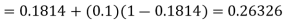
The iteration formula by modified Euler’s method is
 -----(iii)
-----(iii)
For n=0in equation(iii)we get
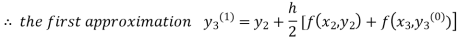
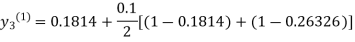
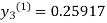
For n=1in equation(iii)we get
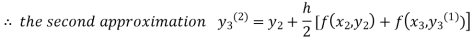
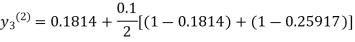

For n=2 in equation(iii)we get
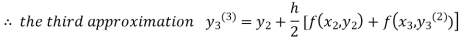
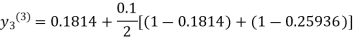
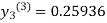
For n=3 in equation(iii)we get


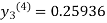
Since the third and fourth approximations are the same.
Hence y= 0.25936 at x = 0.3
Question-15: Apply Runge-Kutta fourth-order method to find an approximate value of y for x=0.2 in the step of 0.1,if

Solution: Given equation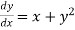
Here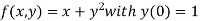
Also 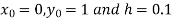
By Runge-Kutta formula for first interval
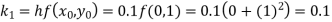
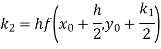

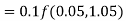
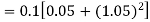
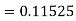
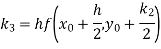
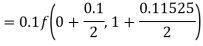
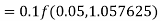
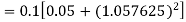
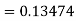

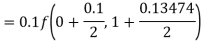
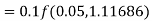

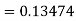
A fourth order Runge-Kutta formula:


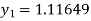
Again 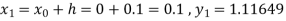
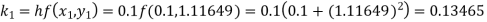
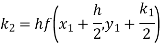
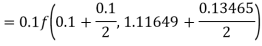
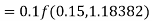

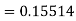


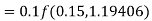

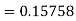
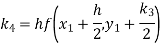
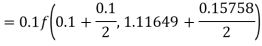

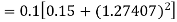
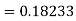
A fourth order Runge-Kutta formula:
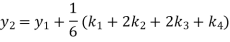
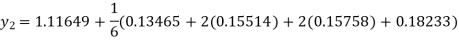
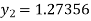
Question-16: Using Runge Kutta method of order four, solve  to find
to find 
Solution: Given Second-order differential equation is

Let 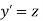 then above equation reduces to
then above equation reduces to
Or 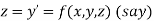
 (say)
(say)
Or 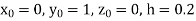 .
.
By Runge Kutta Method we have
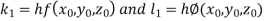
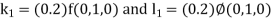
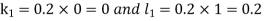
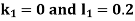
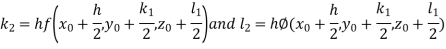
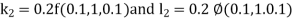
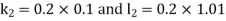
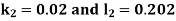
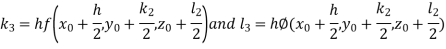
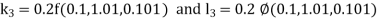
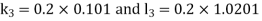
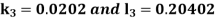

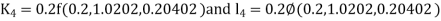
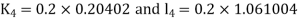
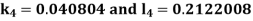
A fourth order Runge Kutta formula:

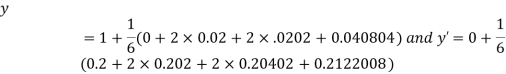
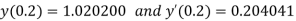
Question-17: Solve the differential equations
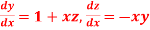 for
for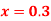
Using the four order Runge Kutta method with initial conditions 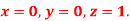
Solution: Given differential equation are
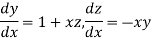
Let 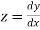
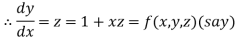
And 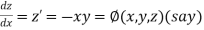
Also 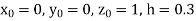
By Runge Kutta Method we have
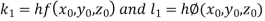
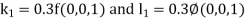

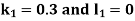

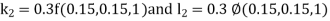
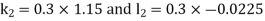
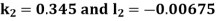
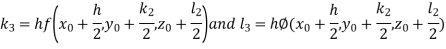
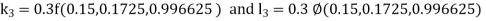
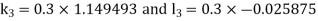
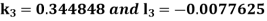

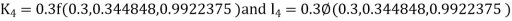
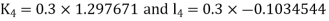

A fourth order Runge Kutta formula:
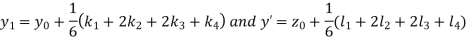

And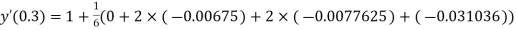
 .
.