Unit 1
Q1) Represent -45 in 2’s compliment form?
Sol: Firstly finding 1’s compliment of +45 and then adding 1 to it
+45 = 00101101
1’s compliment = 11010010
2’s compliment = 1’s compliment +1
= 11010010+1
= 11010011
Q2) Subtract 14 from 46 using 8-bit 2’s compliment?
Sol: We need to find the 2’s compliment of subtrahend i.e -14 and add it to the minuend i.e 46.
1’s compliment of +14 = 11110001
2’s compliment of -14 = 1’s compliment of +14 +1
= 11110010
46-14 = 00101110-11110010
= 00100000 (ignore carry)
Q3) Add -75 and +26 using 8-bit 2’s compliment?
Sol: +75= 01001011
-75= 10110101 (2’s compliment)
+26 = 00011010
 -75 = 10110101
-75 = 10110101
11001111
As we have no carry and the MSB is 1 so the result is a negative number and is in 2’s compliment form of 11001111 is 00110001 = 49.
Answer = -49
Q4) Convert the Boolean function into Standard PoS form.
f = (p + q + r).(p + q + r’).(p + q’ + r).(p’ + q + r)
Sol: Step 1 – By using the Boolean postulate, x.x = x and writing the first term p+q+r two more times we get
⇒ f = (p + q + r).(p + q + r).(p + q + r).(p + q + r’).(p +q’ + r).(p’ + q + r)
Step 2 – Now by using Distributive law, x + (y.z) = (x + y).(x + z) for 1st and 4thparenthesis, 2nd and 5th parenthesis, 3rd and 6th parenthesis.
⇒ f = (p + q + rr’).(p + r + qq’).(q + r + pp’)
Step 3 − Applying Boolean postulate, x.x’=0 for simplifying of the terms present in each parenthesis.
⇒ f = (p + q + 0).(p + r + 0).(q + r + 0)
Step 4 − Using Boolean postulate, x + 0 = x we get
⇒ f = (p + q).(p + r).(q + r)
⇒ f = (p + q).(q + r).(p + r)
This is the simplified Boolean function.
Q5) For f(A,B,C) = A+B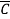 +AB
+AB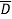 +ABCD. Find min terms?
+ABCD. Find min terms?
Sol: f(A,B,C) = A(B+ 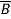 )(C+
)(C+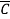 )(D+
)(D+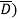 +BC(A+
+BC(A+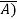 (D+
(D+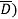 +AB
+AB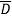 ((C+
((C+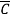 )+ABCD
)+ABCD
=ABCD+ABC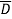 +AB
+AB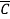 D+AB
D+AB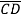 +A
+A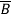 CD+A
CD+A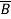 C
C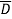 +A
+A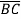 D+A
D+A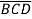 +
+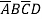 +
+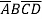
=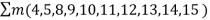
Q6) Convert the Boolean function into Standard SoP form f = p’qr + pq’r + pqr’ + pqr
Sol: Step 1 – By using the Boolean postulate, x + x = x and also writing the last term pqr two more times we get
⇒ f = p’qr + pq’r + pqr’ + pqr + pqr + pqr
Step 2 – By Using Distributive law for 1st and 4th terms, 2nd and 5th terms, 3rdand 6th terms.
⇒ f = qr(p’ + p) + pr(q’ + q) + pq(r’ + r)
Step 3 – Then Using Boolean postulate, x + x’ = 1 we get
⇒ f = qr(1) + pr(1) + pq(1)
Step 4 – hence using Boolean postulate, x.1 = x we get
⇒ f = qr + pr + pq
⇒ f = pq + qr + pr
This is the required Boolean function.
Q7) Simplify f(X,Y,Z)=∏M(0,1,2,4)f(X,Y,Z)=∏M(0,1,2,4)using K-map.
Sol: 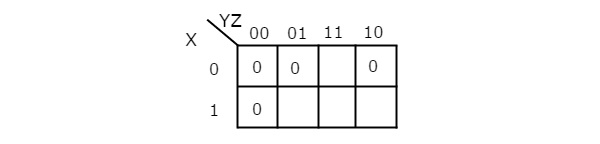
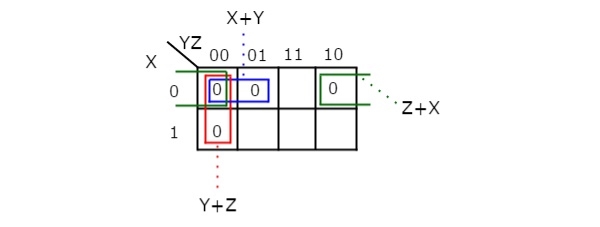
Therefore, the simplified Boolean function is
f = (X + Y).(Y + Z).(Z + X)
Q8) Simplify F(P,Q,R,S)=∑(0,2,5,7,8,10,13,15)
Sol:
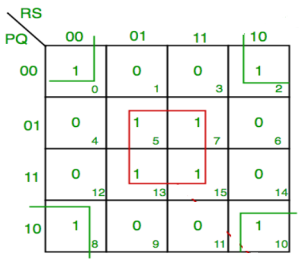
F = P’Q’R’S’ + PQ’R’S’ + P’Q’RS’ +PQ’RS’ + QS
F = P’Q’S’ + PQ’S’ + QS
F = Q’S’ +QS
Q9) Simplify: F(A,B,C)=π(0,3,6,7)
Sol:

F = A’BC +ABC +A’B’C’ +ABC’
F = BC + C’ ( A’B’ + AB )
Q10) What are BCD and Binary codes explain in detail?
- Sol: Binary Coded Decimal (BCD) code
- Here each decimal digit is represented by a 4-bit binary number.
- It's a way to express each of the decimal digits with a binary code.
- Therefore, by four bits we can represent sixteen numbers (0000 to 1111).
- But in BCD code only the first ten of these numbers are used (0000 to 1001) and rest are invalid.

Fig.3: BCD codes (Ref. 1)
Advantages of BCD Codes
- It is very similar to the decimal system.
- We have to remember the binary equivalent of 0 to 9 only.
Disadvantages of BCD Codes
- The addition and subtraction of the BCD number system have different rules.
- The BCD arithmetic is more complicated.
- BCD code requires more number of bits than binary code to represent the decimal number.
- Hence is less efficient than binary.
2. Binary Code
- In coding, when alpha-numeric characters or words are represented by a specific group of symbols, it is said that it is being coded.
- The group of symbols is known as a code.
- The digital data can be represented, stored, and transmitted as a group of binary bits.
- This group is called a binary code.
- It is represented by the number as well as the alphanumeric character.
Advantages of Binary Code
- They are used in computer applications.
- They are suitable for digital communications.
- They make the analysis and designing of digital circuits easy.
- Implementation becomes very easy since only 0 & 1 are being used.
Q11) Explain in detail the working of CMOS NAND gate?
Sol: The CMOS NAND Gate is shown below. It has two transistors Q1 and Q3 connected in series and having the same input A. The transistor Q1 is turned ON when the input is high and the transistor Q3 is turned OFF during that period and viceversa.
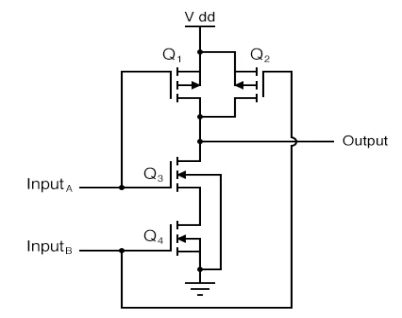
Fig: CMOS NAND Gate
The transistors Q2 and Q4 are connected in series having same input B. The transistors Q1 and Q2 have their source and drain connected in parallel. So, when any of the transistor amongst the two saturates the output goes HIGH. The transistors Q3 and Q4 have their source and drain connected in series. When both these transistors saturate the output goes LOW.
Q12) Make a K-map of the following expression and obtain minimal expression in SOP and POS form F=AB+A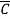 +C+AD+A
+C+AD+A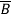 C+ABC
C+ABC
Sol: In SOP Form: F= 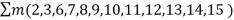
In POS Form: F= 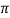 M (0,1,4,5)
M (0,1,4,5)
SOP Minimal
 AB CD
AB CD
|
| 1 | 1 |
|
| 1 | 1 |
1 | 1 | 1 | 1 |
1 | 1 | 1 | 1 |
Fmin= A+C
POS minimal
 AB CD
AB CD
0 | 0 |
|
|
0 | 0 |
|
|
|
|
|
|
|
|
|
|
Fmin= A+C
Q13) For an n-variable Boolean function, the maximum number of prime implicants will be?
Sol: 2(n-1)