Unit 3

CONTEXT FREE GRAMMAR AND LANGUAGES

1. Define phase structure grammar.
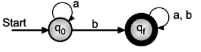
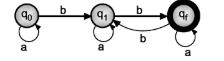
2. Construct regular grammar for FA shown in figure.

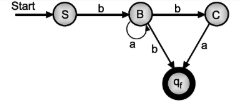
3.     Convert the following right linear grammar to equivalent left linear grammar.

SbB

BbC |aB|b

4.     State that a derivation tree is a natural description of the derivation of a particular sentential form of the grammar G.

5.     Let G= {{S} {a,b+ ,*},P,S} where P= {S S|S*S|a|b| .

6.     Compute generating symbols:

G={{S,A},{a,b},{SAB|a,A  b},S}

7.     Write and explain algorithm for testing.

8.     Consider G with P= {Sas|AB

     Aꞓ

    Bꞓ

    D b }

         Construct G’ generating L(G) –{ꞓ}.

9.     Give a grammar generating the strings of language L.

L = {anban |n≥1}

10. Write the CFG for given CFL’s.