undefined | unit 1 spur gear

Back to Study material

TOM2

Unit 1

Spur Gear

Q1) Classify gears.

Ans.

According to the position of axes of the shafts.

Parallel

The two parallel and coplanar shafts connected by the gears are shown in Fig.

These gears are called spur gears and the arrangement is known as spur gearing.

These gears have teeth parallel to the axis of the wheel as shown in the figure.

Another name given to the sperm gearing is helical gearing, in which the teeth are inclined to the axis. the single and double helical gears connecting parallel shafts as shown in figure (a) and (b) respectively.

b. Intersecting

The two non-parallel or intersecting, but coplanar shafts connected by gears are shown in figure c.

These gears are called bevel gears and the arrangement is known as bevel gearing.

c. Non-intersecting and non-parallel

The two non-intersecting and non-parallel shaft connected by gears is shown in a figure these gears are called skew bevel gears or spiral gears and the arrangement is known as skew bevel gearing or spiral gearing.

2. According to the type of gearing.

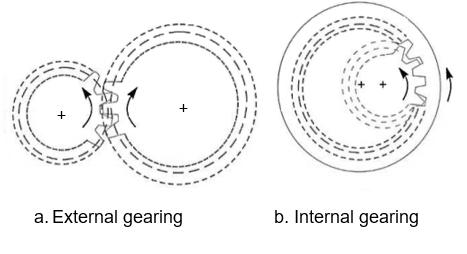
d. External gearing

In external gearing, the gears of the two shafts mesh externally with each other as shown in figure a.

The larger of these two wheels is called spur wheel and the smaller wheel is called the pinion.

e. Internal gearing

In internal gearing, the gears of the two shafts mesh internally with each other as shown in figure b.

The larger of these two wheels is called the annular wheel and the smaller wheel is called the pinion.

f. Rack and pinion

Sometimes, the gear of a shaft meshes externally and internally with the gears in a straight line, as shown in the figure such type of gear is called rack and pinion.

The straight-line gear is called rack and the circular wheel is called the pinion.

3. According to the position of teeth on the gear surface

g. Straight

h. Inclined

i. Curved.

Q2) Define spur gear.

Ans.

When the teeth of the gear are parallel to the axis of the wheel the gears are called spur gears and the arrangement is known as spur gearing.

They consist of a cylinder or disk with teeth projecting radially.

Spur gears or straight-cut gears are the simplest types of gear.

Q3) Define pitch circle, pressure angle, addendum, dedendum.

Ans.

Pitch Circle:- It is an imaginary circle which by the pure rolling action, would give the same motion as the actual gear.

Pressure angle or angle of obliquity. It is the angle between the common normal to two gear teeth at the point of contact and the common tangent at the pitch point. It is usually denoted by

. The standard pressure angles are 14.5° and 20°

Addendum:- It is the radial distance of a tooth from the pitch circle to the top of the tooth.

Dedendum:- It is the radial distance of a tooth from the pitch circle to the bottom of the tooth.

2. Define diametral pitch, module, circular pitch, face width.

Ans.

Diametral pitch:- It is the ratio of a number of teeth to the pitch circle diameter in millimeters.

It is denoted by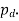

Mathematically,

Diametral pitch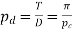

T=number of teeth

D=pitch circle diameter

Module:- It is the ratio of the pitch circle diameter in millimeters to the number of teeth. It is usually denoted by m. Mathematically,

Module m=D/T

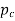
Circular pitch:- It is the distance measured on the circumference of the pitch circle from a point of one tooth to the corresponding point on the next tooth. It is usually denoted by

Mathematically,

Circular pitch.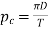

D=diameter of the pitch Circle, and

T= number of teeth on the wheel

Face width:- It is the width of the gear tooth measured parallel to its axis.

Q4) Differentiate between involute & cycloidal teeth.

Ans

Sr No.	Cycloidal teeth	Involute teeth
1	Pressure angle varies from a maximum at the beginning of the engagement, reduces to zero at the pitch, and again increases to a maximum at the end of engagement resulting in the less smooth running of the gears.	The pressure angle is constant throughout the engagement of teeth. This results in the smooth running of the gears.
2	It involves a double curve for the teeth, epicycloid, and hypocycloid. This complicates the manufacture.	It involves a single curve for the teeth resulting simplicity of manufacturing and tools.
3	Owing to the difficulty of manufacture these are costlier	These are simple to manufacture and thus cheaper.
4	Exact center distance is required to transmit a constant velocity ratio	A little variation in the center distance does not affect the velocity ratio
5	The phenomenon of interference does not occur at all	Interference can occur if the condition of a minimum number of teeth on a gear is not followed
6	The teeth have spreading flanks and thus are stronger	The teeth have radial flanks and thus are weaker as compared to the cycloidal form for the same pitch.
7	In this, convex flank always has contact with a concave face resulting in less wear	Two convex surfaces are in contact and do there is more wear.

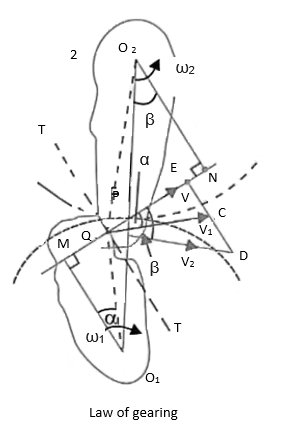
Q5) Explain the law of gearing.

Ans.

Consider the portions of the two teeth, one on the wheel 1 and the other on the wheel 2 as shown by the thick line curves in the figure.

Let the two teeth come in contact at point Q, and the wheels rotate in the directions as shown in the figure.

Let T T be the common tangent and MN be the normal curves at the point of contact Q.

From the centers

draw

perpendicular to MN .

A little consideration will show that the point Q moves in the direction QC when considered as a point on wheel 1 and in the direction QD when considered as a point on wheel 2.

Let

be the velocities of the point Q on the wheels 1 and 2 respectively.

If the teeth are to remain in contact, then the components of these velocities along the common normal MN must be equal.

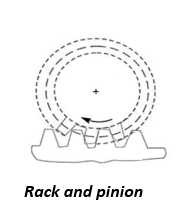
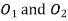
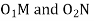
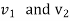
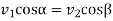
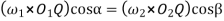
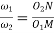………. I

Also, from similar triangles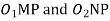

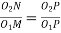……….. II

Combining equations, I and II we have

From above, we see that the angular velocity ratio is inversely proportional to the ratio of the distances of the point P from the centers

or the common normal to the two surfaces at the point of contact Q intersects the line of centers at point P which divides the center distance inversely as the ratio of angular velocities.

Therefore, to have a constant angular velocity ratio for all positions of the wheels, the point P must be the fixed point for the two wheels.

In other words, the common normal at the point of contact between a pair of teeth must always pass through the pitch point.

This is the fundamental condition that must be satisfied while designing the profiles for the teeth of gear wheels.

It is also known as the law of gearing.

Q6) Derive an expression for the path of contact & arc of contact.

Ans.

Consider a pinion driving the wheel as shown in the figure.

When the pinion rotates in the clockwise direction, the contact between a pair of involute teeth begins at K and ends at L.

MN is the common normal at the point of contact and the common tangent to the base circles.

Point K is the intersection of the addendum circle of the wheel and the common tangent.

The point L is the intersection of the addendum circle of pinion and common tangent.

We know that the length of the path of contact is the length of common normal cut off by the addendum circles of the wheel and the pinion.

Thus the length of the path of contact is KL which is the sum of the parts of the path of contacts KP and PL.

The part of the path of contact KP is known as the path of approach and the part of the path of contact PL is known as the path of recess.

Let. radius of the addendum circle of the pinion.

radius of the addendum circle of the wheel.

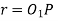= radius of pitch Circle of pinion, and

radius of pitch Circle of the wheel.

From the figure, we find that radius of the base circle of pinion

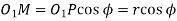
And the radius of the base circle of the wheel,

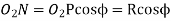
Now from right angle triangle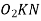

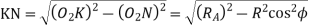
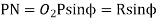
Length of the part of the path of contact, or the path of approach,

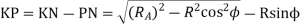
Similarly from right-angled triangle

And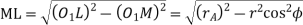

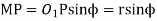
Length of the part of the path of contact, or the path of recess

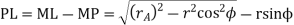
Length of the path of contact,

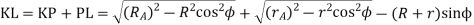
Arc of contact

The arc of contact is the path traced by a point on the pitch circle from the beginning to the end of the engagement of a given pair of teeth.

In figure arc of contact is EPH or GPH.

Considering the arc of contact GPH, it is divided into two parts arc GP and arc PH.

The arc GP is known as arc of approach and the arc PH is called arc of recess.

The angles subtended by these arcs at

are called the angle of approach and angle of recess respectively.

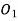
We know that the angle of the arc of approach

And the length of the arc of recess

Since the length of the arc of contact GPH is equal to the sum of the length of the arc of approach and arc of recess, therefore,

Length of the arc of contact

Q7) Explain conjugate action in gears.

Ans

The gears must be designed such that the ratio of rotational speeds of driver and driver gear is always constant.

When the tooth profiles of two meshing gear produce a constant angular velocity during meshing, they are said to be executed and conjugate action point that is

Where 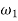=Angular velocity of the driver.

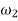=Angular velocity of the driven

Gears are mostly designed to produce conjugate action.

Theoretically, it is possible to select an arbitrary profile for one tooth and then to find a profile for the meshing tooth, which will give conjugate action.

One of these solutions is the involute profile.

The involute profile is universally used for constructing gear teeth with few expectations.

The figure illustrates a conjugate action.

There are two arms A and B with curved surfaces.

When A pushes against B the point of contact between them occurs at C, where the two contacting surfaces are tangent to each other.

The forces at any instant are directed along the common normal ‘ab’ to the two curved surfaces.

The line ab is called the line of action.

The line of action intersects the line of centers of the two curved surfaces at a point P, referred to as pitch point.

The angular velocity ratio between the two arms is equal to the ratio of their radii to point P.

Circles are drawn through the pitch point P with centers at

are called pitch circles.

The radii

are pitch radii.

To transmit constant angular velocity to B, for a given angular velocity of arms A, the pitch point P, must remain fixed.

It means that all the lines of action must pass through the same point P at all instants.

In the case of an involute profile, all points of contact occur on the same straight line ab.

That is normal to the contacting surfaces.

Thus, these profiles transmit constant angular motion.

Pitch line velocity

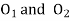
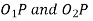
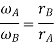
Q8) Explain interference in gears with neat sketch.

Ans.

The figure shows a pinion with the centre

in mesh with wheel or gear with center

MN is the common tangent to the base circles & KL is the path of contact between the two mating teeth.

That is the radius of the addendum circle of the pinion is increased to

, the point of contact L will move from L to N.

When this radius is further increased, the point of contact L will be on the inside of the base circle of the wheel and not on the involute profile of the tooth on the wheel.

The tip of the tooth on the pinion will then undercut the tooth on the wheel at the root and remove part of the involute profile of tooth on The wheel.

This effect is known as interference and occurs when the teeth are being cut.

The phenomenon when the tip of tooth undercuts the root on its matting gear is known as interference.

Similarly, if the radius of the addendum circle of the wheel increases beyond

then the tip of the tooth on the wheel will cause interference with the tooth on pinion.

The points M and N are called interference points.

Interference may be avoided if the path of contact does not extend beyond interference points.

The limiting value of the radius of the addendum circle of the pinion is

and of the wheel is

So, we can conclude that the interference may only be avoided if the point of contact between the two teeth is always on the involute profiles of both the teeth.

In other words, interference may only be prevented, if addendum circles of the two mating gears cut the common tangent to the base circles between the points of tangency.

When interference is just avoided, the maximum length of the path of contact is MN when the maximum addendum circles for pinion and wheel pass through the points of tangency N and M respectively as shown in the figure in such a case,

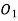
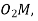
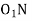
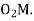
The maximum length of the path of approach,

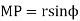
And the maximum length of the path of recess,

The maximum length of the path of contact

The maximum length of the Arc of contact

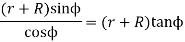
Q9) Explain different methods to avoid interference.

Ans.

In general, there are three different ways of reducing or eliminating interference and subsequent undercutting at the flank region, when a pinion has less than a minimum number of teeth to avoid interference.

By using a modified involute or composite system

When is standard addendum is used for involute pinion with the pressure angle of

° the smallest pinion that will gear with a rack without interference has 32 teeth.

In many situations, it becomes obligatory to use pinion which has 12 teeth only.

In such cases, the shape of the basic rack tooth may be modified.

The flank portion of the pinion tooth lying inside the base circle and the matting portion of the gear tooth face may be made cycloidal in place of involute shape.

The remaining portion of the pinion tooth maybe of involute profile.

2. By modifying addendum of gear tooth

To avoid interference, it is required to chop off the interfering portion of the face of the gear tooth. This is illustrated in the figure.

The resulting tooth is called stub tooth instead of full depth tooth.

As can be seen in the figure, portion A'B' of gear tooth measures with a non-involute portion in the flank of pinion tooth. If portion AA' B'B of the gear tooth is chopped off, interference will be eliminated.

However, this step amounts to reducing the radius of the addendum circle of gear, which now cuts the line of action at point K' instead of K.

In other words, the length of the path and approach and hence, the contact ratio is reduced.

3. Increased center distance

When centers

of two mating gears are slightly moved apart, the common tangent to the base circles cut the line of centers at point P'.

then become the pitch Circle radii of the mating gears.

The center distance between two involute gears may be increased within limits, without disturbing the correctness of gearing, and the step will prevent the tip of gear tooth from mating with a non-involute flank portion of the pinion, at least to some extent.

There are however two adverse consequences:

Actual pitch circle diameter is increased, this tends to reduce effective addenda and hence the arc of contact too.

As the difference in tooth space width and tooth thickness at new pitch Circle is further increased, the considerable backlash will be introduced between the teeth.

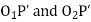
Q10) Explain undercutting with a neat sketch.

Ans.

Undercutting

The figure shows a pinion.

A portion of its dedendum falls inside the base circle.

The profile of the tooth inside the base circle is radial.

If the addendum of the mating gear is more than the limiting value, it interferes with the dedendum of the pinion, and the two gears are locked.

However, if a cutting rack having similar teeth is used to cut the teeth in the pinion, it will remove that portion of the pinion tooth which would have interfered with the gear as shown in the figure.

A gear having its material removed in this manner is set to undercut and the process undercutting.

In pinion with a small number of teeth, this can seriously weaken the tooth, however, when the actual gear meshes with the undercut pinion no interference occurs.

Undercutting will not take place if the teeth are designed to avoid interference.

Q11) Derive an expression for the minimum number of teeth on the pinion to avoid interference.

Ans.

To avoid interference, the addendum circles for the two mating gears must cut the common tangent to the base circles between the points of tangency.

The limiting condition reaches when the addendum circles of pinion and wheel pass-through point N and M respectively.

Let. t= the number of teeth on the pinion.

T= number of teeth on the wheel

m = module of the teeth

r= pitch Circle radius of pinion =m.t/2

G= Gear ratio =T/t =R/r

= Pressure angle or angle of obliquity

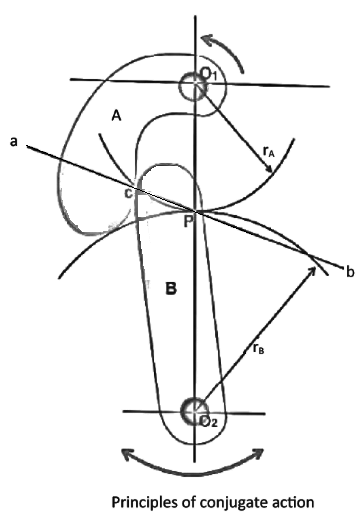
From triangle

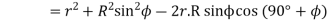
Where

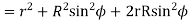
Limiting the radius of the pinion addendum circle,

Let 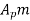= addendum of the pinion, where 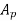is a fraction by which the standard addendum of one module for the pinion should be multiplied to avoid interference.

We know that the addendum of the pinion.

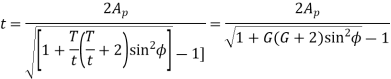
This equation gives the minimum number of teeth required on the pinion to avoid interference.

Q12) Derive an expression for a minimum number of teeth on gear to avoid interference.

Ans.

Let. T= minimum number of teeth required on the wheel to interference,

.m= addendum of the wheel, where is a fraction by which the standard addendum for the wheel should be multiplied.

Using the same notations as in the above article we have from triangle

Where

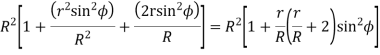
Limiting the radius of wheel addendum circle

We know that addendum of the wheel

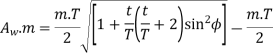
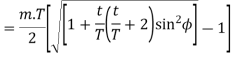
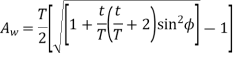
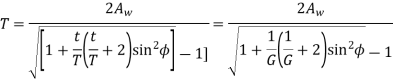
Q13) Explain gear friction & its remedies.

Ans.

Friction refers to the resistance of one substance moving against the other.

By definition, gears move against each other, and therefore experience friction to various degrees.

Gear friction occurs at the interface of lubricated tooth contacts that are subject to combined sliding and rolling motions.

Engineered gear tooth surfaces that are not smooth experience diverse lubrication conditions, ranging from full film to mixed elastohydrodynamic lubrication (EHL) or boundary lubrication conditions, depending on surface and operating conditions and lubricant characteristics.

In cases where asperity contacts occur, gear friction is defined by a combination of fluid viscous shear, rolling resistance, and dry friction at the contact interfaces.

A fundamental understanding of gear friction is essential as it impacts

(1) gear scuffing failures due to excessive heat generation and gear contact fatigue lives and associated failure modes of spalling and micro-pitting

(2) load-dependent (mechanical) gear mesh power losses, and

(3) a class of gear vibrations along the direction of the relative sliding and the damping effects along the line of action.

The following methods are used to reduce gear friction.

Different gear structures.

We can reduce the amount of friction generated by a gear set by introducing different shapes.

Helical gears, for example, experience friction gradually and distributed along the length of their teeth, making them capable of handling higher levels of friction with no problem.

2. Lower speeds and loads.

Most friction problems only arise in certain conditions—usually, when gears are operating at high speeds, or with high loads that increase the amount of friction present.

Working to lower those speeds and lows can make the friction problem disappear.

3. Lubrication.

Lubrication is one of the simplest ways to address friction.

It instantly reduces the friction between gears but must be reapplied occasionally to keep parts moving.

4. Material selection.

We can also produce gears out of special materials that do not experience as much friction as their counterparts, such as certain metal alloys.

Sign Up