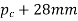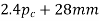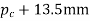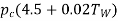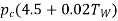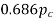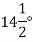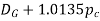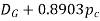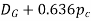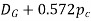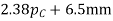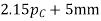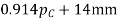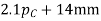undefined | unit 2 helical bevel worm and worm wheel

TOM2

Unit II

Helical, Bevel, Worm and Worm Wheel

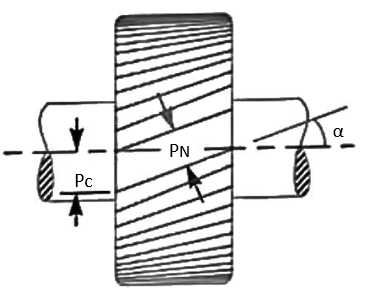
Q1) Define helix angle, axial pitch & normal pitch.

Ans.

Helix angle:- It is a constant angle made by the helices with the axis of rotation.

Axial pitch:- It is the distance, parallel to the axis, between similar faces of adjacent teeth. It is the same as circular pitch and is therefore denoted by

The actual pitch may also be defined as the circular pitch in the plane of rotation or the diametral plane.

Normal pitch:- it is the distance between similar faces of adjacent teeth along a helix on the pitch cylinders normal to the teeth. It is denoted by

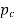
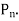
The normal pitch may also be defined as the circular pitch in the normal plane which is a plane perpendicular to the teeth. Mathematically, normal pitch,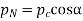

Q2) Write down geometrical relationships for helical gears.

Ans.

Though the proportions for helical gears are not standardized, yet the following are recommended by American gear manufacturers association.

Pressure angle in the plane of rotation, ϕ =15° to 25°

Helix angle α = 20° to 45°

Addendum=0.8m

Dedendum= 1m

Minimum total depth= 1.8m

Minimum clearance=0.2m

Thickness of tooth=1.5708m

Q3) Explain tooth forces in helical gears.

Ans.

The force exerted by a helical gear on its matting gear acts normal to the contacting surfaces if friction is neglected.

However, a normal force in the case of helical gears has three components.

Apart from tangential and radial components that are present in spur gears, a third component parallel to the axis of the shaft of the gear also exist.

This is known as the actual is the thrust force component.

The figure shows the normal force and its component acting on a helical gear.

The gear shown is the driving gear and the forces are exerted on it by the driving gear.

Let 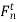=total normal force

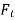=tangential force

=axial force

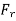=radial force

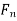=normal force in the plane of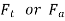

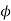=Pressure angle

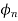=Normal pressure angle

=Helix angle

Then

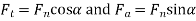
Q4) Derive an expression for the efficiency of the spiral gear.

Ans.

A pair of spiral gears 1 and 2 in the mesh is shown in the figure.

Let the gear 1 be the driver and the gear 2 the driven.

The forces acting on each of a pair of teeth in contact are shown in the figure.

The forces are assumed to act at the center of the width of each teeth and in-plane tangential to the pitch cylinders.

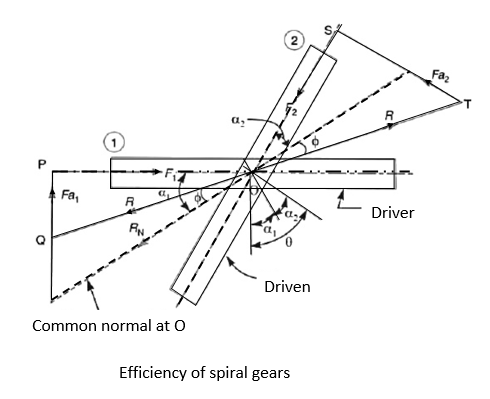
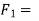force applied tangentially on the driver,

=resisting force acting tangentially on the driven.

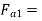axial or end thrust on the driver

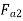=axial or end thrust on the driven

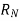= normal reaction at the point of contact,

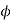= Angle of friction

R= resultant reaction at the point of contact

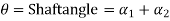
From triangle OPQ,

Work input to the driver

From triangle OST,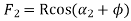

The work output of the driven

The efficiency of spiral gears,

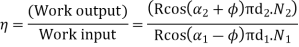
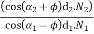………… 1

t pitch circle diameter of gear 1,

And pitch circle diameter of Gear 2

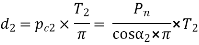
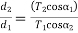……………. 2

We know that ……………. 3

Multiplying equation 2 and 3 we get

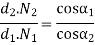
Substituting this value in equation 1 we get

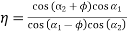…….. 4

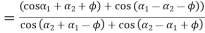
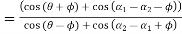………… 5

Since the angles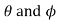 are constants, therefore the efficiency will be maximum, when.
) Is maximum.

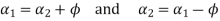
Since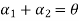
, therefore

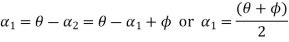
Similarly,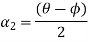

Similarly, 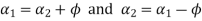in the equation we get

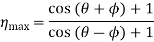
Q5) Derive an expression for virtual teeth for helical gears.

Ans.

The virtual or equivalent number of teeth for helical gear may be defined as the number of teeth that can be generated on the surface of a cylinder having a radius equal to the radius of curvature at a point at the tip of the minor axis of an ellipse obtained by taking a section of the gear in the normal plane.

The pitch cylinder of the helical gear is cut by plane A-A which is normal to the tooth elements as shown in the figure.

When a cylinder is cut by a plane, which is inclined to its base, the cut section is an ellipse.

We will apply this rule of engineering drawing to the pitch cylinder.

The intersection of the plane A-A, which is inclined to the base of the cylinder and the pitch cylinder produces an ellipse.

This ellipse is shown by the dotted line.

The semi-major and semi-minor axis of the ellipse is

respectively.

It can be proved from analytical geometry that the radius of curvature r' at point B is given by,

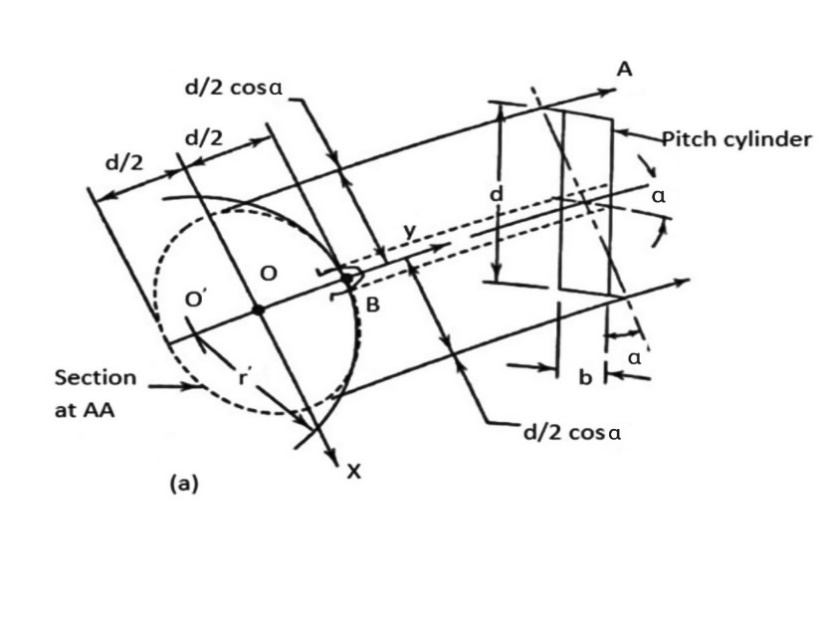
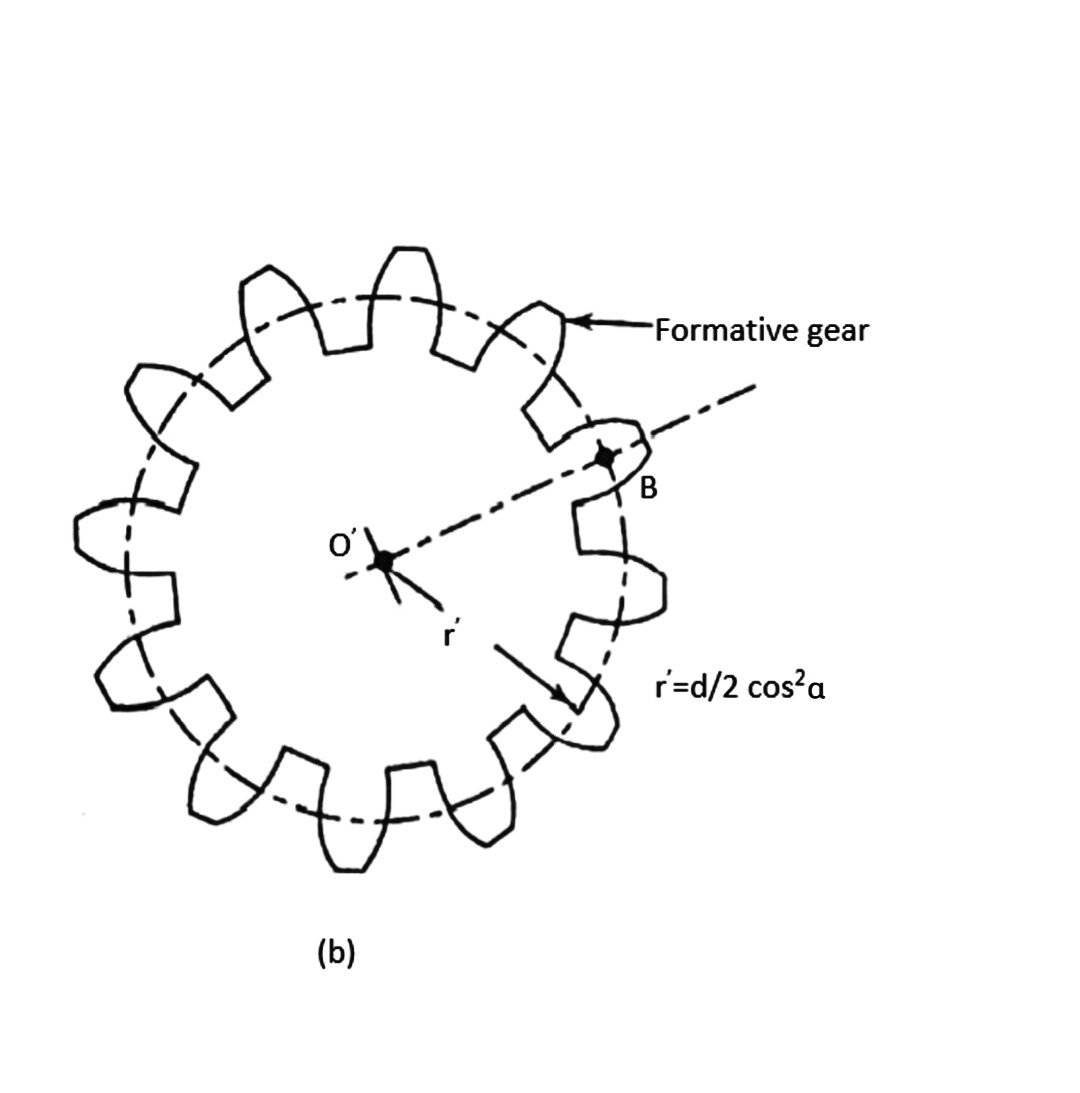
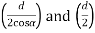
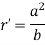
Where a and b are semi-major and semi-minor axis respectively.

Substituting the values of a and b in the expression for r',

In the design of helical gears, an imaginary spur gear is considered in-plane A-A with the center at O' having a pitch Circle radius of r' and module m.

It is called a formative or virtual spur gear. This formative gear is shown in the figure.

The pitch circle diameter d' of the virtual gear is given by

The number of teeth z' on this imaginary spur gear is called the virtual number of teeth. It is given by

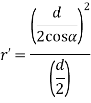
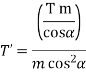
Where, T= actual number of teeth on a helical gear, and

=Helix angle

Q6) Define pitch cone, addendum angle, dedendum angle, face angle, root angle, back cone & backing.

Ans.

Pitch cone:- It is a cone containing the pitch elements of the teeth.

Addendum angle:- It is the angle subtended by the addendum of the tooth at the cone center. It is denoted by

Mathematically, addendum angle,

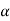
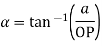
a= Addendum and OP=Cone distance

3. Dedendum angle:- It is the angle subtended by the dedendum of the tooth at the cone center. It is denoted by 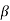mathematically, dedendum angle,

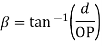
d= Dedendum and OP=Cone distance

4. Face angle:- It is the angle subtended by the face of the tooth at the cone center. It is denoted by 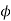. The face angle is equal to the pitch angle plus addendum angle.

5. Root angle:- It is the angle subtended by the root of the tooth at the cone center. It is denoted by . It is equal to the pitch angle minus the dedendum angle.

6. Back cone:- It is an imaginary cone, perpendicular to the pitch cone at the end of the tooth.

7. Backing:- It is the distance of the pitch. From the back of the boss, parallel to the pitch point of the gear. It is denoted by B.

Q7) Write down geometrical relationships for bevel gears.

Ans.

The proportions for the bevel gears may be taken as follows:-

Addendum a=1m

Dedendum d =1.2m

Clearance = 0.2m

Working depth =2m

The thickness of tooth= 1.5708m

Where m is the module.

Q8) Explain tooth forces in bevel gears.

Ans.

Consider a bevel gear and pinion in the mesh as shown in the figure.

The normal force on the tooth is perpendicular to the tooth profile and thus makes an angle equal to the pressure angle to the Pitch Circle.

Thus, the normal force can be resolved into two components, one is the tangential component and the other is the radial component.

The tangential component produces the bearing reactions while the radial component produces end thrust in the shafts.

The magnitude of the tangential and radial components is as follows:

These forces are considered to act at the mean radius.

From the geometry of the figure, we find that

Now the radial force acting at the mean radius may be further resolved into 2 components

in the axial and radial directions as shown in the figure.

Therefore, the axial force acting on the pinion shaft,

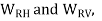
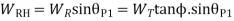
And the radial force acting on the pinion shaft,

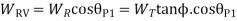
A little consideration will show that the axial force on the pinion shaft is equal to the radial force on the gear shaft, but their directions are opposite.

Similarly, the radial force on the pinion shaft is equal to the axial force on the gear shaft but act in opposite directions.

Q9) Define axial pitch, lead, lead angle, normal pitch & helix angle.

Ans.

Axial pitch:- It is also known as linear pitch of a worm. It is the distance measured actually from a point on one thread to the corresponding point on the adjacent thread on the worm, as shown in the figure. It may be noted that the axial pitch of a worm is equal to the circular pitch of the mating worm gear when the shafts are at right angles.

2. Lead:- It is the linear distance through which a point on a thread moves ahead in one revolution of the worm. For single start thread lead is equal to the axial pitch, but for multiple start threads, lead is equal to the product of pitch and number of stars. Mathematically,

= axial pitch; n=number of starts.

3. Lead angle:- It is the angle between the tangent to the thread helix on the pitch cylinder and the plane normal to the axis of the worm. It is denoted by .

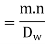
m =module, and

=pitch circle diameter of the worm.

4. Normal pitch:- It is the distance measured along the normal to the threads between two corresponding points on two adjacent threads of the worm. Mathematically,

Normal pitch,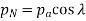

5. Helix angle:- It is the angle between the tangent to the thread helix on the pitch cylinder and the axis of the worm. It is denoted by.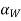

Q10) Write down geometrical relationships for worm & worm wheel.

Ans.

Proportions for the worm

SR.No.	Particulars	Single and double threaded worms	Triple and quadruple threaded worms
1	Normal-pressure angle	14.5°	20°
2	Pitch circle diameter for worms integral with the shaft
3	Pitch circle diameter for worms’ board to fit over the shaft	2.4
4	Maximum bore for shaft
5	Hub diameter
6	Face length
7	Depth of tooth
8	Addendum

Proportions for worm gear

Sr No.	Particulars	Single and double threads	Triple and quadruple threads
1	Normal-pressure angle		20
2	Outside diameter
3	Throat diameter
4	Face width
5	The radius of gear face
6	The radius of gear rim

Q11) Explain tooth forces in worm & worm wheel.

A11)

When the worm gearing is transmitting power, the forces acting on the worm are similar to those on a power screw.

Forces on a worm gear are equal in magnitude to that of the worm, but opposite in direction to those shown in fig

The various forces acting on the form may be determined as follows:

Tangential force on the worm

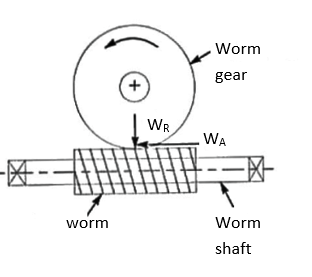
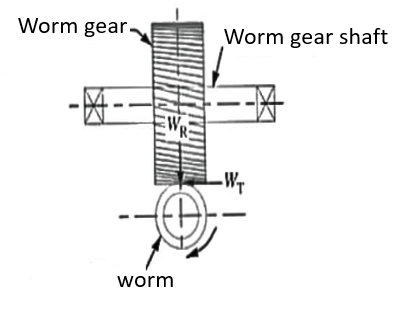
= Axial force or thrust on the worm gear.

The tangential force on the worm produces a twisting moment of magnitude 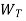x 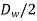and bands the worm in the horizontal plane.

2. The axial force of thrust on the worm

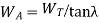=tangential force on the worm gear.

The axial force on the worm tends to move the worm axially, includes an axial load on the bearings and bends the worm in a vertical plane with a bending moment of magnitude x .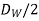

3. Radial or separating force on the worm

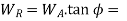Radial or separating force on the worm gear.

The radial or separating force tends to force the worm and worm gear out of the match. This force also bends the worm in the vertical plane.

Sign Up