UNIT 4
Statistical Tools and Interpretation
Q1) The following data represent the income distribution of 100 families. Calculate mean income of 100 families?
Income | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 | 80-90 | 90-100 |
No. Of families | 8 | 12 | 25 | 22 | 16 | 11 | 6 |
A1)
Income | No. Of families | Xm (Mid point) | FXm |
30-40 | 8 | 35 | 280 |
40-50 | 12 | 34 | 408 |
50-60 | 25 | 55 | 1375 |
60-70 | 22 | 65 | 1430 |
70-80 | 16 | 75 | 1200 |
80-90 | 11 | 85 | 935 |
90-100 | 6 | 95 | 570 |
| n = 100 |
| ∑f Xm = 6198 |
X = ∑f Xm/n = 6330/100 = 63.30
Mean = 63.30
Q2) calculate the mean number of hours per week spent by each student in texting message.
Time per week | 0 - 5 | 5 - 10 | 10 - 15 | 15 - 20 | 20 - 25 | 25 – 30 |
No. Of students | 8 | 11 | 15 | 12 | 9 | 5 |
A2)
Time per week (X) | No. Of students (F) | Mid point X | XF |
0 - 5 | 8 | 2.5 | 20 |
5 – 10 | 11 | 7.5 | 82.5 |
10 - 15 | 15 | 12.5 | 187.5 |
15 - 20 | 12 | 17.5 | 210 |
20 - 25 | 9 | 22.5 | 202.5 |
25 – 30 | 5 | 27.5 | 137.5 |
| 60 |
| 840 |
Mean = 840/60 = 14
Q3) The following table of grouped data represents the weights (in pounds) of all 100 babies born at a local hospital last year.
Weight (pounds) | Number of Babies |
[3−5) | 8 |
[5−7) | 25 |
[7−9) | 45 |
[9−11) | 18 |
[11−13) | 4 |
A3)
Weight (pounds) | Number of Babies | Mid point X | XF |
[3−5) | 8 | 4 | 32 |
[5−7) | 25 | 6 | 150 |
[7−9) | 45 | 8 | 360 |
[9−11) | 18 | 10 | 180 |
[11−13) | 4 | 12 | 48 |
| 100 |
| 770 |
Mean = 770/100 = 7.7
Q4) find the median of the table given below
Marks obtained | No. Of students |
20 | 6 |
25 | 20 |
28 | 24 |
29 | 28 |
33 | 15 |
38 | 4 |
42 | 2 |
43 | 1 |
A4)
Marks obtained | No. Of students | Cf |
20 | 6 | 6 |
25 | 20 | 26 (20+6) |
28 | 24 | 50 (26+24) |
29 | 28 | 78 |
33 | 15 | 93 |
38 | 4 | 97 |
42 | 2 | 99 |
43 | 1 | 100 |
Median = (n+1)/2 = 100+1/2 = 50.5
Median = (28+29)/2 = 28.5
Q5) Calculate the median
Marks | No. Of students |
0-4 | 2 |
5-9 | 8 |
10-14 | 14 |
15-19 | 17 |
20-24 | 9 |
A5)
Marks | No. Of students | CF |
0-4 | 2 | 2 |
5-9 | 8 | 10 |
10-14 | 14 | 24 |
15-19 | 17 | 41 |
20-24 | 9 | 50 |
| 50 |
|
n = 50
n = 50/2= 25
2
The category containing n/2 is 15 -19
Lb = 15
Cfp = 24
f = 17
Ci = 4
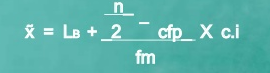
Median = 15 + 25-24 *4 = 15.23
17
Q6) In a class of 30 students marks obtained by students in science out of 50 is tabulated below. Calculate the mode of the given data.
Marks obtained | No. Of students |
10 -20 | 5 |
20 – 30 | 12 |
30 – 40 | 8 |
40 – 50 | 5 |
A6)
The group with the highest frequency is the modal group: - 20 -30
D1 = 12 - 5 = 7
D2 = 12 - 8 = 4
Mode = L1 + (L2 – L1) d1
d1 +d2
mode = 20 + (30-20) 7 = 20+10 (7/11) = 26.36
7+4
Mode = 61.8
Q7) Calculate D7 from the following data:
Class | 2 - 4 | 4 - 6 | 6 - 8 | 8 - 10 |
Frequency | 3 | 4 | 2 | 1 |
A7)
In the case of Frequency Distribution, Deciles can be calculated by using the formula:
Di = l1 +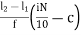 
Class interval | F | CF |
2 – 4 | 3 | 3 |
4 – 6 | 4 | 7 |
6 – 8 | 2 | 9 |
8 – 10 | 1 | 10 |
Total | n = 10 |
|
Here n = 10
Class with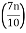 
th value of the observation in CF column
= 
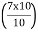th value of the observation in CF column
= 7th value of the observation in CF column and it lies in the class 6 – 8
Therefore, D7 class is 6 – 8
The lower boundary point of 6 – 8 is 6.
Therefore, L = 6
D7 = L +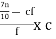 
= 6 + 
x 2
= 6 + 0
= 6
Q8) calculate quartile deviation from the following test scores
Sl. N o | Test scores |
1 | 17 |
2 | 17 |
3 | 26 |
4 | 27 |
5 | 30 |
6 | 30 |
7 | 31 |
8 | 37 |
A8)
First quartile (Q1)
Qi= [i * (n + 1) /4] th observation
Q1= [1 * (8 + 1) /4] th observation
Q1 = 2.25 th observation
Thus, 2.25 th observation lies between the 2nd and 3rd value in the ordered group, between frequency 17 and 26
First quartile (Q1) is calculated as
Q1 = 2nd observation +0.75 * (3rd observation - 2nd observation)
Q1 = 17 + 0.75 * (26 – 17) = 23.75
Third quartile (Q3)
Qi= [i * (n + 1) /4] th observation
Q3= [3 * (8 + 1) /4] th observation
Q3 = 6.75 th observation
So, 6.75 th observation lies between the 6th and 7th value in the ordered group, between frequency 30 and 31
Third quartile (Q3) is calculated as
Q3 = 6th observation +0.25 * (7th observation – 6th observation)
Q3 = 30 + 0.25 * (31 – 30) = 30.25
Now using the quartiles values Q1 and Q3, we will calculate the quartile deviation.
QD = (Q3 - Q1) / 2
QD = (30.25 – 23.75) / 2 = 3.25
Q9)Calculate mean deviation from the median
Class | 5 -15 | 15 – 25 | 25 - 35 | 35 - 45 | 45 – 55 |
Frequency | 5 | 9 | 7 | 3 | 8 |
A9)
x | f | Cf | Mid point x | x –median | F(x-m) |
5 -15 | 5 | 5 | 10 | 17.42 | 87.1 |
15 -25 | 9 | 14 | 20 | 7.42 | 66.78 |
25 -35 | 7 | 21 | 30 | 2.58 | 18.06 |
35 -45 | 3 | 24 | 40 | 12.58 | 37.74 |
45- 55 | 8 | 32 | 50 | 22.58 | 180.64 |
| 32 |
|
|
| 390.32 |
Since n/2 = 32/2 = 16, therefore the class is 25 – 35 is the median.
Median = 
Median = 25+16-14 *10 = 27.42
7
MD from median is 390.32/32 = 12.91
Q10)Calculate the standard deviation using the direct method
Class interval | Frequency |
30 – 39 | 3 |
40 – 49 | 1 |
50 – 59 | 8 |
60 – 69 | 10 |
70 – 79 | 7 |
80 – 89 | 7 |
90 – 99 | 4 |
A10)
Class interval | Frequency | Mid point x | Fx |  |  |  |
30 – 39 | 3 | 34.5 | 103.5 | -33.5 | 1122.25 | 3366.75 |
40 – 49 | 1 | 44.5 | 44.5 | -23.5 | 552.25 | 552.25 |
50 – 59 | 8 | 54.5 | 436.0 | -13.5 | 182.25 | 1458 |
60 – 69 | 10 | 64.5 | 645.0 | -3.5 | 12.25 | 122.5 |
70 – 79 | 7 | 74.5 | 521.5 | 6.5 | 42.25 | 295.75 |
80 – 89 | 7 | 84.5 | 591.5 | 16.5 | 272.25 | 1905.75 |
90 – 99 | 4 | 94.5 | 378.0 | 26.5 | 702.25 | 2809 |
| 40 |
| 2720 |
|
| 10510 |
Mean = 2720/40 = 68
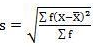
SD = √10510/40 = 16.20
