UNIT 1
Elementary Ideas of Arithmetic Progression
Q1) Find the value of n. If a = 10, d = 5, an = 95.
A1)
Given, a = 10, d = 5, an = 95
From the formula of general term, we have:
an = a + (n − 1) × d
95 = 10 + (n − 1) × 5
(n − 1) × 5 = 95 – 10 = 85
(n − 1) = 85/ 5
(n − 1) = 17
n = 17 + 1
n = 18
Q2) Find the 20th term for the given AP:3, 5, 7, 9, ……
A2) Given,
3, 5, 7, 9, ……
a = 3, d = 5 – 3 = 2, n = 20
an = a + (n − 1) × d
a20 = 3 + (20 − 1) × 2
a20 = 3 + 38
⇒a20 = 41
Q3) How many terms are added in 24+20+16+ ....... 10 make the sum 72.
A3)
We know that sum to first n terms of an A.P. = Sn = n/2 [2a + (n – l) d]
Let the sum of n terms be 72, a = 24, d = -4

Q4) The sum of three numbers in a GP is 26 and their product is 216. Ind the numbers.
A4) Let the numbers be a/r, a, ar.
=> (a / r) + a + a r = 26
=> a (1 + r + r2) / r = 26
Also, it is given that product = 216
=> (a / r) x (a) x (a r) = 216
=> a3 = 216
=> a = 6
=> 6 (1 + r + r2) / r = 26
=> (1 + r + r2) / r = 26 / 6 = 13 / 3
=> 3 + 3 r + 3 r2 = 13 r
=> 3 r2 – 10 r + 3 = 0
=> (r – 3) (r – (1 / 3) ) = 0
=> r = 3 or r = 1 / 3
Thus, the required numbers are 2, 6 and 18
Q5) Determine the 4th and 8th term of the harmonic progression 6, 4, 3,…
A5)
Given:
H.P = 6, 4, 3
Now, let us take the arithmetic progression from the given H.P
A.P = ⅙, ¼, ⅓, ….
Here, T2 -T1 = T3 -T2 = 1/12 = d
So, in order to find the 4th term of an A. P, use the formula,
The nth term of an A.P = a+(n-1)d
Here, a = ⅙, d= 1/12
Now, we have to find the 4th term.
So, take n=4
Now put the values in the formula.
4th term of an A.P = (⅙) +(4-1)(1/12)
= (⅙)+(3/12)
= (⅙)+ (¼)
= 5/12
Similarly,
8th term of an A.P = (⅙) +(8-1)(1/12)
= (⅙)+(7/12)
= 9/12
Since H.P is the reciprocal of an A.P, we can write the values as:
4th term of an H.P = 1/4th term of an A.P = 12/5
8th term of an H.P = 1/8th term of an A.P = 12/9 = 4/3
Q6) Compute the 16th term of HP if the 6th and 11th term of HP are 10 and 18 respectively.
A6)
The H.P is written in terms of A.P are given below:
6th term of A.P = a+5d = 1/10 —- (1)
11th term of A.P = a+10d = 1/18 ……(2)
By solving these two equations, we get
a =13/90, and d = -2/ 225
To find 16th term, we can write the expression in the form,
a+15d = (13/90) – (2/15) = 1/90
Thus, the 16th term of an H.P = 1/16th term of an A.P = 90
Therefore, the 16th term of the H.P is 90.
Q7) Find the number of permutations and combinations if n = 12 and r = 2.
A7)
Given,
n = 12
r = 2
Using the formula given above:
Permutation:

Combination:
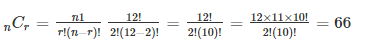
Q8) Expand (x/3 + 2/y)4
A8)

Q9) Using binominal theorem , (√2 + 1)5 + (√2 − 1)5
A9)
We have
(x + y)5 + (x – y)5 = 2[5C0 x5 + 5C2 x3 y2 + 5C4 xy4]
= 2(x5 + 10 x3 y2 + 5xy4)
Now (√2 + 1)5 + (√2 − 1)5 = 2[(√2)5 + 10(√2)3(1)2 + 5(√2)(1)4]
=58√2
Q10) Find the number of terms in (1 + 2x +x2)50
A10)
(1 + 2x + x2)50 = [(1 + x)2]50 = (1 + x)100
The number of terms = (100 + 1) = 101