UNIT 2
Set Theory
Q1) Explain set theory
A1) Set Theory is a branch of mathematics in which we study about sets and their properties. Georg Cantor (1845-1918), a German mathematician, initiated the concept ‘Theory of sets’ or ‘Set Theory’.
Definition
A set is any collection of objects specified in such a way that we can determine whether a given object is or is not in the collection. In other words a set is the collection of objects. These objects are called elements or members of the set.
The following points are noted while writing a set
- Set are usually denoted by capital letters A, B, S, etc.
- The elements of the set are usually denoted by small letters a, b, t, etc
Examples –
A = {a, b,c, d}
C = {maths, science, history, English}
The symbol  is used to denote belongs to or is an element of or is a member of a set.
is used to denote belongs to or is an element of or is a member of a set.
 a is an element of set A
a is an element of set A
 a is not an element of set A
a is not an element of set A
Representation of set
- Statement form - In this form, the well-defined description of the elements of the set is given.
Ex - The set of all even number less than 10.
2. Roaster form - In this form, elements are listed within the pair of brackets {} and are separated by commas
Ex - Let N is the set of natural numbers less than 5.
N = { 1 , 2 , 3, 4 }.
3. Set builder form - In Set-builder set is described by a property that its member must satisfy.
- {x : x is even number divisible by 6 and less than 100}
Types of sets
- Empty sets – the sets that contains no members is called empty sets or null sets. The empty set is written as { }
- Equal sets - Two sets are said to be equal if both have same elements. For example A = {1, 3, 9, 7} and B = {3, 1, 7, 9} are equal sets.
- Subsets – sets which are the part of another set is called subsets of the original sets. Ex – if A = {1,2,3,4} and B = {1,2}. Then B is the subset of A
- Power set – if ‘A’ is any set then one set of all are subset of A that it is called a power set. Ex - What is the power set of {0,1,2}?
Solution: All possible subsets
{∅}, {0}, {1}, {2}, {0,1}, {0,2}, {1,2}, {0,1,2}.
Q2) Explain Union Intersection and Difference of Sets
A2)
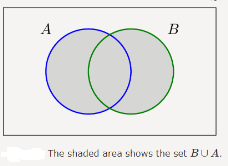
The union of two sets contains all the elements contained in either set (or both sets).
The union is notated A ⋃ B. A∪B={x:x∈A or x∈B}

The intersection of two sets contains only the elements that are in both sets.
The intersection is notated A ⋂ B.A∩B={x:x∈A and x∈B}
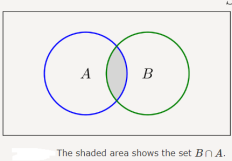
The difference is the set of all thongs that are in A but not in B.
A−B={x:x∈A and x∉B}

Q3) Consider the sets: A = {red, green, blue} B = {red, yellow, orange}
Find A ⋃ B, A ⋂ B, A-B
A3)
Find A ⋃ B
The union contains all the elements in either set: A ⋃ B = {red, green, blue, yellow, orange}
Note we only list red once
Find A ⋂ B
The intersection contains all the elements in both sets: A ⋂ B = {red}
Find A-B
The difference contains A-B = {green, blue}
Q4) A={a,b,c,d,e} , B={d,e,f} and C={1,2,3} .
Find A∪B, A∩B, A−B, B−A, (A−B)∪(B−A ), A∪C , A∩C , A−C, (A∩C)∪(A−C), (A∩B)×B , (A×C)∪(B×C)
A4)
A∪B={a,b,c,d,e,f}
A∩B={d,e}
A−B={a,b,c}
B−A={f}
(A−B)∪(B−A)={a,b,c,f}
A∪C={a,b,c,d,e,1,2,3}
A∩C={∅}
A−C={a,b,c,d,e}
(A∩C)∪(A−C)={a,b,c,d,e}
(A∩B)×B={(d,d),(d,e),(d,f),(e,d),(e,e),(e,f)}
(A×C)∪(B×C)={(d,1),(d,2),(d,3),(e,1),(e,2),(e,3)}
Q5) If the universal set is given by S={1,2,3,4,5,6}, and A={1,2}, B={2,4,5},C={1,5,6} are three sets, find the following sets:
A∪B
 A∩B
A∩B
A
 B
B
A5)
A∪B={1,2,4,5}.
A∩B={2}.


 A ={3,4,5,6} (A consists of elements that are in S but not in A).
A ={3,4,5,6} (A consists of elements that are in S but not in A).
B ={1,3,6}.
Q6) Multiply matrix
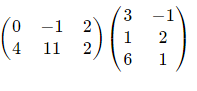
A6)
This is 2×3 times 3×2, which will give us a 2×2 answer

Our answer is a 2×2 matrix.
Q7) Multiply matrix
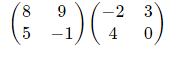
A7)

Q8) If possible, find BA and AB
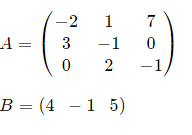
A8)
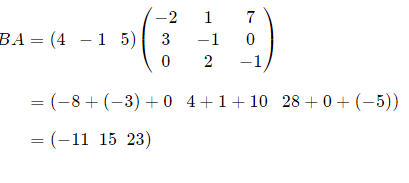
AB is not possible. (3 × 3) × (1 × 3)
Q9) Find the value of the variable y for the equation y = 2x2 when x = 5
A9)
Given equation: y = 2x2
Here x is called independent variable
Y is called dependent variable
When x = 5, the value of y becomes:
y = 2x2
Now, substituting x = 5 in the given equation, we get
y = 2(5)2
y = 2(25)
y = 50
Therefore, the value of y is 50, when x = 5
Q10) y = f(x) = 3x + 4
Find f(0), Find f(1), Find f(-1)
A10)
Find f(0). This means find the value of y when x equals 0.
f(0) = 3 times 0 plus 4
f(0) = 3(0) + 4 = 4
Find f(1). This means find the value of y when x equals 1.
f(1) = 3 times 1 plus 4
f(1) = 3(1) + 4 = 7
Find f(-1). This means find the value of y when x equals -1.
f(-1) = 3 times (-1) plus 4
f(1) = 3(-1) + 4 = 1