Unit – 2

Equilibrium

Q1) Explain the Reversible and Irreversible reaction?

A1) Reversible reaction

Any changes which can be reversed or are a temporary conversion are known as reversible changes. The reactions which are reversible are called reversible reactions. In this reaction, one substance is modified into another form but a new compound is not formed. Processes such as melting, boiling, evaporation, freezing, condensation, dissolution are reversible changes. Few examples are melting of wax, freezing of ice, boiling water which evaporates as steam and condenses back to water.

Reactions are an interaction of two or more compounds called reactants to produce a product(s). In a reversible reaction, reactants and products formed are connected by a two-way arrow (⇌). This means reactants can be obtained back from the products.

Consider the reaction below,

A +B ⇌ C + D

Here, A and B are two reactants which react to give C and D. The two-headed arrow indicates that reaction is reversible and the reactants, A and B can be obtained from C and D.

Irreversible reaction

In contrast to reversible reaction, irreversible changes are permanent changes. Reactants react to form an entirely new compound and cannot be reversed. Heating, burning, mixing, powdering are few processes which cause irreversible changes. A common observable example is the cooking of raw egg which can’t be converted back to its original form. Ash obtained by the combustion of paper or any other substances is another example.

When a reaction is taking place in a unidirectional way such reactions are called irreversible reactions. In such reactions in a period of time reactants react completely to form a product. Here reaction is denoted by a one-way arrow (→).

For example,

A → B +C

Here, A is the reactant which is completely converted into products B and C which do not react to form A.

DEFINITION OF CHEMICAL CHANGE - DEFINITION

A change in which one or more new substances are formed is called a chemical change. A chemical change is also called a chemical reaction. 
Examples are burning of any substance, rusting of iron.

REVERSIBLE REACTION - DEFINITION

A reversible reaction is a chemical reaction that can proceed in both forward and backward direction.

aA+bB⇋cC+dD

A and B can react to form C and D or, in the reverse reaction, C and D can react to form A and B.

IRREVERSIBLE REACTIONS - DEFINITION

If a reaction cannot take place in the reverse direction, i.e., the products formed do not react to give back the reactants under the same condition is called an irreversible reaction.

BaCl2​(aq)+Na2​SO4​(aq)→BaSO4​(s)+NaCl(aq)

Q2) What is the Equilibrium Constant for Homogeneous and Heterogeneous Reaction?

A2) In order to simplify the problems and understand the concept, we divide such reactions into different categories, namely, the homogeneous reactions, where the components involved in the reaction are present in the same phase and the heterogeneous reactions, where the components involved are present in different phases. The methods of dealing with both the reactions are different and so is the determination of the equilibrium state. In this section, we will learn about a homogeneous equilibrium and the calculation of equilibrium constant for a homogeneous reaction.

Equilibrium Constant for Homogeneous Reaction

Let us consider a homogeneous system, given by the following reaction

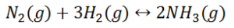
Here, we see that gaseous nitrogen reacts with gaseous hydrogen to form gaseous ammonia. Let us now calculate the equilibrium constant for the above reaction.

In terms of the molar concentration of the components in the reaction, we can write

As we know, for reactions involving gases, we express the equilibrium concentration in terms of the partial pressure.

Using the ideal gas equation,

Where P is the pressure of the system, V is the volume of the system, n is the number of moles of components present in the system, R is the universal gas constant and T is the temperature of the system.

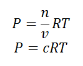
Here, c is the concentration of the system. We can also write it as,

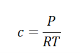
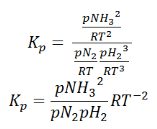
So, equilibrium constant can also be written as,

Here, we note that the general expression for Kc and Kp can be written as,

Where Δn is defined as the number of moles of gaseous products – the number of moles of gaseous reactants.

Equilibrium Constant for Heterogeneous Reaction

When the state of equilibrium in a system has components in more than one phase it is termed as a heterogeneous equilibrium. For example, if we take a container with ice and water at a temperature that is allowing the existence of both the phases simultaneously, such that, both ice and water are present in a state of equilibrium. This state is termed as heterogeneous equilibrium.

In terms of its equation, this can be written as:

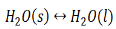
In another example, we can consider an aqueous solution of a solid such as calcium hydroxide. We notice that the solid calcium hydroxide is in equilibrium with its saturated solution.

Writing the equilibrium constant for heterogeneous reactions is different from that of the homogeneous reactions. For example, consider the thermal dissociation of calcium carbonate into calcium oxide and carbon dioxide. Here, we can see that the equilibrium constant for the dissociation of the reactant into its products is only dependent on the gaseous component, as the solid and the liquid reactants are considered to be constant.

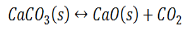
Here, the components CaCO3 and CaO are solids, so their molar concentration remains constant throughout the reaction. Therefore, the equilibrium constant can be written as,

Also, in terms of Kp, we can write

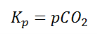
Where p denotes the partial pressure. In other words, we can state that, at a given temperature, there is a constant concentration or partial pressure of CO2 in the equilibrium reaction with CaO and CaCO3. 

Representation of the Equilibrium Constant

For a balanced reaction of the type,

aA + bB ⇌ cC + dD

According to the law of mass action, the constant value obtained by relating equilibrium concentrations of reactants and products is called the equilibrium constant. For the forward reaction, this is given by

Kc = [C]c[D]d

          [A]a[B]b

The equilibrium constant for the reverse reaction is the inverse of the forward reaction and is given by:

K′c = 1       = [A]a[B]b

           Kc      [C]c[D]d

If the coefficients of the chemical equation are multiplied by a factor ‘n’ then the equilibrium constant is raised by the power ‘n’ i.e., the constant becomes Knc.

Q3) Define the Le Chatelier’s Principle?

A3) Le Chatelier’s principles, also known as the equilibrium law, are used to predict the effect of some changes on a system in chemical equilibrium (such as the change in temperature or pressure). The principle is named after the French chemist Henry Louis Le Chatelier.

Le Chatelier said that equilibrium adjusts the forward and backward reactions in such a way to accept the changes affecting the equilibrium conditions.

Le Chatelier's principle can be used to predict the behaviour of a system due to changes in pressure, temperature, or concentration. Le Chatelier's principle implies that the addition of heat to a reaction will favour the endothermic direction of a reaction as this reduces the amount of heat produced in the system.

According to Le Chatelier’s Principles,

Application of Le Chatelier’s

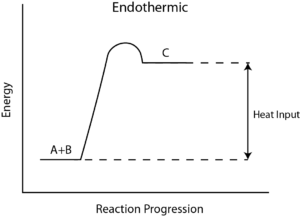
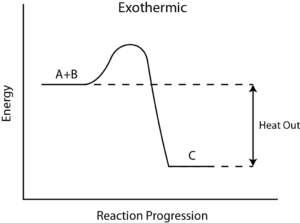
Q4) What is Reaction Enthalpy?

A4) Reaction enthalpy

During any chemical reaction, heat is either absorbed or given out. The heat exchange between the chemical reaction and its environment is reaction enthalpy (H). This cannot be measured directly. For this, there is a measurement of change in the temperature of a reaction over time to the final change in enthalpy denoted by ΔH.

From the value of ΔH, whether in a reaction heat is absorbed from the environment [endothermic] or is given off to the environment [exothermic] is determined. In general, ΔH is given as, ΔH = m×s×ΔT, where m is the mass of reactants, s is the specific heat of products, and ΔT is a change in temperature during the completion of the reaction.

How to Calculate the Reaction Enthalpy?

To find enthalpy of a chemical reaction we need to follow the below mentioned steps.

Finally, we will get the enthalpy of the chemical reaction.

Example of Enthalpy Calculation

Hydrogen reacts with oxygen to give water. The chemical reaction is,

2H2 + O2   →   2H2O

Reactants       Products

2H2 + O2 = 2H2O

2×[2g] 1×[32g] = 4g + 32g =36g

2H2 + O2 = H2O

The specific heat of water is 4.2 joule/gram°C

ΔT = T1 – T2 (T1 = 185K and T2 = 95 K) = 185K – 95K

ΔT = -90K

In the above reaction, the reactants had more temperature, and after the completion of the reaction, the product got cooled off.

ΔH = 36g×42 jg-1k-1 × (-90) K = -13608 joule

ΔH < 0

This makes logical sense since hot gases hydrogen (H2) and oxygen(O2) react together and let off heat to the environment. Then water [H2O] forms, indicating that it is an exothermic reaction.

Q5) Write a note on Hess law?

A5) Hess's Law of Constant Heat Summation (or just Hess's Law) states that irrespective of the numerous stages or steps involved in a reaction. The total enthalpy change is the sum of all changes. This law is therefore an expression of enthalpy that enthalpy is a state function.

Introduction

Hess's Law is named after Russian Chemist and Doctor Germain Hess. He was successful in formulating the early principles of thermochemistry. His law on chemistry was published in 1840 in one of his famous papers. Hess’s law was introduced due to enthalpy being a state function, that helps us to calculate the overall change in enthalpy by simple addition of the changes that take place in each step of the reaction till the products are formed. All the individual equations must be balanced and all steps need to proceed at the same temperature. The principle underlying Hess's law does not just apply to Enthalpy and can be used to calculate other state functions like changes in Gibb’s Energy and Entropy.

Definition: Hess's Law

The heat of any reaction ΔH∘fΔHf° for a specific reaction is equal to the sum of the heats of reaction for any set of reactions which in sum are equivalent to the overall reaction:

(Although we have not considered the restriction, applicability of this law requires that all reactions considered proceed under similar conditions: we will consider all reactions to occur at constant pressure.)

Why it works

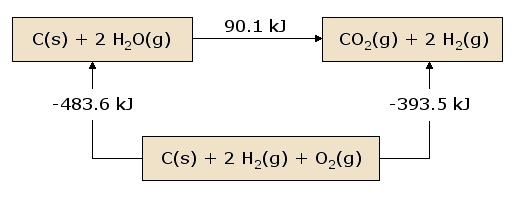
A pictorial view of Hess's Law as applied to the heat of equation. In figure 1, the reactants C(s) + 2 H2O(g) are located in a box that represent the materials that are involved in the reaction prior to the reaction.

 The products CO2(g) + 2 H2(g) are located together in the second box that represent the state the materials that are involved in a reaction., the arrows that connect these two boxes represent the heat of the reaction.

 Now the same materials are placed in the third box, that contains C(s), O2(g), and 2 H2(g).  the box is connected to the other boxes with reaction arrows labelled by heat of reactions.

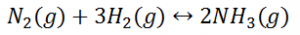
Pictorial View of Hess's Law.

This picture of Hess's Law reveals that the heat of reaction along the "path" directly connecting the reactant state to the product state is exactly equal to the total heat of reaction along the alternative "path" connecting reactants to products via the intermediate state containing C(s)C(s), O2(g)O2(g), and 2 H2(g)H2(g). The net heat that is absorbed or evolved during a reaction, is independent to the path that connects the reactants and products. (This statement is again subject to our restriction that all reactions in the alternative path must occur under constant pressure conditions).

As we begin from the reactant box and go through the complete circuit of other boxes, and leading back to the reactant box, when we consider the net heat of the reaction. We discover that the net heat transferred (again provided that all reactions occur under constant pressure) is exactly zero. This is a state of conservation of energy.: the energy in the reactant state does not depend upon the processes which produced that state.

By perception energy function is the value for the reactants and is independent of how the reactant state is prepared. Similarly, the value of this energy functioning the product state is independent of how the products are prepared. We choose this function, H, so that the change in the function, ΔH = Hproducts - Hreactants, is equal to the heat of reaction q under constant pressure conditions. H, which we call the enthalpy, is a state function, since its value depends only on the state of the materials under consideration, that is, the temperature, pressure and composition of these materials.

For calculating the heats of a reaction, the energy state function H is considered. The figure given below the reactants R being converted to products P. ΔH is a state function that is used to calculate the heat absorbed or released in the reaction. When R and P are used to calculate ΔH along the path, we should consider the two reaction that go through an intermediate state that consists of all the atoms that are involved in a reaction and each in its elemental form. This intermediate stage can be used for all chemical reactions.in the initial figure given above the reaction are C, H, and O, each of which are represented in the intermediate state in elemental form. But in subfigure given below is the ΔH for the overall reaction is now the difference between the ΔH in the formation of the products P from the elements and the ΔH in the formation of the reactants R from the elements.

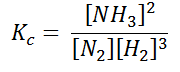
Figure: Calculation of ΔH.

The ΔH values for formation of each material from the elements are thus of general utility in calculating ΔH for any reaction of interest. We therefore define the standard formation reaction for reactant R, as

Elements in standard state  R

and the heat involved in this reaction is the standard enthalpy of formation, designated by ΔHf°. The subscript f, standing for "formation," indicates that the ΔH is for the reaction creating the material from the elements in standard state. The superscript ° indicates that the reactions occur under constant standard pressure conditions of 1 atm. The heat of any reaction can be calculated from

ΔH∘f=ΔH∘f, products−ΔH∘f, reactants

ΔHf°=ΔHf, products°−ΔHf, reactants°

The enthalpy of a reaction is not dependant on the elementary steps, but on the initial state of the reactants and the final state of products. This means that the enthalpy of the reaction scales proportionally to the moles used in the reaction.

Since enthalpy is a state function, it is path independent. Therefore, it does not matter what reactions one uses to obtain the final reaction.

Q6) Define Kirchoff’s law?

A6) A German physicist, Gustav Kirchhoff in 1845, established a set of rules that deal with the conservation of energy and current within electric circuits. These two rules are generally called as: Kirchhoff’s Circuit Laws with one of Kirchhoff’s laws dealing with the current flowing around a closed circuit, Kirchhoff’s Current Law, (KCL) while the other law deals with the voltage sources present in a closed circuit, Kirchhoff’s Voltage Law, (KVL).

Kirchhoff’s First Law – The Current Law, (KCL)

Kirchhoff’s Current Law or KCL, states that the “the total amount of current or charge that enters a junction or a node is exactly equal to the charge that leaves the node, no charge is lost within the node, as the charge has no place to go but to leave the circuit. “. In other words, the algebraic sum of ALL the currents entering and leaving a node must be equal to zero

Kirchhoff’s Second Law – The Voltage Law, (KVL)

Kirchhoff’s Voltage Law or KVL, states that “in any closed loop network, the total voltage around the loop is equal to the sum of all the voltage drops within the same loop” which is also equal to zero. In other words, the algebraic sum of all voltages within the loop must be equal to zero

Components are said to be connected together in Series if the same current value flows through all the components.

Components are said to be connected together in Parallel if they have the same voltage applied across them.

Q7) What do you understand by Bond energy?

A7) It is a measure of a chemical bond strength, which means that it tells the possibility of a pair of atoms to remain bonded in the midst of energy perturbations. Alternatively, it can also be thought as the stability that is obtained when two atoms bond to each other as opposed to their unbounded states.

Bond energy and its determination

The Bond energy is determined by calculating the heat that is required to break one mole of molecules into their individual atoms, it denotes the average energy that is associated with breaking the individual bonds of a molecule. The higher the bond energy, the ‘stronger’ we say the bond is between the two atoms, and the distance between them (bond length) is smaller.

For instance, the HO-H bond in a molecule of water involves 493kJ/mol to break and generate the hydroxide ion (OH–).  Further the breaking of the O-H bond in the hydroxide ion needs an additional of 424 kJ/mol. Therefore, the bond energy of the covalent O-H bonds in water is determined to be the average of the both the values, or 458.9 kJ/mol. These energy values (493 and 424 kJ/mol) are required to break successive O-H bonds in a water molecule and are generally called as ‘bond dissociation energies,’ and they are different from the bond energy. Therefore, the bond energy is the average of the bond dissociation energies in a molecule.

The exact properties of a specific kind of bond are determined in part by the nature of the other bonds in the molecule; for example, the energy and length of the C–H bond will vary depending on what other atoms are bonded to the carbon atom. Similarly, the C-H bond length can vary by as much as 4% between different molecules. For this reason, the values of bond energy and bond length are usually averages taken over a variety of compounds that contain a specific atom pair.

Q8) What is a Thermodynamic System Elaborate?

A8) Thermodynamics is a branch of physics that deals with the relation between other forms of energy and heat, in specific terms, it defines how the thermal energy gets converted to and from other forms of energy and how it affects matter. 

Thermodynamic systems: Thermodynamics in biology is the study of energy transfers that take place in molecules or in a collection of molecules. Generally, when dealing with Thermodynamics, a specific item or a collection of items that we are dealing with is called a system, while everything that's not included in the system, we’ve defined is called the surroundings.

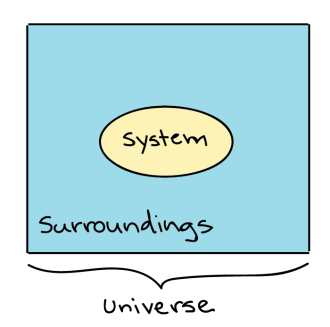
Generalized depiction of the system (a circle), the surroundings (a square surrounding the circle), and the universe (system + surroundings).

For example, if a pot of water is heated on the stove, the system included the stove, pot and water, while the surrounding could be the rest of the items in the kitchen, the decision of what to define as the system is arbitrary (up to the observer), and depending on what you wanted to study, we could equally well make just the water, or the entire house, part of the system. The system and the surroundings together make up the universe.

There are three types of systems in thermodynamics: open, closed, and isolated.

we, like other organisms, are an open system.  We are constantly exchanging matter and energy with our surroundings for e.g.  when we eat a carrot or lift a bag of laundry onto a table, or a simple breathing. In each case, you are exchanging energy and matter with your environment.

Q9) Differentiate between the Intensive and Extensive properties?

A9) Intensive and Extensive properties

Thermodynamic properties can be divided into 2 (two) general classes such as intensive and extensive properties.

An intensive property, is the system’s physical property that does not depend on the size or the amount of material in the system. In contrast the extensive property of a system is not dependent on the system size or the amount of the material. According to the definitions, density, pressure and temperature are intensive properties and volume, internal energy are extensive properties.

Symbols for representing properties: Extensive properties are symbolized by upper case (capital) letter such as V (volume), KE (kinetic energy), PE (potential energy), etc. Intensive properties are symbolized by lower case letters such as v (specific volume), ke (specific kinetic energy), e, u (specific internal energy), h (specific enthalpy), etc. Mole based properties are symbolized by lower case letters with overbars. For example, kinetic energy and molar specific potential energy respectively.

Exceptions: Temperature (intensive), mass (extensive), and number of moles (extensive). The use of symbols for temperature, mass and moles are traditional.

Exceptions:

Symbols for Exceptional Properties

Specific extensive properties, i.e., extensive properties per unit mass are intensive properties. For example: specific volume, specific energy, density, etc.

Q10) What are the types of Thermodynamic Processes?

A10) A thermodynamic process is any process that involves heat energy moving within a system or between systems. 

The four types of thermodynamic process are isobaric, isochoric, isothermal and adiabatic.

The Four Types of Thermodynamic Processes

The state of a given thermodynamics system can be expressed by various parameters like Pressure (P), temperature(T), volume(V) and internal energy(U), if ant two parameters are fixed, suppose pressure (P) and volume (V) of a fixed mass of gas, then the temperature (T) of the gas will be automatically fixed according to the equation PV=RT. No change can be made to T without altering P and V.

Work in Thermodynamic Processes

When the volume (V) of a system alters, it is said that pressure-volume work has occurred. A thermodynamic process occurring in a closed system in such a way that the rate of volume change is slow enough for the pressure (P) to remain constant and uniform throughout the system, is a quasi-static process. In this case, work (W) is represented as:

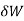= PdV where δW is the infinitesimal work increment by the system ans dV is the infinitesimal volume increment.

Also, W = entire reversible process.

Isobaric Process

An isobaric process is one where the pressure of the system (often a gas) stays constant. 'Iso' means the same, and 'baric' means pressure. Pressure is related to the amount of force that the molecules apply to the walls of the container. Imagine that you have a gas inside a movable piston and you heat that gas up. By heating the gas up, you make the molecules move faster, which would normally increase the pressure. But at the same time the piston expands, increasing the volume and giving the molecules more room to move. Since the walls of the container are now bigger, the pressure can stay the same even though the molecules are moving faster. That makes it an isobaric process.

 Since the pressure (P) is constant in this process, the volume of the system changes. The work (W) done can be calculated as W=P (Vfinal – V initial)

If ΔV is positive (expansion), the work done is positive. For negative ΔV (contraction) the work done is negative.

Isochoric Process

An isochoric process is one where the volume of the system stays constant. Again, 'iso' means the same and 'choric' means volume. Volume is the amount of space the material takes up. So, this would be like heating a gas in a solid, non-expandable container. The molecules would move faster and the pressure would increase, but the size of the container stays the same.

Isochoric Process

The volume remains constant in an isochoric process. Therefore, the system does not do any work (since ΔU=0, PΔV or W is also zero). Such a process in which there is no change in volume can be achieved by placing a thermodynamic system in a closed container which neither contracts nor expands. Thus, from the first law of thermodynamics (Q=ΔU + W), change in internal energy becomes equal to the heat transferred (ΔU = Q) for an isochoric process.

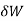= PdV where δW is the infinitesimal work increment by the system ans dV is the infinitesimal volume increment.

Also, W = entire reversible process.

Isothermal Process

An isothermal process is one where the temperature of the system stays constant. Thermal relates to heat, which is in turn related to temperature. Temperature is the average heat (movement) energy of the molecules in a substance.

An example of an isothermal process would be if we took a gas held behind a movable piston and compressed that piston: the volume has decreased, and the pressure behind the piston has increased, since the molecules have less space in which to move. When you compress a piston, you're using energy - you're doing work on the gas - so normally the molecules would gain energy and move faster, and the temperature would increase.  The temperature of the system remains constant in an isothermal process.

W =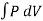

From Gas law

PV = nRT

P = nRT/V . Using the value of P in the work equation

W = nRT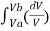

W = nRT ln(VB/VA)

If VB is higher than VA the work done will be positive or else negative

Since internal energy is temperature -dependent, ΔU=0 because the temperature is constant and thus from the first law of thermodynamics (Q= ΔU+W), we will get Q=W

Adiabatic process

The thermodynamic process in which there is no exchange of heat from the system to its surrounding neither during expansion nor during compression.

The adiabatic process can be either reversible or irreversible. Following are the essential conditions for the adiabatic process to take place:

No heat is exchanged with the system in an Adiabatic process (Q=0), its mathematical representation is

PV 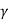= K ( constant)

Also W = 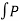dV   substituting the value of P in the work equation

W = K 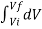/ V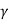

W = K [ (Vf 1-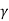 – Vi 1-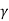) / 1 – ]

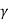 Since Q=0 for an adiabatic process, from the first law of thermodynamics (Q=ΔU+W), we will get ΔU= -W. thus the internal energy will increase if the work done is negative and vice versa.

 Since Q=0 for an adiabatic process, from the first law of thermodynamics (Q=ΔU+W), we will get ΔU= -W. thus the internal energy will increase if the work done is negative and vice versa.

Q11) Define Internal Energy?

A11) The internal energy Eint of a thermodynamic system is, by definition, the sum of the mechanical energies of all the molecules or entities in the system. If the kinetic and potential energies of molecule i are Ki and Ui 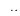 and then the internal energy of the system is the average of the total mechanical energy of all the entities:

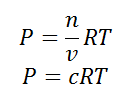
where the summation is over all the molecules of the system, and the bars over K and U indicate average values. The kinetic energy Ki of an individual molecule includes contributions due to its rotation and vibration, as well as its translational energy miv2i /2 where vi is the molecule’s speed measured relative to the centre of mass of the system. The potential energy Ui is associated only with the interactions between molecule i and the other molecules of the system. In fact, neither the system’s location nor its motion is of any consequence as far as the internal energy is concerned.

In an ideal monatomic gas, each molecule is a single atom. Consequently, there is no rotational or vibrational kinetic energy and Ki = miv2i /2. Furthermore, there are no interatomic interactions (collisions notwithstanding), so Ui = constant, which we set to zero. The internal energy is therefore due to translational kinetic energy only and

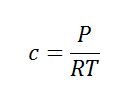
We know that the average kinetic energy of a molecule in an ideal monatomic gas is

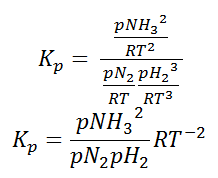
where T is the Kelvin temperature of the gas. Consequently, the average mechanical energy per molecule of an ideal monatomic gas is also 3kBT/2 that is,

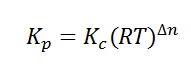
The internal energy is just the number of molecules multiplied by the average mechanical energy per molecule. Thus, for n moles of an ideal monatomic gas,

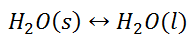
The internal energy for a given quantity of an ideal monatomic gas is totally independent of pressure and volume and depends only on the temperature of the gas, in case of other systems the internal energy cannot be so easily expressed but however the internal energy can often be related to increase in temperature.

When two systems are kept in thermal contact, both eventually reach thermal equilibrium, the point at which both systems are at the same temperature as an example, suppose we mix two monatomic ideal gases. Now, the energy present per molecule of an ideal gas is proportional to its temperature. Therefore, when both the gases are mixed, energy is lost by the molecules that have hotter gas, and in case of colder gas energy is gained, this process continues until equilibrium is reached, at this point the average translational kinetic energy per molecule and the temperature is same for both the gases

Q12) What do you mean by Heat Capacity?

A12) The heat capacity of a substance can be defined as the amount of heat required to change its temperature by one degree.

Thermodynamics in mainly concerned with heat, earlier heat was considered as a measure of an invisible fluid, caloric and present in any matter. The ability of a substance to hold this fluid was earlier referred to as the heat capacity of the system, the meaning however of today is that heat capacity is energy in transit. The development in thermodynamics and dependence of heat transfer on temperature changed the definition of heat.

Modern thermodynamics defines heat as the measure of the total internal energy of a system. In order to quantify the heat energy associated with matter and its dependence on temperature, two properties were defined. These properties were named as specific heat capacity and heat capacity of the system.

Heat Capacity Formula

Mathematically,

Q=CΔT

Where Q is the heat energy required to bring about a temperature change of ΔT and C is the heat capacity of the system under study.

Q13) Derive the relationship between Cp and Cv?

A13) Relation between Cp and Cv

 As the body absorbs heat the temperature of the body rises, but when heat is withdrawn from the body it cools down, so the heat of the body decreases. The temperature of any body is the measure of its molecule’s kinetic energy. Heat capacity is the ratio of heat absorbed by a material to the temperature change. Therefore, the temperature change in a body is directly proportional to the heat transferred to the given body.

Definition of Molar heat capacity

The total amount of energy in the form of heat needed to increase the temperature of 1 mole of any substance by 1 unit is called molar heat capacity(C) of that substance. It also depends greatly on the nature, size and composition of a substance in a system.

 q=n C ΔT

q is the heat supplied or needed to bring about a change in temperature(ΔT) in 1 mole of any given substance.

n is the amount of moles; the constant C is known as the molar heat capacity of the body of the given substance.

Cp: in a system, Cp is the amount of heat energy released or absorbed by a unit mass of the substance with the change in temperature at a constant pressure.in other words, under constant pressure it is the heat energy transfer between a system and the surroundings. So, Cp represents the molar heat capacity, C when pressure is constant. The change in temperature will always cause a change in the enthalpy of the system.

Enthalpy (ΔH) is the heat energy absorbed or released by the system, furthermore enthalpy change occurs during the change of phase or state of a substance.

For example, when a solid change to its liquid form (i.e., the change from ice to water) enthalpy change is called the heat of fusion. When a liquid change to its gaseous form (i.e., the change from water-to-water vapour) the enthalpy change is called the heat of vaporisation.

The system absorbs or releases heat without the change in pressure in that substance, then its specific heat at constant pressure, Cp can be written as:

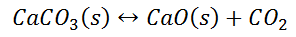……………………….1

Where Cp represents the specific heat at constant pressure; dH is the change in enthalpy; dT is the change in temperature.

Cv: During a small change in the temperature of a substance, Cv is the amount of heat energy absorbed/released per unit mass of a substance, where volume does not change, in other words Cv is the heat energy transfer between a system and its surroundings, without any change in the volume of the system.

Cv represents the molar heat capacity C when the volume is constant. Under a constant volume, the volume of a substance does not change, so the change in volume is zero.

As the term is related to the internal energy of a system, which is total of both potential energy and kinetic energy of that system. The system absorbs or releases heat without change in volume of that substance, then its specific heat at constant volume Cv can be

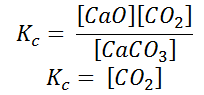 ………………………………….2

Where Cv represents the specific heat at constant volume, dU is the small change in the internal energy of the system; dT is the change in temperature of the systems.

Relationship between Cp and Cv

According to the first law of thermodynamics:

ΔQ= ΔU+ΔW where ΔQ is the amount of heat that is given to the system, ΔU is the internal energy and ΔW is the work done.

Therefore, we write

ΔQ=ΔU+PΔV as ΔW= PΔV……………………………3

Since ΔQ= nCpΔT and ΔU = nvCΔT

Therefore    nCpΔT = nCpΔT + PΔV

We know that PV=nRT)

At T1 kelvin PV1=nRT1………………(.a)

At T2 Kelvin PV2 = nRT2 -----------------(b)

Subtracting (a) from (b)

PV2 – PV1 = n RT2 – nRT1

P(V2-V1) = nR(T2-T1)

Where V2-V1 = ∆V

T2 – T1 = ∆T

Therefore P∆V = n R ∆T

Putting the value of P∆V we get

n Cp ∆T  = n Cv∆T + n R ∆T

n Cp ∆T  = n ∆T (Cv+  R)

Cp = Cv + R

Or Cp – Cv = R

The following relationship can be given considering the ideal gas behaviour of a Gas.

Cp-Cv = R

Where R is the universal gas constant.

Q15) Describe the relation between P-T, P-V. V-T?

A15) We will be deriving the relation between P, V and T using first the law of thermodynamics which states that heat supplied to the system is capable of doing work when heat absorbed by the system is equal to the sum of the increase in internal energy and the external work done on the surrounding by the system.

An essential condition is that

The system and surrounding must not be exchanging heat for which the walls should be insulated.

The process of expansion and compression so that the system should not be able to exchange heat with surroundings.

Relation between P and V

According to First law of thermodynamics

dQ = dU+ dW

For 1 mole of gas

dU= CvdT

dW = PdV

For adiabatic process dQ = 0

dQ =dU+dW

0=Cv dT+P dV

According to ideal Gas equation

PV= RT, differentiating on both sides we get

P dV+ V dP= R dT

K is constant

This Equation gives the relationship between P and V of an ideal gas

Relation between P and T

We know that PV= RT for 1 mole of a gas

Substituting the value of V in the equation

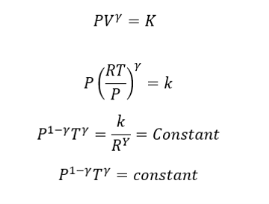
   This equation gives the equation for P and T

Relation between V and T

We know that PV= RT for 1 mole of a gas

P = RT/V

Substituting the value of P in the equation

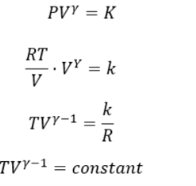
  This equation gives the relation for V and T

Q16) What do you understand by Clausius Inequality, how is it related to Entropy?

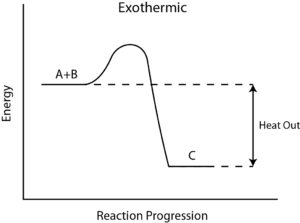
A16) It was Introduced by the German Physicist Rudolf Clausius in 1850, and is a highlight of 19th century Physics. The word “entropy” is derived from the Greek word, which means “turning”. It was derived to provide a quantitative measure for the spontaneous changes and Clausius introduced the concept of entropy as a precise way of expressing the Second Law of Thermodynamics, Clausius form of the second law states that spontaneous change for an irreversible process in an isolated system is a measure of randomness or irregularity or disorder of the system, the more or the randomness, higher is the entropy.

Solid state has the lowest or least entropy, the gaseous state has the highest entropy and the liquid state has the entropy that lies between the two.

Entropy is a state function. The changes in its value during any process, is called the entropy change.

ΔS = S2 -S1 = ∑S products – ∑S reactants 

1) When a system absorbs heat, the molecules begin to move faster because the kinetic energy increases. therefore, disorder increases. Greater the heat absorbed, greater will be the disorder.

2) For equal amount of heat absorbed at low temperature, the disorder will be more than at high temperature. This proves that entropy change is inversely proportional to temperature.

ΔS = eve / T

Entropy change during a process is defined as the quantity of heat (q) absorbed isothermally and reversibly divided by the absolute Temperature (T) at which the heat is absorbed.

The entropy change between two specified states is the same whether the process is reversible or irreversible.

The inequity of the Clausius is a consequence of second law of thermodynamics

Q is he transfer of heat to and from the system

T is the absolute temperature at the boundary, the symbol      is the cyclic integral.

The Clausius inequality for a closed system states that the process is irreversible if TdS > dQ, and the process is reversible if TdS = dQ.

The entropy difference between any two states of a system can be evaluated by the integral of its initial state and final state

Since entropy is a state function, the entropy change of the system for an irreversible path is the same as for a reversible path between the same two states.

For the reversible process the universe is brought back to its initial state without changing its properties. So, the entropy generation for the reversible process is zero. However, for the irreversible process, because of the disorder of the system some entropy is generated. the generated entropy is measure of the irreversibility. As a result of this the cyclic integral of the irreversible process is always less than zero.

Q17) What is the Ionic Product of water?

A17) Ionic product of water

The self-ionization of water deals with the process where the water ionizes to hydroxide ions and hydronium ions, this usually occurs on a limited scale. When two water molecules collide, there is a transfer of hydrogen ion from one molecule to the other. The products formed are hydronium ions that are positively charged and negatively charged hydroxide ions.

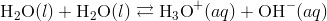
The simplified form of this equation is:

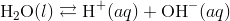
Kw is the ion-product of water symbol. The equilibrium constant for the self-ionization of water is referred to as the ion-product for water.

The ion-product of water 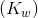  is mathematically the product of the concentration of hydroxide ions and hydrogen ions. Since water is in its pure form, it is not included in the ion-product expression the value of  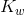 is very small, in accordance with a reaction that favours the reactants. At 25°C, the experimentally determined value of K w in pure water is 1.0 × 10 -14.

In pure water, the concentrations of hydroxide ions and hydrogen ions are equal to one another, in case of pure water or any other aqueous solution, if this ratio exists it is said to be neutral. To find the molarity of each ion, the square root of 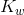  is taken.

An acidic solution, in this solution the concentration of the hydrogen ions is greater than that of the hydroxide ions. For example, hydrogen chloride ionizes to produce H + and Cl − ions upon dissolving in water.

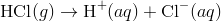
This leads to an increase in the concentration of H + ions in the solution. According to LeChâtelier’s principle, the equilibrium represented

by 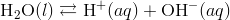 is forced to the left, towards the reactant. As a result, the concentration of the hydroxide ion decreases.

A basic solution, in this solution the concentration of hydroxide ions is greater than the concentration of hydrogen ions. Solid potassium hydroxide dissociates in water to yield potassium ions and hydroxide ions.

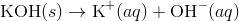
The increase in concentration of the OH − ions causes a decrease in the concentration of the H + ions and the ion-product of [H +] [OH −] remains constant

Q18) What are the dissociation constants of Acids and Bases?

A18) Ka, pKa, Kb, and pKb are very useful to calculate is a particular species will accept or donate protons at a specific pH value. they define the degree of ionization of a base or an acid and they are also true indicators that indicate the strengths of acid and base as adding water to a solution will not change the equilibrium constant. Ka and pKa relate to acids, while Kb and pKb deal with bases. Like pH and pOH, these values also account for hydrogen ion or proton concentration (for Ka and pKa) or hydroxide ion concentration (for Kb and pKb).

Ka and Kb are related to each other through the ion constant for water, Kw:

Kw = Ka x Kb

Ka is dissociation constant for acid and pKa is simply the -log of this constant. Similarly, Kb is the dissociation constant for bases, while pKb is the -log of the constant. The acid and base dissociation constants are usually expressed in terms of moles per liter (mol/L). Acids and bases dissociate according to general equations:

In the formulas, A stands for acid and B for base.

A large Ka value indicates a strong acid because it means the acid is largely dissociated into its ions. A large Ka value also means the formation of products in the reaction is favoured. A small Ka value means little of the acid dissociates, so you have a weak acid. The Ka value for most weak acids ranges from 10-2 to 10-14.

The pKa gives the same information, just in a different way. The smaller the value of pKa, the stronger the acid. Weak acids have a pKa ranging from 2-14

Kb and pKb

Kb is the base dissociation constant. The base dissociation constant is a measure of how completely a base dissociates into its component ions in water.

A large Kb value indicates the high level of dissociation of a strong base. A lower pKb value indicates a stronger base.

pKa and pKb are related by the simple relation:

pKa + pKb = 14

Q19) Define Buffer Index and Buffer capacity?

A19) The Buffer index is defined as the differential ratio that increases due to the addition of the amount of strong acid or strong base to pH variation.

 The buffer capacity on the other hand is expressed numerically and is equal to the minimum concentration of a strong base or a strong acid that brings a variation in the Buffer pH with one unit. The field of application of both notions is different: the buffer capacity is used in the quantitative chemical analysis and the buffer index in studying biological systems.

Buffers are generally characterised by pH range by which they maintain a more or less constant pH by their buffer capacity. the amount of strong acid or base that can be absorbed before the pH changes significantly. Though the pH range of a Buffer solution strongly depends on the chemical properties of the weak acid and weak base used to prepare the buffer (i.e., on KK), its buffer capacity depends solely on the concentrations of the species in the buffered solution. The more concentrated the buffer solution, the greater its buffer capacity.

The buffer solutions usually consist of a weak acid and its conjugate base. When H+ is added to a buffer, the protons (H+) are accepted by the acid’s conjugate base and absorbs the (H+) before the solution pH lowers significantly. Ina similar case, when OH- is added the weak acid donates a proton (H+) to its conjugate base, and thereby resists any increase in pH before shifting to a new equilibrium point. In biological systems, buffers prevent the fluctuation of pH via processes that produce acid or base by-products to maintain an optimal pH.

Q20) Define Common Effect?

A20) The common ion effect is an effect that supresses or subdues the ionization of an electrolyte by another electrolyte (which contains an ion which is also present in the first electrolyte, i.e., a common ion) when it is added. It is considered to be a consequence of Le Chatlier’s principle (or the Equilibrium Law).

The statement of the common ion effect can be written as follows –in a solution, where there are several species interacting with eachother through a chemical equilibrium process, an increase in the concentration of one of the ions that is dissociated in the solution by the addition of another species that contain the same ions leads to an increase in the degree of association of ions.

An example of the common ion effect can be observed when gaseous hydrogen chloride is passed through a sodium chloride solution, leading to the precipitation of the NaCl due to the excess of chloride ions in the solution (brought on by the dissociation of HCl).

This effect cannot be observed in the compounds of transition metals. This is because the d-block elements have a tendency to form complex ions. This can be observed in the compound cuprous chloride, which is insoluble in water. This compound can be dissolved in water by the addition of chloride ions leading to the formation of the CuCl2– complex ion, which is soluble in water.