UNIT 8

BEE

1. Explain 2’s Complement Addition.

Addition in the 2’s complement, it always follows the same rule as it is used in the normally binary addition.

Example- we want to add (8)10 and (-3)10.

First we have to convert them into 2’s complement and simply add them.

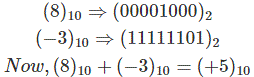
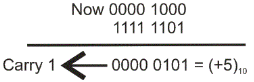
As carry is 1 then number is positive.

Here carry is 1 and it is out of 8 bits hence is not considered in byte and hence the answer is one byte long positive number. So it is clear that for signed and unsigned numbers addition can be performed easily in 2’s complement.

2. Explain 2’s Complement Subtraction.

Subtraction in 2’s complement follows the same rule as it is in the normally binary addition. Only thing is that here subtrahend is first converted to its negative form and then it is added with minuend. Suppose we want to subtract (8)10 from (9)10. First convert (8)10 from (-9)10 into 2’s complement and simply add.

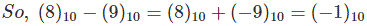
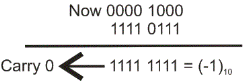
As carry is 0 then number is negative. So it is clear that subtraction can be performed easily in 2’s complement easily.

3 Explain various basic logic gates.

The basic gates are namely AND gate, OR gate & NOT gate.

AND gate

It is a digital circuit that consists of two or more inputs and a single output which is the logical AND of all those inputs. It is represented with the symbol ‘.’.

The following is the truth table of 2-input AND gate.

Here A, B are the inputs and Y is the output of two-input AND gate.

If both inputs are ‘1’, then only the output, Y is ‘1’. For the remaining combinations of inputs, the output, Y is ‘0’.

The figure below shows the symbol of an AND gate, which is having two inputs A, B, and one output, Y.

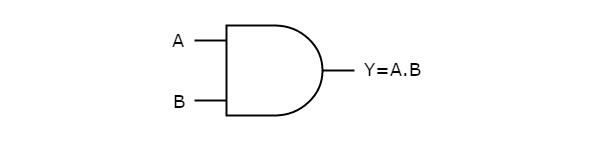
Fig. : AND gate (ref. 1)

Timing Diagram:

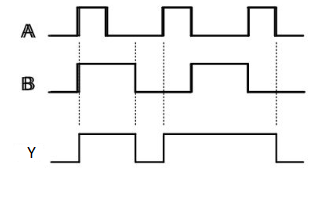
OR gate

It is a digital circuit that has two or more inputs and a single output which is the logical OR of all those inputs. It is represented with the symbol ‘+’.

The truth table of the 2-input OR gate is:

Here A, B are the inputs and Y is the output of two-input OR gate.

When both inputs are ‘0’, then only the output, Y is ‘0’. For remaining combinations of inputs, the output, Y is ‘1’.

The figure below shows the symbol of an OR gate, which is having two inputs A, B, and one output, Y.

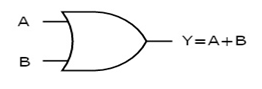
Fig. : OR gate (ref. 1)

Timing Diagram:

NOT gate

It is a digital circuit that has one input and one output. Here the output is the logical inversion of input. Hence, it is also called an inverter.

The truth table of NOT gate is:

Here A and Y are the corresponding input and output of a NOT gate. When A is ‘0’, then, Y is ‘1’. Similarly, when, A is ‘1’, then, Y is ‘0’.

The figure below shows the symbol of NOT gate, which has one input, A and one output, Y.

Fig. : NOT gate (ref. 1)

Timing Diagram:

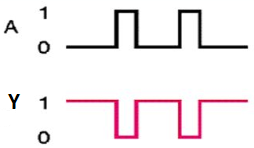
4. Draw and explain Universal gates.

      NAND & NOR gates are known as universal gates.

      We can implement any Boolean function by using NAND gates and NOR gates alone.

NAND gate

It is a digital circuit that has two or more inputs and single output and it is the inversion of logical AND gate.

The truth table of the 2-input NAND gate is:

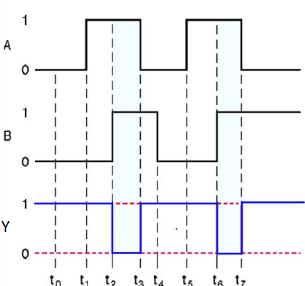
Here A, B are the inputs and Y is the output of two-input NAND gate. When both inputs are ‘1’, then the output, Y is ‘0’. If at least one of the input is zero, then the output, Y is ‘1’. This is just the inverse of AND operation.

The image shows the symbol of NAND gate:

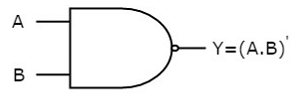
                                              Fig.: NAND gate (ref. 1)

NAND gate works the same as AND gate followed by an inverter.

Timing Diagram:

NOR gate

It is a digital circuit that has two or more inputs and a single output which is the inversion of logical OR of all inputs.

The truth table of 2-input NOR gate is:

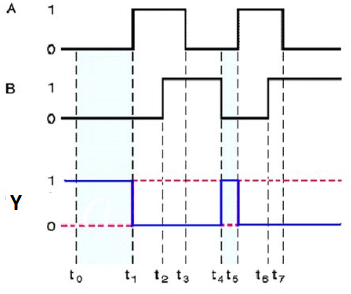
Here A and B are the two inputs and Y is the output. If both inputs are ‘0’, then the output is ‘1’. If anyone of the input is ‘1’, then the output is ‘0’. This is exactly opposite to the two-input OR gate operation.

The symbol of NOR gate is:

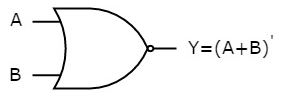
                                                           Fig.: NOR gate (ref. 1)

NOR gate works the same as that of OR gate followed by an inverter.

Timing Diagram:

5.Explain Special Gates in detail.

Ex-OR gate

It stands for the Exclusive-OR gate. Its function varies when the inputs have an even number of ones.

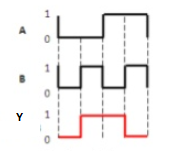
The truth table of the 2-input Ex-OR gate is:

Here A, B are the inputs and Y is the output of two input Ex-OR gate. The output (Y) is zero instead of one when both the inputs are one.

Therefore, the output of the Ex-OR gate is ‘1’, when only one of the two inputs is ‘1’. And it is zero when both inputs are the same.

The symbol of the Ex-OR gate is as follows:

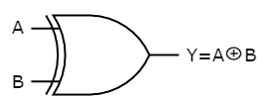
                                                           Fig.: XOR gate (ref. 1)

It is similar to that of the OR gate with an exception for a few combinations (s) of inputs. Hence, the output is also known as an odd function.

Timing Diagram:

Ex-NOR gate

It stands for the Exclusive-NOR gate. Its function is the same as that of the NOR gate except when the inputs having an even number of ones.

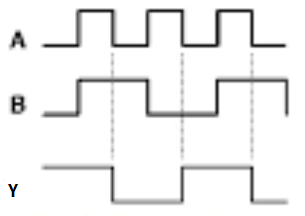
The truth table of the 2-input Ex-NOR gate is:

Here A, B are the inputs and Y is the output. It is the same as the Ex-NOR gate with the only modification in the fourth row. The output is 1 instead of 0 when both the inputs are one.

Hence the output of the Ex-NOR gate is ‘1’ when both inputs are the same and 0 when both the inputs are different.

The symbol of the Ex-NOR gate is:

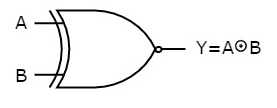
                                       Fig.: XNOR gate (ref. 1)

It is similar to the NOR gate except for a few combinations (s) of inputs. Here the output is ‘1’ when even the number of 1 is present at the inputs. Hence is also called an even function.

Timing Diagram:

6. State and explain De Morgan’s Theorem.

• It is useful in finding the complement of the Boolean function.
• It states that “The complement of logical OR of at least two Boolean variables is equal to the logical AND of each complemented variable”.
• It can be represented using 2 Boolean variables x and y as

(x + y)’ = x’.y’

• The dual of the above Boolean function is

(x.y)’ = x’ + y’

• Therefore, the complement of logical AND of the two Boolean variables is equivalent to the logical OR of each complemented variable.
• Similarly, DeMorgan’s theorem can be applied for more than 2 Boolean variables also.

7.     Simplify the Boolean function,

f = p’qr + pq’r + pqr’ + pqr

Method 1

Given

f = p’qr + pq’r + pqr’ +pqr.

In the first and second terms, r is common and in third and fourth terms pq is common.

So, taking out the common terms by using Distributive lawwe get,

⇒ f = (p’q + pq’)r + pq(r’ + r)

The terms present in the first parenthesis can be simplified by using the Ex-OR operation.

           The terms present in the second parenthesis is equal to ‘1’ using Boolean postulatewe get

⇒ f = (p ⊕q)r + pq(1)

The first term can’t be simplified further.

But, the second term is equal to pq using Boolean postulate.

⇒ f = (p ⊕q)r + pq

Therefore, the simplified Boolean function is f = (p⊕q)r + pq

Method 2

Given f = p’qr + pq’r + pqr’ + pqr.

Using the Boolean postulate, x + x = x.

Hence we can write the last term pqr two more times.

⇒ f = p’qr + pq’r + pqr’ + pqr + pqr + pqr

Now using the Distributive law for 1st and 4th terms, 2nd and 5th terms, 3rdand 6th terms we get.

⇒ f = qr(p’ + p) + pr(q’ + q) + pq(r’ + r)

Using Boolean postulate, x + x’ = 1 and x.1 = x for further simplification.

⇒ f = qr(1) + pr(1) + pq(1)

⇒ f = qr + pr + pq

⇒ f = pq + qr + pr

Therefore, the simplified Boolean function is f = pq + qr + pr.

Hence we got two different Boolean functions after simplification of the given Boolean function. Functionally, these two functions are the same. As per requirement, we can choose one of them.

8 Find the complement of the Boolean function,

f = p’q + pq’.

Solution:

Using DeMorgan’s theorem, (x + y)’ = x’.y’ we get

⇒ f’ = (p’q)’.(pq’)’

Then by second law, (x.y)’ = x’ + y’ we get

⇒ f’ = {(p’)’ + q’}.{p’ + (q’)’}

Then by using, (x’)’=x  we get

⇒ f’ = {p + q’}.{p’ + q}

⇒ f’ = pp’ + pq + p’q’ + qq’

Using x.x’=0 we get

⇒ f = 0 + pq + p’q’ + 0

⇒ f = pq + p’q’

Therefore, the complement of Boolean function, p’q + pq’ is pq + p’q’.

UNIT 8

BEE

1. Explain 2’s Complement Addition.

Addition in the 2’s complement, it always follows the same rule as it is used in the normally binary addition.

Example- we want to add (8)10 and (-3)10.

First we have to convert them into 2’s complement and simply add them.

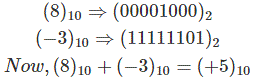
As carry is 1 then number is positive.

Here carry is 1 and it is out of 8 bits hence is not considered in byte and hence the answer is one byte long positive number. So it is clear that for signed and unsigned numbers addition can be performed easily in 2’s complement.

2. Explain 2’s Complement Subtraction.

Subtraction in 2’s complement follows the same rule as it is in the normally binary addition. Only thing is that here subtrahend is first converted to its negative form and then it is added with minuend. Suppose we want to subtract (8)10 from (9)10. First convert (8)10 from (-9)10 into 2’s complement and simply add.

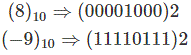
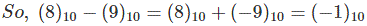
As carry is 0 then number is negative. So it is clear that subtraction can be performed easily in 2’s complement easily.

3 Explain various basic logic gates.

The basic gates are namely AND gate, OR gate & NOT gate.

AND gate

It is a digital circuit that consists of two or more inputs and a single output which is the logical AND of all those inputs. It is represented with the symbol ‘.’.

The following is the truth table of 2-input AND gate.

Here A, B are the inputs and Y is the output of two-input AND gate.

If both inputs are ‘1’, then only the output, Y is ‘1’. For the remaining combinations of inputs, the output, Y is ‘0’.

The figure below shows the symbol of an AND gate, which is having two inputs A, B, and one output, Y.

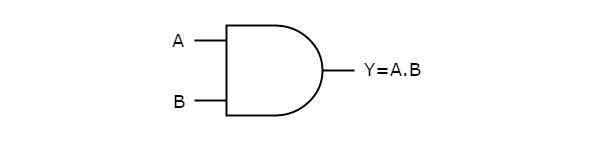
Fig. : AND gate (ref. 1)

Timing Diagram:

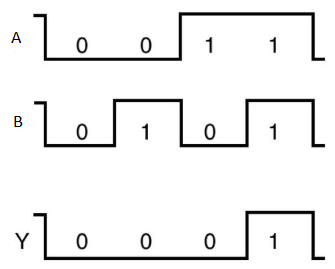
OR gate

It is a digital circuit that has two or more inputs and a single output which is the logical OR of all those inputs. It is represented with the symbol ‘+’.

The truth table of the 2-input OR gate is:

Here A, B are the inputs and Y is the output of two-input OR gate.

When both inputs are ‘0’, then only the output, Y is ‘0’. For remaining combinations of inputs, the output, Y is ‘1’.

The figure below shows the symbol of an OR gate, which is having two inputs A, B, and one output, Y.

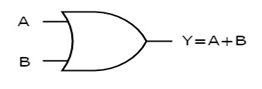
Fig. : OR gate (ref. 1)

Timing Diagram:

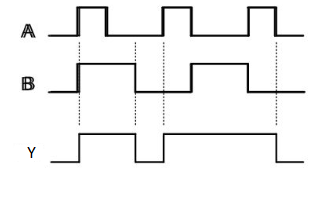
NOT gate

It is a digital circuit that has one input and one output. Here the output is the logical inversion of input. Hence, it is also called an inverter.

The truth table of NOT gate is:

Here A and Y are the corresponding input and output of a NOT gate. When A is ‘0’, then, Y is ‘1’. Similarly, when, A is ‘1’, then, Y is ‘0’.

The figure below shows the symbol of NOT gate, which has one input, A and one output, Y.

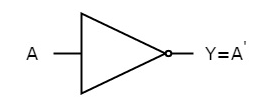
Fig. : NOT gate (ref. 1)

Timing Diagram:

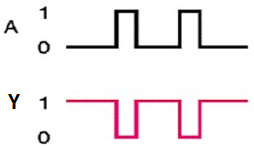
4. Draw and explain Universal gates.

      NAND & NOR gates are known as universal gates.

      We can implement any Boolean function by using NAND gates and NOR gates alone.

NAND gate

It is a digital circuit that has two or more inputs and single output and it is the inversion of logical AND gate.

The truth table of the 2-input NAND gate is:

Here A, B are the inputs and Y is the output of two-input NAND gate. When both inputs are ‘1’, then the output, Y is ‘0’. If at least one of the input is zero, then the output, Y is ‘1’. This is just the inverse of AND operation.

The image shows the symbol of NAND gate:

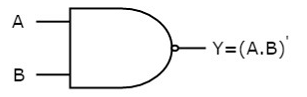
                                              Fig.: NAND gate (ref. 1)

NAND gate works the same as AND gate followed by an inverter.

Timing Diagram:

NOR gate

It is a digital circuit that has two or more inputs and a single output which is the inversion of logical OR of all inputs.

The truth table of 2-input NOR gate is:

Here A and B are the two inputs and Y is the output. If both inputs are ‘0’, then the output is ‘1’. If anyone of the input is ‘1’, then the output is ‘0’. This is exactly opposite to the two-input OR gate operation.

The symbol of NOR gate is:

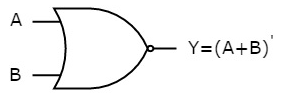
                                                           Fig.: NOR gate (ref. 1)

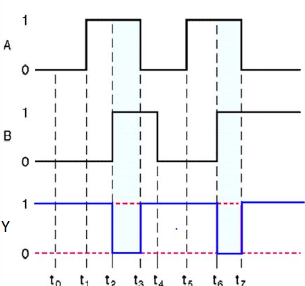
NOR gate works the same as that of OR gate followed by an inverter.

Timing Diagram:

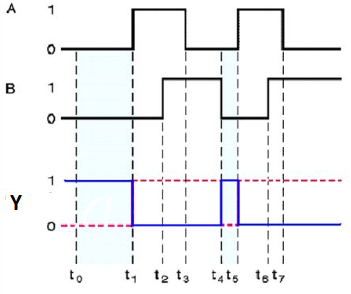
5.Explain Special Gates in detail.

Ex-OR gate

It stands for the Exclusive-OR gate. Its function varies when the inputs have an even number of ones.

The truth table of the 2-input Ex-OR gate is:

Here A, B are the inputs and Y is the output of two input Ex-OR gate. The output (Y) is zero instead of one when both the inputs are one.

Therefore, the output of the Ex-OR gate is ‘1’, when only one of the two inputs is ‘1’. And it is zero when both inputs are the same.

The symbol of the Ex-OR gate is as follows:

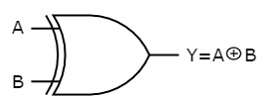
                                                           Fig.: XOR gate (ref. 1)

It is similar to that of the OR gate with an exception for a few combinations (s) of inputs. Hence, the output is also known as an odd function.

Timing Diagram:

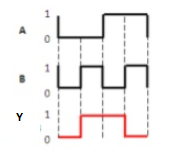
Ex-NOR gate

It stands for the Exclusive-NOR gate. Its function is the same as that of the NOR gate except when the inputs having an even number of ones.

The truth table of the 2-input Ex-NOR gate is:

Here A, B are the inputs and Y is the output. It is the same as the Ex-NOR gate with the only modification in the fourth row. The output is 1 instead of 0 when both the inputs are one.

Hence the output of the Ex-NOR gate is ‘1’ when both inputs are the same and 0 when both the inputs are different.

The symbol of the Ex-NOR gate is:

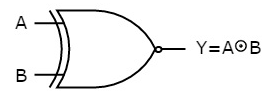
                                       Fig.: XNOR gate (ref. 1)

It is similar to the NOR gate except for a few combinations (s) of inputs. Here the output is ‘1’ when even the number of 1 is present at the inputs. Hence is also called an even function.

Timing Diagram:

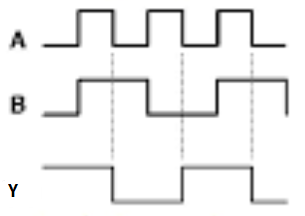
6. State and explain De Morgan’s Theorem.

• It is useful in finding the complement of the Boolean function.
• It states that “The complement of logical OR of at least two Boolean variables is equal to the logical AND of each complemented variable”.
• It can be represented using 2 Boolean variables x and y as

(x + y)’ = x’.y’

• The dual of the above Boolean function is

(x.y)’ = x’ + y’

• Therefore, the complement of logical AND of the two Boolean variables is equivalent to the logical OR of each complemented variable.
• Similarly, DeMorgan’s theorem can be applied for more than 2 Boolean variables also.

7.     Simplify the Boolean function,

f = p’qr + pq’r + pqr’ + pqr

Method 1

Given

f = p’qr + pq’r + pqr’ +pqr.

In the first and second terms, r is common and in third and fourth terms pq is common.

So, taking out the common terms by using Distributive lawwe get,

⇒ f = (p’q + pq’)r + pq(r’ + r)

The terms present in the first parenthesis can be simplified by using the Ex-OR operation.

           The terms present in the second parenthesis is equal to ‘1’ using Boolean postulatewe get

⇒ f = (p ⊕q)r + pq(1)

The first term can’t be simplified further.

But, the second term is equal to pq using Boolean postulate.

⇒ f = (p ⊕q)r + pq

Therefore, the simplified Boolean function is f = (p⊕q)r + pq

Method 2

Given f = p’qr + pq’r + pqr’ + pqr.

Using the Boolean postulate, x + x = x.

Hence we can write the last term pqr two more times.

⇒ f = p’qr + pq’r + pqr’ + pqr + pqr + pqr

Now using the Distributive law for 1st and 4th terms, 2nd and 5th terms, 3rdand 6th terms we get.

⇒ f = qr(p’ + p) + pr(q’ + q) + pq(r’ + r)

Using Boolean postulate, x + x’ = 1 and x.1 = x for further simplification.

⇒ f = qr(1) + pr(1) + pq(1)

⇒ f = qr + pr + pq

⇒ f = pq + qr + pr

Therefore, the simplified Boolean function is f = pq + qr + pr.

Hence we got two different Boolean functions after simplification of the given Boolean function. Functionally, these two functions are the same. As per requirement, we can choose one of them.

8 Find the complement of the Boolean function,

f = p’q + pq’.

Solution:

Using DeMorgan’s theorem, (x + y)’ = x’.y’ we get

⇒ f’ = (p’q)’.(pq’)’

Then by second law, (x.y)’ = x’ + y’ we get

⇒ f’ = {(p’)’ + q’}.{p’ + (q’)’}

Then by using, (x’)’=x  we get

⇒ f’ = {p + q’}.{p’ + q}

⇒ f’ = pp’ + pq + p’q’ + qq’

Using x.x’=0 we get

⇒ f = 0 + pq + p’q’ + 0

⇒ f = pq + p’q’

Therefore, the complement of Boolean function, p’q + pq’ is pq + p’q’.