Unit-1

Successive Differentiation and Mean Value Theorem

Question-1: If y = l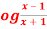 , then show that-

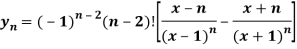
Sol. We have,

              y =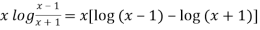

Differentiate y with respect to x, we get

    =

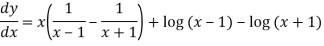
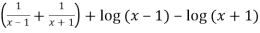
Again diff. (n – 1) times w.r .t x , we get-

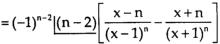
Question-2: Find the derivative of

Sol. Here we have-

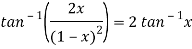
Suppose,   y =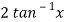

First derivative-

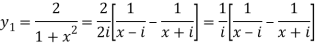
Here ,

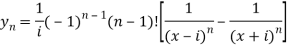
Let x =

So that

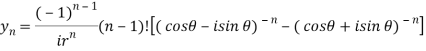
Which is the n’th derivative of the given function.

Question-3: Find cos x cos 2x cos 3x.

Sol.

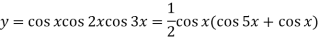
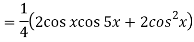
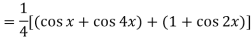
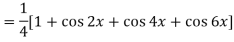
So that-

n’th derivative-

Question-4: Find the 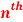derivative of the following function-

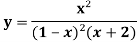
Sol.  Partial fraction of the function y after splitting-

        Suppose x – 1 = z, then

           =

          =

      =

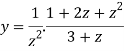
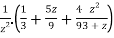
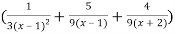
Here we can find its n’th derivative-

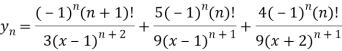
Question-5: Find if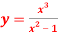

Sol.

Here we have-

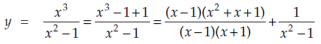
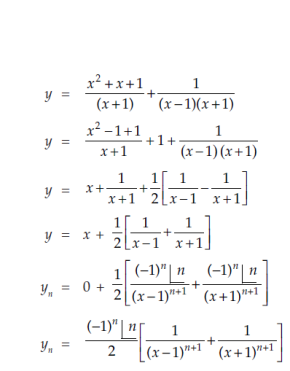
At x = 0,

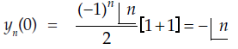
When n is odd-

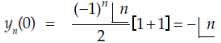
When n is even

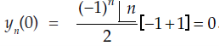
Question-6: If   y 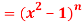 , then prove that-

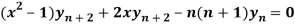
Sol. Here it is given that-

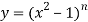
On differentiating-

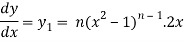
Or

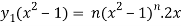
                  = ny.2x

Differentiate again with respect to x, we get-

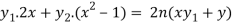
Or

   …………………. (1)

Differentiate each term of (1) by using Leibnitz’s theorem, we get-

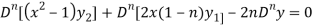
Therefore we get-

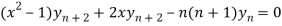
                                                                                                              Hence proved.

Question-7: If 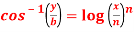, then prove that-

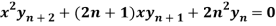
Sol. Here we have-

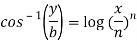
Or

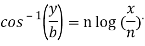
Or

                 y = b cos[ n log(x/n)]              

On differentiating, we get-

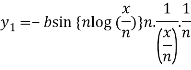
Which becomes-

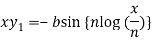
Differentiate again both sides with respect to x, we get-

It becomes-

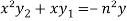
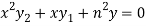       ……………….. (1)

Differentiate each term n times with respect to x, we get-

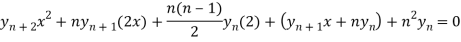
Which is-

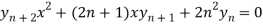hence proved,

Question-8: If ,     then show that

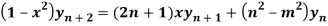
Sol.

Also, find 

Here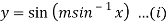

Differentiating with respect to x, we get

   …(ii)

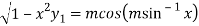
Squaring   both  side  we get

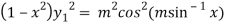
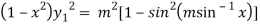
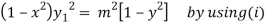
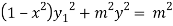   …(iii)

Again differentiating with  respect to  x ,we get

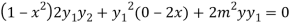
Using Leibnitz’s  theorem  we  get

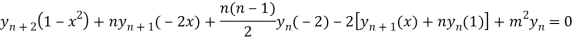
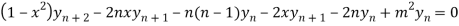
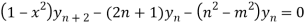        …(iv)

      Putting x=0  in equation (i),(ii) and (iii)  we get

      Putting  n=1,2,3,4….

      ………………

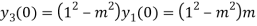
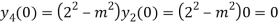
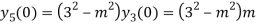
   Hence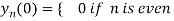   

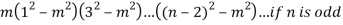
Qustion-9: Verify Rolle’s theorem for the function f(x) = x2 for

Solution:

Here f(x) = x2;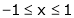

i)      Since f(x) is algebraic polynomial which is continuous in [-1, 1]

Ii)    Consider f(x) = x2

Diff. w.r.t. x we get

f'(x) = 2x

Clearly f’(x) exists in (-1, 1) and does not becomes infinite.

Iii)  Clearly

f(-1) = (-1)2 = 1

f(1) = (1)2 = 1

f(-1) = f(1).

Hence by Rolle ’s Theorem, there exist such that

f’(c) = 0

i.e. 2c = 0

c = 0

Thus 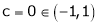such that

f'(c) = 0

Hence Rolle’s Theorem is verified.

Question-10: Verify the Lagrange’s mean value theorem for

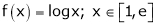
Solution:

Here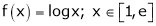

i)      Clearly f(x) = log x is logarithmic function. Hence it is continuous in [1, e]

Ii)    Consider f(x) = log x.

Diff. w.r.t. x we get,

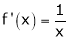
Clearly f’(x) exists for each value of & is finite.

Hence all conditions of LMVT are satisfied Hence at least

Such that

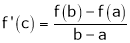
i.e.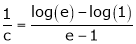

i.e.

i.e.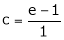

i.e.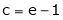

Since e = 2.7183

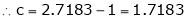
Clearly c = 1.7183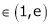

Hence LMVT is verified.

Questin-11: Verify Cauchy mean value theorems for &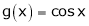in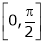

Solution:

Let &;

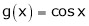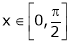
i)      Clearly f(x) and g(x) both are trigonometric functions. Hence continuous in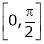

Ii)    Since &

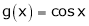
Diff. w.r.t. x we get,

&

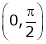Clearly both f’(x) and g’(x) exist & finite in . Hence f(x) and g(x) is derivable in and

Iii)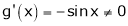 

Hence by Cauchy mean value theorem, there exist at least 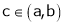such that

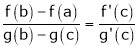
i.e.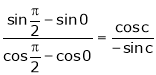

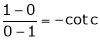
i.e. 1 = cot c

i.e.

Clearly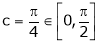

Hence Cauchy mean value theorem is verified.

Question-12: Verify Cauchy’s mean value theorem for the function f(x) = x⁴ and g(x) = x² in the interval [1,2]

Sol. We are given, f(x) = x⁴ and g(x) = x

Derivative of these fucntions ,

      f’(x) = 4x³ and g’(x) = 2x

Put these values in Cauchy’s formula, we get

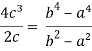
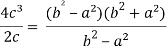
2c² =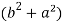

c² =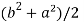

c =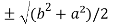

Now put the values of a = 1 and b = 2 ,we get

c = = =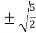 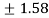(approx..)

Hence the Cauchy’s theorem is verified.

Unit-1

Successive Differentiation and Mean Value Theorem

Question-1: If y = l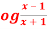 , then show that-

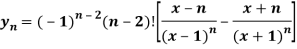
Sol. We have,

              y =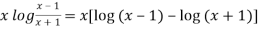

Differentiate y with respect to x, we get

    =

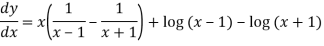
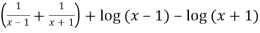
Again diff. (n – 1) times w.r .t x , we get-

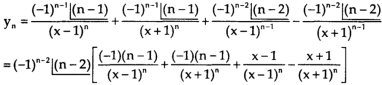
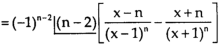
Question-2: Find the derivative of

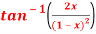
Sol. Here we have-

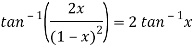
Suppose,   y =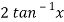

First derivative-

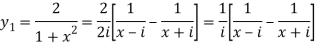
Here ,

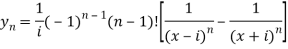
Let x =

So that

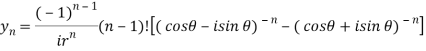
Which is the n’th derivative of the given function.

Question-3: Find cos x cos 2x cos 3x.

Sol.

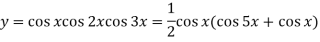
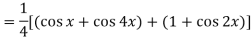
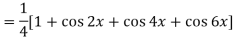
So that-

n’th derivative-

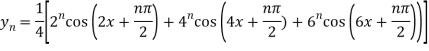
Question-4: Find the derivative of the following function-

Sol.  Partial fraction of the function y after splitting-

        Suppose x – 1 = z, then

           =

          =

      =

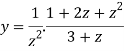
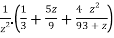
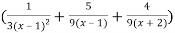
Here we can find its n’th derivative-

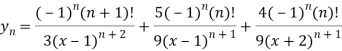
Question-5: Find 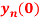if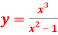

Sol.

Here we have-

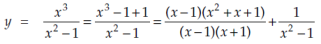
At x = 0,

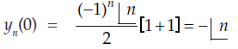
When n is odd-

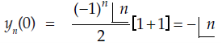
When n is even

Question-6: If   y 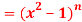 , then prove that-

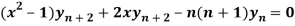
Sol. Here it is given that-

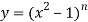
On differentiating-

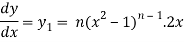
Or

                  = ny.2x

Differentiate again with respect to x, we get-

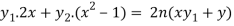
Or

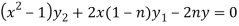   …………………. (1)

Differentiate each term of (1) by using Leibnitz’s theorem, we get-

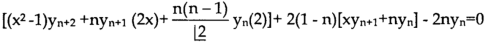
Therefore we get-

                                                                                                              Hence proved.

Question-7: If 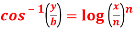, then prove that-

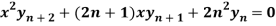
Sol. Here we have-

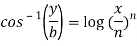
Or

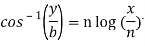
Or

                 y = b cos[ n log(x/n)]              

On differentiating, we get-

Which becomes-

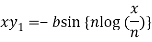
Differentiate again both sides with respect to x, we get-

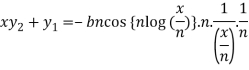
It becomes-

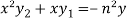
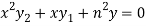       ……………….. (1)

Differentiate each term n times with respect to x, we get-

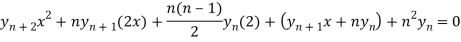
Which is-

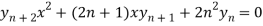hence proved,

Question-8: If ,     then show that

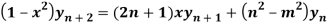
Sol.

Also, find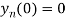 

Here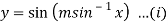

Differentiating with respect to x, we get

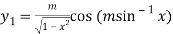   …(ii)

Squaring   both  side  we get

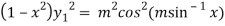
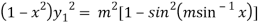
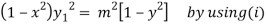
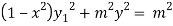   …(iii)

Again differentiating with  respect to  x ,we get

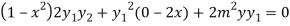
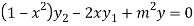
Using Leibnitz’s  theorem  we  get

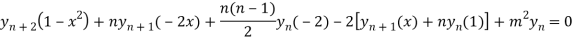
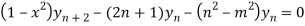        …(iv)

      Putting x=0  in equation (i),(ii) and (iii)  we get

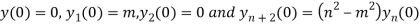
      Putting  n=1,2,3,4….

      ………………

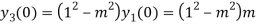
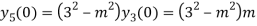
   Hence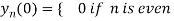   

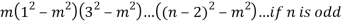
Qustion-9: Verify Rolle’s theorem for the function f(x) = x2 for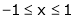

Solution:

Here f(x) = x2;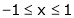

i)      Since f(x) is algebraic polynomial which is continuous in [-1, 1]

Ii)    Consider f(x) = x2

Diff. w.r.t. x we get

f'(x) = 2x

Clearly f’(x) exists in (-1, 1) and does not becomes infinite.

Iii)  Clearly

f(-1) = (-1)2 = 1

f(1) = (1)2 = 1

f(-1) = f(1).

Hence by Rolle ’s Theorem, there exist such that

f’(c) = 0

i.e. 2c = 0

c = 0

Thus 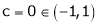such that

f'(c) = 0

Hence Rolle’s Theorem is verified.

Question-10: Verify the Lagrange’s mean value theorem for

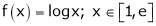
Solution:

Here

i)      Clearly f(x) = log x is logarithmic function. Hence it is continuous in [1, e]

Ii)    Consider f(x) = log x.

Diff. w.r.t. x we get,

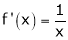
Clearly f’(x) exists for each value of 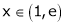& is finite.

Hence all conditions of LMVT are satisfied Hence at least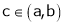

Such that

i.e.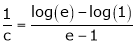

i.e.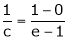

i.e.

i.e.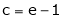

Since e = 2.7183

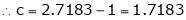
Clearly c = 1.7183

Hence LMVT is verified.

Questin-11: Verify Cauchy mean value theorems for 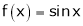&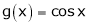in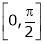

Solution:

Let &;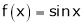

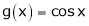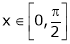
i)      Clearly f(x) and g(x) both are trigonometric functions. Hence continuous in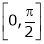

Ii)    Since &

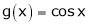
Diff. w.r.t. x we get,

&

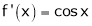Clearly both f’(x) and g’(x) exist & finite in 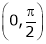. Hence f(x) and g(x) is derivable in 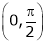and

Iii)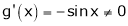 

Hence by Cauchy mean value theorem, there exist at least 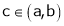such that

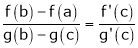
i.e.

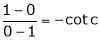
i.e. 1 = cot c

i.e.

Clearly

Hence Cauchy mean value theorem is verified.

Question-12: Verify Cauchy’s mean value theorem for the function f(x) = x⁴ and g(x) = x² in the interval [1,2]

Sol. We are given, f(x) = x⁴ and g(x) = x

Derivative of these fucntions ,

      f’(x) = 4x³ and g’(x) = 2x

Put these values in Cauchy’s formula, we get

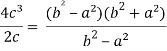
2c² =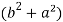

c² =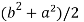

c =

Now put the values of a = 1 and b = 2 ,we get

c = 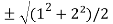= =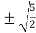 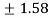(approx..)

Hence the Cauchy’s theorem is verified.