Unit-2

Expansion of Functions and Indeterminate forms

Question-1: By using Maclaurin’s series expand tan x.

Sol.

Let-

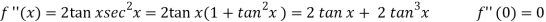
Put these values in Maclaurin’s series we get-

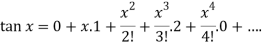
Question-2: Expand by using Maclaurin’s series.

Sol.

Let

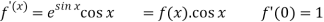
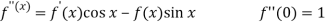
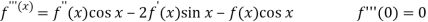
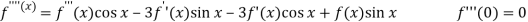
Put these values in Maclaurin’s series-

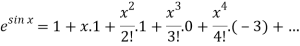
Or

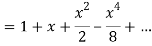
Question-3: Prove that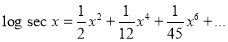

Solution:

Let

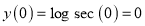
Differentiate with respect to x,

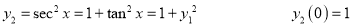
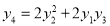
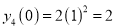
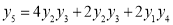
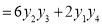
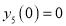
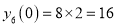
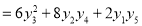
Hence by Maclaurin’s Series,

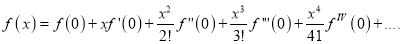
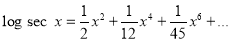
Question-4: Expand by upto.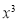

Solution:

We have,

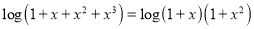
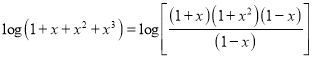
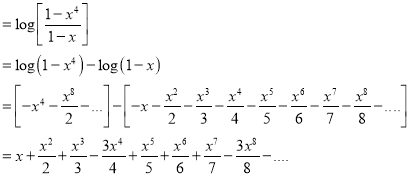
Question-5: Differentiate the function f(x) = 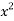by using the first principal method.

Sol.

We know that-

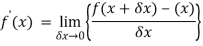
Here

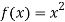
Substituting ( for x gives-

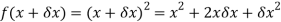
Hence-

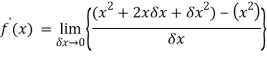
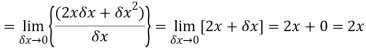
Question-6: Differentiate with respect to x-

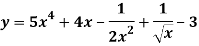
Sol.

The given function can be written in the form

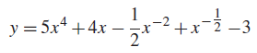
Now-

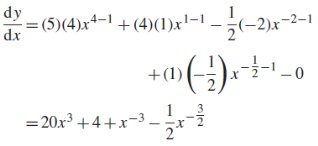
Question-:7 Expand 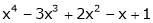in power of (x – 3)

Solution:

Let

Here a = 3

Now by Taylor’s series expansion,

… (1)

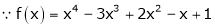
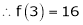
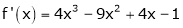
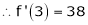
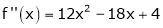
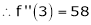
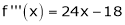
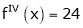
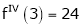
equation (1) becomes.

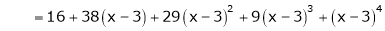
Question-8: Using Taylors series method expand in powers of (x + 2)

Solution:

Here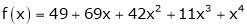

a = -2

By Taylors series,

… (1)

Since

,, …..

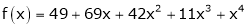
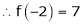
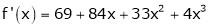
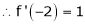
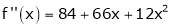
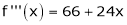
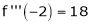
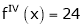
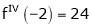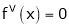Thus equation (1) becomes

Question-9: Expand 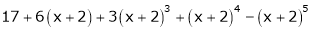in powers of x using Taylor’s theorem,

Solution:

Here

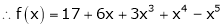
i.e.

Here

h = 2

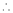By Taylors series

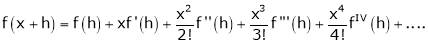… (1)

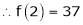
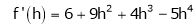
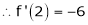
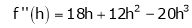
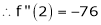
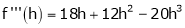
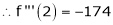
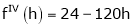
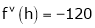
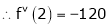
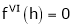
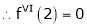
By equation (1)

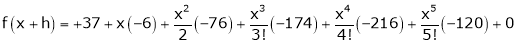
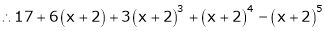
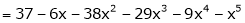
Question-10: Evaluate .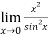

Sol. Let f(x) = 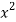and g(x) = .

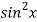Here we see that this is the indeterminate form of 0/0 at x = 0.

Now by using L’Hospital rule, we get-

                                                        =

=

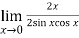
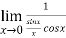
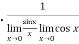                                                       = = 1

Question-11: Evaluate

Sol. We can see that this is an indeterminate form of type 0/0.

Apply L’Hospital’s rule, we get

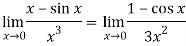
But this is again an indeterminate form, so that we will again apply L’Hospital’s rule-

We get

=

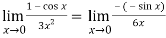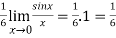
Question-12: Evaluate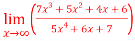

Sol. Apply L’Hospital rule as we can see that this is the form of

=

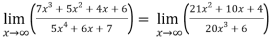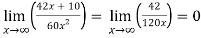
Note- In some cases like above example, we can not apply L’Hospital’s rule.

Unit-2

Expansion of Functions and Indeterminate forms

Question-1: By using Maclaurin’s series expand tan x.

Sol.

Let-

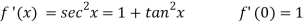
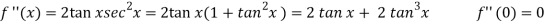
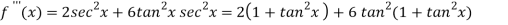
Put these values in Maclaurin’s series we get-

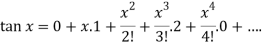
Question-2: Expand 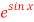by using Maclaurin’s series.

Sol.

Let

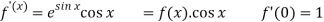
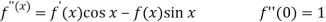
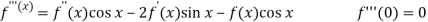
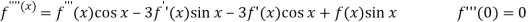
Put these values in Maclaurin’s series-

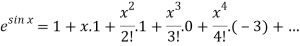
Or

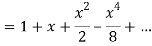
Question-3: Prove that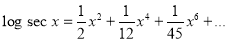

Solution:

Let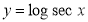

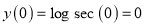
Differentiate with respect to x,

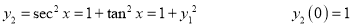
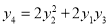
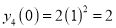
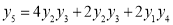
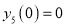
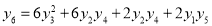
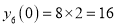
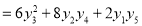
Hence by Maclaurin’s Series,

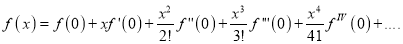
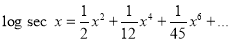
Question-4: Expand by 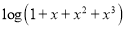upto.

Solution:

We have,

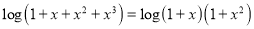
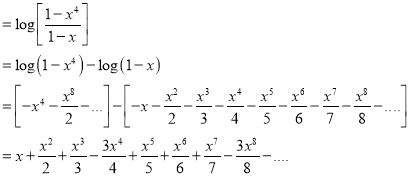
Question-5: Differentiate the function f(x) = 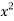by using the first principal method.

Sol.

We know that-

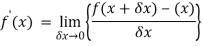
Here

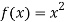
Substituting (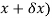 for x gives-

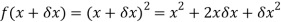
Hence-

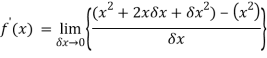
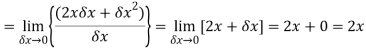
Question-6: Differentiate with respect to x-

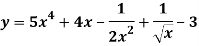
Sol.

The given function can be written in the form

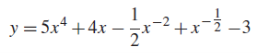
Now-

Question-:7 Expand 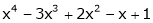in power of (x – 3)

Solution:

Let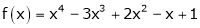

Here a = 3

Now by Taylor’s series expansion,

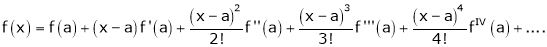… (1)

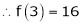
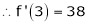
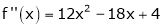
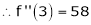
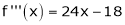
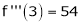
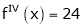
equation (1) becomes.

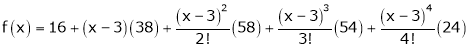
Question-8: Using Taylors series method expand 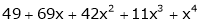in powers of (x + 2)

Solution:

Here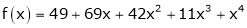

a = -2

By Taylors series,

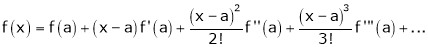… (1)

Since

,, …..

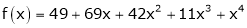
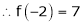
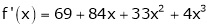
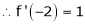
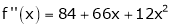
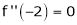
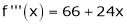
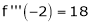
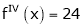
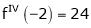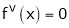Thus equation (1) becomes

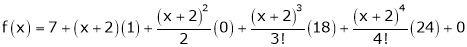
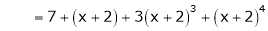
Question-9: Expand 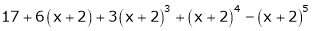in powers of x using Taylor’s theorem,

Solution:

Here

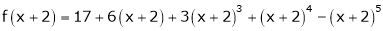
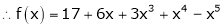
i.e.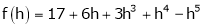

Here

h = 2

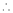By Taylors series

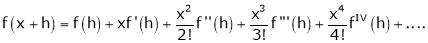… (1)

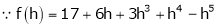
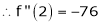
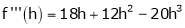
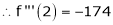
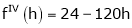
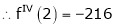
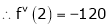
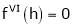
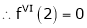
By equation (1)

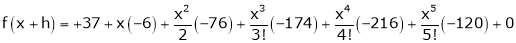
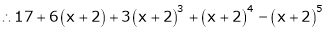
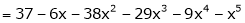
Question-10: Evaluate .

Sol. Let f(x) = 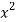and g(x) = .

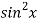Here we see that this is the indeterminate form of 0/0 at x = 0.

Now by using L’Hospital rule, we get-

                                                        =

=

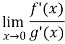
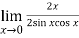
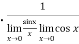                                                       = = 1

Question-11: Evaluate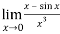

Sol. We can see that this is an indeterminate form of type 0/0.

Apply L’Hospital’s rule, we get

But this is again an indeterminate form, so that we will again apply L’Hospital’s rule-

We get

=

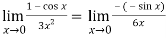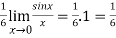
Question-12: Evaluate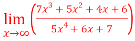

Sol. Apply L’Hospital rule as we can see that this is the form of

=

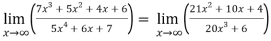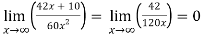
Note- In some cases like above example, we can not apply L’Hospital’s rule.