Unit-5
Applications of Multivariable Differential Calculus
Question-1: If x = r sin , y = r sin
, y = r sin , z = r cos
, z = r cos , then show that
, then show that
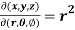 sin
sin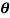 also find
also find 
Sol. We know that,
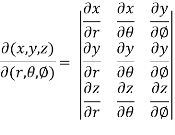
= 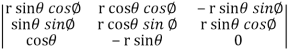
= 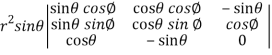
= 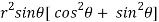 ( on solving the determinant)
( on solving the determinant)
= 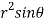
Now using first propert of Jacobians, we get

Question-2: If u = x + y + z ,uv = y + z , uvw = z , find 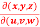
Sol. Here we have,
x = u – uv = u(1-v)
y = uv – uvw = uv( 1- w)
And z = uvw
So that,
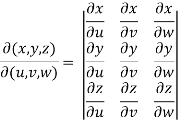
=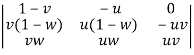
Apply 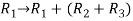
=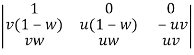
Now we get,
= u²v(1-w) + u²vw
= u²v
Question-3: If u = xyz , v = x² + y² + z² and w = x + y + z, then find J = 
Sol. Here u ,v and w are explicitly given , so that first we calculate
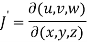
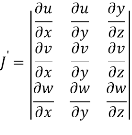
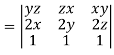
= yz(2y-2z) – zx(2x – 2z) + xy (2x – 2y)
= 2[yz(y-z)-zx(x-z)+xy(x-y)]
= 2[x²y - x²z - xy² + xz² + y²z - yz²]
= 2[x²(y-z) - x(y² - z²) + yz (y – z)]
= 2(y – z)(z – x)(y – x)
= -2(x – y)(y – z)(z – x)
By the property,
JJ’ = 1
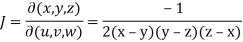
Question-4: If u = 2axy, v = 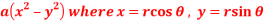 then prove that-
then prove that-
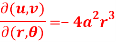
Sol. Here we have,
u = 2axy, v = 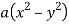
Then
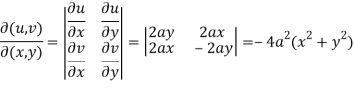
Here - 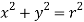
So that
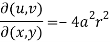
Now,
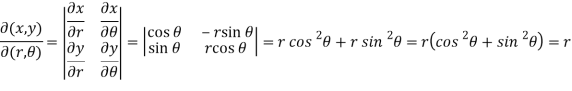
Hence-
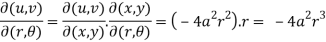
Hence proved.
Question-5: If x + y + z = u, y + z = uv , z = uvw, then prove that-
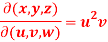
Sol. Suppose
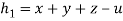
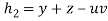
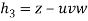
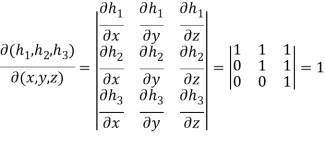
And

Hence,
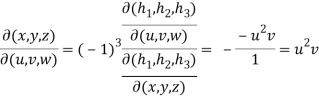
Hence proved.
Question-6: Show that 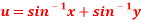 and
and 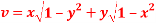 are functionally dependent.
are functionally dependent.
Sol. Here we have-
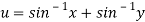 and
and
Now we will find out the Jacobian to check the functional dependence.
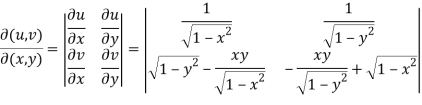
= 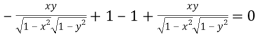
Here Jacobian is zero, so we can conclude that these functions are functionally dependent.
Question-7: Prove that u, v, w are functionally dependent, where-

Sol. Here we have
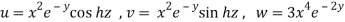
Now we will find out the Jacobian of the given functions-

= 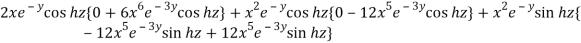
= 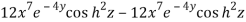
= 0
Therefore, u, v, w are functionally dependent.
Question-8: Find the percentage error in the area of an ellipse where error of ly is made in measuring it’s major and minor axes.
Solution:
Let A be the area of an ellipse and ‘a’ & ‘b’ are its semi major and minor axes

Taking log on both sides.
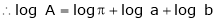
Differentiating we get,

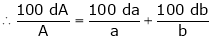


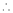 Percentage error ion the area of an ellipse = 2%
Percentage error ion the area of an ellipse = 2%
Question-9: Find out the maxima and minima of the function
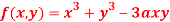
Sol.
Given
 …(i)
…(i)
Partially differentiating (i) with respect to x we get
 ….(ii)
….(ii)
Partially differentiating (i) with respect to y we get
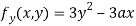 ….(iii)
….(iii)
Now, form the equations 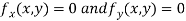
Using (ii) and (iii) we get
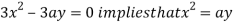
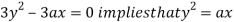
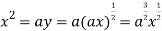 using above two equations
using above two equations
Squaring both side we get
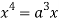
Or 
This show that 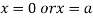
Also we get 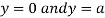
Thus we get the pair of value as 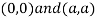
Now, we calculate
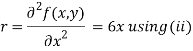
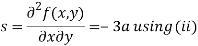
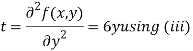
Putting above values in
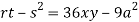
At point (0,0) we get

So, the point (0,0) is a saddle point.
At point 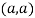 we get
we get
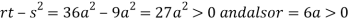
So the point 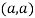 is the minimum point where
is the minimum point where 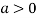
In case 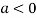
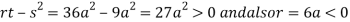
So the point  is the maximum point where
is the maximum point where 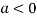
Question-10: Determine the maxima and minima of  when
when 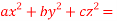 1
1
Sol. Suppose  ……….. (1)
……….. (1)
And 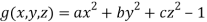 =0 …………… (2)
=0 …………… (2)
Differentiate partially equation (1) and (2) w.r.t. x and y respectively, we get-
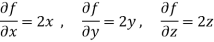
And 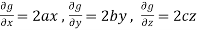
Now using Lagrange’s equations, we get-
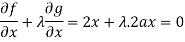
Which gives-
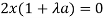 or
or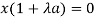 ……… (3)
……… (3)
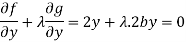
Which gives-
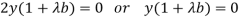 …… (4)
…… (4)
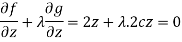
Which gives-
 ……. (5)
……. (5)
Multiply these equations by x, y, z respectively and adding, we get-
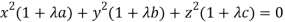
(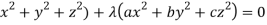
Hence we get-
f + 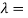 0 then
0 then 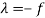
Put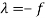 in (3) , (4) and (5), we get-
in (3) , (4) and (5), we get-
x(1 – fa) = 0 , y(1 – fb) = 0 and z(1 – fc) = 0
We get-
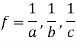
These gives the maximum and minimum values of f.
Question-11: Divide 24 into three parts such that the continued product of the first, square of second and cube of third may be maximum.
Let first number be x, second be y and third be z.
According to the question
Let the given function be f
And the relation 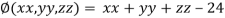
By Lagrange’s Method
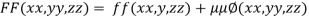
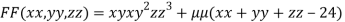 ….(i)
….(i)
Partially differentiating (i) with respect to x,y and z and equate them to zero
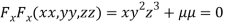 ….(ii)
….(ii)
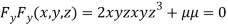 ….(iii)
….(iii)
 ….(iv)
….(iv)
From (ii),(iii) and (iv) we get
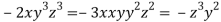
On solving
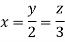
Putting it in given relation we get
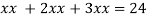
Or 
Or 
Thus the first number is 4 second is 8 and third is 12
Unit-5
Applications of Multivariable Differential Calculus
Question-1: If x = r sin , y = r sin
, y = r sin , z = r cos
, z = r cos , then show that
, then show that
 sin
sin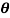 also find
also find 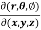
Sol. We know that,
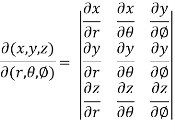
= 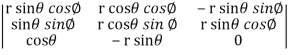
= 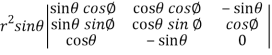
= 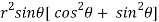 ( on solving the determinant)
( on solving the determinant)
= 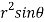
Now using first propert of Jacobians, we get
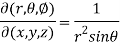
Question-2: If u = x + y + z ,uv = y + z , uvw = z , find 
Sol. Here we have,
x = u – uv = u(1-v)
y = uv – uvw = uv( 1- w)
And z = uvw
So that,
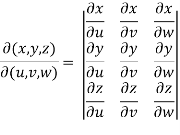
=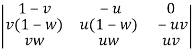
Apply 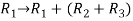
=
Now we get,
= u²v(1-w) + u²vw
= u²v
Question-3: If u = xyz , v = x² + y² + z² and w = x + y + z, then find J = 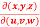
Sol. Here u ,v and w are explicitly given , so that first we calculate
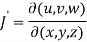
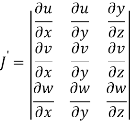
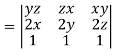
= yz(2y-2z) – zx(2x – 2z) + xy (2x – 2y)
= 2[yz(y-z)-zx(x-z)+xy(x-y)]
= 2[x²y - x²z - xy² + xz² + y²z - yz²]
= 2[x²(y-z) - x(y² - z²) + yz (y – z)]
= 2(y – z)(z – x)(y – x)
= -2(x – y)(y – z)(z – x)
By the property,
JJ’ = 1
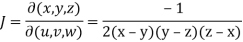
Question-4: If u = 2axy, v = 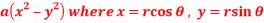 then prove that-
then prove that-
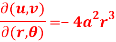
Sol. Here we have,
u = 2axy, v = 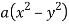
Then
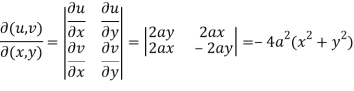
Here - 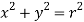
So that
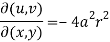
Now,
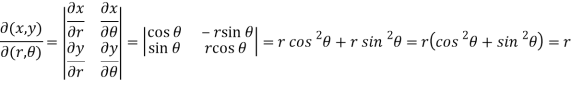
Hence-
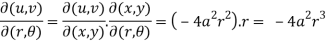
Hence proved.
Question-5: If x + y + z = u, y + z = uv , z = uvw, then prove that-
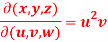
Sol. Suppose
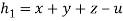

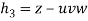
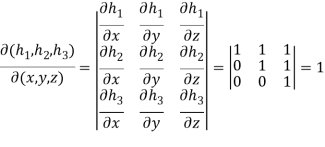
And
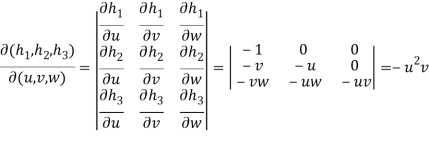
Hence,
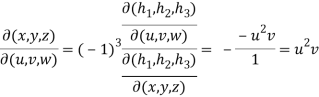
Hence proved.
Question-6: Show that 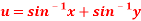 and
and 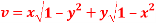 are functionally dependent.
are functionally dependent.
Sol. Here we have-
 and
and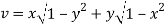
Now we will find out the Jacobian to check the functional dependence.
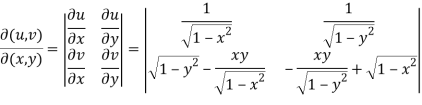
= 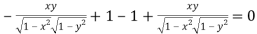
Here Jacobian is zero, so we can conclude that these functions are functionally dependent.
Question-7: Prove that u, v, w are functionally dependent, where-

Sol. Here we have
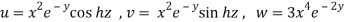
Now we will find out the Jacobian of the given functions-
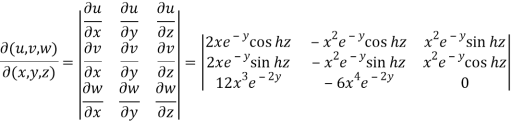
= 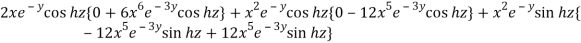
= 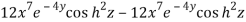
= 0
Therefore, u, v, w are functionally dependent.
Question-8: Find the percentage error in the area of an ellipse where error of ly is made in measuring it’s major and minor axes.
Solution:
Let A be the area of an ellipse and ‘a’ & ‘b’ are its semi major and minor axes
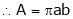
Taking log on both sides.
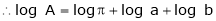
Differentiating we get,

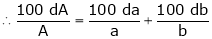


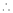 Percentage error ion the area of an ellipse = 2%
Percentage error ion the area of an ellipse = 2%
Question-9: Find out the maxima and minima of the function
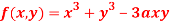
Sol.
Given
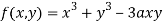 …(i)
…(i)
Partially differentiating (i) with respect to x we get
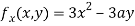 ….(ii)
….(ii)
Partially differentiating (i) with respect to y we get
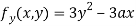 ….(iii)
….(iii)
Now, form the equations 
Using (ii) and (iii) we get

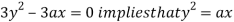
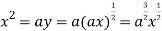 using above two equations
using above two equations
Squaring both side we get
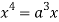
Or 
This show that 
Also we get 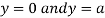
Thus we get the pair of value as 
Now, we calculate
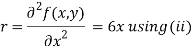
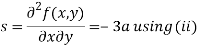
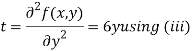
Putting above values in
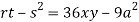
At point (0,0) we get
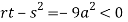
So, the point (0,0) is a saddle point.
At point  we get
we get
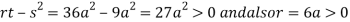
So the point 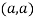 is the minimum point where
is the minimum point where 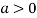
In case 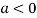
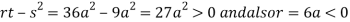
So the point  is the maximum point where
is the maximum point where 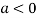
Question-10: Determine the maxima and minima of 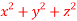 when
when  1
1
Sol. Suppose  ……….. (1)
……….. (1)
And 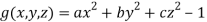 =0 …………… (2)
=0 …………… (2)
Differentiate partially equation (1) and (2) w.r.t. x and y respectively, we get-
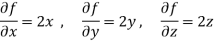
And 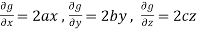
Now using Lagrange’s equations, we get-
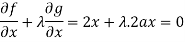
Which gives-
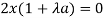 or
or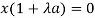 ……… (3)
……… (3)
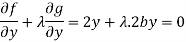
Which gives-
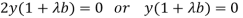 …… (4)
…… (4)
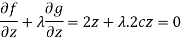
Which gives-
 ……. (5)
……. (5)
Multiply these equations by x, y, z respectively and adding, we get-
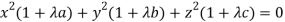
(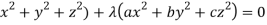
Hence we get-
f + 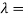 0 then
0 then 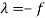
Put in (3) , (4) and (5), we get-
in (3) , (4) and (5), we get-
x(1 – fa) = 0 , y(1 – fb) = 0 and z(1 – fc) = 0
We get-
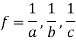
These gives the maximum and minimum values of f.
Question-11: Divide 24 into three parts such that the continued product of the first, square of second and cube of third may be maximum.
Let first number be x, second be y and third be z.
According to the question
Let the given function be f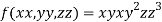
And the relation 
By Lagrange’s Method
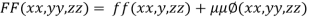
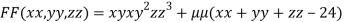 ….(i)
….(i)
Partially differentiating (i) with respect to x,y and z and equate them to zero
 ….(ii)
….(ii)
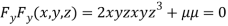 ….(iii)
….(iii)
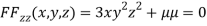 ….(iv)
….(iv)
From (ii),(iii) and (iv) we get

On solving
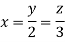
Putting it in given relation we get
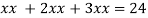
Or 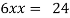
Or 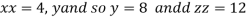
Thus the first number is 4 second is 8 and third is 12