Unit-5

Kinematics of particles

Question 1) The velocity of any point in mechanism relative to any other point on the mechanism on velocity polygon is represented by the line?

Answer 1) A link is rotating about O. Velocity of point P on link w.r.t. Point Q on link will be perpendicular to PQ.

The velocity of any point in mechanism relative to any other point on the mechanism on velocity polygon is represented by the line joining the corresponding points.

Q 2) Explain Grashof’s law?

Answer 2) Here P, Q, R, & S are the lengths of the links.

In a four-bar linkage, S denotes the shortest link length, L is the longest link length, P and Q are the lengths of other two links. At least one of the three moving links will rotate by 3600

According to Grashof’s law : “For a four bar mechanism, the sum of the shortest and longest link lengths should not be greater than the sum of remaining two link lengths, if there is to be continuous relative motion between the two links

S + L < P +Q

Question 3) Explain Kutzbach criterion

Answer 3) From the Kutzbach criterion the degree of freedom

n = 3(l − 1) − 2j − h

The minimum number of links in a single degree-of-freedom planar mechanism with both higher and lower kinematic pairs is

For single degree of Freedom (n = 1),
1 = 3(l − 1) − 2j − h
3l − 2j − 4 − h = 0 …(i)
The simplest possible mechanisms of single degree of freedom is four-bar mechanism. For this mechanism j = 4, h = 0
From equation (i), we have

3l − 2 x 4 − 4 − 0 = 0
or, l = 4

Question 5) A man walks 500 m due east in 300 s followed by 400 m due west in 320 s. Determine:

A) his average velocity for i) 500 m, ii) 400 m
B) his average velocity for the whole journey

Consider the direction east to be positive and the direction west to be negative. Therefore there will be no need to write the directions for distance and velocity as these will be shown as positive or negative numbers.

A) i) for 500 m: v = 500/300
v = 1.67 m/s

Ii) For 400m: v = -400/320
v = -1.25 m/s

B) The actual distance travelled in a particular direction in 620 seconds (300+320) is 500 + (-400) = 100 m in an easterly direction.

Although the man has walked a total distance of 900 m, he has effectively only walked 100 m east because he changed direction in the lat 400 m.

Therefore the actual distance travelled in a particular direction is called a displacement.
And the average velocity of the man = 100/(300 + 320)
                                                     = 0.16 m/s

Note that the average speed of the man will be:
900/620 = 1.45 m/s as the man has still walked 900 m in 620 s.

Q 6) A piece of wood of mass 0.03 kg is dropped from the top of a 100 m height building. At the same time, a bullet of mass 0.02 Kg is fired vertically upward, with a velocity 100 m/s, from the ground. The bullet gets embedded in the wood. Then the maximum height to which the combined system reaches above the top of the building before falling below is (g = 10 m/s)

A 6)

Suppose both collide at the point P after time t. Time taken for the particles to collide,

t = d/vrel = 100/100 = 1s

Speed of wood just before collision =gt = 10m/s

Speed of bullet just before collision

v -gt = 100 -10 = 90 m/s

Before

0.03 kg ↓ 10 m/s

0.02 kg ↑ 90 m/s

After

↑ v

0.05 kg

Now, the conservation of linear momentum just before and after the collision

-(0.03)(10) + (0.02)(90) = (0.05)v ⇒ v = 30 m/s

The maximum height reached by the body a = v2/2g

= (30)2/2(10)

= 45 m

(100 -h) = ½ gt2 = ½ x 10 x1 ⇒h = 95 m

Height above tower = 40 m

Answer: (d) 40 m

Q7: A passenger train of length 60 m travels at a speed of 80 km/hr. Another freight train of length 120 m travels at a speed of 30 km/hr. The ratio of times taken by the passenger train to completely cross the freight train when: (i) they are moving in the same direction, and (ii) in the opposite direction, is

A 7) The total distance to be travelled by train is 60 + 120 = 180 m.

When the trains are moving in the same direction, the relative velocity is v1 – v2 = 80 – 30 = 50 km hr–1.

So time taken to cross each other, t1 = 180/ (50 x 103/3600) = [(18 x 18)/25] s

When the trains are moving in opposite direction, relative velocity is |v1 – (–v2)| = 80 + 30 = 110 km hr–1

So time taken to cross each other

t2= 180/ (110 x 103/3600) = [(18 x 36)/110] s

t1 / t2= [(18 x 18)/25] / [(18 x 36)/110] = 11/5

Q8: A particle has an initial velocity 3 and an acceleration of 0.4i^+0.3j^​. Its speed after 10s is

Solution:

v = u + at

u = 3i + 4j + (0.4 i + 0.3 j) x 10

= 3i + 4j + 4i + 3i

u = 7i + 7j

u∣=√72+72​

Answer:72​ units

Q9: An automobile, travelling at 40 km/h, can be stopped at a distance of 40 m by applying brakes. If the same automobile is travelling at 80 km/h, the minimum stopping distance, in metres, is (assume no skidding):

A 9)

Using v2 = u2 – 2as

0 = u2 – 2as

S = u2 /2a

S1/S2 = u12/u22

S2 = (u12/u22)S1 = (2)2(40) = 160 m

Answer: (c)160 m

Q10: A body is thrown vertically upwards. Which one of the following graphs correctly represents the velocity vs time?

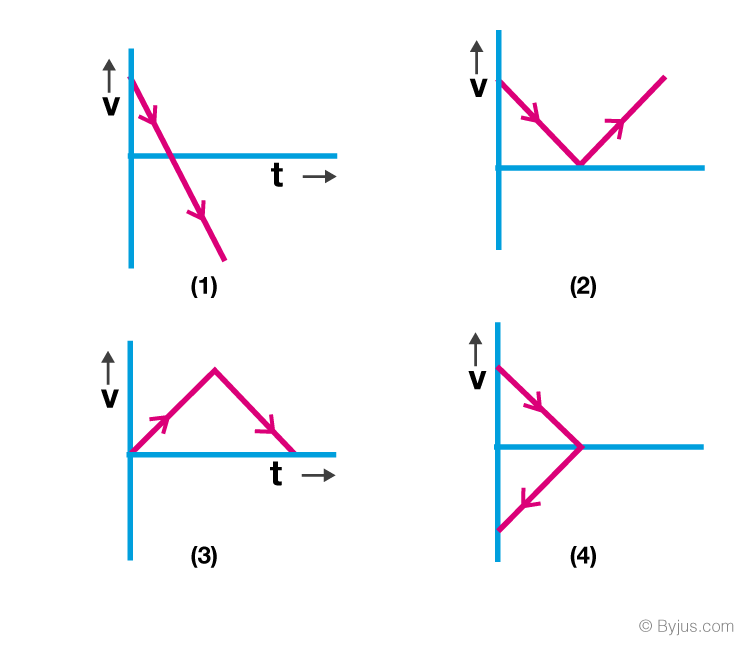
Solution:

Velocity at any time t is given by

v = u + at

v = v(0) + (-gt)

v = -gt

Answer:

Straight line with negative slope

Q11. A parachutist after bailing out falls 50 m without friction. When the parachute opens, it decelerates at 2 m/s2. He reaches the ground with a speed of 3 m/s. At what height, did he bailout?

A 11:

Initially, the parachutist falls under gravity u 2 = 2ah = 2 × 9.8 × 50 = 980 m2s –2

He reaches the ground with speed = 3 m/s,

a = –2 m s–2 ⇒ (3)2 = u 2 – 2 × 2 × h1

9 = 980 – 4 h1

h1 = 971/4

h1 = 242.75 m

Total height = 50 + 242.75 = 292.75 = 293 m.

Unit-5

Kinematics of particles

Question 1) The velocity of any point in mechanism relative to any other point on the mechanism on velocity polygon is represented by the line?

Answer 1) A link is rotating about O. Velocity of point P on link w.r.t. Point Q on link will be perpendicular to PQ.

The velocity of any point in mechanism relative to any other point on the mechanism on velocity polygon is represented by the line joining the corresponding points.

Q 2) Explain Grashof’s law?

Answer 2) Here P, Q, R, & S are the lengths of the links.

In a four-bar linkage, S denotes the shortest link length, L is the longest link length, P and Q are the lengths of other two links. At least one of the three moving links will rotate by 3600

According to Grashof’s law : “For a four bar mechanism, the sum of the shortest and longest link lengths should not be greater than the sum of remaining two link lengths, if there is to be continuous relative motion between the two links

S + L < P +Q

Question 3) Explain Kutzbach criterion

Answer 3) From the Kutzbach criterion the degree of freedom

n = 3(l − 1) − 2j − h

The minimum number of links in a single degree-of-freedom planar mechanism with both higher and lower kinematic pairs is

For single degree of Freedom (n = 1),
1 = 3(l − 1) − 2j − h
3l − 2j − 4 − h = 0 …(i)
The simplest possible mechanisms of single degree of freedom is four-bar mechanism. For this mechanism j = 4, h = 0
From equation (i), we have

3l − 2 x 4 − 4 − 0 = 0
or, l = 4

Question 5) A man walks 500 m due east in 300 s followed by 400 m due west in 320 s. Determine:

A) his average velocity for i) 500 m, ii) 400 m
B) his average velocity for the whole journey

Consider the direction east to be positive and the direction west to be negative. Therefore there will be no need to write the directions for distance and velocity as these will be shown as positive or negative numbers.

A) i) for 500 m: v = 500/300
v = 1.67 m/s

Ii) For 400m: v = -400/320
v = -1.25 m/s

B) The actual distance travelled in a particular direction in 620 seconds (300+320) is 500 + (-400) = 100 m in an easterly direction.

Although the man has walked a total distance of 900 m, he has effectively only walked 100 m east because he changed direction in the lat 400 m.

Therefore the actual distance travelled in a particular direction is called a displacement.
And the average velocity of the man = 100/(300 + 320)
                                                     = 0.16 m/s

Note that the average speed of the man will be:
900/620 = 1.45 m/s as the man has still walked 900 m in 620 s.

Q 6) A piece of wood of mass 0.03 kg is dropped from the top of a 100 m height building. At the same time, a bullet of mass 0.02 Kg is fired vertically upward, with a velocity 100 m/s, from the ground. The bullet gets embedded in the wood. Then the maximum height to which the combined system reaches above the top of the building before falling below is (g = 10 m/s)

A 6)

Suppose both collide at the point P after time t. Time taken for the particles to collide,

t = d/vrel = 100/100 = 1s

Speed of wood just before collision =gt = 10m/s

Speed of bullet just before collision

v -gt = 100 -10 = 90 m/s

Before

0.03 kg ↓ 10 m/s

0.02 kg ↑ 90 m/s

After

↑ v

0.05 kg

Now, the conservation of linear momentum just before and after the collision

-(0.03)(10) + (0.02)(90) = (0.05)v ⇒ v = 30 m/s

The maximum height reached by the body a = v2/2g

= (30)2/2(10)

= 45 m

(100 -h) = ½ gt2 = ½ x 10 x1 ⇒h = 95 m

Height above tower = 40 m

Answer: (d) 40 m

Q7: A passenger train of length 60 m travels at a speed of 80 km/hr. Another freight train of length 120 m travels at a speed of 30 km/hr. The ratio of times taken by the passenger train to completely cross the freight train when: (i) they are moving in the same direction, and (ii) in the opposite direction, is

A 7) The total distance to be travelled by train is 60 + 120 = 180 m.

When the trains are moving in the same direction, the relative velocity is v1 – v2 = 80 – 30 = 50 km hr–1.

So time taken to cross each other, t1 = 180/ (50 x 103/3600) = [(18 x 18)/25] s

When the trains are moving in opposite direction, relative velocity is |v1 – (–v2)| = 80 + 30 = 110 km hr–1

So time taken to cross each other

t2= 180/ (110 x 103/3600) = [(18 x 36)/110] s

t1 / t2= [(18 x 18)/25] / [(18 x 36)/110] = 11/5

Q8: A particle has an initial velocity 3 and an acceleration of 0.4i^+0.3j^​. Its speed after 10s is

Solution:

v = u + at

u = 3i + 4j + (0.4 i + 0.3 j) x 10

= 3i + 4j + 4i + 3i

u = 7i + 7j

u∣=√72+72​

Answer:72​ units

Q9: An automobile, travelling at 40 km/h, can be stopped at a distance of 40 m by applying brakes. If the same automobile is travelling at 80 km/h, the minimum stopping distance, in metres, is (assume no skidding):

A 9)

Using v2 = u2 – 2as

0 = u2 – 2as

S = u2 /2a

S1/S2 = u12/u22

S2 = (u12/u22)S1 = (2)2(40) = 160 m

Answer: (c)160 m

Q10: A body is thrown vertically upwards. Which one of the following graphs correctly represents the velocity vs time?

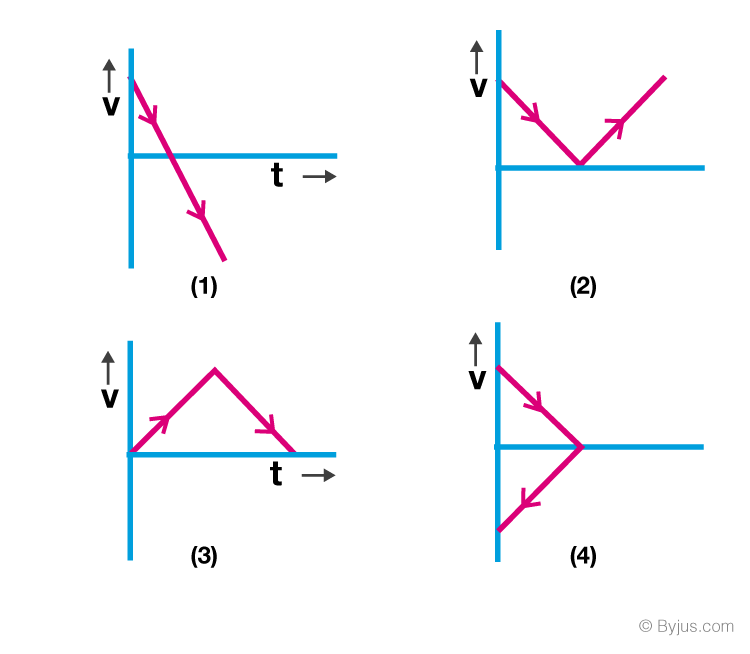
Solution:

Velocity at any time t is given by

v = u + at

v = v(0) + (-gt)

v = -gt

Answer:

Straight line with negative slope

Q11. A parachutist after bailing out falls 50 m without friction. When the parachute opens, it decelerates at 2 m/s2. He reaches the ground with a speed of 3 m/s. At what height, did he bailout?

A 11:

Initially, the parachutist falls under gravity u 2 = 2ah = 2 × 9.8 × 50 = 980 m2s –2

He reaches the ground with speed = 3 m/s,

a = –2 m s–2 ⇒ (3)2 = u 2 – 2 × 2 × h1

9 = 980 – 4 h1

h1 = 971/4

h1 = 242.75 m

Total height = 50 + 242.75 = 292.75 = 293 m.