Unit-6
Kinetics of Particles
Q 1: What is the angular velocity of a particle in a circular orbit, rotating at the rate of 200 times per minute?
A 1: In the given problem, the frequency of rotation is 200 times per minute
ω= 2πf
= 2π x 200/60 = 20.93 rad/s
Q 2: An electrically powered wheel is rotating about its axis at the rate of 900 rotations per minute. When the power is turned off it comes it rest in 1 minute. Find the angular deceleration of the wheel in rad/s2.
A 2: From the laws of motion in the case of rotational motion, we know that
ω = ω0 + αt.
From the given data:
ω0 = 900rpm = 900 x 2π/60 rad/s
ω = 0 and t= 60s
Hence angular deceleration α = π/2
Q 3: A bus is moving in a circular track of radius 1000cm with a speed of 10m/s. A pendulum is suspended from the roof of the bus by a light rigid rod of length 100cm. Find the angle made by the rod with the track. (Use g=10m/s2)
A 3:
Tan θ = v2/rg = 102/10×10
Tan θ = 1
Tan θ = 45⁰
Q 4: The minimum velocity with which a car driver must traverse a curve of radius 150m and coefficient of friction 0.6 to avoid skidding is?
A 4: In the relation mv2/r =µN substitute N = mg
We get v2 =µrg
v2 = 0.6x150x10
v= 30m/s
Q 5) Explain Speed and Velocity
A 5)
These terms are used to describe the rate of change of position. Speed is the rate of change of distance while velocity is the rate of change of displacement. Comparing from above as distance can never be negative so the speed is never negative while velocity can be both positive and negative. In mathematical terms, these are defined as follows:
Speed = Distance Travelled Time Taken
Velocity = (Final position–Initial position) Time Taken
Q 6) Describe Examples for Rectilinear Motion?
A 6)
Following are the rectilinear motion examples:
- The use of elevators in public places is an example of rectilinear motion.
- Gravitational forces acting on objects resulting in free fall is an example of rectilinear motion.
- Kids sliding down from a slide are a rectilinear motion.
- The motion of planes in the sky is a rectilinear motion.
Q 7) Explain Angular Velocity?
A 7)
It is defined as the rate of change in angular displacement of a particle in a circular motion. It is denoted by
ω = lim∆t→0 (∆θ/∆t) = dθ/dt
Angular velocity is measured in rad/s. Apart from angular velocity and angular speed, a particle in circular motion also possesses linear velocity and corresponding linear speed.
v= ds/dt
v= |ds/dt|; s is the displacement of the particle
Q 8) Write Relation between Linear Speed (V) and Angular Speed (Ω)
A8)
In vector form
v= ω x r
Where r is the position vector of the particle measured with respect to the centre of the circle
(Or)
v = rω
The acceleration of a particle in circular motion has two components:
- Tangential acceleration at: This is the component of acceleration in the direction of the velocity of the particle.
at= d|v|/dt
- Radial acceleration ar: This is the component of acceleration directed towards the centre of the circle. This component causes a change in the direction of the velocity of a particle in a circular motion.
ar= v2/r = rω2
Q 9) Explain Angular Acceleration?
A 9)
It is defined as the rate of change of angular velocity of the rotating particle. It is measured in rad/s2
α = dω /dt = d2θ/dt2
Circular motion can be uniform and non-uniform depending on the nature of acceleration of the particle. The motion is called uniform circular motion when the particle is moving along a circular path possessing a constant speed.
During circular motion, the velocity vector changes its direction at each point on the circle. This implies that the radial component of acceleration is always non-zero. The tangential component can take a positive or negative value in the case of non-uniform circular motion and a zero value in the case of uniform circular motion.
We understand that the acceleration of a particle in a circular motion is always directed towards the centre and is given by v2/r. Applying Newton’s second law of motion in this situation;
Fcen = mv2/r
Where m is the mass of the particle
Fc is the centripetal force directed towards the centre of the circular path as illustrated in
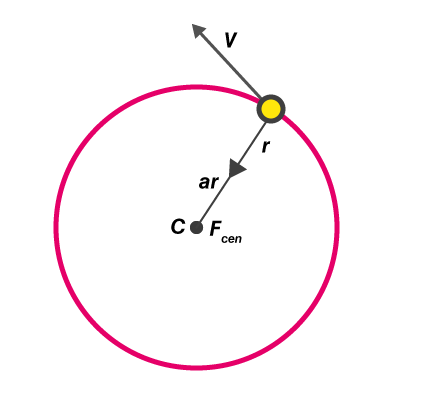
Fig 7
Examples of centripetal forces include gravitational force, the tension in a string and friction.
Q 10) Explain Moment Of Inertia of Sphere?
A 10)
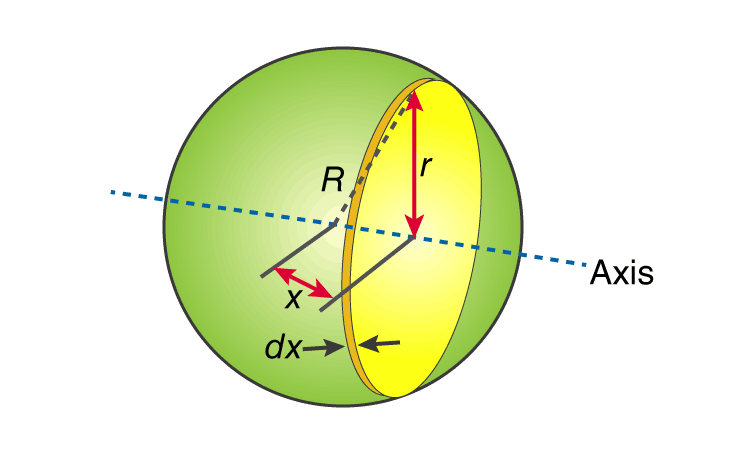
First, we take the moment of inertia of a disc that is thin. It is given as;
I = ½ MR2
In this case, we write it as;
DI (infinitesimally moment of inertia element) = ½ r2dm
Find the dm and dv using;
Dm = p dV
p = moment of a thin disk of mass dm
Dv = expressing mass dm in terms of density and volume
DV = π r2 dx
Now we replace dV into dm. We get;
Dm = p π r2 dx
And finally, we replace dm with dI
DI = ½ p π r4 dx
The next step involves adding x to the equation. If we look at the diagram we see that r, R and x forms a triangle. Now we will use Pythagoras theorem which gives us;
r2 = R2 – x2
Now if we substitute the values we get;
DI = ½ p π (R2 – x2)2 dx
This leads to:
I = ½ p π -R∫R (R2 – x2)2 dx
After integration and expanding we get;
I = pπ 8/15 R5
Additionally, we have to find the density as well. For that we use;
P (density) = M (mass) / V (volume)
p = M (mass) / (4/3 πR3)
If we substitute all the values;
I = 8/15 π [M / (4/3 πR3)] R5
I = ⅖ MR2
Unit-6
Kinetics of Particles
Q 1: What is the angular velocity of a particle in a circular orbit, rotating at the rate of 200 times per minute?
A 1: In the given problem, the frequency of rotation is 200 times per minute
ω= 2πf
= 2π x 200/60 = 20.93 rad/s
Q 2: An electrically powered wheel is rotating about its axis at the rate of 900 rotations per minute. When the power is turned off it comes it rest in 1 minute. Find the angular deceleration of the wheel in rad/s2.
A 2: From the laws of motion in the case of rotational motion, we know that
ω = ω0 + αt.
From the given data:
ω0 = 900rpm = 900 x 2π/60 rad/s
ω = 0 and t= 60s
Hence angular deceleration α = π/2
Q 3: A bus is moving in a circular track of radius 1000cm with a speed of 10m/s. A pendulum is suspended from the roof of the bus by a light rigid rod of length 100cm. Find the angle made by the rod with the track. (Use g=10m/s2)
A 3:
Tan θ = v2/rg = 102/10×10
Tan θ = 1
Tan θ = 45⁰
Q 4: The minimum velocity with which a car driver must traverse a curve of radius 150m and coefficient of friction 0.6 to avoid skidding is?
A 4: In the relation mv2/r =µN substitute N = mg
We get v2 =µrg
v2 = 0.6x150x10
v= 30m/s
Q 5) Explain Speed and Velocity
A 5)
These terms are used to describe the rate of change of position. Speed is the rate of change of distance while velocity is the rate of change of displacement. Comparing from above as distance can never be negative so the speed is never negative while velocity can be both positive and negative. In mathematical terms, these are defined as follows:
Speed = Distance Travelled Time Taken
Velocity = (Final position–Initial position) Time Taken
Q 6) Describe Examples for Rectilinear Motion?
A 6)
Following are the rectilinear motion examples:
- The use of elevators in public places is an example of rectilinear motion.
- Gravitational forces acting on objects resulting in free fall is an example of rectilinear motion.
- Kids sliding down from a slide are a rectilinear motion.
- The motion of planes in the sky is a rectilinear motion.
Q 7) Explain Angular Velocity?
A 7)
It is defined as the rate of change in angular displacement of a particle in a circular motion. It is denoted by
ω = lim∆t→0 (∆θ/∆t) = dθ/dt
Angular velocity is measured in rad/s. Apart from angular velocity and angular speed, a particle in circular motion also possesses linear velocity and corresponding linear speed.
v= ds/dt
v= |ds/dt|; s is the displacement of the particle
Q 8) Write Relation between Linear Speed (V) and Angular Speed (Ω)
A8)
In vector form
v= ω x r
Where r is the position vector of the particle measured with respect to the centre of the circle
(Or)
v = rω
The acceleration of a particle in circular motion has two components:
- Tangential acceleration at: This is the component of acceleration in the direction of the velocity of the particle.
at= d|v|/dt
- Radial acceleration ar: This is the component of acceleration directed towards the centre of the circle. This component causes a change in the direction of the velocity of a particle in a circular motion.
ar= v2/r = rω2
Q 9) Explain Angular Acceleration?
A 9)
It is defined as the rate of change of angular velocity of the rotating particle. It is measured in rad/s2
α = dω /dt = d2θ/dt2
Circular motion can be uniform and non-uniform depending on the nature of acceleration of the particle. The motion is called uniform circular motion when the particle is moving along a circular path possessing a constant speed.
During circular motion, the velocity vector changes its direction at each point on the circle. This implies that the radial component of acceleration is always non-zero. The tangential component can take a positive or negative value in the case of non-uniform circular motion and a zero value in the case of uniform circular motion.
We understand that the acceleration of a particle in a circular motion is always directed towards the centre and is given by v2/r. Applying Newton’s second law of motion in this situation;
Fcen = mv2/r
Where m is the mass of the particle
Fc is the centripetal force directed towards the centre of the circular path as illustrated in
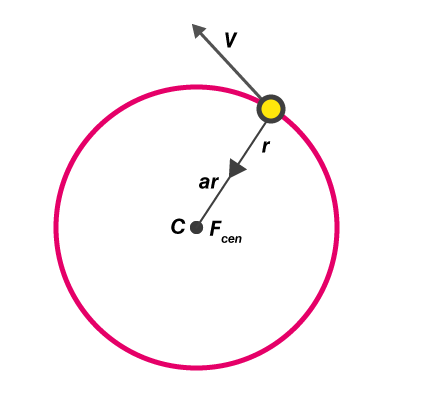
Fig 7
Examples of centripetal forces include gravitational force, the tension in a string and friction.
Q 10) Explain Moment Of Inertia of Sphere?
A 10)
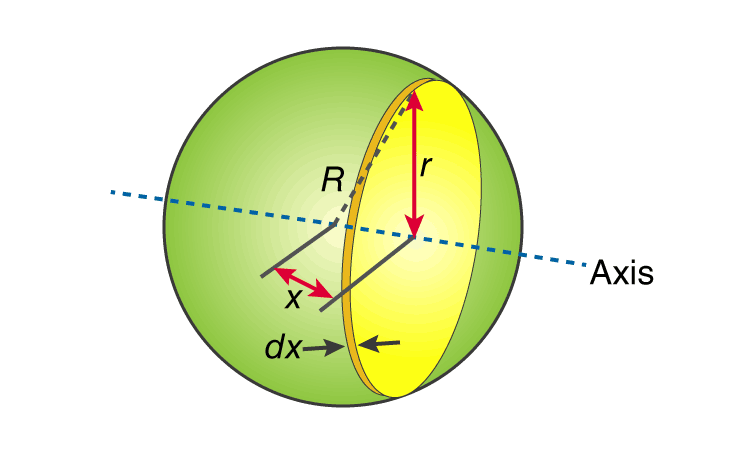
First, we take the moment of inertia of a disc that is thin. It is given as;
I = ½ MR2
In this case, we write it as;
DI (infinitesimally moment of inertia element) = ½ r2dm
Find the dm and dv using;
Dm = p dV
p = moment of a thin disk of mass dm
Dv = expressing mass dm in terms of density and volume
DV = π r2 dx
Now we replace dV into dm. We get;
Dm = p π r2 dx
And finally, we replace dm with dI
DI = ½ p π r4 dx
The next step involves adding x to the equation. If we look at the diagram we see that r, R and x forms a triangle. Now we will use Pythagoras theorem which gives us;
r2 = R2 – x2
Now if we substitute the values we get;
DI = ½ p π (R2 – x2)2 dx
This leads to:
I = ½ p π -R∫R (R2 – x2)2 dx
After integration and expanding we get;
I = pπ 8/15 R5
Additionally, we have to find the density as well. For that we use;
P (density) = M (mass) / V (volume)
p = M (mass) / (4/3 πR3)
If we substitute all the values;
I = 8/15 π [M / (4/3 πR3)] R5
I = ⅖ MR2