UNIT -2
CRYSTALLOGRAPHY
Q 1) Define the term Space Lattice?
A1)
In a solid crystalline material, the atoms or molecules are arranged regularly and periodically in all three dimensions. The atomic arrangement in a crystal is called crystal structure.
To explain crystal symmetries easily, it is convenient to represent an atom or a group of atoms that repeats in three dimensions in the crystal as a unit. If each such atom or unit of atoms in a crystal is replaced by a point in space, then the resultant points in space are called space lattice.
Each point in a space lattice is called a lattice point. Each atom or unit of atoms is called basis or pattern.
A space lattice represents the geometrical pattern of crystal in which the surroundings of each lattice point is the same. If the surroundings of each lattice point is same or if the atom or all the atoms at lattice points are identical, then such a lattice is called Bravais lattice.
On the other hand, if the atom or the atoms at lattice points are not same, then it is said to be a non-Bravais lattice.
A space lattice or crystal lattice is defined as three dimensional infinite arrays of points in space in which every point has surroundings identical to that of every other point in the array.
Q 2) Define Basis in Crystal Structure?
A 2)
The atomic arrangement in a crystal is called crystal structure. The crystal structure is formed by associating every lattice point with an atom or an assembly of atoms or molecules or ions, which are identical in composition, arrangement and orientation, called the basis. i.e. an atom, or a group of atoms or molecules identical in composition is called the basis or the pattern.
The basis provides the number of atoms per lattice point, their types, mutual orientations and distances of separation between the atoms.
If the basis is substituted for the lattice points, then the resulting structure is called crystal structure as shown in Figure.
Lattice + basis = crystal structure.
The basis shown in Figure contains two different atoms. In copper and sodium crystals the basis is single atoms; In NaCl, the basis is diatomic and in CaF2 the basis is triatomic. A lattice is an imaginary assumption while the crystal structure is a real concept.
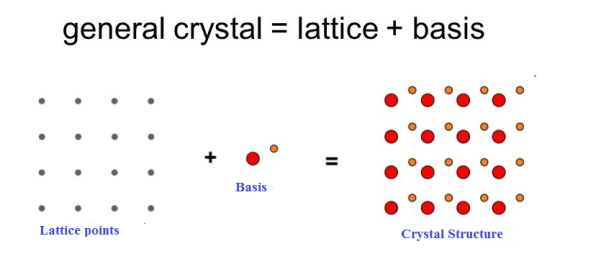
1 Figure: Lattice sites, Basis and crystal structure
Q 3) What is Unit Cell and also discuss about Lattice Parameters?
A3)
Unit cell
Unit cell is small repeating entity of the atomic structure. It is the basic building block of the crystal structure. It defines the entire crystal structure with the atom positions within.
Unit cells for most of the crystals are parallelepipeds or cubes having three sets of parallel faces. A unit cell is the basic structural unit or building block of the crystal.
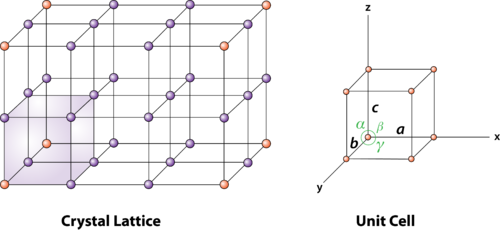
2 Figure: unit cell and unit cell parameter
A unit cell is defined as the smallest parallelepiped volume in the crystal, which on repetition along the crystallographic axes gives the actual crystal structure or the smallest geometric figure, which on repetition in three-dimensional space, gives the actual crystal structure is called a unit cell.
Choice of a unit cell is not unique but it can be constructed in a number of ways as shown in figure. Following figure shows different ways of representing unit cells in a two-dimensional lattice. A unit cell can be represented as ABCD or A′B′C′D′ or A′′B′′C′′D′′, etc.
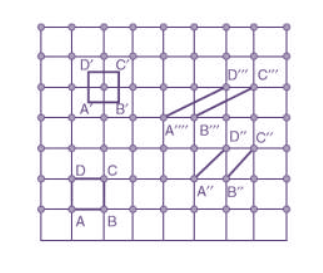
3 Figure: Construction of unit cell in different way
First we define crystallographic axes. These axes are obtained by the intersection of the three non-coplanar faces of the unit cell. The angles between these faces or crystallographic axes are known as interfacial or interaxial angles. The angles between the axes Y and Z is α, between Z and X is β and between X and Y is γ. The translational vectors or primitives a, b, c of a unit cell along X, Y, Z axes and interaxial angles α, β, γ are called Cell parameters. These cell parameters are shown in (Figure 2). The cell parameters determine the actual size and shape of the unit cell.
Q 4) What do you meant by Primitive and non-primitive unit cells?
A 4)
The unit cell formed by primitives is called a simple or a primitive unit cell. A primitive unit cell contains only one lattice point. If a unit cell contains more than one lattice point, then it is called a non-primitive unit cell or a multiple unit cell. Most of the unit cells of various crystal lattices contain two or more lattice points and hence it is not necessary that unit cell should be a primitive unit cell.
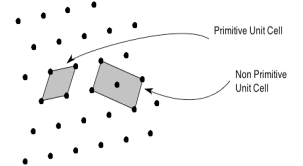
4 Figure: Primitive and non-primitive unit cells
Q 5) What are Bravais lattices?
A5)
If the surroundings of each lattice point is same or if the atom or all the atoms at lattice points are identical, then such a lattice is called Bravais lattice.
A space lattice represents the geometrical pattern of crystal in which the surroundings of each lattice point is the same. If the surroundings of each lattice point is same or if the atom or all the atoms at lattice points are identical, then such a lattice is called Bravais lattice.
On the other hand, if the atom or the atoms at lattice points are not same, then it is said to be a non-Bravais lattice.
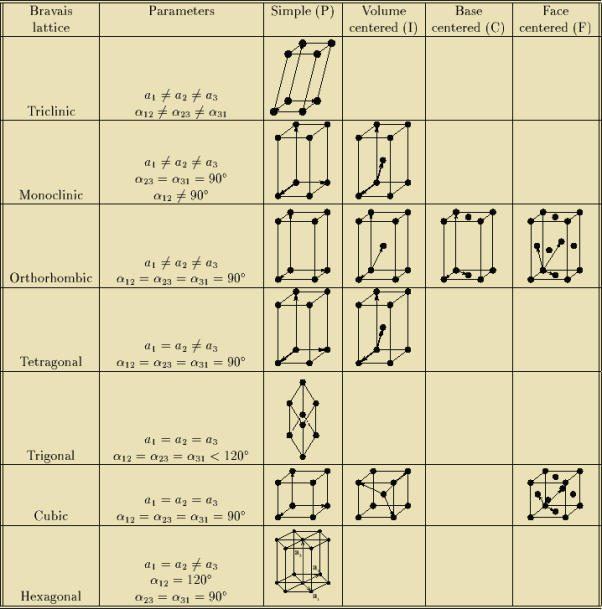
For representing the type of distribution of lattice points in space, seven different co-ordinate systems are required. These co-ordinate systems are called crystal systems.
The crystal systems are named on the basis of geometrical shape and symmetry. The seven crystal systems are:
(1) Cubic
(2) Tetragonal
(3) Orthorhombic
(4) Monoclinic
(5) Triclinic
(6) Trigonal (or Rhombohedral)
(7) Hexagonal.
In 1948, Bravais showed that 14 lattices are sufficient to describe all crystals. These 14 lattices are known as Bravais lattices and are classified into 7 crystal systems based on cell parameters or lattice points present per unit cell.
Q 6) Describe seven crystal systems with diagrams?
A 6)
Bravais lattices are categorized as
Q 7) Describe FCC crystal structure?
A 7)
Face-centered lattice (F)
Number of atoms
In case of face-centered lattice, in addition to the 8 atoms at 8 corners each contributing 1/8thto the unit cell, six atoms will be present at the center of six faces of the cell each contributing 1/2nd to the unit cell. Therefore number of atoms or lattice points in a face centered unit cell becomes 8 x 1/8 + 6 x 1/2 = 4.

Figure: Face-centered lattice (F)
Coordination number
In Face Centred Cubic system 12 neighbour atoms are in touch with the selected atom as shown in figure. So the coordination number of FCC is twelve.
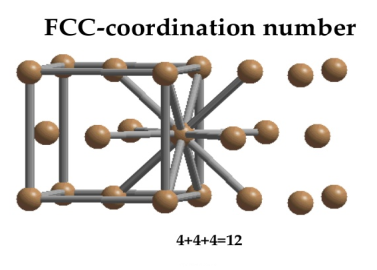
Figure: Face Centred Cubic Crystal
Atomic Radius
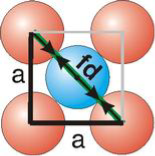
Fd | = | 4r |
|
|
|
|
|
|
Fd2 | = | a2 + a2 |
|
|
|
|
|
|
(4r)2 | = | 2a2 |
For FCC r = 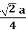
Q 8) Obtain the relations between the edge of the unit cell and atomic radius for the SC, BCC and FCC lattices?
A 8)
Atoms are not hard spheres with distinct boundaries, so their sizes are not determined directly. However, the positions of the atoms in a solid can be determined by x-ray diffraction, and the sizes of the atoms are inferred from those distances.
In this method, the radius of an atom is determined from the unit cell edge length (a), which is determined from the location of the atoms, and the assumption that the atoms touch as shown in below.
Simple or Primitive Cubic Crystal

2r = a
Body Centred Cubic Crystal
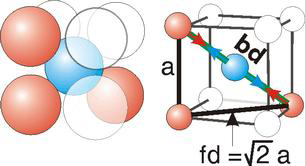
Bd | = | 4r |
|
|
|
|
|
|
Bd2 | = | Fd2 + a2 |
|
|
|
|
|
|
(4r)2 | = | 2a2 + a2 = 3a2 |
Face Centred Cubic Crystal
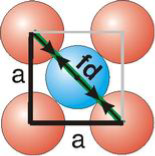
Fd | = | 4r |
|
|
|
|
|
|
Fd2 | = | a2 + a2 |
|
|
|
|
|
|
(4r)2 | = | 2a2 |
Relationship of Atomic Radii and Unit Cell Edge Lengths
Setting the edge length equal to 2r in the sc unit cell, and applying the Pythagorean theorem to the triangles shown in Figures we obtain the relationships between the atomic radius (r) of the atom and the edge length of the unit cell (a) given in Equation
For SC r = a/2
For BCC r = 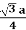
For FCC r = 
Q 9) Find the packing fraction for SC, BCC and FCC crystals?
A9)
Packing Efficiency
Packing efficiency is the fraction of the unit cell that is occupied by particles. Spheres cannot be packed without creating some void space, but the amount of void space depends upon how well they are packed. Packing efficiency (PE) is that fraction of the unit cell volume that is actually occupied by particles, not void space. Thus, the packing efficiency of a unit cell is
Packing Fraction = 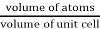 |
|
PE = 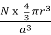 |
a = the length of a side of the unit cell, so a3 is the volume of the unit cell.
r = the radius of the atoms that occupy the unit cell, so (4/3)πr3 is the volume of a single atom in the unit cell.
N = the number of atoms in the unit cell, so N(4/3)πr3 is the volume occupied by all of the atoms in the unit cell.
The unit cell size (a) is directly proportional to the atom size (r), so one can be defined in terms of the other.
Consequently, the packing efficiency depends only upon the cell type, not its size. As shown in the next sections, the relationship between a and r depends only upon the unit cell type.
Packing in Simple Cubes
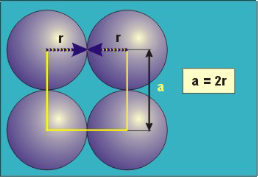
Figure
In the simple cubic unit cell, the spheres touch along the cell edge. Consequently, the edge length is two atomic radii
(a = 2r).
The properties of the simple cubic unit cell:
r = 0.5a
N = 1 atom/unit cell
PE = 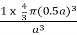 |
Packing efficiency = 52%
Coordination number = 6
Packing in Body-Centered Cubes
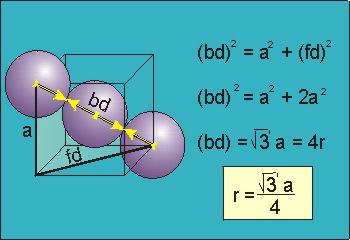
Figure
For the body-centered cubic unit cell, the spheres make contact along the body diagonal (bd), which is four atomic radii (each yellow arrow is one atomic radius), i.e., bd = 4r.
The body diagonal is related to the face diagonal (fd) and the cell edge (a) by the Pythagorean theorem. The relationship between the cell edge and the face diagonal was derived in the discussion of the fcc unit cell. The properties of the body-centered cubic unit cell:
For BCC r = 
r = 0.433 a
N = 2 atoms/unit cell
PE = 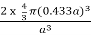 |
Packing efficiency = 68%
Coordination number = 8
Packing in Face-Centered Cubes
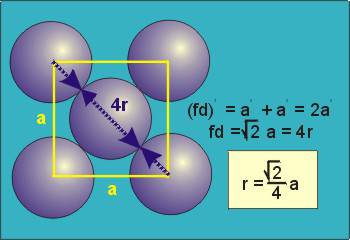
Figure
For FCC r = 
r= 0.354a
N = 4 atoms/unit cell
PE = 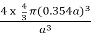 |
Packing efficiency = 74%
Coordination number = 12
As shown in the previous sections, the packing efficiency of a unit cell depends only on the cell type; it is independent of edge length and atomic radius because both cancel in the calculation. As might be expected, the packing efficiency increases as the number of atoms in the unit cell and the number of atoms that are packed around each atom (coordination number) increases.
Q 10) An atomic solid crystallizes in a body center cubic lattice and the inner surface of the atoms at the adjacent corner are separated by 60.3 pm. If the atomic weight of A is 48, Find the density of the solid?
A 10)
According to given condition,
0.13 a = 60.3 ⟹ a = 463.8
So Density = 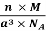
= 
= 1.75 g/cc
Q 11) Deduce the expression for the interplanar distance in terms of Miller indices for a cubic structure.
A 11)
Distance of separation between successive hkl planes
The separation between successive parallel planes in rectangular axes crystal system can be extracted easily.
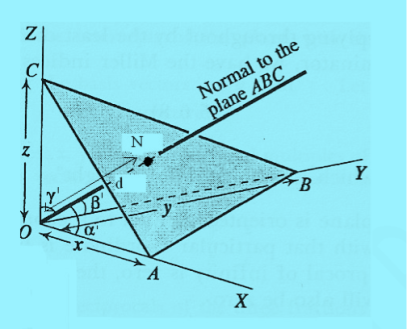
Consider a plane ABC which belongs to a family of planes. h, k, l are the Miller indices of this plane, which represents the set of planes. The perpendicular ON from the origin O to the plane represents the inter-planar spacing d = ON of this family of planes. Let ON make an angle α’, β’, γ’ with the x, y, z axes respectively.
The intercepts of the plane on the three axes are OA= a/h; OB= a/k; OC=a/l Where ‘a’ is the length of the cube edge. Then from figure, we have
Cos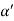 =
=  =
=  =
= 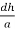
Cos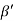 =
= 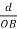 =
= 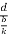 =
= 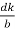
Cos =
=  =
=  =
= 
From the figure ON = 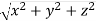
d = 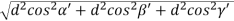
But, 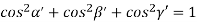
Substituting the values of cos’, cos’, cos’ in equation (2), We get,
For the orthogonal coordinates Substituting the values of cos’, cos’, cos’ in equation (2), We get,
( 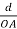 )2 + (
)2 + (  )2 +(
)2 +(  )2 = 1
)2 = 1
( )2 + (
)2 + (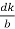 )2 +(
)2 +( )2 = 1
)2 = 1
( ) (
) (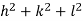 ) = 1
) = 1
d = 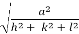
d = 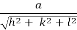
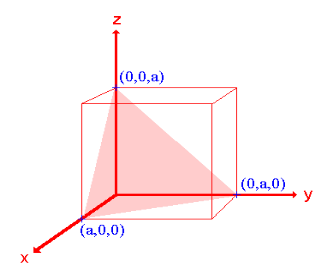
Q 12) Sketch the following planes of a cubic unit cell: (111) and (210)
A 12)
- The (111) surface
Intercepts: a , a , a
Fractional intercepts: 1 , 1 , 1
Miller Indices: (111)
 |
|
|
Ii. The (210) surface
Intercepts: ½a , a , 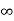
Fractional intercepts: ½ , 1 , 
Miller Indices: (210)
 |
|
Q 13) Explain Bragg’s Law and its importance?
A13)
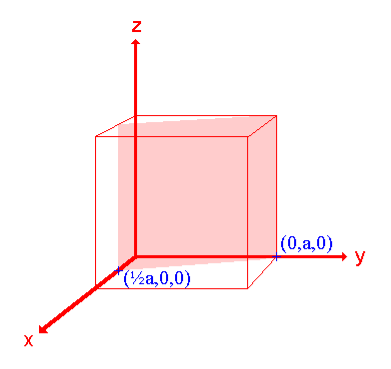
Consider a set of parallel planes called Bragg’s planes. Each atom is acting as a scattering center. The intensity of the reflected beam at certain angles will be maximum when the path difference between two reflected waves from two adjacent planes is an integral multiple of λ.
Let ‘d’ be the distance between two adjacent planes, 'λ’ be the wavelength of the incident x-ray, ‘θ’ be the glancing angle.
The path difference between the rays reflected at A & B is given by
 = CB + BD= d sinθ + d sinθ = 2dsinθ
= CB + BD= d sinθ + d sinθ = 2dsinθ
If the two consecutive planes scatter waves in phase with each other, then the path difference must be an integral multiple of wavelength.
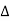 = nλ
= nλ
For the reflected light intensity to be maximum, the path difference
nλ= 2dsinθ
Where ‘n’ is the order of scattering.
This is called Bragg’s law
Therefore, Bragg’s law states that X-rays diffracted from different parallel planes of a crystal interfere constructively when the path difference is integral multiples of wavelength of X-rays.
From Bragg’s law nλ = 2d sin θ, since maximum possible value for sin θ is 1,
nλ/2d ≤ 1 or λ ≤ 2d.
This sets the limitation on the wavelength, i.e. in order to get the diffraction pattern by a crystal, the wavelength of X-rays should not exceed twice the inter-planar spacing.
Importance of Bragg’s law:
1. Bragg’s law is the essential condition to be satisfied by crystal planes in order to get diffraction pattern from a crystal.
2. It is used to calculate inter-planar spacing. Knowing the values of inter-planar spacing, lattice parameters can be determined.
Q 14) In a diffractometer, X-rays with a wavelength of 0.1315 nm were used to produce a diffraction pattern for copper. The first order diffraction (n = 1) occurred at an angle θ = 25.25°. Determine the spacing between the diffracting planes in copper.
A 14)
The distance between the planes is found by solving the Bragg equation,
nλ = 2d sin θ,
For d.
This gives: d=nλ2sinθ
=1(0.1315nm)2sin(25.25∘)=0.154nm