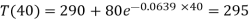Unit - 1
ODE of First order and Degree and Application
Q1) Define differential equations.
A1)
Differential Equations (Definition) –
A differential equation is an equation involving an unknown function and
Its derivatives.
Ex. 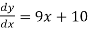
“A differential equation is an ordinary differential equationif the unknown function depends on only one independent variable.”
Notation:
The expression y’, y’’ , y’’’ …….yⁿ are used to represent derivatives.
Here, y’ = 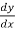 , y’’ =
, y’’ =  and so on.
and so on.
Q2) What do you understand by the degree and order of a differential equations?
A2)
Order:
The order is the highest derivative:
For example:
(1)  + y³ = 8x , here it has only first derivative so its ‘first order’.
+ y³ = 8x , here it has only first derivative so its ‘first order’.
(2) 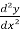 + y³ = 7x , here it has a second derivative so its ‘second order’ and so on.
+ y³ = 7x , here it has a second derivative so its ‘second order’ and so on.
Degree:
Degree is known as the exponent of higher derivative.
For example:
1.  )² + y³ = 8x, here its highest derivative has an exponent of 2, it is a first order second degree ordinary differential equation.
)² + y³ = 8x, here its highest derivative has an exponent of 2, it is a first order second degree ordinary differential equation.
2.  ) +
) +  y³ = 8x, here in this example its higher derivative has no exponent, so we can say that this is the third order and first degree ordinary differential equation.
y³ = 8x, here in this example its higher derivative has no exponent, so we can say that this is the third order and first degree ordinary differential equation.
Q3) From the differential equation by eliminating arbitrary constant.
y² = Ax² + Bx² + C
A3)
We will differentiate the given function, we get
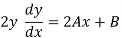
Again differentiate,
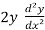 + 2
+ 2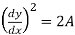
On differentiating again, we get
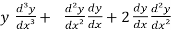 = 0
= 0
Q4) Obtain the differential equation of  here c is a constant and ‘a’ is a variable.
here c is a constant and ‘a’ is a variable.
A4)
Here we have,
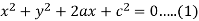
Differentiate with respect to ‘x’, we get-
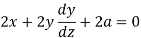
Or

Put this value in (1),
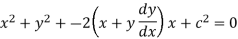
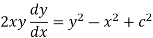
Which is the required DE.
Q5) Find the general solution of x 2 – 4x³
2 – 4x³
A5)
Rearranging the given equation:
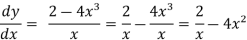
On integrating both sides,
y =  = 2 In x -
= 2 In x -  + c
+ c
This is the general solution.
Q6) Find the general solution of  = 3 + 2y
= 3 + 2y
A6)
Here, 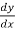 = 3 + 2y gives,
= 3 + 2y gives,
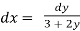 ,
,
Integrating both sides,
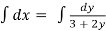 ,
,
By substitution, u = (3 +2y),
X =  In(3 + 2y) + c.
In(3 + 2y) + c.
Q7) Determine the particular solution of  = 2
= 2 , given that t = 0, when θ = 0
, given that t = 0, when θ = 0
A7)
 = 2
= 2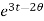 = 2
= 2 ,
,
 = 2
= 2 dt
dt
 dθ =
dθ =  dt
dt
Now integrating both sides,
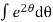 =
= 
The general solution is,
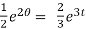 + c.
+ c.
When t = 0 and θ = 0, c =
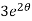 =
= 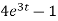
Q8) What is an exact differential equation?
A8)
An exact differential equation is formed by differentiating its solution directly without any other process,
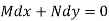
Is called an exact differential equation if it satisfies the following condition-
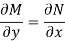
Here
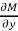 is the differential co-efficient of M with respect to y keeping x constant and
is the differential co-efficient of M with respect to y keeping x constant and 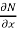 is the differential co-efficient of N with respect to x keeping y constant.
is the differential co-efficient of N with respect to x keeping y constant.
Q9) Solve 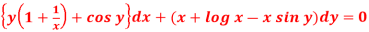
A9)
Here M =  and N =
and N = 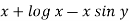

Then the equation is exact and its solution is-
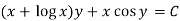
Q10) Determine whether the differential function ydx –xdy = 0 is exact or not.
A10)
Here the equation is the form of M(x , y)dx + N(x , y)dy = 0
But, we will check for exactness,
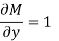
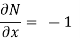
These are not equal results, so we can say that the given diff. Eq. Is not exact.
Q11) Solve-

A11)
Here, M =  and N =
and N = 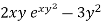
So that-
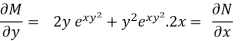
Thus the equation is exact and its solution is-
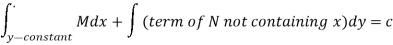
Which means-
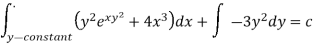
Or

Q12) Solve-
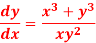
A12)
We can write the given equation as-
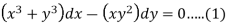
Here,
M = 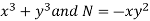
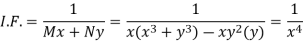
Multiply equation (1) by 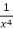 we get-
we get-
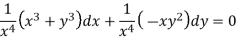
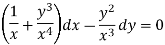
This is an exact differential equation-
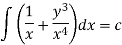
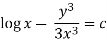
Q13) Solve-

A13)
Here given,
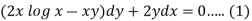
M = 2y and N = 2x log x - xy
Then-
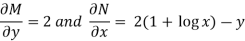
Here,

Then,

Now multiplying equation (1) by 1/x, we get-


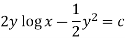
Q14) Solve-
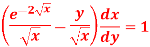
A14)
We can write the given equation as-
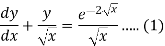
So that-
I.F. = 
The solution of equation (1) will be-
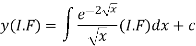
Or
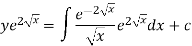
Or
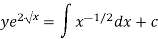
Or
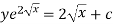
Q15) Solve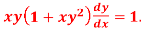
A15)
We can write the equation as-
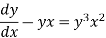
On dividing by 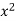 , we get-
, we get-
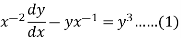
Put  so that
so that 
Equation (1) becomes,
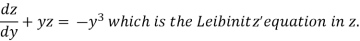
Here,
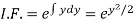
Therefore the solution is-
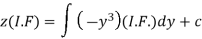
Or
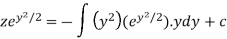
Now put 
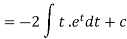
Integrate by parts-
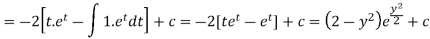
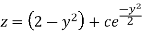
Or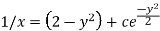
Q16) Solve- 
A16)
Here given-
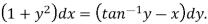
We can re-write this as-
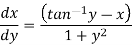
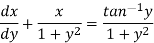
Which is a linear differential equation-
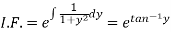
The solution will be-
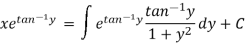
Put 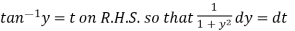
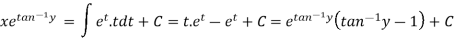

Q17) If the family of curves is xy = c, then find its orthogonal trajectory.
A17)
First we will differentiate the given equation with respect to x,
We get,
y + x 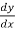 = 0
= 0
 =
= 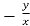
Replace  by
by 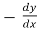
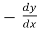 =
= 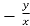
 =
= 
We get,
Ydy = x dx
Now integrate this equation, we get
 =
= 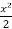 + c
+ c
y² - x² = 2c
Q18) Find the orthogonal trajectory of  .
.
A18)
Differentiate the equation with respect to r, we get-
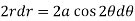
Now eliminate 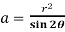 , we get-
, we get-
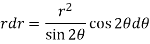
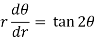
Differential equation of orthogonal trajectory-
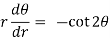
On solving-


On integrating-
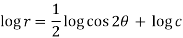
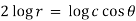
Orthogonal trajectory-
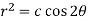
Q19) A capacitor c = 0.01 F in series with a resistor R = 20 ohms is charged from a battery E0 = 10 V. Assuming that initially the capacitor is completely uncharged, determine the charge Q(t), voltage v(t) on the capacitor and the current I (t) in the circuit.
A19)
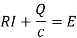
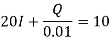

The general solution is-
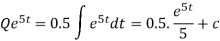
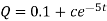
At t = 0, Q = 0
So that-
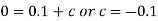
Thus, Q(t) = 0.1 (1 – 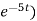
Voltage,
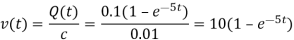
The current I(t) = dQ/dt = 
Q20) If a substance cools from 370 k to330 k in 10 mts, when the temperature of the surrounding air is 290 k, find the temperature of the substance after 40 mts.
A20)
Here we have,

So that the solution is-

Using condition T(0) = 370 to find c.
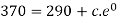
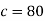
Thus-
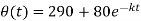
Now use condition,
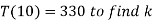
Thus
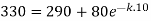
So that-
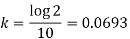
So that the required solution is-
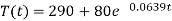
Putting t = 40mts in the equation-
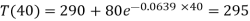
Unit - 1
ODE of First order and Degree and Application
Q1) Define differential equations.
A1)
Differential Equations (Definition) –
A differential equation is an equation involving an unknown function and
Its derivatives.
Ex. 
“A differential equation is an ordinary differential equationif the unknown function depends on only one independent variable.”
Notation:
The expression y’, y’’ , y’’’ …….yⁿ are used to represent derivatives.
Here, y’ = 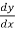 , y’’ =
, y’’ =  and so on.
and so on.
Q2) What do you understand by the degree and order of a differential equations?
A2)
Order:
The order is the highest derivative:
For example:
(1)  + y³ = 8x , here it has only first derivative so its ‘first order’.
+ y³ = 8x , here it has only first derivative so its ‘first order’.
(2)  + y³ = 7x , here it has a second derivative so its ‘second order’ and so on.
+ y³ = 7x , here it has a second derivative so its ‘second order’ and so on.
Degree:
Degree is known as the exponent of higher derivative.
For example:
1.  )² + y³ = 8x, here its highest derivative has an exponent of 2, it is a first order second degree ordinary differential equation.
)² + y³ = 8x, here its highest derivative has an exponent of 2, it is a first order second degree ordinary differential equation.
2.  ) +
) +  y³ = 8x, here in this example its higher derivative has no exponent, so we can say that this is the third order and first degree ordinary differential equation.
y³ = 8x, here in this example its higher derivative has no exponent, so we can say that this is the third order and first degree ordinary differential equation.
Q3) From the differential equation by eliminating arbitrary constant.
y² = Ax² + Bx² + C
A3)
We will differentiate the given function, we get
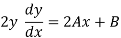
Again differentiate,
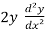 + 2
+ 2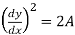
On differentiating again, we get
 = 0
= 0
Q4) Obtain the differential equation of  here c is a constant and ‘a’ is a variable.
here c is a constant and ‘a’ is a variable.
A4)
Here we have,

Differentiate with respect to ‘x’, we get-
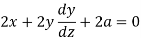
Or

Put this value in (1),
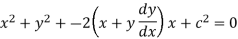
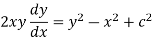
Which is the required DE.
Q5) Find the general solution of x 2 – 4x³
2 – 4x³
A5)
Rearranging the given equation:
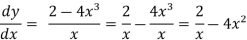
On integrating both sides,
y =  = 2 In x -
= 2 In x - 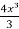 + c
+ c
This is the general solution.
Q6) Find the general solution of  = 3 + 2y
= 3 + 2y
A6)
Here,  = 3 + 2y gives,
= 3 + 2y gives,
 ,
,
Integrating both sides,
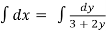 ,
,
By substitution, u = (3 +2y),
X =  In(3 + 2y) + c.
In(3 + 2y) + c.
Q7) Determine the particular solution of 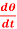 = 2
= 2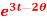 , given that t = 0, when θ = 0
, given that t = 0, when θ = 0
A7)
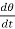 = 2
= 2 = 2
= 2 ,
,
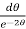 = 2
= 2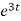 dt
dt
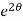 dθ =
dθ = 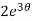 dt
dt
Now integrating both sides,
 =
= 
The general solution is,
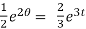 + c.
+ c.
When t = 0 and θ = 0, c =
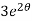 =
= 
Q8) What is an exact differential equation?
A8)
An exact differential equation is formed by differentiating its solution directly without any other process,

Is called an exact differential equation if it satisfies the following condition-
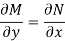
Here
 is the differential co-efficient of M with respect to y keeping x constant and
is the differential co-efficient of M with respect to y keeping x constant and 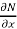 is the differential co-efficient of N with respect to x keeping y constant.
is the differential co-efficient of N with respect to x keeping y constant.
Q9) Solve 
A9)
Here M =  and N =
and N = 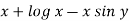
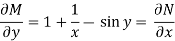
Then the equation is exact and its solution is-
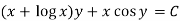
Q10) Determine whether the differential function ydx –xdy = 0 is exact or not.
A10)
Here the equation is the form of M(x , y)dx + N(x , y)dy = 0
But, we will check for exactness,
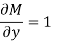
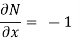
These are not equal results, so we can say that the given diff. Eq. Is not exact.
Q11) Solve-

A11)
Here, M =  and N =
and N = 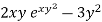
So that-
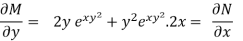
Thus the equation is exact and its solution is-
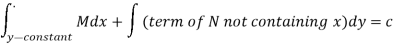
Which means-
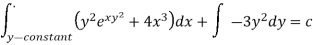
Or
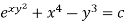
Q12) Solve-

A12)
We can write the given equation as-
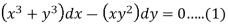
Here,
M = 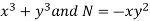
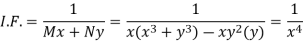
Multiply equation (1) by  we get-
we get-
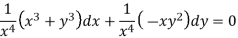

This is an exact differential equation-
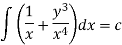
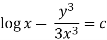
Q13) Solve-

A13)
Here given,
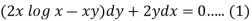
M = 2y and N = 2x log x - xy
Then-

Here,
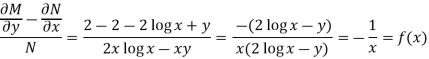
Then,
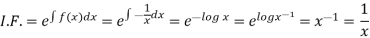
Now multiplying equation (1) by 1/x, we get-
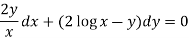
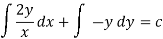
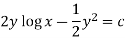
Q14) Solve-
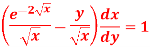
A14)
We can write the given equation as-
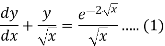
So that-
I.F. = 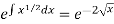
The solution of equation (1) will be-

Or
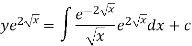
Or
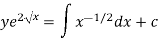
Or
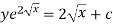
Q15) Solve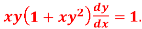
A15)
We can write the equation as-
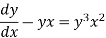
On dividing by 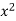 , we get-
, we get-
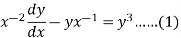
Put  so that
so that 
Equation (1) becomes,
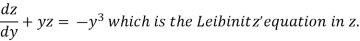
Here,
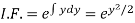
Therefore the solution is-
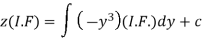
Or

Now put 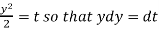
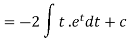
Integrate by parts-
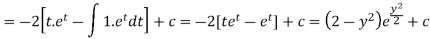
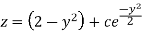
Or
Q16) Solve- 
A16)
Here given-

We can re-write this as-
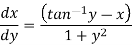
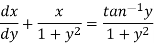
Which is a linear differential equation-
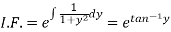
The solution will be-
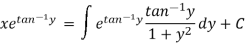
Put 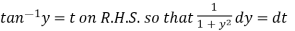
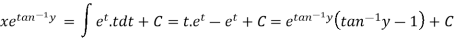

Q17) If the family of curves is xy = c, then find its orthogonal trajectory.
A17)
First we will differentiate the given equation with respect to x,
We get,
y + x 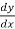 = 0
= 0
 =
= 
Replace  by
by 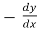
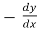 =
= 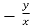
 =
= 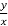
We get,
Ydy = x dx
Now integrate this equation, we get
 =
= 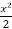 + c
+ c
y² - x² = 2c
Q18) Find the orthogonal trajectory of  .
.
A18)
Differentiate the equation with respect to r, we get-
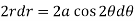
Now eliminate  , we get-
, we get-

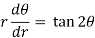
Differential equation of orthogonal trajectory-

On solving-
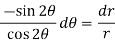
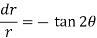
On integrating-
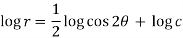
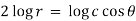
Orthogonal trajectory-
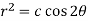
Q19) A capacitor c = 0.01 F in series with a resistor R = 20 ohms is charged from a battery E0 = 10 V. Assuming that initially the capacitor is completely uncharged, determine the charge Q(t), voltage v(t) on the capacitor and the current I (t) in the circuit.
A19)
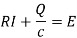
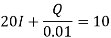
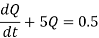
The general solution is-
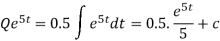
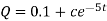
At t = 0, Q = 0
So that-
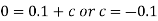
Thus, Q(t) = 0.1 (1 – 
Voltage,
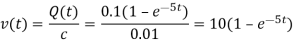
The current I(t) = dQ/dt = 
Q20) If a substance cools from 370 k to330 k in 10 mts, when the temperature of the surrounding air is 290 k, find the temperature of the substance after 40 mts.
A20)
Here we have,
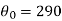
So that the solution is-
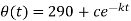
Using condition T(0) = 370 to find c.
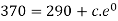
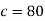
Thus-
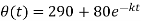
Now use condition,
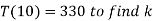
Thus

So that-

So that the required solution is-
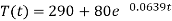
Putting t = 40mts in the equation-