Unit - 2
Infinite series
Q1) Define a sequence.
A1)
Sequence:
A function f: N 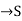 , where S is a non-empty set, is called sequence, for each nϵN.
, where S is a non-empty set, is called sequence, for each nϵN.
The sequence is written as f (1),f (2),f (3),f (4) ………. f(n).
Any sequence f(n) can be denoted as <f(n)> or {f(n)} or (f(n)).
Suppose f(n) = 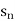
Then it can be written as - 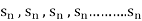 and can be denoted as <
and can be denoted as <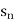 >or {
>or {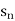 } or (
} or (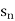 )
)
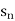 is the n’th term of the sequence.
is the n’th term of the sequence.
Q2) What is limit of a sequence?
A2)
Limit of a Sequence- A sequence < > is said to tend to limit “l”, when given any positive number ‘ϵ’, however small, we can always find an integer ‘m’ such that |
> is said to tend to limit “l”, when given any positive number ‘ϵ’, however small, we can always find an integer ‘m’ such that |  – l| <ϵ, for every for all, n≥m, and we can define this as follows,
– l| <ϵ, for every for all, n≥m, and we can define this as follows,
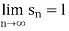
Q3) If 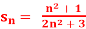 , then the limit of
, then the limit of  will be
will be
A3)
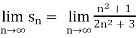 =
=  =
= 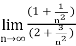 = ½
= ½
Hence the limit of the sequence is 1/2.
Q4) Define convergent and divergent sequences.
A4)
Convergent sequence- A sequence Sn is said to be convergent when it tends to a finite limit. That means the limit of a sequence Sn will be always finite in case of convergent sequence.
Divergent sequence- when a sequence tends to ±∞ then it is called divergent sequence.
Q5) Check whether the series 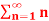 is convergent or divergent. Find its value in case of convergent.
is convergent or divergent. Find its value in case of convergent.
A5)
As we know that,
Sn = 
Therefore,
Sn = 
Now find out the limit of the sequence,
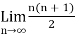 = ∞
= ∞
Here the value of the limit is infinity, so that the series is divergent as sequence diverges.
Q6) Check whether the series  is convergent or divergent.
is convergent or divergent.
A6)
The general formula can be written as,
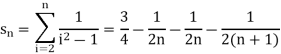
We get on applying limits,
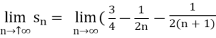 ) = 3/4
) = 3/4
This is the convergent series and its value is 3 / 4
Q7) Prove that the following series is convergent and find its sum.

A7)
Here,

And
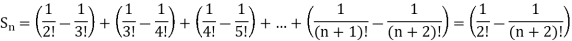
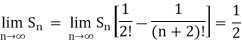
Hence the series is convergent and the limit is 1/2.
Q8) Test for absolute convergence:

A8)
Let the series is 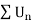 ,
,
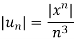

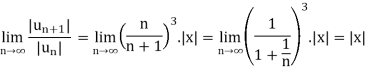
By ratio test,
 is convergent, if |x|<1.
is convergent, if |x|<1.
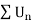 is absolutely convergent if |x|< 1.
is absolutely convergent if |x|< 1.
Q9) Show that the series 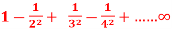 is absolutely convergent.
is absolutely convergent.
A9)
We have,

|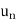 | =
| = 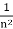 and |
and |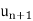 | =
| = 
The first condition and second conditions are-
1. | |<|
|<|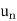 |
|
2. 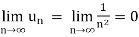
Both the conditions are satisfied.
So that we can say that by Leibnitz’s rule, the series is convergent.
The series is also convergent by p-test as p = 2 > 1.
Hence the given series is absolutely convergent.
Q10) Test the convergence/Divergence of the series:

A10)
Here the given series is alternately negative and positive, which is also a geometric infinite series.
1. Suppose,
S = 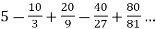
According to the conditions of geometric series,
Here, a = 5, and common ratio (r) = -2/3
Thus, we know that,

So,
Sum of the series is finite, which is 3.
So, we can say that the given series is convergent.
Now.
Again, sum of the positive terms,
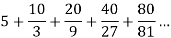
The series is geometric, then
A = 5 and r = 2/3, then
Sum of the series,
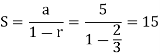
Sum of the series is finite then the series is convergent.
Both conditions are satisfied, then the given series is absolutely convergent.
Q11) Test the series for absolute/conditional convergence.
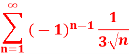
A11)
The given series is an alternating series of the form,

Here,
1.
2.
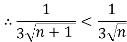

And,
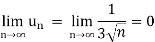
Hence bt Leibnitz’s test, the given series is convergent,
But,

Is divergent by p-series test.
So that, the given series is conditionally convergent.
Q12) Test the convergence of the series whose nth term is given below-

A12)
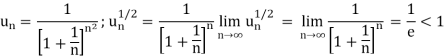
By root test 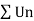 is convergent.
is convergent.
Q13) Test the convergence of the series whose nth term is given below-

A13)
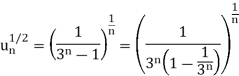
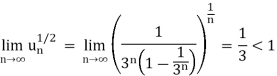
By root test 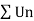 is convergent.
is convergent.
Q14) Test the convergence of the following series:

A14)
Here, we have,
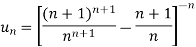
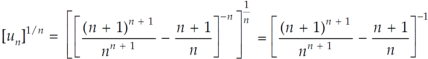
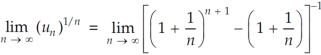
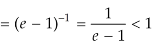
Therefore, the given series is convergent.
Q15) Test the convergence of the following series.
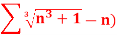
A15)
We have 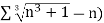
First, we will find  and the
and the 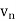



And
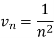

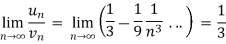
Here, we can see that, the limit is finite and not zero,
Therefore,  and
and 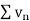 converges or diverges together.
converges or diverges together.
Since 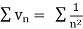 is of the form
is of the form  where p = 2>1
where p = 2>1
So that, we can say that,
 is convergent, so that
is convergent, so that 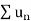 will also be convergent.
will also be convergent.
Q16) Show that the following series is convergent.

A16)
Here we have

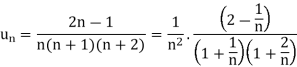
Suppose,



Which is finite and not zero.
By comparison test  and
and 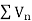 converge or diverge together.
converge or diverge together.
But,
Is convergent. So that 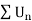 is also convergent.
is also convergent.
Q17) Test the convergence of the series whose n’th term is given below- n’th term = 
A17)
We have
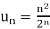 and
and 
By D’Alembert ratio test,

So that by D’Alembert ratio test, the series will be convergent.
Q18) Test for the convergence of the n’th term of the series given below-
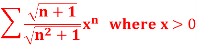
A18)
We have,
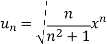

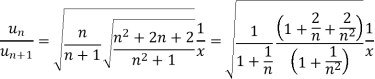
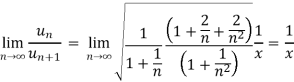
Now, by D’Alembert ratio test 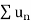 converges if
converges if 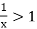 and diverges if
and diverges if 
At x = 1, this test fails.
Now, when x = 1

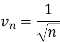
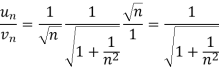
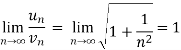
The limit is finite and not zero.
Then by comparison test,  converges or diverges together.
converges or diverges together.
Since 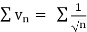 is the form of
is the form of 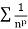 , in which
, in which 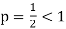
Hence  diverges then
diverges then 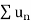 will also diverge.
will also diverge.
Therefore, in the given series  converges if x<1 and diverges if x≥1.
converges if x<1 and diverges if x≥1.
Unit - 2
Infinite series
Q1) Define a sequence.
A1)
Sequence:
A function f: N 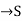 , where S is a non-empty set, is called sequence, for each nϵN.
, where S is a non-empty set, is called sequence, for each nϵN.
The sequence is written as f (1),f (2),f (3),f (4) ………. f(n).
Any sequence f(n) can be denoted as <f(n)> or {f(n)} or (f(n)).
Suppose f(n) = 
Then it can be written as - 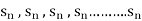 and can be denoted as <
and can be denoted as < >or {
>or { } or (
} or ( )
)
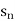 is the n’th term of the sequence.
is the n’th term of the sequence.
Q2) What is limit of a sequence?
A2)
Limit of a Sequence- A sequence < > is said to tend to limit “l”, when given any positive number ‘ϵ’, however small, we can always find an integer ‘m’ such that |
> is said to tend to limit “l”, when given any positive number ‘ϵ’, however small, we can always find an integer ‘m’ such that |  – l| <ϵ, for every for all, n≥m, and we can define this as follows,
– l| <ϵ, for every for all, n≥m, and we can define this as follows,

Q3) If 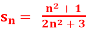 , then the limit of
, then the limit of  will be
will be
A3)
 =
=  =
=  = ½
= ½
Hence the limit of the sequence is 1/2.
Q4) Define convergent and divergent sequences.
A4)
Convergent sequence- A sequence Sn is said to be convergent when it tends to a finite limit. That means the limit of a sequence Sn will be always finite in case of convergent sequence.
Divergent sequence- when a sequence tends to ±∞ then it is called divergent sequence.
Q5) Check whether the series  is convergent or divergent. Find its value in case of convergent.
is convergent or divergent. Find its value in case of convergent.
A5)
As we know that,
Sn = 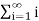
Therefore,
Sn = 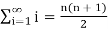
Now find out the limit of the sequence,
 = ∞
= ∞
Here the value of the limit is infinity, so that the series is divergent as sequence diverges.
Q6) Check whether the series  is convergent or divergent.
is convergent or divergent.
A6)
The general formula can be written as,
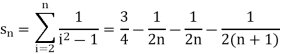
We get on applying limits,
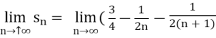 ) = 3/4
) = 3/4
This is the convergent series and its value is 3 / 4
Q7) Prove that the following series is convergent and find its sum.

A7)
Here,
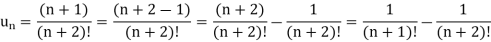
And


Hence the series is convergent and the limit is 1/2.
Q8) Test for absolute convergence:
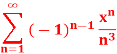
A8)
Let the series is  ,
,
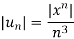
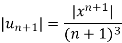
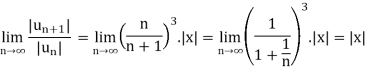
By ratio test,
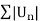 is convergent, if |x|<1.
is convergent, if |x|<1.
 is absolutely convergent if |x|< 1.
is absolutely convergent if |x|< 1.
Q9) Show that the series  is absolutely convergent.
is absolutely convergent.
A9)
We have,
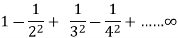
|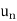 | =
| = 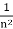 and |
and |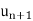 | =
| = 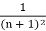
The first condition and second conditions are-
1. |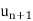 |<|
|<|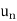 |
|
2. 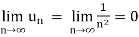
Both the conditions are satisfied.
So that we can say that by Leibnitz’s rule, the series is convergent.
The series is also convergent by p-test as p = 2 > 1.
Hence the given series is absolutely convergent.
Q10) Test the convergence/Divergence of the series:

A10)
Here the given series is alternately negative and positive, which is also a geometric infinite series.
1. Suppose,
S = 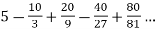
According to the conditions of geometric series,
Here, a = 5, and common ratio (r) = -2/3
Thus, we know that,
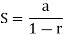
So,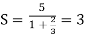
Sum of the series is finite, which is 3.
So, we can say that the given series is convergent.
Now.
Again, sum of the positive terms,
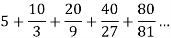
The series is geometric, then
A = 5 and r = 2/3, then
Sum of the series,

Sum of the series is finite then the series is convergent.
Both conditions are satisfied, then the given series is absolutely convergent.
Q11) Test the series for absolute/conditional convergence.
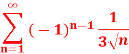
A11)
The given series is an alternating series of the form,
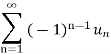
Here,
1.
2.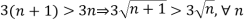

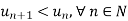
And,
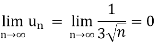
Hence bt Leibnitz’s test, the given series is convergent,
But,

Is divergent by p-series test.
So that, the given series is conditionally convergent.
Q12) Test the convergence of the series whose nth term is given below-
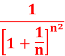
A12)

By root test 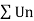 is convergent.
is convergent.
Q13) Test the convergence of the series whose nth term is given below-
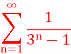
A13)
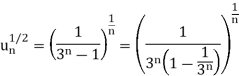
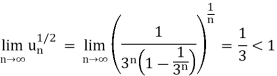
By root test 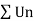 is convergent.
is convergent.
Q14) Test the convergence of the following series:
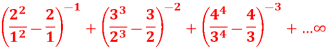
A14)
Here, we have,


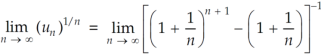
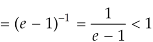
Therefore, the given series is convergent.
Q15) Test the convergence of the following series.

A15)
We have 
First, we will find  and the
and the 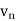

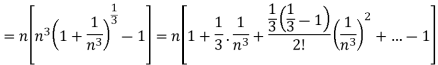
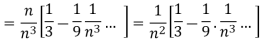
And



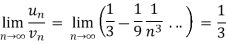
Here, we can see that, the limit is finite and not zero,
Therefore, 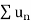 and
and  converges or diverges together.
converges or diverges together.
Since 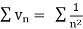 is of the form
is of the form  where p = 2>1
where p = 2>1
So that, we can say that,
 is convergent, so that
is convergent, so that 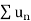 will also be convergent.
will also be convergent.
Q16) Show that the following series is convergent.

A16)
Here we have
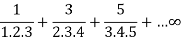
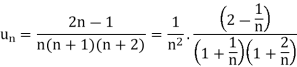
Suppose,
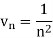


Which is finite and not zero.
By comparison test  and
and 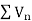 converge or diverge together.
converge or diverge together.
But,
Is convergent. So that 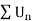 is also convergent.
is also convergent.
Q17) Test the convergence of the series whose n’th term is given below- n’th term = 
A17)
We have
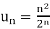 and
and 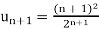
By D’Alembert ratio test,
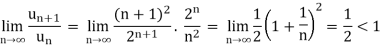
So that by D’Alembert ratio test, the series will be convergent.
Q18) Test for the convergence of the n’th term of the series given below-
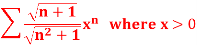
A18)
We have,
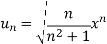

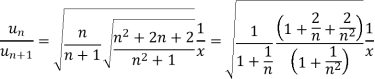
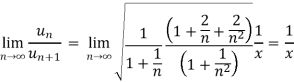
Now, by D’Alembert ratio test  converges if
converges if  and diverges if
and diverges if 
At x = 1, this test fails.
Now, when x = 1
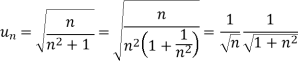



The limit is finite and not zero.
Then by comparison test, 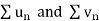 converges or diverges together.
converges or diverges together.
Since  is the form of
is the form of  , in which
, in which 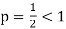
Hence  diverges then
diverges then 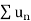 will also diverge.
will also diverge.
Therefore, in the given series 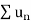 converges if x<1 and diverges if x≥1.
converges if x<1 and diverges if x≥1.