Unit - 3

Complex Variable (Differentiation)

Q1) What is De Moivre’s theorem?

A1)

Let Then by the product rule in polar form, we

Get

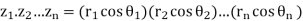
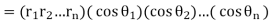
Thus

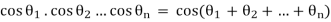
If we chose 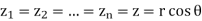then 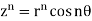or for choice of r = 1, we get

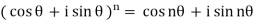
Which is known as De Moivre’s theorem.

Q2) Simplify-

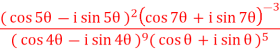
A2)

By using De-Moivre’s theorem:

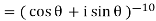
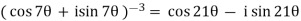
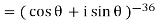
Substituting these values in given expression, we get

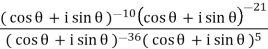
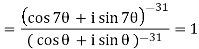
Q3) Find all the values of (-1 + i √3)3/2

A3)

Let

-1 + i√3 = x+iy, so x = - 1.

y = √3. Then r = √x2 + y2 = √1+3 = √4 = 2

-1 = x = r cos θ = 2 cos θ, so cos θ = - ½ 

√3 = y = r sin θ = 2 sin θ, so sin θ = √3/2

θ= π – π/3 = 2π/3. Thus

-1 + i √3 = reiθ = 2ei2π/3

Now

(-1 + i√3)3/2 = (2ei2π/3)3/2 = (8ei2π)1/2

= √8 ei(2π+2kπ/2) with k = 0, 1

= √8 eiπ = - √8 = -2√2 for k = 0

= √8 ei2π = + √8 = 2√2 for k = 1

Thus the solutions are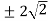

Q4) What are circular functions?

A4)

Euler’s exponential form of circular functions:

If

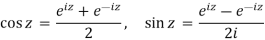
Q5) Prove that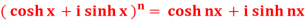

A5)

LHS =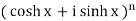

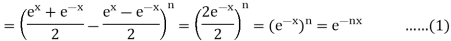
Now RHS

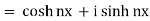
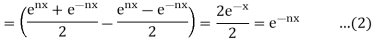
From (1) and (2), we have

LHS = RHS

Q6) What is complex function?

A6)

x + iy is a complex variable which is denoted by z

If for each value of the complex variable z = x + iy in a region R, we have one or more than one values of w = u + iv, then w is called a complex function of z.

And it is denoted as-

w = u(x , y) + iv(x , y) = f(z)

Neighbourhood of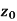

Let a point in the complex plane and z be any positive number, then the set of points z such that-

||<ε

Is called ε- neighbourhood of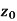

Q7) Find-

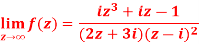
A7)

Here we have-

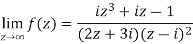
Divide numerator and denominator by , we get-

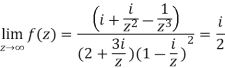
Q8) Show that f(z) = Re z = x is continuous but not differentiable.

A8)

Continuity:

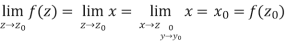
Not differentiability-

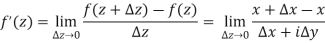
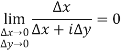
While

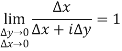
Hence limit does not exist which means function is not differentiable.

Q9) If w = log z, then find 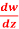. Also determine where w is non-analytic.

A9)

Here we have

Therefore-

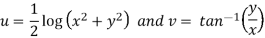
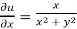and
 

Again-

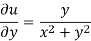
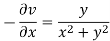
Hence the C-R conditions are satisfied also the partial derivatives are continuous except at (0 , 0).

So that w is analytic everywhere but not at z = 0

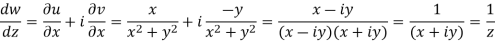
Q10) Prove that the function 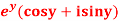is an analytical function.

A10)

Let 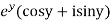=u+iv

Let 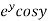=u and 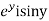=v

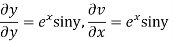
Hence C-R-Equation satisfied.

Q11) Prove that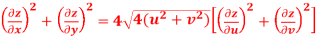

A11)

Given that

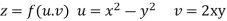
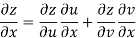
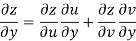
Since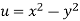      

V=2xy

Now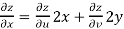

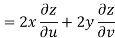
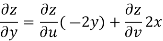
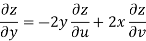
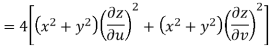
But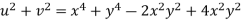                                      

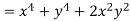
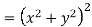
Hence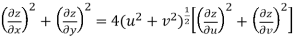 

Q12) Show that polar form of C-R equations are-

A12)

z = x + iy =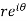

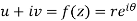
U and v are expressed in terms of r and θ.

Differentiate it partially w.r.t. r and θ, we get-

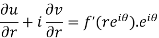
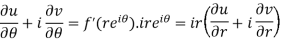
By equating real and imaginary parts, we get-

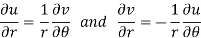
Q13) State and prove necessary condition for function f(z) to be analytic.

A13)

The necessary condition for a function 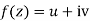to be analytic at all the points in a region R are

         (ii)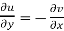

Provided,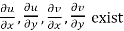

Proof:

Let 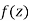be an analytic function in region R.

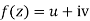
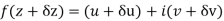
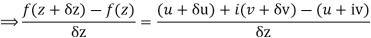
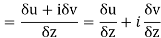
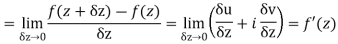
Along real axis

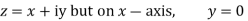
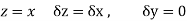
Then f’(z), becomes-

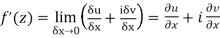      ………… (1)

Along imaginary axis

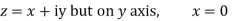
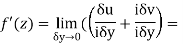
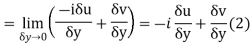
From equation (1) and (2)

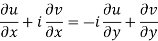
Equating real and imaginary parts

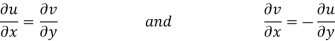
Therefore-

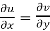and

These are called Cauchy Riemann Equations.

Q14) State and prove CR equations in polar form.

A14)

C-R equations in polar form are-

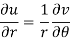
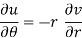
Proof:

As we know that-

x = r cos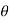 and u is the function of x and y

z = x + iy = r ( cos

Differentiate (1) partially with respect to r, we get-

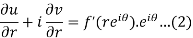
Now differentiate (1) with respect to , we get-

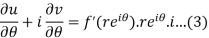
Substitute the value of 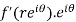, we get-

u/θ + iv/θ = r(u/r + i v/r)i                or     u/θ + i v/θ = ir u/r – r v/r

Equating real and imaginary parts, we get-

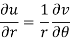
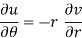
Proved

Q15) Prove that if f(z) = u + iv is an analytic function, then u and v are both harmonic functions.

A15)

Suppose f(z) = u + iv, be an analytic function, then we have 

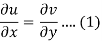
Differentiate (1) with respect to x, we get

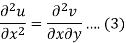
Differentiate (2) with respect to y, we get

Add 3 and 4-

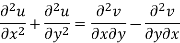
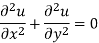
Similarly-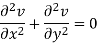
 

So that u and v are harmonic functions.

Q16) Prove that 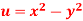and 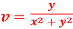are harmonic functions of (x, y).

A16)

We have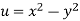

Now

u/x = 2x,    2u/x2 = 2,          u/y = -2y,           2u/y2 = -2

2u/x2 + 2u/y2 = 2-2 =0

Here it satisfies Laplace equation so that u (x, y) is harmonic.

Now-

v = y/x2 + y2,      v/x = - 2xy/ (x2 +y2)2

2v/x2 = (x2+y2)2(-2y) – (-2xy)2(x2+y2)2x / (x2+y2)4

= (x2+y2)(-2y)-(-2xy)4x / (x2 + y2)3 = 6x2y – 2y3 / (x2 + y2)3

v/y = (x2+y2). 1 – y(2y) / (x2+y2)2  = x2 – y2 / (x2 + y2)2

2v/y2 = (x2+y2)2 (-2y) - (x2-y2)2(x2+y2)(2y) / (x2+y2)4 = (x2+y2)(-2y)- (x2-y2)(4y) / (x2+y2)3

= -2x2y – 2y3 -4x2y +4y3 / (x2 + y2)3 = -6x2y + 2y3/(x2 + y2)3

On adding the above results-

We get-

So that v(x, y) is also a harmonic function.

Q17) If

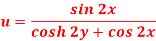
Then find f(z)

A17)

Here-

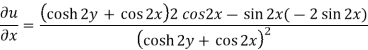
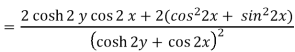
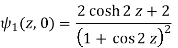
u/y = - sin 2x(2 sinh 2y) / (cosh 2y + cos 2x)2 = -2sin 2x sinh 2y / (cosh 2y + cos 2x)2 = 2(x, y)

ψ2(z, 0) = 0

f(z) = [ψ1(z, 0) – i ψ2 (z, 0)] dz + C

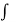= (2cos 2z + 2)/ (1+cos 2z)2 dz + C = 2 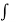1/ 1+ cos 2z  dz + C

= 2 1/ 2 cos2z dz + C = 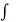sec2 z dz + C = tan z + C

Which is the required answer.

Q18) Verify if 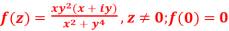is analytic or not?

A18)

Here we have-

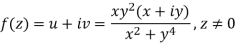
And

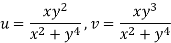
At origin-

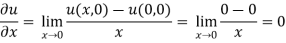
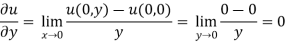
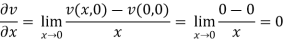
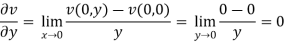
Since

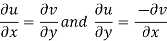
C-R equations are satisfied at the origin-

But-

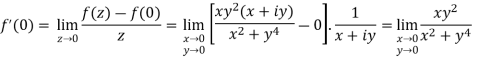
Let 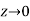along the real axis y = 0, then

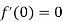
Now let along the curve , then-

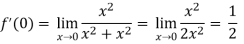
Which shows that f'(0) does not exist since the limit is not unique along two different paths. Hence f(z) is not analytic at origin but C-R equations are satisfied.