Unit - 1
Higher order linear differential equations and applications
Q1) Solve 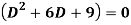
A1) Its auxiliary equation is-
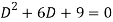
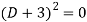
Where-
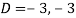
Therefore the complete solution is-
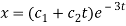
Q2) What is inverse operator?
A2)
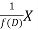 is that function of x, not containing arbitrary constants which when operated upon gives X.
is that function of x, not containing arbitrary constants which when operated upon gives X.
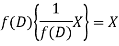
So that  satisfies the equation f(D)y = X and is, therefore, its P.I.
satisfies the equation f(D)y = X and is, therefore, its P.I.
f(D) and 1/f(D) are inverse operator.
Note-
1. 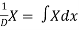
2. 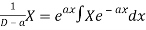
Q3) Find the P.I. Of (D + 2)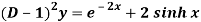
A3)
P.I. = 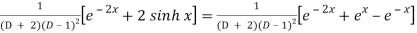
Now we will evaluate each term separately-
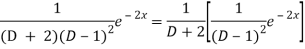
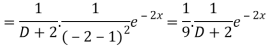
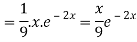
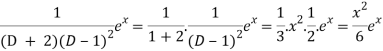
And
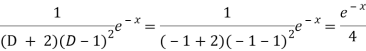
Therefore-
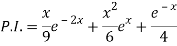
Q4) Solve (D – D’ – 2 ) (D – D’ – 3) z = 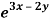
A4)
The C.F. Will be given by-
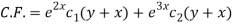
Particular integral-
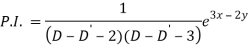
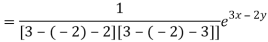
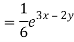
Therefore the complete solution is-
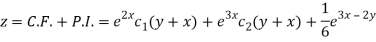
Q5) Find the P.I. Of 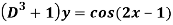
A5)
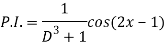

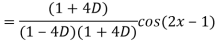

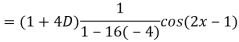
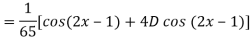
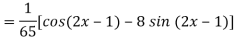
Q6) Find the P.I. Of (D + 1) (D + D’ – 1)z = sin (x + 2y)
A6)
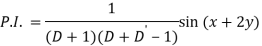
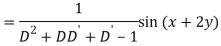
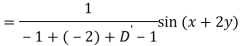
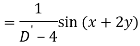
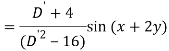
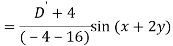

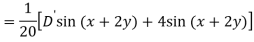
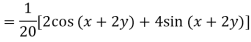
Q7) Find P.I. Of
A7)
P.I = 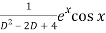
Replace D by D+1

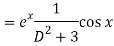
Put 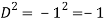
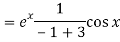

Q8) Solve 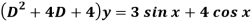
A8)
Here first we will find the C.F.-
Its auxiliary equation will be-
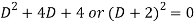
Here we get-
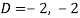
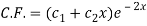
Now we will find P.I.-
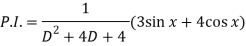
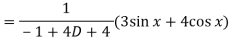
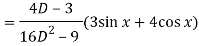

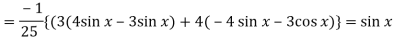
Now the complete solution is-
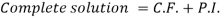
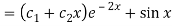
Q9) Solve the following DE by using variation of parameters-
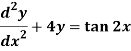
A9)
We can write the given equation in symbolic form as-
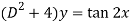
To find CF-
It’s A.E. Is 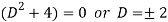
So that CF is- 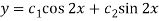
To find PI-
Here 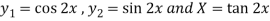
Now 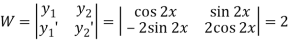
Thus PI = 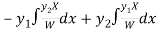
= 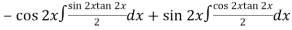
= 
= 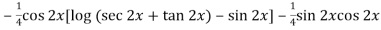
= 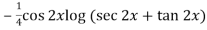
So that the complete solution is-

Q10) Solve the following by using the method of variation of parameters.
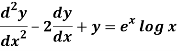
A10)
This can be written as-
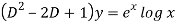
C.F.-
Auxiliary equation is- 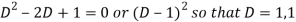
So that the C.F. Will be- 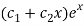
P.I.-
Here 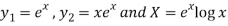
Now 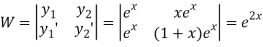
Thus PI = 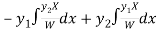
= 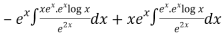
= 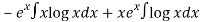
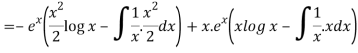

So that the complete solution is-
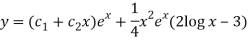
Q11) Solve
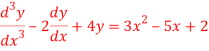
A11)
The Auxiliary equation is 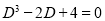

 The C.F is
The C.F is 
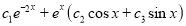
P.I 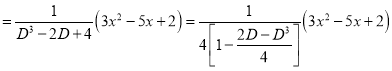
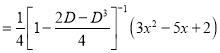
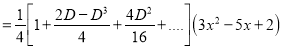
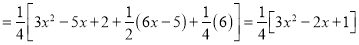
 The Complete Solution is
The Complete Solution is 
Q12) Solve 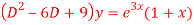
A12)
The auxiliary equation is 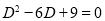
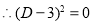
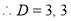
 The C.F is
The C.F is
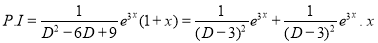
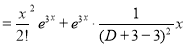

But 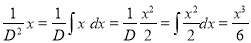
 The Complete Solution is
The Complete Solution is 
Q13) Solve (4D² +4D -3)y = 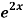
A13)
Auxiliary equation is 4m² +4m – 3 = 0
We get, (2m+3)(2m – 1) = 0
m = 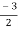 ,
, 
Complementary function: CF is A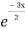 + B
+ B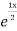
Now we will find particular integral,
P.I. =  f(x)
f(x)
= 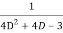 .
. 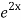
= 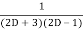 .
. 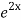
= 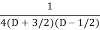 .
. 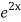
= 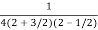 .
. 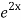 =
= 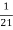 .
. 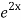
General solution is y = CF + PI
= A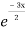 + B
+ B .
. 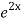
Q14) Solve 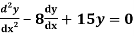
A14)
Given, 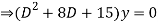
Here Auxiliary equation is
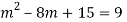
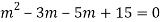
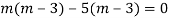
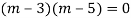
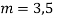
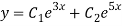
Q15) Solve 
A15)
Auxiliary equation are 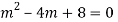
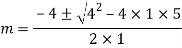
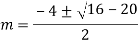
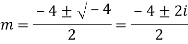
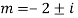
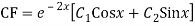
Q16) 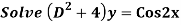
A16)
Auxiliary equation are 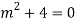

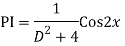
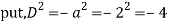
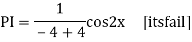
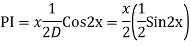
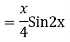
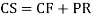
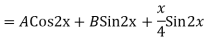
Q17) Solve 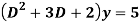
A17)
The AE is 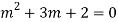
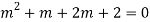

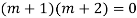
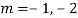
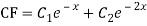
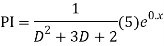
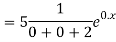
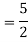
Complete solution = CF + PI

Q18) Find the PI of 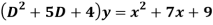
A18)

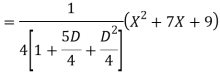

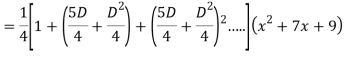
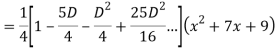
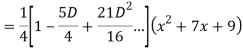
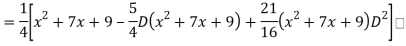
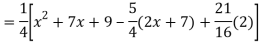

Q19) Solve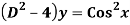
A19)
The AE is 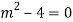
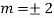
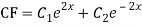
We know, 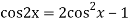
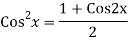
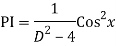
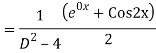
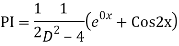
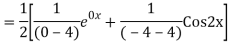
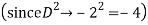
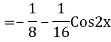
Complete solution is y= CF + PI
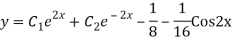
Q20) 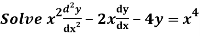
A20)
Putting, 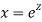


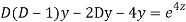
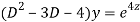
AE is 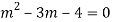
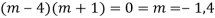
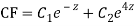


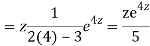
CS = CF + PI
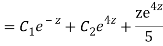
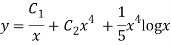
Q21) Finding the optimal current of an electrical circuit(RL circuits) in which the initial
Condition is i=0 at t=0
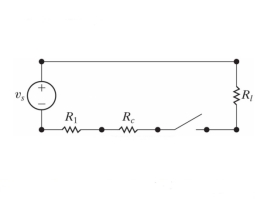
A21)
By Kirchhoff voltage law(KVL) method, we get
The differential equation for the RL circuit will be 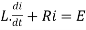
In which initial conditions are i=0 at t=0
The standard form of the equation is,
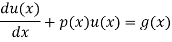
Dividing the differential equation by L to obtain
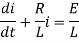
The integrating factor is
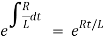
Multiplying the above equation with standard form gives rise to
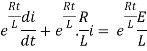
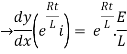
By applying integration on both sides we get
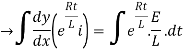
Now applying i=0 at t-0 gives us
0=
 C=-
C=-
NOW
i=
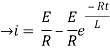
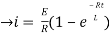 = t
= t 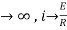
Therefore by finding current of the RL circuits is i=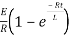
Hence we complete the solution by first order differential equation of first order and even several types of networking circuits and fluid mechanics uses this method.
Unit - 1
Higher order linear differential equations and applications
Q1) Solve 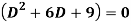
A1) Its auxiliary equation is-
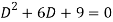

Where-
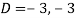
Therefore the complete solution is-
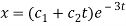
Q2) What is inverse operator?
A2)
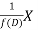 is that function of x, not containing arbitrary constants which when operated upon gives X.
is that function of x, not containing arbitrary constants which when operated upon gives X.
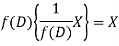
So that 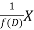 satisfies the equation f(D)y = X and is, therefore, its P.I.
satisfies the equation f(D)y = X and is, therefore, its P.I.
f(D) and 1/f(D) are inverse operator.
Note-
1. 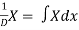
2. 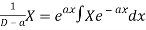
Q3) Find the P.I. Of (D + 2)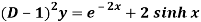
A3)
P.I. = 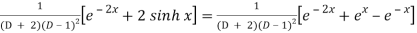
Now we will evaluate each term separately-
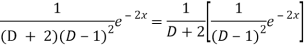
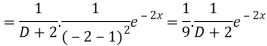
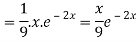
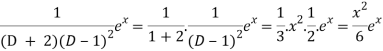
And
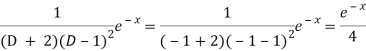
Therefore-
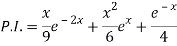
Q4) Solve (D – D’ – 2 ) (D – D’ – 3) z = 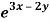
A4)
The C.F. Will be given by-
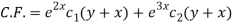
Particular integral-
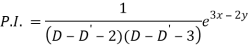
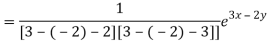
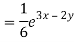
Therefore the complete solution is-

Q5) Find the P.I. Of 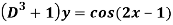
A5)
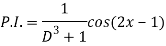

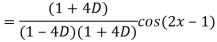
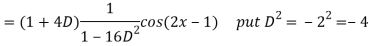
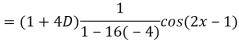
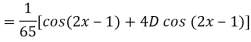
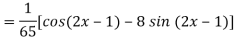
Q6) Find the P.I. Of (D + 1) (D + D’ – 1)z = sin (x + 2y)
A6)

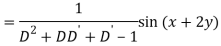

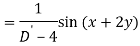

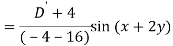
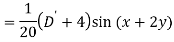

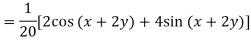
Q7) Find P.I. Of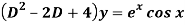
A7)
P.I = 
Replace D by D+1
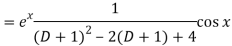
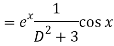
Put 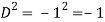
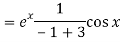
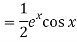
Q8) Solve 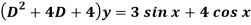
A8)
Here first we will find the C.F.-
Its auxiliary equation will be-
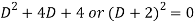
Here we get-
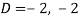

Now we will find P.I.-
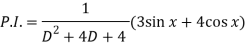
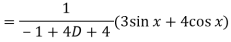
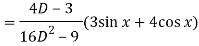
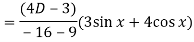
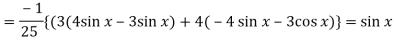
Now the complete solution is-
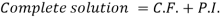
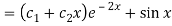
Q9) Solve the following DE by using variation of parameters-
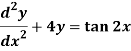
A9)
We can write the given equation in symbolic form as-
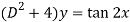
To find CF-
It’s A.E. Is 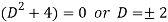
So that CF is- 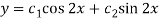
To find PI-
Here 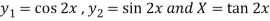
Now 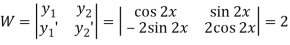
Thus PI = 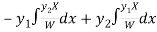
= 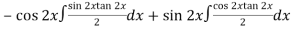
= 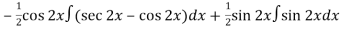
= 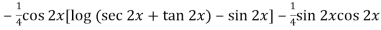
= 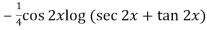
So that the complete solution is-
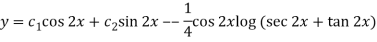
Q10) Solve the following by using the method of variation of parameters.
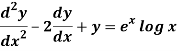
A10)
This can be written as-
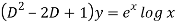
C.F.-
Auxiliary equation is- 
So that the C.F. Will be- 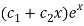
P.I.-
Here 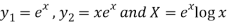
Now 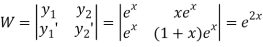
Thus PI = 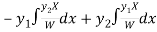
= 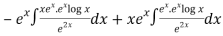
= 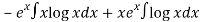
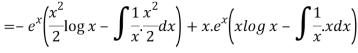
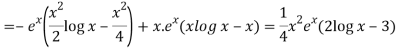
So that the complete solution is-
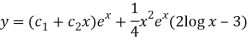
Q11) Solve

A11)
The Auxiliary equation is 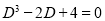
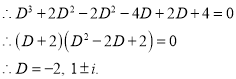
 The C.F is
The C.F is 
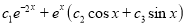
P.I 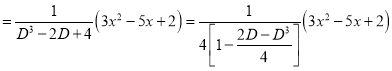
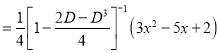
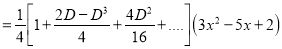

 The Complete Solution is
The Complete Solution is 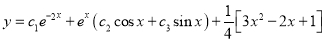
Q12) Solve 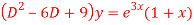
A12)
The auxiliary equation is 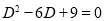
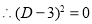
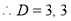
 The C.F is
The C.F is
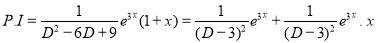
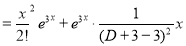
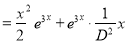
But 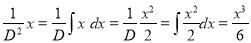
 The Complete Solution is
The Complete Solution is 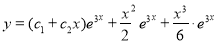
Q13) Solve (4D² +4D -3)y = 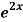
A13)
Auxiliary equation is 4m² +4m – 3 = 0
We get, (2m+3)(2m – 1) = 0
m = 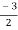 ,
, 
Complementary function: CF is A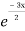 + B
+ B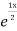
Now we will find particular integral,
P.I. = 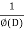 f(x)
f(x)
=  .
. 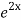
= 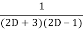 .
. 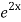
= 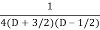 .
. 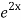
= 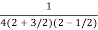 .
. 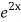 =
= 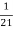 .
. 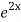
General solution is y = CF + PI
= A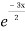 + B
+ B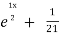 .
. 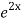
Q14) Solve 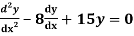
A14)
Given, 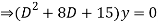
Here Auxiliary equation is
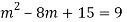
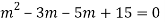
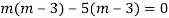

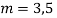
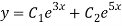
Q15) Solve 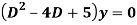
A15)
Auxiliary equation are 
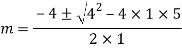
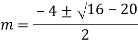

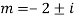

Q16) 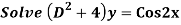
A16)
Auxiliary equation are 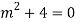
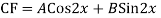
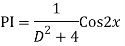
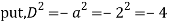
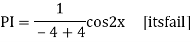
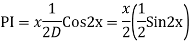
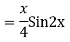
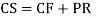
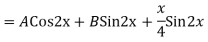
Q17) Solve 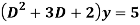
A17)
The AE is 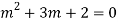
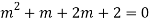
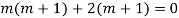
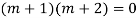
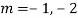
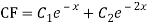
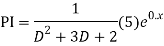
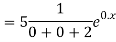
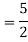
Complete solution = CF + PI
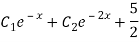
Q18) Find the PI of 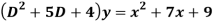
A18)
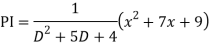
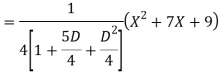
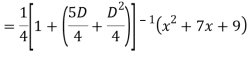
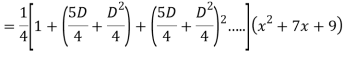
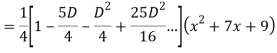

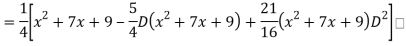

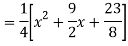
Q19) Solve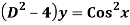
A19)
The AE is 

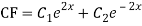
We know, 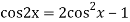
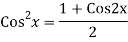
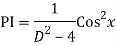
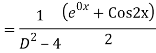
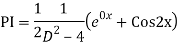
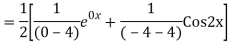
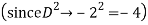
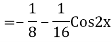
Complete solution is y= CF + PI
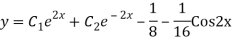
Q20) 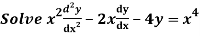
A20)
Putting, 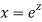
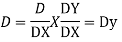
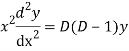
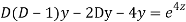
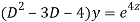
AE is 
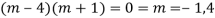
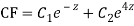
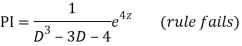
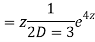
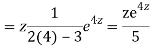
CS = CF + PI

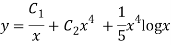
Q21) Finding the optimal current of an electrical circuit(RL circuits) in which the initial
Condition is i=0 at t=0
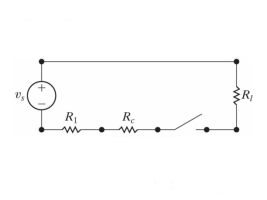
A21)
By Kirchhoff voltage law(KVL) method, we get
The differential equation for the RL circuit will be 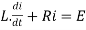
In which initial conditions are i=0 at t=0
The standard form of the equation is,
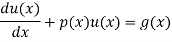
Dividing the differential equation by L to obtain

The integrating factor is
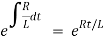
Multiplying the above equation with standard form gives rise to
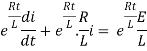
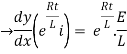
By applying integration on both sides we get
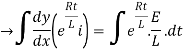
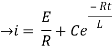
Now applying i=0 at t-0 gives us
0=
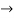 C=-
C=-
NOW
i=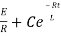

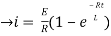 = t
= t 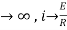
Therefore by finding current of the RL circuits is i=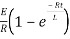
Hence we complete the solution by first order differential equation of first order and even several types of networking circuits and fluid mechanics uses this method.
Unit - 1
Higher order linear differential equations and applications
Q1) Solve 
A1) Its auxiliary equation is-
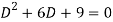
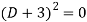
Where-
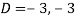
Therefore the complete solution is-
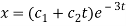
Q2) What is inverse operator?
A2)
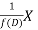 is that function of x, not containing arbitrary constants which when operated upon gives X.
is that function of x, not containing arbitrary constants which when operated upon gives X.
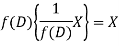
So that  satisfies the equation f(D)y = X and is, therefore, its P.I.
satisfies the equation f(D)y = X and is, therefore, its P.I.
f(D) and 1/f(D) are inverse operator.
Note-
1. 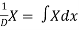
2. 
Q3) Find the P.I. Of (D + 2)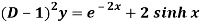
A3)
P.I. = 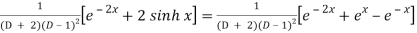
Now we will evaluate each term separately-
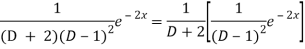

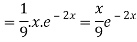
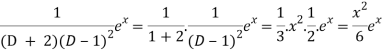
And
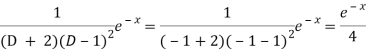
Therefore-
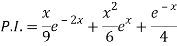
Q4) Solve (D – D’ – 2 ) (D – D’ – 3) z = 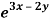
A4)
The C.F. Will be given by-
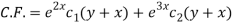
Particular integral-
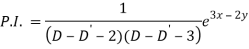
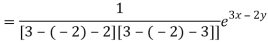
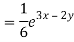
Therefore the complete solution is-
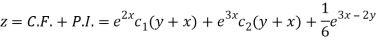
Q5) Find the P.I. Of 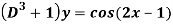
A5)
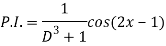


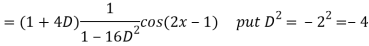
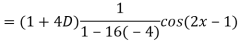
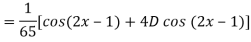
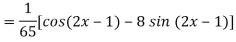
Q6) Find the P.I. Of (D + 1) (D + D’ – 1)z = sin (x + 2y)
A6)

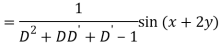
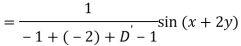
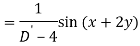
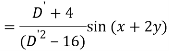
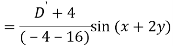
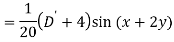
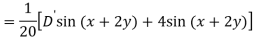

Q7) Find P.I. Of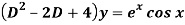
A7)
P.I = 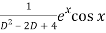
Replace D by D+1
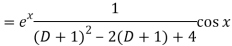
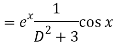
Put 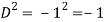
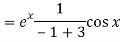
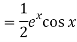
Q8) Solve 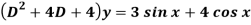
A8)
Here first we will find the C.F.-
Its auxiliary equation will be-
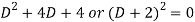
Here we get-
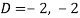
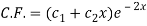
Now we will find P.I.-
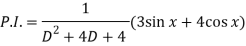
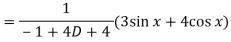
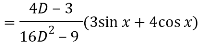

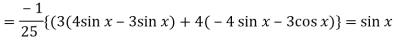
Now the complete solution is-
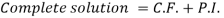
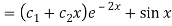
Q9) Solve the following DE by using variation of parameters-
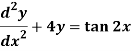
A9)
We can write the given equation in symbolic form as-
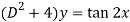
To find CF-
It’s A.E. Is 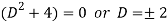
So that CF is- 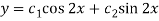
To find PI-
Here 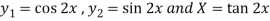
Now 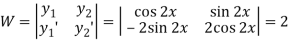
Thus PI = 
= 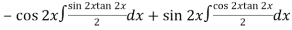
= 
= 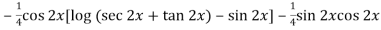
= 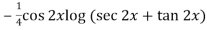
So that the complete solution is-
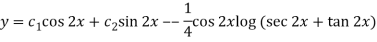
Q10) Solve the following by using the method of variation of parameters.
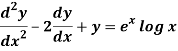
A10)
This can be written as-
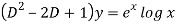
C.F.-
Auxiliary equation is- 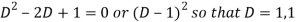
So that the C.F. Will be- 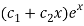
P.I.-
Here 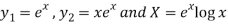
Now 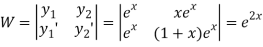
Thus PI = 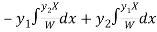
= 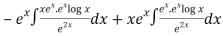
= 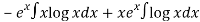

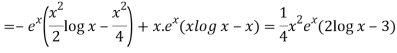
So that the complete solution is-
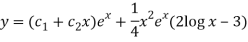
Q11) Solve
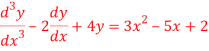
A11)
The Auxiliary equation is 
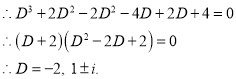
 The C.F is
The C.F is 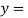
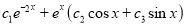
P.I 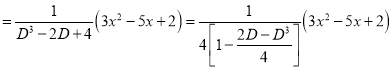
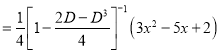
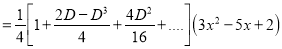
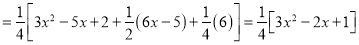
 The Complete Solution is
The Complete Solution is 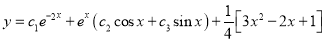
Q12) Solve 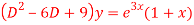
A12)
The auxiliary equation is 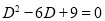
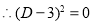
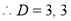
 The C.F is
The C.F is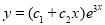
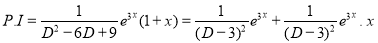
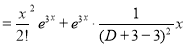
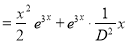
But 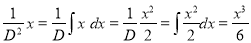
 The Complete Solution is
The Complete Solution is 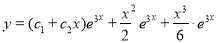
Q13) Solve (4D² +4D -3)y = 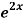
A13)
Auxiliary equation is 4m² +4m – 3 = 0
We get, (2m+3)(2m – 1) = 0
m = 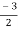 ,
, 
Complementary function: CF is A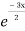 + B
+ B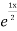
Now we will find particular integral,
P.I. = 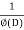 f(x)
f(x)
= 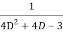 .
. 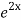
= 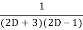 .
. 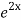
= 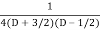 .
. 
= 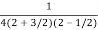 .
. 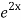 =
= 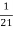 .
. 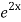
General solution is y = CF + PI
= A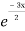 + B
+ B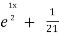 .
. 
Q14) Solve 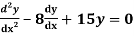
A14)
Given, 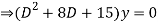
Here Auxiliary equation is
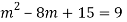
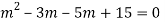
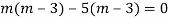
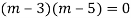
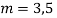
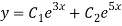
Q15) Solve 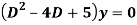
A15)
Auxiliary equation are 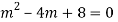
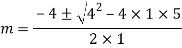


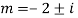
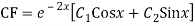
Q16) 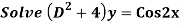
A16)
Auxiliary equation are 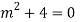
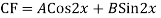
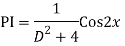
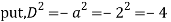
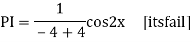
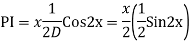
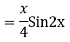
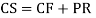
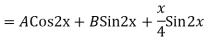
Q17) Solve 
A17)
The AE is 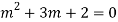
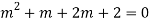
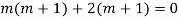
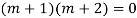

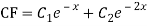
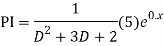
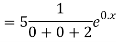
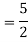
Complete solution = CF + PI
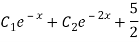
Q18) Find the PI of 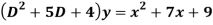
A18)
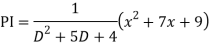
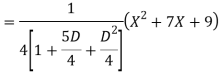
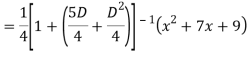
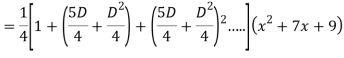
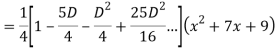
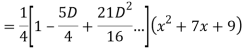
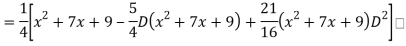
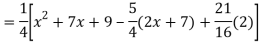
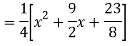
Q19) Solve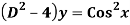
A19)
The AE is 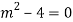


We know, 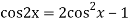
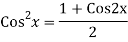
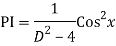

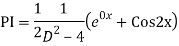
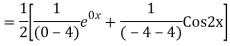
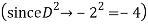
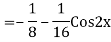
Complete solution is y= CF + PI
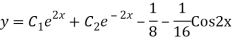
Q20) 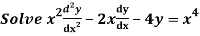
A20)
Putting, 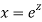
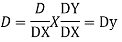

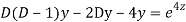
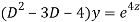
AE is 
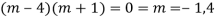
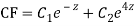
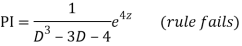

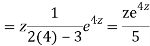
CS = CF + PI
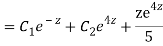
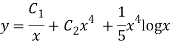
Q21) Finding the optimal current of an electrical circuit(RL circuits) in which the initial
Condition is i=0 at t=0
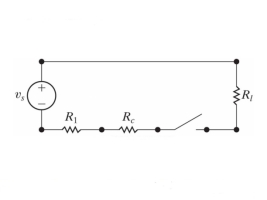
A21)
By Kirchhoff voltage law(KVL) method, we get
The differential equation for the RL circuit will be 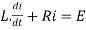
In which initial conditions are i=0 at t=0
The standard form of the equation is,
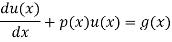
Dividing the differential equation by L to obtain
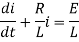
The integrating factor is
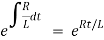
Multiplying the above equation with standard form gives rise to
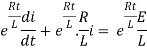
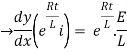
By applying integration on both sides we get
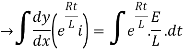
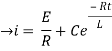
Now applying i=0 at t-0 gives us
0=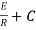
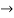 C=-
C=-
NOW
i=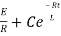
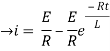
 = t
= t 
Therefore by finding current of the RL circuits is i=
Hence we complete the solution by first order differential equation of first order and even several types of networking circuits and fluid mechanics uses this method.
Unit - 1
Higher order linear differential equations and applications
Q1) Solve 
A1) Its auxiliary equation is-
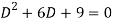
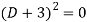
Where-
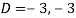
Therefore the complete solution is-
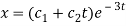
Q2) What is inverse operator?
A2)
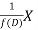 is that function of x, not containing arbitrary constants which when operated upon gives X.
is that function of x, not containing arbitrary constants which when operated upon gives X.
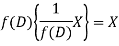
So that  satisfies the equation f(D)y = X and is, therefore, its P.I.
satisfies the equation f(D)y = X and is, therefore, its P.I.
f(D) and 1/f(D) are inverse operator.
Note-
1. 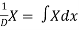
2. 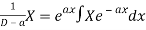
Q3) Find the P.I. Of (D + 2)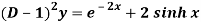
A3)
P.I. = 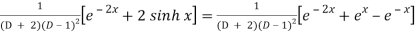
Now we will evaluate each term separately-
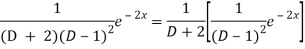

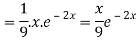
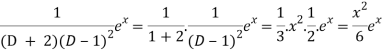
And
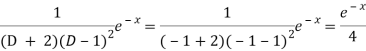
Therefore-
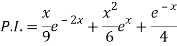
Q4) Solve (D – D’ – 2 ) (D – D’ – 3) z = 
A4)
The C.F. Will be given by-
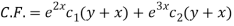
Particular integral-
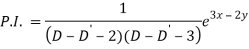
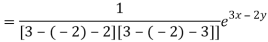
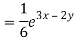
Therefore the complete solution is-
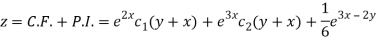
Q5) Find the P.I. Of 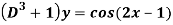
A5)
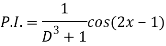

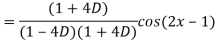
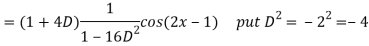
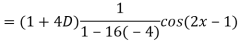
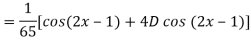

Q6) Find the P.I. Of (D + 1) (D + D’ – 1)z = sin (x + 2y)
A6)
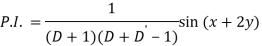
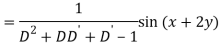
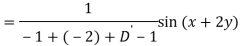
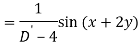
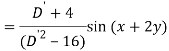
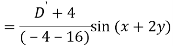

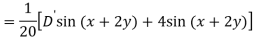
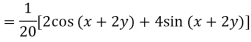
Q7) Find P.I. Of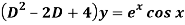
A7)
P.I = 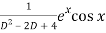
Replace D by D+1
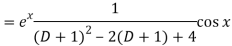
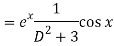
Put 
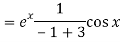
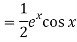
Q8) Solve 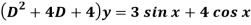
A8)
Here first we will find the C.F.-
Its auxiliary equation will be-
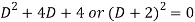
Here we get-
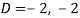
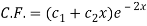
Now we will find P.I.-

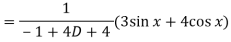
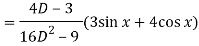
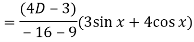
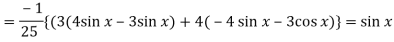
Now the complete solution is-
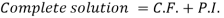
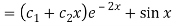
Q9) Solve the following DE by using variation of parameters-
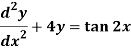
A9)
We can write the given equation in symbolic form as-

To find CF-
It’s A.E. Is 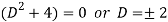
So that CF is- 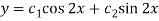
To find PI-
Here 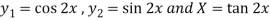
Now 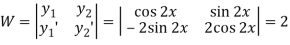
Thus PI = 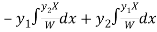
= 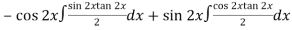
= 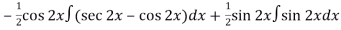
= 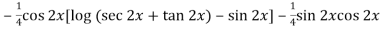
= 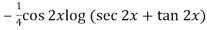
So that the complete solution is-
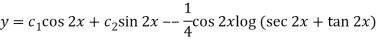
Q10) Solve the following by using the method of variation of parameters.
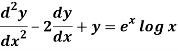
A10)
This can be written as-
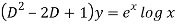
C.F.-
Auxiliary equation is- 
So that the C.F. Will be- 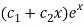
P.I.-
Here 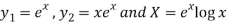
Now 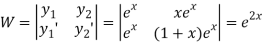
Thus PI = 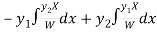
= 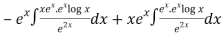
= 
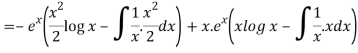
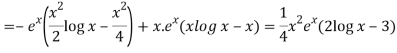
So that the complete solution is-
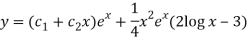
Q11) Solve
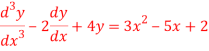
A11)
The Auxiliary equation is 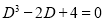
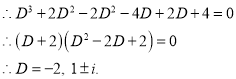
 The C.F is
The C.F is 
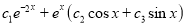
P.I 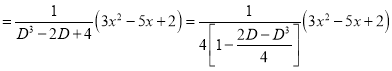
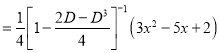
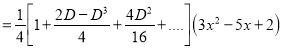

 The Complete Solution is
The Complete Solution is 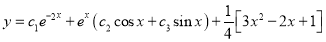
Q12) Solve 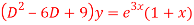
A12)
The auxiliary equation is 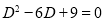

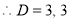
 The C.F is
The C.F is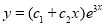
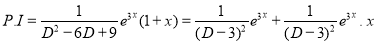
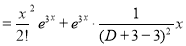
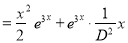
But 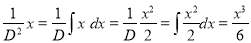
 The Complete Solution is
The Complete Solution is 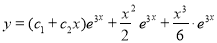
Q13) Solve (4D² +4D -3)y = 
A13)
Auxiliary equation is 4m² +4m – 3 = 0
We get, (2m+3)(2m – 1) = 0
m = 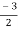 ,
, 
Complementary function: CF is A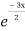 + B
+ B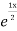
Now we will find particular integral,
P.I. = 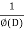 f(x)
f(x)
= 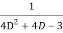 .
. 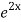
= 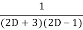 .
. 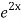
= 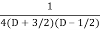 .
. 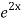
=  .
. 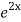 =
= 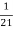 .
. 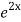
General solution is y = CF + PI
= A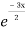 + B
+ B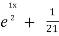 .
. 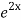
Q14) Solve 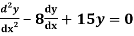
A14)
Given, 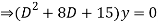
Here Auxiliary equation is
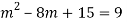
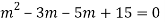

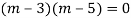
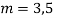
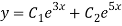
Q15) Solve 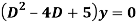
A15)
Auxiliary equation are 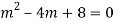
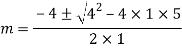
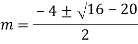
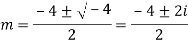
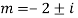
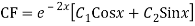
Q16) 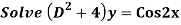
A16)
Auxiliary equation are 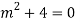
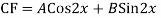
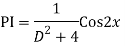

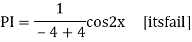
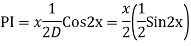
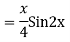
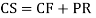
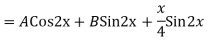
Q17) Solve 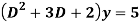
A17)
The AE is 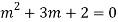
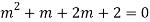
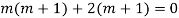
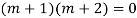
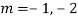
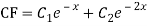
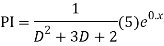
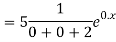
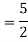
Complete solution = CF + PI
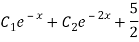
Q18) Find the PI of 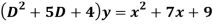
A18)
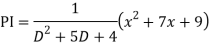
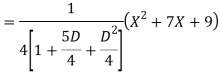
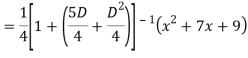
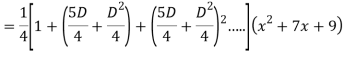
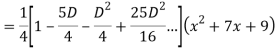
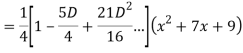
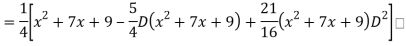
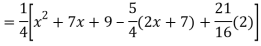
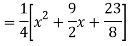
Q19) Solve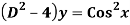
A19)
The AE is 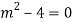
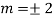
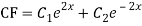
We know, 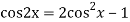
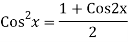
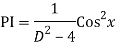
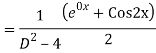
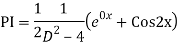

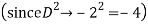
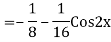
Complete solution is y= CF + PI
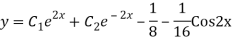
Q20) 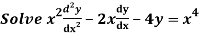
A20)
Putting, 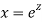
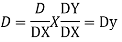
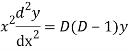
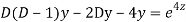
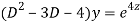
AE is 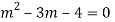
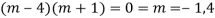
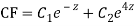
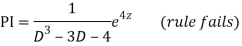
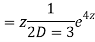
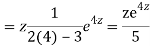
CS = CF + PI
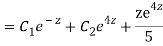
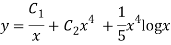
Q21) Finding the optimal current of an electrical circuit(RL circuits) in which the initial
Condition is i=0 at t=0

A21)
By Kirchhoff voltage law(KVL) method, we get
The differential equation for the RL circuit will be 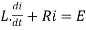
In which initial conditions are i=0 at t=0
The standard form of the equation is,
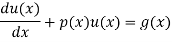
Dividing the differential equation by L to obtain
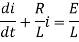
The integrating factor is
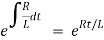
Multiplying the above equation with standard form gives rise to
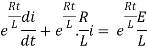
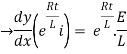
By applying integration on both sides we get
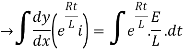
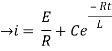
Now applying i=0 at t-0 gives us
0=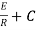
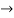 C=-
C=-
NOW
i=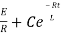
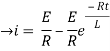
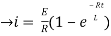 = t
= t 
Therefore by finding current of the RL circuits is i=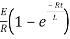
Hence we complete the solution by first order differential equation of first order and even several types of networking circuits and fluid mechanics uses this method.