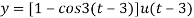Unit – 4
Laplace transform
Q1) Define Laplace and inverse Laplace transforms.
A1)
Let f(t) be any function of t defined for all positive values of t. Then the Laplace transform of the function f(t) is defined as-
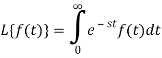
Provided that the integral exists, here ‘s’ is the parameter which could be real or complex.
The inverse of the Laplace transform can be defined as below-
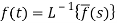
Here 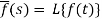
f(t) is called the inverse Laplace transform of 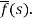
L is called the Laplace transformation operator.
Q2) What are the advantages of Laplace transform?
A2)
Advantages of LT:
1. With the application of Laplace transform, particular solution of differential equation (D.E.) is obtained directly without the necessity of first determining general solution and then obtaining the particular solution (by substitution of initial conditions).
2. L.T. Solves non-homogeneous D.E. Without the necessity of first solving the corresponding homogeneous D.E.
3. L.T. Is applicable not only to continuous functions but also to piecewise continuous functions, complicated periodic functions, step functions and impulse functions.
Q3) Find the Laplace transform of 
A3)
Here 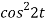
So that we can write it as-
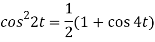
Now-

Q4) Find the Laplace transform of (1 + cos 2t)
A4)
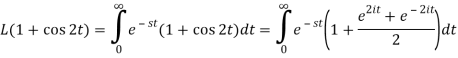
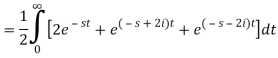
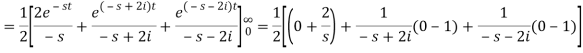
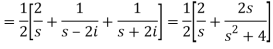
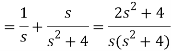
So that-
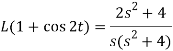
Q5) Find 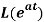
A5)
By the definition of Laplace transform-
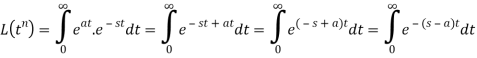
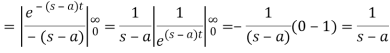
Q6) Prove that 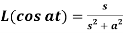 .
.
A6)
Here we know that,
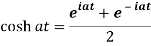
So that-
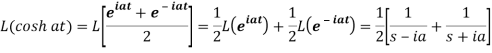
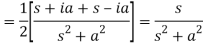
Q7) What is the linearity property of LT?
A7)
Linearity property-
Let a and b be any two constants and  ,
, 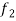 any two functions of t, then-
any two functions of t, then-
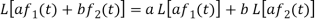
Proof: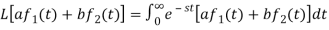

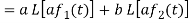
Hence proved.
Q8) Find the Laplace transform of t sin at.
A8)
Here-


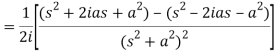
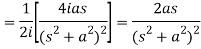
Q9) Find the Laplace transform of the following function-
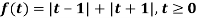
A9)
The given function f(t) can be written as-
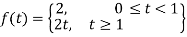
So that, by definition,
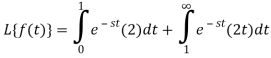
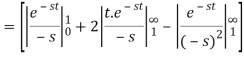
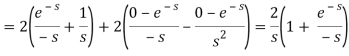
Q10) Find-
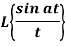
Given that,
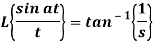
A10)
By using change of scale property-
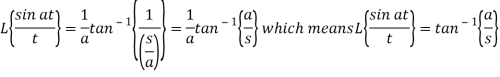
Q11) What do you understand by the Laplace transform of integral of f(t)?
A11)
Laplace transform of integral of f(t) -
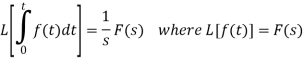
Proof: Suppose
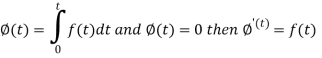
We know that-
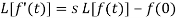
So that-
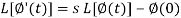
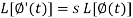
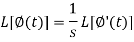
Putting the values of  and
and  , we get-
, we get-

Q12) Find the Laplace transform of 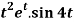 .
.
A12)
Here-
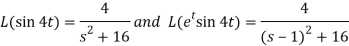
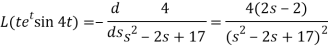
Now-
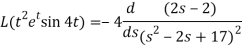
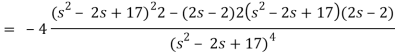
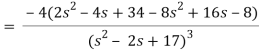
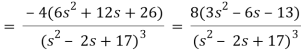
Q13) Find the Laplace transform of the function f(t) = 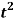 using the theorem of transform of derivative.
using the theorem of transform of derivative.
A13)
f (0) = 0, f ‘(0) = 0, f’’ (t ) = 2
By theorem
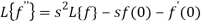
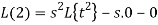
So that
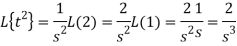
Q14) Find the inverse Laplace transform of the following:
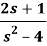
A14)
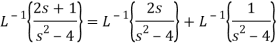
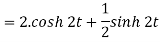
Q15) Find the inverse LT of
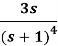
A15)
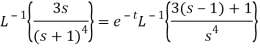
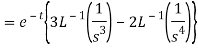
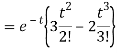
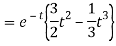
Q16) Find the inverse Laplace transform of-
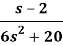
A16)
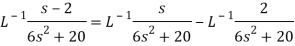
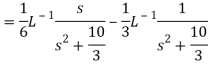

Q17) Find the Laplace inverse of-
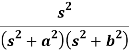
A17)
We will convert the function into partial fractions-
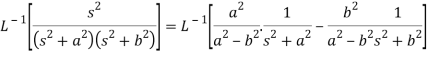
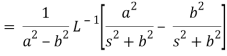
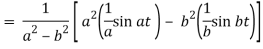
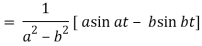
Q18) Find the inverse LT of-

A18)
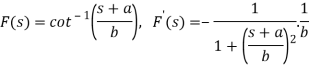
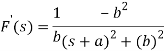
So that
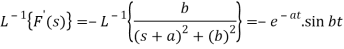
Since

Thus
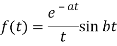
Q19) Evaluate the following-
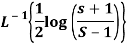
A19)
Here

We know that
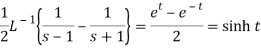
Thus applying inverse LT of integrals, we get
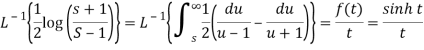
Q20) Apply convolution theorem to evaluate-
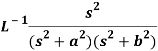
A20)
Since
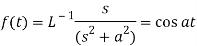
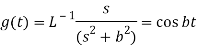
By convolution theorem, we get-
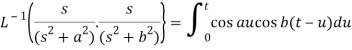
Because- f(u) = cos au, g(t-u) = cos b(t – u)

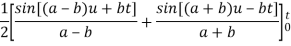
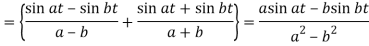
Q21) Use Laplace transform method to solve the following equation-
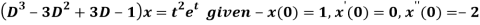
A21)
Here, taking the Laplace transform of both sides, we get

It becomes-
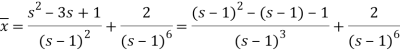
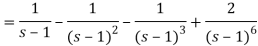
On inversion, we get-
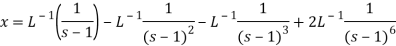
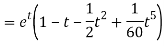
Q22) Find the solution of the initial value problem by using Laplace transform-
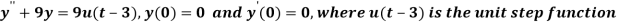
A22)
Here we have-
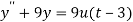
Taking Laplace transform, we get-
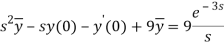
Putting the given values, we get-
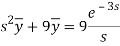
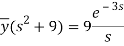

On inversion, we get-


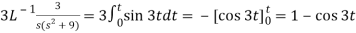 4
4
Now-
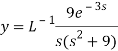
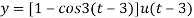
Unit – 4
Laplace transform
Q1) Define Laplace and inverse Laplace transforms.
A1)
Let f(t) be any function of t defined for all positive values of t. Then the Laplace transform of the function f(t) is defined as-
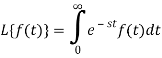
Provided that the integral exists, here ‘s’ is the parameter which could be real or complex.
The inverse of the Laplace transform can be defined as below-
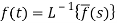
Here 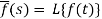
f(t) is called the inverse Laplace transform of 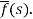
L is called the Laplace transformation operator.
Q2) What are the advantages of Laplace transform?
A2)
Advantages of LT:
1. With the application of Laplace transform, particular solution of differential equation (D.E.) is obtained directly without the necessity of first determining general solution and then obtaining the particular solution (by substitution of initial conditions).
2. L.T. Solves non-homogeneous D.E. Without the necessity of first solving the corresponding homogeneous D.E.
3. L.T. Is applicable not only to continuous functions but also to piecewise continuous functions, complicated periodic functions, step functions and impulse functions.
Q3) Find the Laplace transform of 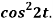
A3)
Here 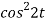
So that we can write it as-

Now-

Q4) Find the Laplace transform of (1 + cos 2t)
A4)
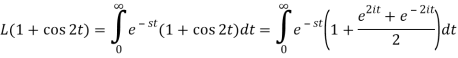
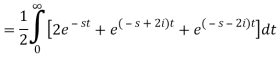
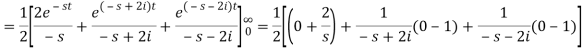

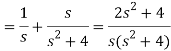
So that-

Q5) Find 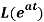
A5)
By the definition of Laplace transform-
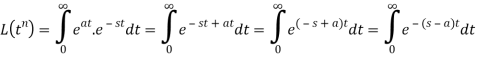

Q6) Prove that 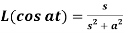 .
.
A6)
Here we know that,
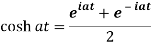
So that-
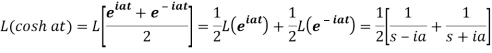
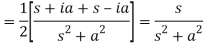
Q7) What is the linearity property of LT?
A7)
Linearity property-
Let a and b be any two constants and 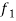 ,
, 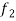 any two functions of t, then-
any two functions of t, then-
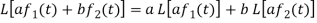
Proof: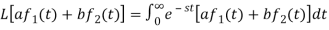
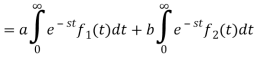
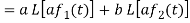
Hence proved.
Q8) Find the Laplace transform of t sin at.
A8)
Here-
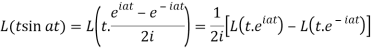
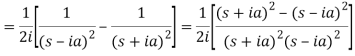
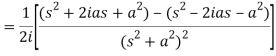
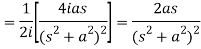
Q9) Find the Laplace transform of the following function-
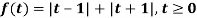
A9)
The given function f(t) can be written as-
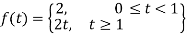
So that, by definition,
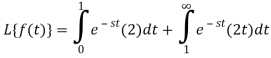
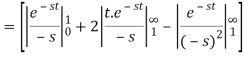

Q10) Find-
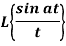
Given that,
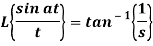
A10)
By using change of scale property-

Q11) What do you understand by the Laplace transform of integral of f(t)?
A11)
Laplace transform of integral of f(t) -
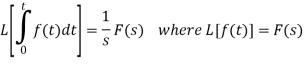
Proof: Suppose
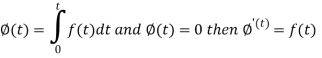
We know that-
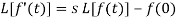
So that-
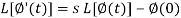
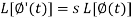
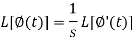
Putting the values of 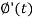 and
and 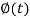 , we get-
, we get-
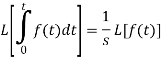
Q12) Find the Laplace transform of 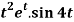 .
.
A12)
Here-
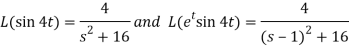
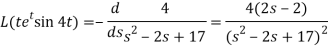
Now-
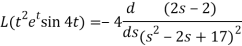
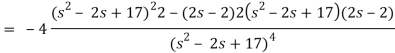
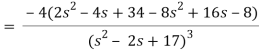
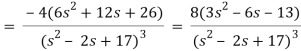
Q13) Find the Laplace transform of the function f(t) = 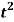 using the theorem of transform of derivative.
using the theorem of transform of derivative.
A13)
f (0) = 0, f ‘(0) = 0, f’’ (t ) = 2
By theorem
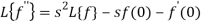
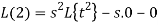
So that
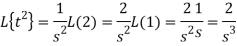
Q14) Find the inverse Laplace transform of the following:
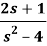
A14)
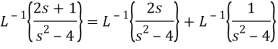
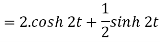
Q15) Find the inverse LT of
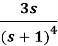
A15)
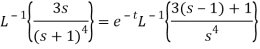
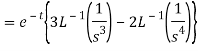
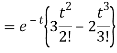
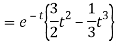
Q16) Find the inverse Laplace transform of-
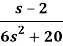
A16)

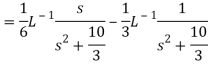
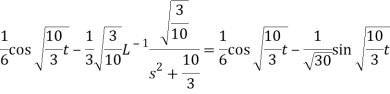
Q17) Find the Laplace inverse of-

A17)
We will convert the function into partial fractions-

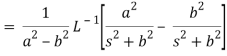
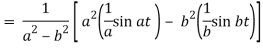
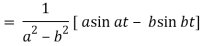
Q18) Find the inverse LT of-
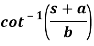
A18)
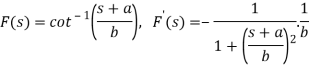

So that

Since
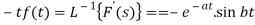
Thus
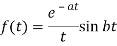
Q19) Evaluate the following-
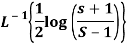
A19)
Here

We know that
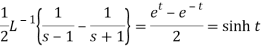
Thus applying inverse LT of integrals, we get
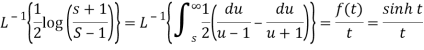
Q20) Apply convolution theorem to evaluate-
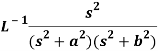
A20)
Since
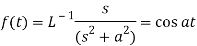
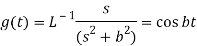
By convolution theorem, we get-
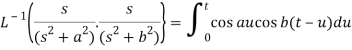
Because- f(u) = cos au, g(t-u) = cos b(t – u)
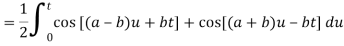
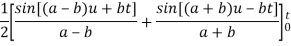
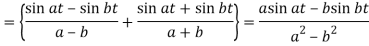
Q21) Use Laplace transform method to solve the following equation-
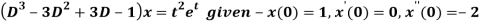
A21)
Here, taking the Laplace transform of both sides, we get
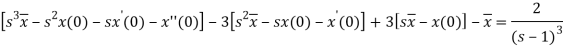
It becomes-
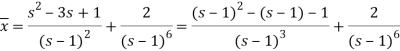
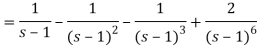
On inversion, we get-
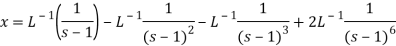
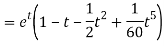
Q22) Find the solution of the initial value problem by using Laplace transform-
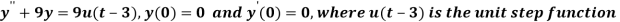
A22)
Here we have-
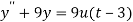
Taking Laplace transform, we get-
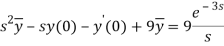
Putting the given values, we get-
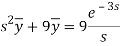
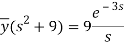
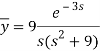
On inversion, we get-
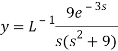
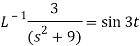
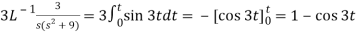 4
4
Now-
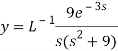

Unit – 4
Laplace transform
Q1) Define Laplace and inverse Laplace transforms.
A1)
Let f(t) be any function of t defined for all positive values of t. Then the Laplace transform of the function f(t) is defined as-
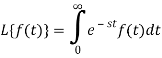
Provided that the integral exists, here ‘s’ is the parameter which could be real or complex.
The inverse of the Laplace transform can be defined as below-
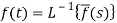
Here 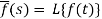
f(t) is called the inverse Laplace transform of 
L is called the Laplace transformation operator.
Q2) What are the advantages of Laplace transform?
A2)
Advantages of LT:
1. With the application of Laplace transform, particular solution of differential equation (D.E.) is obtained directly without the necessity of first determining general solution and then obtaining the particular solution (by substitution of initial conditions).
2. L.T. Solves non-homogeneous D.E. Without the necessity of first solving the corresponding homogeneous D.E.
3. L.T. Is applicable not only to continuous functions but also to piecewise continuous functions, complicated periodic functions, step functions and impulse functions.
Q3) Find the Laplace transform of 
A3)
Here 
So that we can write it as-
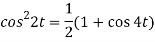
Now-
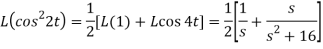
Q4) Find the Laplace transform of (1 + cos 2t)
A4)
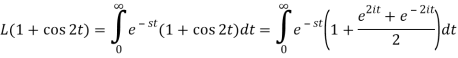
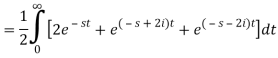
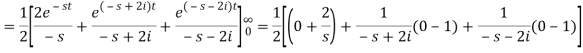
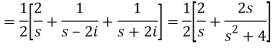
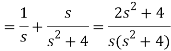
So that-

Q5) Find 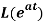
A5)
By the definition of Laplace transform-

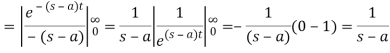
Q6) Prove that  .
.
A6)
Here we know that,

So that-
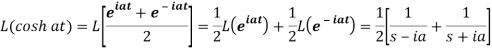
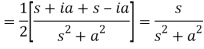
Q7) What is the linearity property of LT?
A7)
Linearity property-
Let a and b be any two constants and  ,
, 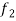 any two functions of t, then-
any two functions of t, then-
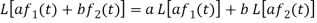
Proof: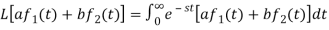
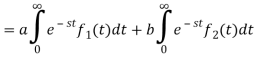

Hence proved.
Q8) Find the Laplace transform of t sin at.
A8)
Here-

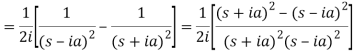
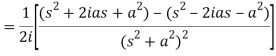
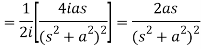
Q9) Find the Laplace transform of the following function-
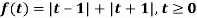
A9)
The given function f(t) can be written as-
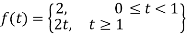
So that, by definition,
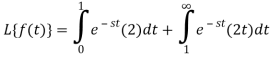
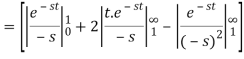
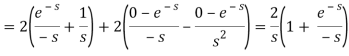
Q10) Find-
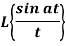
Given that,

A10)
By using change of scale property-

Q11) What do you understand by the Laplace transform of integral of f(t)?
A11)
Laplace transform of integral of f(t) -
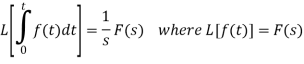
Proof: Suppose
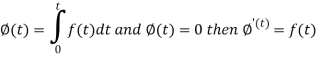
We know that-
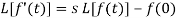
So that-
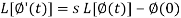
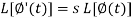
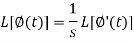
Putting the values of 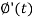 and
and 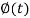 , we get-
, we get-
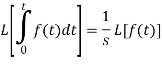
Q12) Find the Laplace transform of 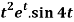 .
.
A12)
Here-
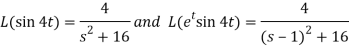
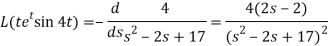
Now-
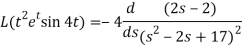
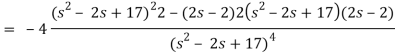
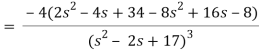
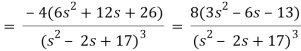
Q13) Find the Laplace transform of the function f(t) = 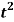 using the theorem of transform of derivative.
using the theorem of transform of derivative.
A13)
f (0) = 0, f ‘(0) = 0, f’’ (t ) = 2
By theorem
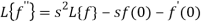
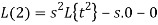
So that
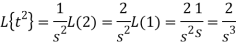
Q14) Find the inverse Laplace transform of the following:
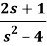
A14)
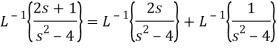
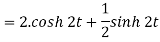
Q15) Find the inverse LT of
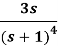
A15)
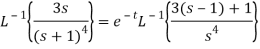
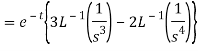
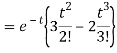
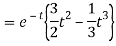
Q16) Find the inverse Laplace transform of-
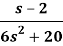
A16)
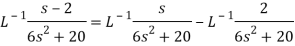

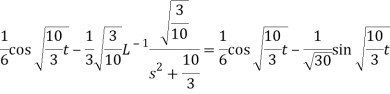
Q17) Find the Laplace inverse of-
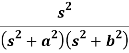
A17)
We will convert the function into partial fractions-
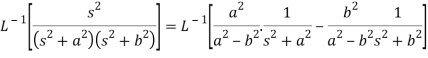
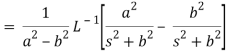
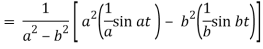
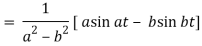
Q18) Find the inverse LT of-
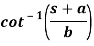
A18)
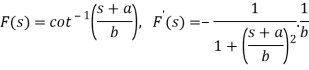
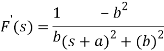
So that

Since
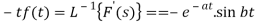
Thus
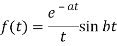
Q19) Evaluate the following-

A19)
Here
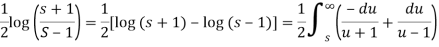
We know that
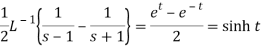
Thus applying inverse LT of integrals, we get

Q20) Apply convolution theorem to evaluate-
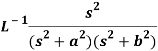
A20)
Since

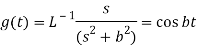
By convolution theorem, we get-
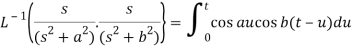
Because- f(u) = cos au, g(t-u) = cos b(t – u)
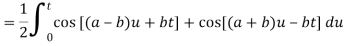
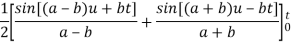

Q21) Use Laplace transform method to solve the following equation-
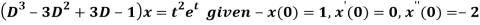
A21)
Here, taking the Laplace transform of both sides, we get
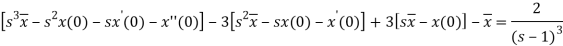
It becomes-
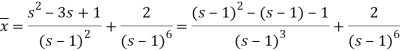
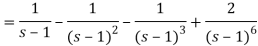
On inversion, we get-
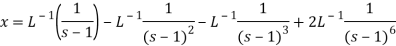

Q22) Find the solution of the initial value problem by using Laplace transform-
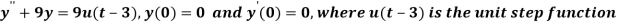
A22)
Here we have-
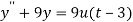
Taking Laplace transform, we get-
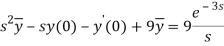
Putting the given values, we get-
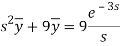
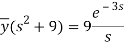
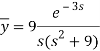
On inversion, we get-
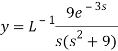
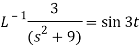
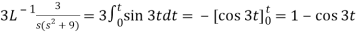 4
4
Now-
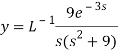
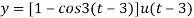
Unit – 4
Laplace transform
Q1) Define Laplace and inverse Laplace transforms.
A1)
Let f(t) be any function of t defined for all positive values of t. Then the Laplace transform of the function f(t) is defined as-

Provided that the integral exists, here ‘s’ is the parameter which could be real or complex.
The inverse of the Laplace transform can be defined as below-
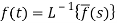
Here 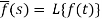
f(t) is called the inverse Laplace transform of 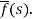
L is called the Laplace transformation operator.
Q2) What are the advantages of Laplace transform?
A2)
Advantages of LT:
1. With the application of Laplace transform, particular solution of differential equation (D.E.) is obtained directly without the necessity of first determining general solution and then obtaining the particular solution (by substitution of initial conditions).
2. L.T. Solves non-homogeneous D.E. Without the necessity of first solving the corresponding homogeneous D.E.
3. L.T. Is applicable not only to continuous functions but also to piecewise continuous functions, complicated periodic functions, step functions and impulse functions.
Q3) Find the Laplace transform of 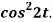
A3)
Here 
So that we can write it as-
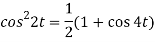
Now-

Q4) Find the Laplace transform of (1 + cos 2t)
A4)
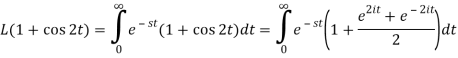
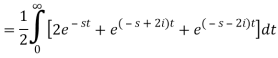
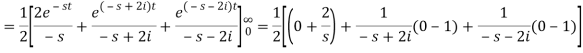
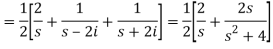
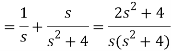
So that-
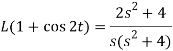
Q5) Find 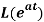
A5)
By the definition of Laplace transform-
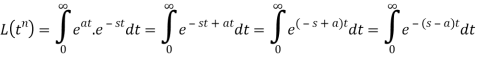
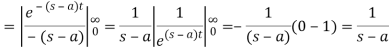
Q6) Prove that 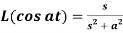 .
.
A6)
Here we know that,
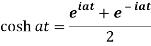
So that-
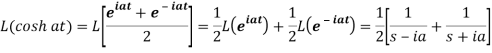
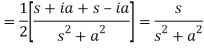
Q7) What is the linearity property of LT?
A7)
Linearity property-
Let a and b be any two constants and 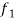 ,
, 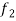 any two functions of t, then-
any two functions of t, then-

Proof: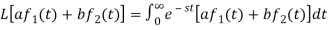
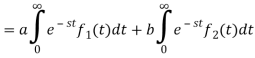
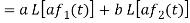
Hence proved.
Q8) Find the Laplace transform of t sin at.
A8)
Here-
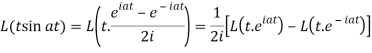
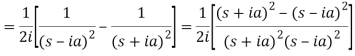
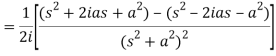
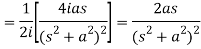
Q9) Find the Laplace transform of the following function-
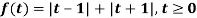
A9)
The given function f(t) can be written as-
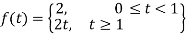
So that, by definition,
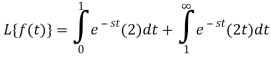
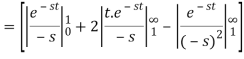
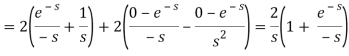
Q10) Find-
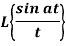
Given that,
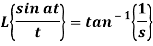
A10)
By using change of scale property-
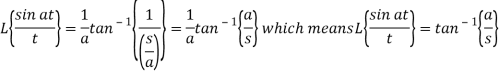
Q11) What do you understand by the Laplace transform of integral of f(t)?
A11)
Laplace transform of integral of f(t) -
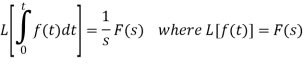
Proof: Suppose
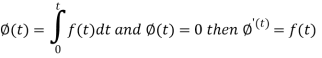
We know that-
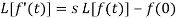
So that-

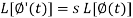
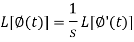
Putting the values of 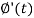 and
and 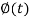 , we get-
, we get-
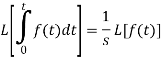
Q12) Find the Laplace transform of 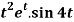 .
.
A12)
Here-
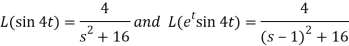
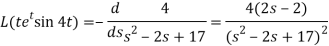
Now-
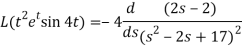
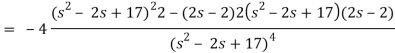
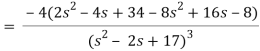
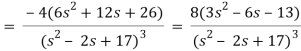
Q13) Find the Laplace transform of the function f(t) = 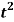 using the theorem of transform of derivative.
using the theorem of transform of derivative.
A13)
f (0) = 0, f ‘(0) = 0, f’’ (t ) = 2
By theorem
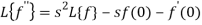
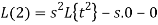
So that
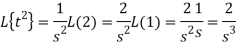
Q14) Find the inverse Laplace transform of the following:
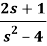
A14)
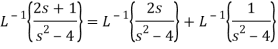
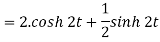
Q15) Find the inverse LT of
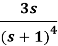
A15)
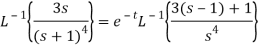
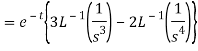
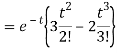
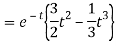
Q16) Find the inverse Laplace transform of-
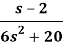
A16)
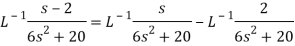
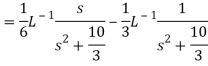
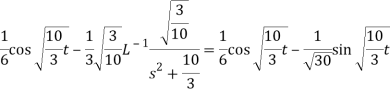
Q17) Find the Laplace inverse of-

A17)
We will convert the function into partial fractions-
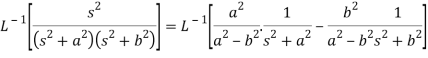
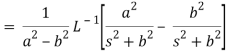
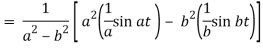
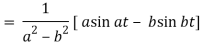
Q18) Find the inverse LT of-
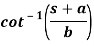
A18)
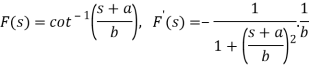
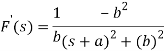
So that
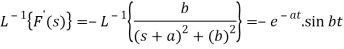
Since
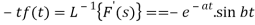
Thus
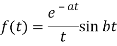
Q19) Evaluate the following-
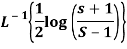
A19)
Here
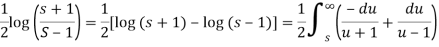
We know that
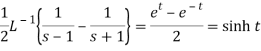
Thus applying inverse LT of integrals, we get
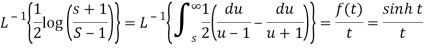
Q20) Apply convolution theorem to evaluate-

A20)
Since
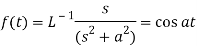
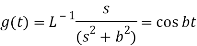
By convolution theorem, we get-

Because- f(u) = cos au, g(t-u) = cos b(t – u)
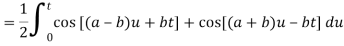
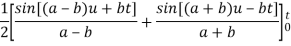
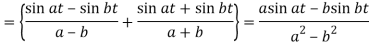
Q21) Use Laplace transform method to solve the following equation-
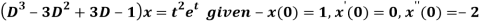
A21)
Here, taking the Laplace transform of both sides, we get
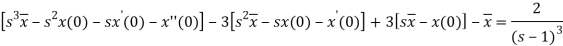
It becomes-
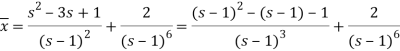
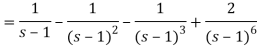
On inversion, we get-
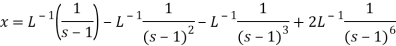
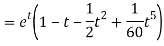
Q22) Find the solution of the initial value problem by using Laplace transform-
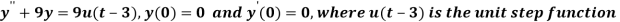
A22)
Here we have-
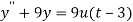
Taking Laplace transform, we get-
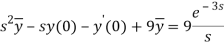
Putting the given values, we get-
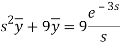
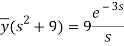
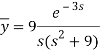
On inversion, we get-
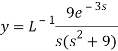
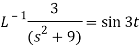
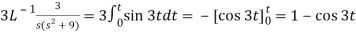 4
4
Now-