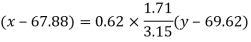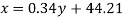Unit – 5
Statistics
Q1) Find the straight line that best fits of the following data by using method of least square.
X | 1 | 2 | 3 | 4 | 5 |
y | 14 | 27 | 40 | 55 | 68 |
A1)
Suppose the straight line
y = a + bx…….. (1)
Fits the best-
Then-
x | y | Xy | 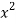 |
1 | 14 | 14 | 1 |
2 | 27 | 54 | 4 |
3 | 40 | 120 | 9 |
4 | 55 | 220 | 16 |
5 | 68 | 340 | 25 |
Sum = 15 | 204 | 748 | 55 |
Normal equations are-
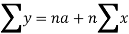
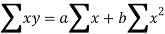
Put the values from the table, we get two normal equations-
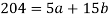
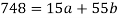
On solving the above equations, we get-
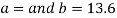
So that the best fit line will be- (on putting the values of a and b in equation (1))
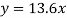
Q2) Find the best values of a and b so that y = a + bx fits the data given in the table
X | 0 | 1 | 2 | 3 | 4 |
Y | 1.0 | 2.9 | 4.8 | 6.7 | 8.6 |
A2)
y = a + bx
x | y | Xy | 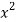 |
0 | 1.0 | 0 | 0 |
1 | 2.9 | 2.0 | 1 |
2 | 4.8 | 9.6 | 4 |
3 | 6.7 | 20.1 | 9 |
4 | 8.6 | 13.4 | 16 |
 |  | 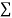 | 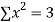 |
Normal equations, 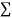 y= na+ b
y= na+ b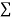 x (2)
x (2)
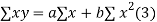
On putting the values of 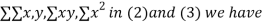
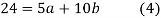
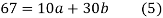
On solving (4) and (5) we get,
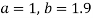
On substituting the values of a and b in (1) we get
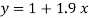
Q3) Fit a second degree parabola to the following data by least squares method.
 | 1929 | 1930 | 1931 | 1932 | 1933 | 1934 | 1935 | 1936 | 1937 |
 | 352 | 356 | 357 | 358 | 360 | 361 | 361 | 360 | 359 |
A3)
Taking x0 = 1933, y0 = 357
Taking u = x – x0, v = y – y0
u = x – 1933, v = y – 357
The equation y = a+bx+cx2 is transformed to v = A + Bu + Cu2 …(2)
 | u = x – 1933 | 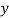 |  | 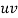 | 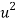 | u2v | u3 | u4 |
1929 | -4 | 352 | -5 | 20 | 16 | -80 | -64 | 256 |
1930 | -3 | 360 | -1 | 3 | 9 | -9 | -27 | 81 |
1931 | -2 | 357 | 0 | 0 | 4 | 0 | -8 | 16 |
1932 | -1 | 358 | 1 | -1 | 1 | 1 | -1 | 1 |
1933 | 0 | 360 | 3 | 0 | 0 | 0 | 0 | 0 |
1934 | 1 | 361 | 4 | 4 | 1 | 4 | 1 | 1 |
1935 | 2 | 361 | 4 | 8 | 4 | 16 | 8 | 16 |
1936 | 3 | 360 | 3 | 9 | 9 | 27 | 27 | 81 |
1937 | 4 | 359 | 2 | 8 | 16 | 32 | 64 | 256 |
Total | 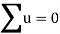 |
| 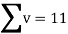 | 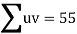 | 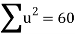 | 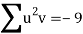 | 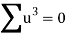 | 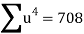 |
Normal equations are
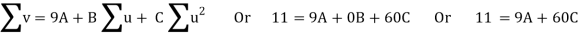

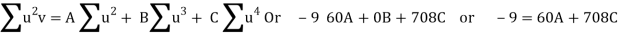
On solving these equations, we get A = 694/231, B = 17/20, C = - 247/924
V = 694/231 + 17/20 u – 247/924 u2V = 694/231 + 17/20 u – 247/924 u2
y – 357 = 694/231 + 17/20 (x – 1933) – 247/924 (x – 1933)2
= 694/231 + 17x/20 - 32861/20 – 247x2/924 (-3866x) – 247/924 + (1933)2
y = 694/231 – 32861/20 – 247/924 (1933)2 + 17x/20 + (247 3866)x/924 - 247 x2/924
y = 3 – 1643.05 – 998823.36 + 357 + 0.85 x + 1033.44 x – 0.267 x2
y = - 1000106.41 + 1034.29x – 0.267 x2
Q4) Find the least squares approximation of second degree for the discrete data
x | 2 | -1 | 0 | 1 | 2 |
y | 15 | 1 | 1 | 3 | 19 |
A4)
Let the equation of second degree polynomial be 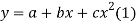
x | y | Xy | 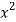 | 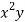 | 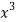 | 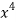 |
-2 | 15 | -30 | 4 | 60 | -8 | 16 |
-1 | 1 | -1 | 1 | 1 | -1 | 1 |
0 | 1 | 0 | 0 | 0 | 0 | 0 |
1 | 3 | 3 | 1 | 3 | 1 | 1 |
2 | 19 | 38 | 4 | 76 | 8 | 16 |
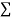 | 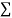 | 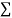 | 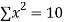 | 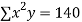 | 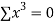 | 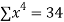 |
Normal equations are 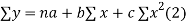
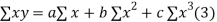
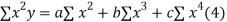
On putting the values of 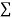 x,
x, 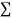 y,
y,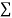 xy,
xy, 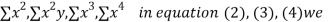 have
have
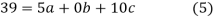
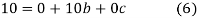
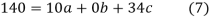
On solving (5),(6),(7), we get, 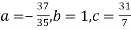
The required polynomial of second degree is
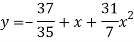
Q5) Fit a second degree parabola to the following data.
X = 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
Y = 1.1 | 1.3 | 1.6 | 2.0 | 2.7 | 3.4 | 4.1 |
A5)
We shift the origin to (2.5, 0) antique 0.5 as the new unit. This amounts to changing the variable x to X, by the relation X = 2x – 5.
Let the parabola of fit be y = a + bX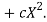 The values of
The values of 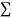 X etc. Are calculated as below:
X etc. Are calculated as below:
x | X | y | Xy | 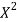 | 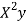 | 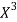 | 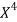 |
1.0 | -3 | 1.1 | -3.3 | 9 | 9.9 | -27 | 81 |
1.5 | -2 | 1.3 | -2.6 | 4 | 5.2 | -5 | 16 |
2.0 | -1 | 1.6 | -1.6 | 1 | 1.6 | -1 | 1 |
2.5 | 0 | 2.0 | 0.0 | 0 | 0.0 | 0 | 0 |
3.0 | 1 | 2.7 | 2.7 | 1 | 2.7 | 1 | 1 |
3.5 | 2 | 3.4 | 6.8 | 4 | 13.6 | 8 | 16 |
4.0 | 3 | 4.1 | 12.3 | 9 | 36.9 | 27 | 81 |
Total | 0 | 16.2 | 14.3 | 28 | 69.9 | 0 | 196 |
The normal equations are
7a + 28c =16.2; 28b =14.3;. 28a +196c=69.9
Solving these as simultaneous equations we get
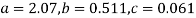
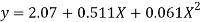
Replacing X bye 2x – 5 in the above equation we get
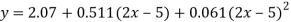
Which simplifies to y =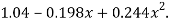
This is the required parabola of the best fit.
Q6) Fit the curve 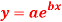 by using the method of least square.
by using the method of least square.
X | 1 | 2 | 3 | 4 | 5 | 6 |
Y | 7.209 | 5.265 | 3.846 | 2.809 | 2.052 | 1.499 |
A6)
Here-
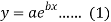
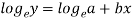
Now put-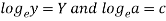
Then we get-
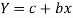
x | Y | 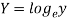 | XY | 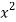 |
1 | 7.209 | 1.97533 | 1.97533 | 1 |
2 | 5.265 | 1.66108 | 3.32216 | 4 |
3 | 3.846 | 1.34703 | 4.04109 | 9 |
4 | 2.809 | 1.03283 | 4.13132 | 16 |
5 | 2.052 | 0.71881 | 3.59405 | 25 |
6 | 1.499 | 0.40480 | 2.4288 | 36 |
Sum = 21 |
| 7.13988 | 19.49275 | 91 |
Normal equations are-
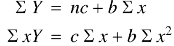
Putting the values form the table, we get-
7.13988 = 6c + 21b
19.49275 = 21c + 91b
On solving, we get-
b = -0.3141 and c = 2.28933
c = 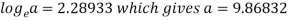
Now put these values in equations (1), we get-
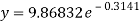
Q7) Estimate the chlorine residual in a swimming pool 5 hours after it has been treated with chemicals by fitting an exponential curve of the form
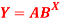 of the data given below-
of the data given below-
Hours(X) | 2 | 4 | 6 | 8 | 10 | 12 |
Chlorine residuals (Y) | 1.8 | 1.5 | 1.4 | 1.1 | 1.1 | 0.9 |
A7)
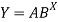
Taking log on the curve which is non-linear,
We get-
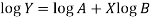
Put
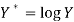
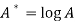
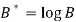
Then-
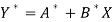
Which is the linear equation in X,
Its nomal equations are-
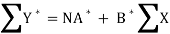
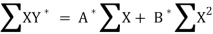
X Y Y* = ln Y X2 XY*
2 1.8 0.5878 4 0.1756
4 1.5 0.4055 16 1.622
6 1.4 0.3365 36 2.019
8 1.1 0.0953 64 0.7264
10 1.1 0.0953 100 0.953
12 0.9 -0.10536 144 -1.26432
42 1.415 364 5.26752
Here N = 6,
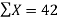
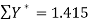
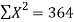
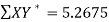
Thus the normal equations are-
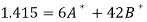
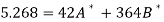
On solving, we get
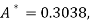
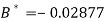
Or
A = 2.013 and B = 0.936
Hence the required least square exponential curve-
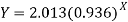
Prediction-
Chlorine content after 5 hours-
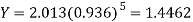
Q8) What do you understand by correlation?
A8)
When two variables are related in such a way that change in the value of one variable affects the value of the other variable, then these two variables are said to be correlated and there is correlation between two variables.
Example- Height and weight of the persons of a group.
The correlation is said to be perfect correlation if two variables vary in such a way that their ratio is constant always.
Scatter diagram-
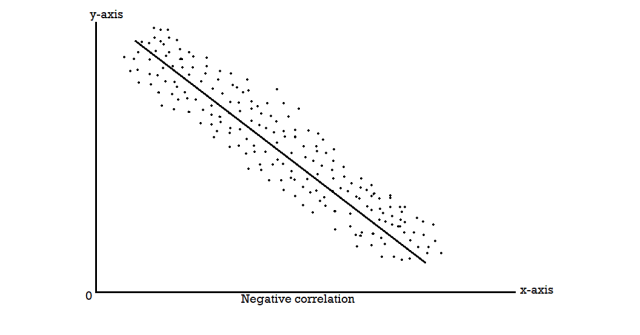
Correlation coefficient | Type of correlation |
+1 | Perfect positive correlation |
-1 | Perfect negative correlation |
0.25 | Weak positive correlation |
0.75 | Strong positive correlation |
-0.25 | Weak negative correlation |
-0.75 | Strong negative correlation |
0 | No correlation |
Q9) What is Karl Pearson’s coefficient of correlation?
A9)
Karl Pearson’s coefficient of correlation-
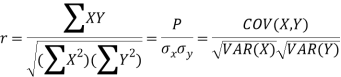
Here- 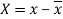 and
and 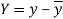
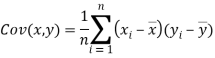
Note-
1. Correlation coefficient always lies between -1 and +1.
2. Correlation coefficient is independent of change of origin and scale.
3. If the two variables are independent then correlation coefficient between them is zero.
Q10) Find the correlation coefficient between Age and weight of the following data-
Age | 30 | 44 | 45 | 43 | 34 | 44 |
Weight | 56 | 55 | 60 | 64 | 62 | 63 |
A10)
x | y | 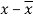 | 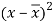 | 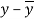 | 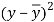 | ( 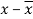 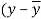 |
30 | 56 | -10 | 100 | -4 | 16 | 40 |
44 | 55 | 4 | 16 | -5 | 25 | -20 |
45 | 60 | 5 | 25 | 0 | 0 | 0 |
43 | 64 | 3 | 9 | 4 | 16 | 12 |
34 | 62 | -6 | 36 | 2 | 4 | -12 |
44 | 63 | 4 | 16 | 3 | 9 | 12 |
Sum= 240 |
360 |
0 |
202 |
0 |
70
|
32 |
Karl Pearson’s coefficient of correlation-
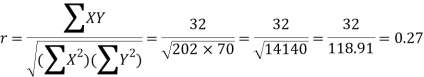
Here the correlation coefficient is 0.27.which is the positive correlation (weak positive correlation), this indicates that the as age increases, the weight also increase.
Q11) Ten students got the following percentage of marks in Economics and Statistics
Calculate the  of correlation.
of correlation.
Roll No. |  |  |  |  |  |  |  |  |  |  |
Marks in Economics |  |  |  |  |  |  |  |  |  |  |
Marks in  |  |  |  |  |  |  |  |  |  |  |
A11)
Let the marks of two subjects be denoted by 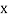 and
and 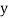 respectively.
respectively.
Then the mean for 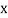 marks
marks 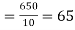 and the mean ofy marks
and the mean ofy marks 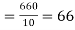
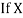 and
and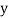 are deviations ofx’s and
are deviations ofx’s and 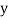 ’s from their respective means, then the data may be arranged in the following form:
’s from their respective means, then the data may be arranged in the following form:
x | y | X = x - 65 | Y = y - 66 | X2 | Y2 | X.Y |
78 36 98 25 75 82 90 62 65 39 650 | 84 51 91 60 68 62 86 58 53 47 660 | 13 -29 33 -40 10 17 25 -3 0 -26 0 | 18 -15 25 -6 2 -4 20 -8 -13 -19 0 | 169 841 1089 1600 100 289 625 9 0 676 5398
| 324 225 625 36 4 16 400 64 169 361 2224 | 234 435 825 240 20 -68 500 24 0 494 2704
|
|
|
|
| 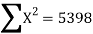 | 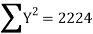 | 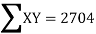 |
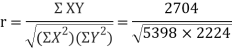
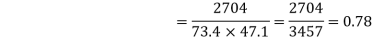
Q12) Find the correlation coefficient between the values X and Y of the dataset given below by using short-cut method-
X | 10 | 20 | 30 | 40 | 50 |
Y | 90 | 85 | 80 | 60 | 45 |
A12)
X | Y | 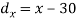 | 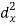 | 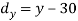 | 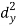 | 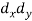 |
10 | 90 | -20 | 400 | 20 | 400 | -400 |
20 | 85 | -10 | 100 | 15 | 225 | -150 |
30 | 80 | 0 | 0 | 10 | 100 | 0 |
40 | 60 | 10 | 100 | -10 | 100 | -100 |
50 | 45 | 20 | 400 | -25 | 625 | -500 |
Sum = 150 |
360 |
0 |
1000 |
10 |
1450 |
-1150 |
Short-cut method to calculate correlation coefficient-
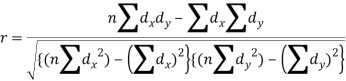
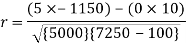
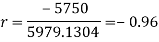
Q13) What is Spearman’s rank correlation?
A13)
Spearman’s rank correlation-
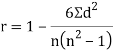
Solution. Let 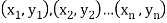 be the ranks of
be the ranks of 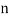 individuals corresponding to two characteristics.
individuals corresponding to two characteristics.
Assuming nor two individuals are equal in either classification, each individual takes the values 1, 2, 3, 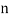 and hence their arithmetic means are, each
and hence their arithmetic means are, each
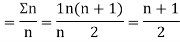
Let 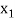 ,
, 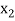 ,
, 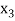 ,
, 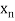 be the values of variable
be the values of variable 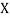 and
and 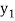 ,
, 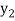 ,
, 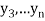 those of
those of 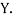
Then 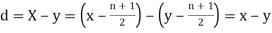
Where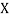 and y are deviations from the mean.
and y are deviations from the mean.
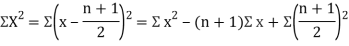
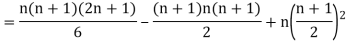
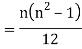
Clearly, 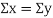 and
and 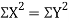
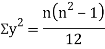
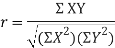
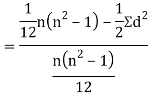
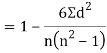
Q14) If X and Y are uncorrelated random variables,  the
the  of correlation between
of correlation between  and
and 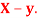
A14)
Let 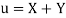 and
and 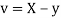
Then 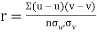
Now 
Similarly 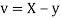
Now 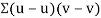
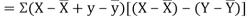
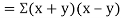
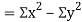
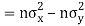
Also 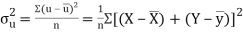
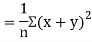
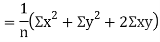
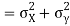 (As
(As 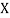 and
and 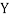 are not correlated, we have
are not correlated, we have 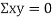 )
)
Similarly 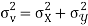
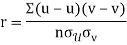
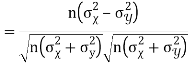
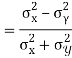
Q15) What do you understand by regression analysis?
A15)
If the scatter diagram indicates some relationship between two variables 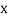 and
and 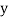 , then the dots of the scatter diagram will be concentrated round a curve. This curve is called the curve of regression. Regression analysis is the method used for estimating the unknown values of one variable corresponding to the known value of another variable.
, then the dots of the scatter diagram will be concentrated round a curve. This curve is called the curve of regression. Regression analysis is the method used for estimating the unknown values of one variable corresponding to the known value of another variable.
Or in other words, Regression is the measure of average relationship between independent and dependent variable
Regression can be used for two or more than two variables.
There are two types of variables in regression analysis.
1. Independent variable
2. Dependent variable
The variable which is used for prediction is called independent variable.
It is known as predictor or regressor.
The variable whose value is predicted by independent variable is called dependent variable or regressed or explained variable.
The scatter diagram shows relationship between independent and dependent variable, then the scatter diagram will be more or less concentrated round a curve, which is called the curve of regression.
When we find the curve as a straight line then it is known as line of regression and the regression is called linear regression.
Note- regression line is the best fit line which expresses the average relation between variables.
Q16) Two variables X and Y are given in the dataset below, find the two lines of regression.
x | 65 | 66 | 67 | 67 | 68 | 69 | 70 | 71 |
y | 66 | 68 | 65 | 69 | 74 | 73 | 72 | 70 |
A16)
The two lines of regression can be expressed as-
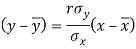
And
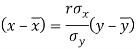
x | y | 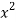 | 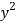 | Xy |
65 | 66 | 4225 | 4356 | 4290 |
66 | 68 | 4356 | 4624 | 4488 |
67 | 65 | 4489 | 4225 | 4355 |
67 | 69 | 4489 | 4761 | 4623 |
68 | 74 | 4624 | 5476 | 5032 |
69 | 73 | 4761 | 5329 | 5037 |
70 | 72 | 4900 | 5184 | 5040 |
71 | 70 | 5041 | 4900 | 4970 |
Sum = 543 | 557 | 36885 | 38855 | 37835 |
Now-
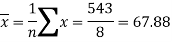
And
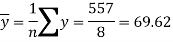
Standard deviation of x-
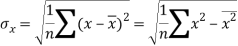

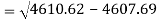
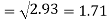
Similarly-
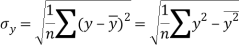
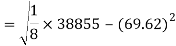
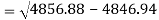
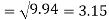
Correlation coefficient-
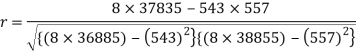
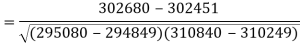
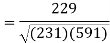
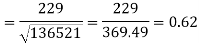
Put these values in regression line equation, we get
Regression line y on x-
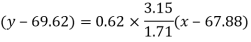
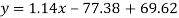
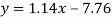
Regression line x on y-
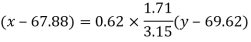
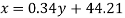
Unit – 5
Statistics
Q1) Find the straight line that best fits of the following data by using method of least square.
X | 1 | 2 | 3 | 4 | 5 |
y | 14 | 27 | 40 | 55 | 68 |
A1)
Suppose the straight line
y = a + bx…….. (1)
Fits the best-
Then-
x | y | Xy | 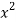 |
1 | 14 | 14 | 1 |
2 | 27 | 54 | 4 |
3 | 40 | 120 | 9 |
4 | 55 | 220 | 16 |
5 | 68 | 340 | 25 |
Sum = 15 | 204 | 748 | 55 |
Normal equations are-
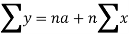
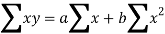
Put the values from the table, we get two normal equations-
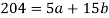
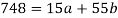
On solving the above equations, we get-
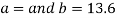
So that the best fit line will be- (on putting the values of a and b in equation (1))
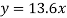
Q2) Find the best values of a and b so that y = a + bx fits the data given in the table
X | 0 | 1 | 2 | 3 | 4 |
Y | 1.0 | 2.9 | 4.8 | 6.7 | 8.6 |
A2)
y = a + bx
x | y | Xy | 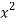 |
0 | 1.0 | 0 | 0 |
1 | 2.9 | 2.0 | 1 |
2 | 4.8 | 9.6 | 4 |
3 | 6.7 | 20.1 | 9 |
4 | 8.6 | 13.4 | 16 |
 | 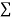 | 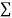 | 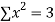 |
Normal equations, 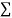 y= na+ b
y= na+ b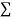 x (2)
x (2)
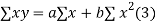
On putting the values of 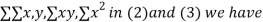
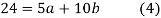
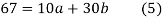
On solving (4) and (5) we get,
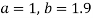
On substituting the values of a and b in (1) we get
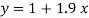
Q3) Fit a second degree parabola to the following data by least squares method.
 | 1929 | 1930 | 1931 | 1932 | 1933 | 1934 | 1935 | 1936 | 1937 |
 | 352 | 356 | 357 | 358 | 360 | 361 | 361 | 360 | 359 |
A3)
Taking x0 = 1933, y0 = 357
Taking u = x – x0, v = y – y0
u = x – 1933, v = y – 357
The equation y = a+bx+cx2 is transformed to v = A + Bu + Cu2 …(2)
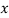 | u = x – 1933 | 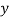 |  | 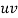 | 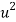 | u2v | u3 | u4 |
1929 | -4 | 352 | -5 | 20 | 16 | -80 | -64 | 256 |
1930 | -3 | 360 | -1 | 3 | 9 | -9 | -27 | 81 |
1931 | -2 | 357 | 0 | 0 | 4 | 0 | -8 | 16 |
1932 | -1 | 358 | 1 | -1 | 1 | 1 | -1 | 1 |
1933 | 0 | 360 | 3 | 0 | 0 | 0 | 0 | 0 |
1934 | 1 | 361 | 4 | 4 | 1 | 4 | 1 | 1 |
1935 | 2 | 361 | 4 | 8 | 4 | 16 | 8 | 16 |
1936 | 3 | 360 | 3 | 9 | 9 | 27 | 27 | 81 |
1937 | 4 | 359 | 2 | 8 | 16 | 32 | 64 | 256 |
Total | 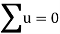 |
| 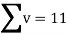 | 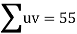 | 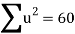 | 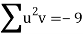 | 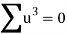 | 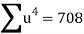 |
Normal equations are
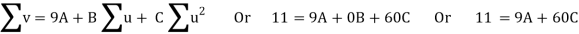

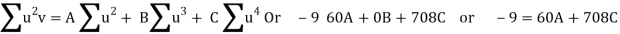
On solving these equations, we get A = 694/231, B = 17/20, C = - 247/924
V = 694/231 + 17/20 u – 247/924 u2V = 694/231 + 17/20 u – 247/924 u2
y – 357 = 694/231 + 17/20 (x – 1933) – 247/924 (x – 1933)2
= 694/231 + 17x/20 - 32861/20 – 247x2/924 (-3866x) – 247/924 + (1933)2
y = 694/231 – 32861/20 – 247/924 (1933)2 + 17x/20 + (247 3866)x/924 - 247 x2/924
y = 3 – 1643.05 – 998823.36 + 357 + 0.85 x + 1033.44 x – 0.267 x2
y = - 1000106.41 + 1034.29x – 0.267 x2
Q4) Find the least squares approximation of second degree for the discrete data
x | 2 | -1 | 0 | 1 | 2 |
y | 15 | 1 | 1 | 3 | 19 |
A4)
Let the equation of second degree polynomial be 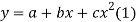
x | y | Xy | 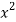 | 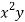 | 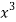 | 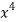 |
-2 | 15 | -30 | 4 | 60 | -8 | 16 |
-1 | 1 | -1 | 1 | 1 | -1 | 1 |
0 | 1 | 0 | 0 | 0 | 0 | 0 |
1 | 3 | 3 | 1 | 3 | 1 | 1 |
2 | 19 | 38 | 4 | 76 | 8 | 16 |
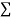 | 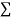 | 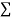 | 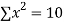 | 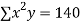 | 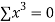 | 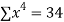 |
Normal equations are 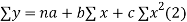
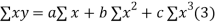
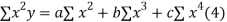
On putting the values of 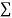 x,
x, 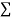 y,
y,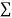 xy,
xy, 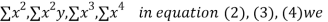 have
have
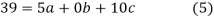
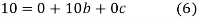
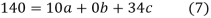
On solving (5),(6),(7), we get, 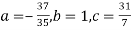
The required polynomial of second degree is
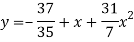
Q5) Fit a second degree parabola to the following data.
X = 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
Y = 1.1 | 1.3 | 1.6 | 2.0 | 2.7 | 3.4 | 4.1 |
A5)
We shift the origin to (2.5, 0) antique 0.5 as the new unit. This amounts to changing the variable x to X, by the relation X = 2x – 5.
Let the parabola of fit be y = a + bX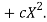 The values of
The values of  X etc. Are calculated as below:
X etc. Are calculated as below:
x | X | y | Xy |  | 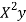 | 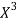 | 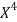 |
1.0 | -3 | 1.1 | -3.3 | 9 | 9.9 | -27 | 81 |
1.5 | -2 | 1.3 | -2.6 | 4 | 5.2 | -5 | 16 |
2.0 | -1 | 1.6 | -1.6 | 1 | 1.6 | -1 | 1 |
2.5 | 0 | 2.0 | 0.0 | 0 | 0.0 | 0 | 0 |
3.0 | 1 | 2.7 | 2.7 | 1 | 2.7 | 1 | 1 |
3.5 | 2 | 3.4 | 6.8 | 4 | 13.6 | 8 | 16 |
4.0 | 3 | 4.1 | 12.3 | 9 | 36.9 | 27 | 81 |
Total | 0 | 16.2 | 14.3 | 28 | 69.9 | 0 | 196 |
The normal equations are
7a + 28c =16.2; 28b =14.3;. 28a +196c=69.9
Solving these as simultaneous equations we get
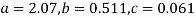
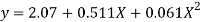
Replacing X bye 2x – 5 in the above equation we get
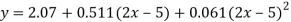
Which simplifies to y =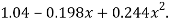
This is the required parabola of the best fit.
Q6) Fit the curve 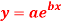 by using the method of least square.
by using the method of least square.
X | 1 | 2 | 3 | 4 | 5 | 6 |
Y | 7.209 | 5.265 | 3.846 | 2.809 | 2.052 | 1.499 |
A6)
Here-
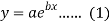
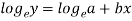
Now put-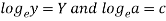
Then we get-
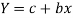
x | Y | 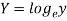 | XY | 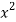 |
1 | 7.209 | 1.97533 | 1.97533 | 1 |
2 | 5.265 | 1.66108 | 3.32216 | 4 |
3 | 3.846 | 1.34703 | 4.04109 | 9 |
4 | 2.809 | 1.03283 | 4.13132 | 16 |
5 | 2.052 | 0.71881 | 3.59405 | 25 |
6 | 1.499 | 0.40480 | 2.4288 | 36 |
Sum = 21 |
| 7.13988 | 19.49275 | 91 |
Normal equations are-
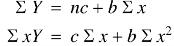
Putting the values form the table, we get-
7.13988 = 6c + 21b
19.49275 = 21c + 91b
On solving, we get-
b = -0.3141 and c = 2.28933
c = 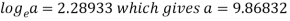
Now put these values in equations (1), we get-
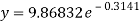
Q7) Estimate the chlorine residual in a swimming pool 5 hours after it has been treated with chemicals by fitting an exponential curve of the form
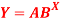 of the data given below-
of the data given below-
Hours(X) | 2 | 4 | 6 | 8 | 10 | 12 |
Chlorine residuals (Y) | 1.8 | 1.5 | 1.4 | 1.1 | 1.1 | 0.9 |
A7)
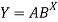
Taking log on the curve which is non-linear,
We get-
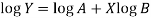
Put
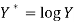
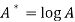
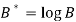
Then-
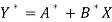
Which is the linear equation in X,
Its nomal equations are-
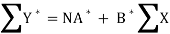
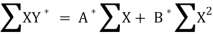
X Y Y* = ln Y X2 XY*
2 1.8 0.5878 4 0.1756
4 1.5 0.4055 16 1.622
6 1.4 0.3365 36 2.019
8 1.1 0.0953 64 0.7264
10 1.1 0.0953 100 0.953
12 0.9 -0.10536 144 -1.26432
42 1.415 364 5.26752
Here N = 6,
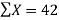
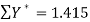
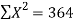
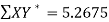
Thus the normal equations are-
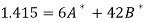
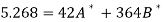
On solving, we get
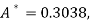
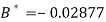
Or
A = 2.013 and B = 0.936
Hence the required least square exponential curve-
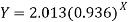
Prediction-
Chlorine content after 5 hours-
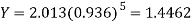
Q8) What do you understand by correlation?
A8)
When two variables are related in such a way that change in the value of one variable affects the value of the other variable, then these two variables are said to be correlated and there is correlation between two variables.
Example- Height and weight of the persons of a group.
The correlation is said to be perfect correlation if two variables vary in such a way that their ratio is constant always.
Scatter diagram-
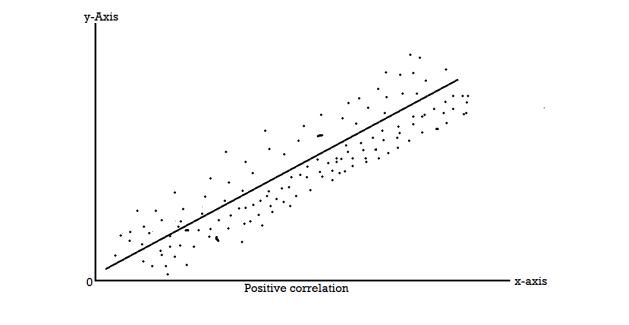
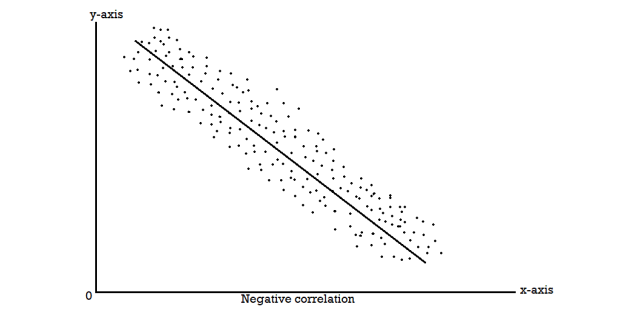
Correlation coefficient | Type of correlation |
+1 | Perfect positive correlation |
-1 | Perfect negative correlation |
0.25 | Weak positive correlation |
0.75 | Strong positive correlation |
-0.25 | Weak negative correlation |
-0.75 | Strong negative correlation |
0 | No correlation |
Q9) What is Karl Pearson’s coefficient of correlation?
A9)
Karl Pearson’s coefficient of correlation-
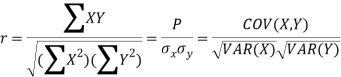
Here- 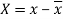 and
and 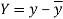
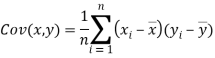
Note-
1. Correlation coefficient always lies between -1 and +1.
2. Correlation coefficient is independent of change of origin and scale.
3. If the two variables are independent then correlation coefficient between them is zero.
Q10) Find the correlation coefficient between Age and weight of the following data-
Age | 30 | 44 | 45 | 43 | 34 | 44 |
Weight | 56 | 55 | 60 | 64 | 62 | 63 |
A10)
x | y | 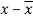 | 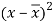 | 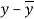 | 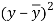 | ( 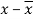 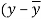 |
30 | 56 | -10 | 100 | -4 | 16 | 40 |
44 | 55 | 4 | 16 | -5 | 25 | -20 |
45 | 60 | 5 | 25 | 0 | 0 | 0 |
43 | 64 | 3 | 9 | 4 | 16 | 12 |
34 | 62 | -6 | 36 | 2 | 4 | -12 |
44 | 63 | 4 | 16 | 3 | 9 | 12 |
Sum= 240 |
360 |
0 |
202 |
0 |
70
|
32 |
Karl Pearson’s coefficient of correlation-
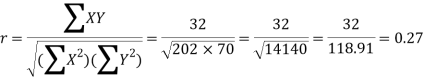
Here the correlation coefficient is 0.27.which is the positive correlation (weak positive correlation), this indicates that the as age increases, the weight also increase.
Q11) Ten students got the following percentage of marks in Economics and Statistics
Calculate the  of correlation.
of correlation.
Roll No. |  |  |  |  |  |  |  |  |  |  |
Marks in Economics |  |  |  |  |  |  |  |  |  |  |
Marks in  |  |  |  |  |  |  |  |  |  |  |
A11)
Let the marks of two subjects be denoted by 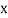 and
and 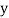 respectively.
respectively.
Then the mean for 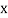 marks
marks 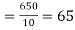 and the mean ofy marks
and the mean ofy marks 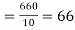
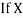 and
and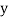 are deviations ofx’s and
are deviations ofx’s and 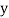 ’s from their respective means, then the data may be arranged in the following form:
’s from their respective means, then the data may be arranged in the following form:
x | y | X = x - 65 | Y = y - 66 | X2 | Y2 | X.Y |
78 36 98 25 75 82 90 62 65 39 650 | 84 51 91 60 68 62 86 58 53 47 660 | 13 -29 33 -40 10 17 25 -3 0 -26 0 | 18 -15 25 -6 2 -4 20 -8 -13 -19 0 | 169 841 1089 1600 100 289 625 9 0 676 5398
| 324 225 625 36 4 16 400 64 169 361 2224 | 234 435 825 240 20 -68 500 24 0 494 2704
|
|
|
|
| 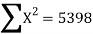 | 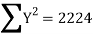 | 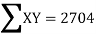 |
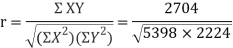
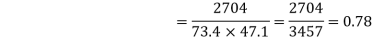
Q12) Find the correlation coefficient between the values X and Y of the dataset given below by using short-cut method-
X | 10 | 20 | 30 | 40 | 50 |
Y | 90 | 85 | 80 | 60 | 45 |
A12)
X | Y | 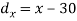 | 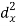 | 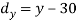 | 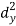 | 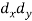 |
10 | 90 | -20 | 400 | 20 | 400 | -400 |
20 | 85 | -10 | 100 | 15 | 225 | -150 |
30 | 80 | 0 | 0 | 10 | 100 | 0 |
40 | 60 | 10 | 100 | -10 | 100 | -100 |
50 | 45 | 20 | 400 | -25 | 625 | -500 |
Sum = 150 |
360 |
0 |
1000 |
10 |
1450 |
-1150 |
Short-cut method to calculate correlation coefficient-
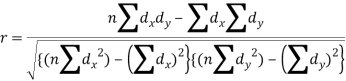
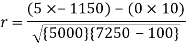
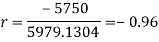
Q13) What is Spearman’s rank correlation?
A13)
Spearman’s rank correlation-
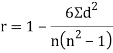
Solution. Let 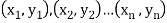 be the ranks of
be the ranks of 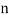 individuals corresponding to two characteristics.
individuals corresponding to two characteristics.
Assuming nor two individuals are equal in either classification, each individual takes the values 1, 2, 3, 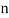 and hence their arithmetic means are, each
and hence their arithmetic means are, each
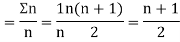
Let 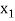 ,
, 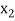 ,
, 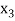 ,
, 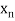 be the values of variable
be the values of variable 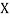 and
and 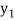 ,
, 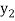 ,
, 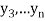 those of
those of 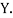
Then 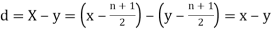
Where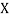 and y are deviations from the mean.
and y are deviations from the mean.
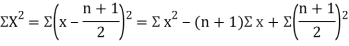
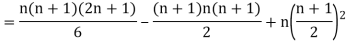
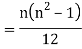
Clearly, 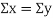 and
and 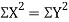
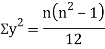
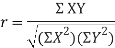
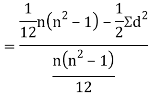
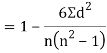
Q14) If X and Y are uncorrelated random variables,  the
the  of correlation between
of correlation between  and
and 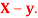
A14)
Let 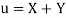 and
and 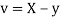
Then 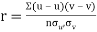
Now 
Similarly 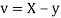
Now 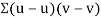
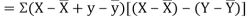
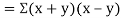
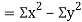
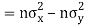
Also 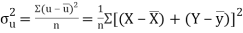
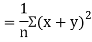
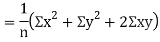
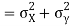 (As
(As 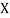 and
and 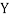 are not correlated, we have
are not correlated, we have 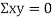 )
)
Similarly 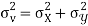
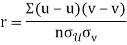
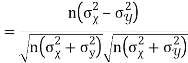
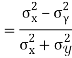
Q15) What do you understand by regression analysis?
A15)
If the scatter diagram indicates some relationship between two variables 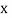 and
and 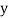 , then the dots of the scatter diagram will be concentrated round a curve. This curve is called the curve of regression. Regression analysis is the method used for estimating the unknown values of one variable corresponding to the known value of another variable.
, then the dots of the scatter diagram will be concentrated round a curve. This curve is called the curve of regression. Regression analysis is the method used for estimating the unknown values of one variable corresponding to the known value of another variable.
Or in other words, Regression is the measure of average relationship between independent and dependent variable
Regression can be used for two or more than two variables.
There are two types of variables in regression analysis.
1. Independent variable
2. Dependent variable
The variable which is used for prediction is called independent variable.
It is known as predictor or regressor.
The variable whose value is predicted by independent variable is called dependent variable or regressed or explained variable.
The scatter diagram shows relationship between independent and dependent variable, then the scatter diagram will be more or less concentrated round a curve, which is called the curve of regression.
When we find the curve as a straight line then it is known as line of regression and the regression is called linear regression.
Note- regression line is the best fit line which expresses the average relation between variables.
Q16) Two variables X and Y are given in the dataset below, find the two lines of regression.
x | 65 | 66 | 67 | 67 | 68 | 69 | 70 | 71 |
y | 66 | 68 | 65 | 69 | 74 | 73 | 72 | 70 |
A16)
The two lines of regression can be expressed as-
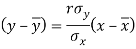
And
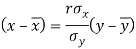
x | y | 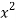 | 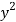 | Xy |
65 | 66 | 4225 | 4356 | 4290 |
66 | 68 | 4356 | 4624 | 4488 |
67 | 65 | 4489 | 4225 | 4355 |
67 | 69 | 4489 | 4761 | 4623 |
68 | 74 | 4624 | 5476 | 5032 |
69 | 73 | 4761 | 5329 | 5037 |
70 | 72 | 4900 | 5184 | 5040 |
71 | 70 | 5041 | 4900 | 4970 |
Sum = 543 | 557 | 36885 | 38855 | 37835 |
Now-
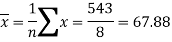
And
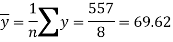
Standard deviation of x-
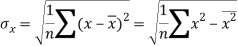

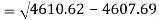
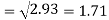
Similarly-
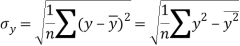
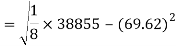
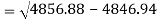
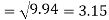
Correlation coefficient-
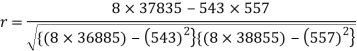
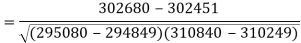
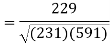
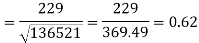
Put these values in regression line equation, we get
Regression line y on x-
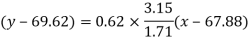
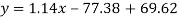
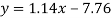
Regression line x on y-
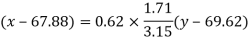
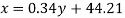
Unit – 5
Statistics
Q1) Find the straight line that best fits of the following data by using method of least square.
X | 1 | 2 | 3 | 4 | 5 |
y | 14 | 27 | 40 | 55 | 68 |
A1)
Suppose the straight line
y = a + bx…….. (1)
Fits the best-
Then-
x | y | Xy | 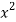 |
1 | 14 | 14 | 1 |
2 | 27 | 54 | 4 |
3 | 40 | 120 | 9 |
4 | 55 | 220 | 16 |
5 | 68 | 340 | 25 |
Sum = 15 | 204 | 748 | 55 |
Normal equations are-
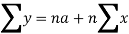
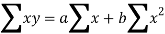
Put the values from the table, we get two normal equations-
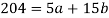
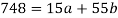
On solving the above equations, we get-
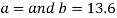
So that the best fit line will be- (on putting the values of a and b in equation (1))
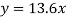
Q2) Find the best values of a and b so that y = a + bx fits the data given in the table
X | 0 | 1 | 2 | 3 | 4 |
Y | 1.0 | 2.9 | 4.8 | 6.7 | 8.6 |
A2)
y = a + bx
x | y | Xy | 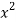 |
0 | 1.0 | 0 | 0 |
1 | 2.9 | 2.0 | 1 |
2 | 4.8 | 9.6 | 4 |
3 | 6.7 | 20.1 | 9 |
4 | 8.6 | 13.4 | 16 |
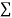 | 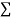 | 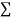 | 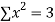 |
Normal equations, 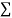 y= na+ b
y= na+ b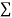 x (2)
x (2)
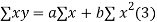
On putting the values of 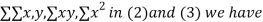
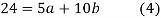
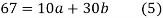
On solving (4) and (5) we get,
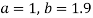
On substituting the values of a and b in (1) we get
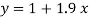
Q3) Fit a second degree parabola to the following data by least squares method.
 | 1929 | 1930 | 1931 | 1932 | 1933 | 1934 | 1935 | 1936 | 1937 |
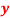 | 352 | 356 | 357 | 358 | 360 | 361 | 361 | 360 | 359 |
A3)
Taking x0 = 1933, y0 = 357
Taking u = x – x0, v = y – y0
u = x – 1933, v = y – 357
The equation y = a+bx+cx2 is transformed to v = A + Bu + Cu2 …(2)
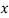 | u = x – 1933 | 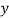 |  | 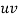 | 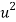 | u2v | u3 | u4 |
1929 | -4 | 352 | -5 | 20 | 16 | -80 | -64 | 256 |
1930 | -3 | 360 | -1 | 3 | 9 | -9 | -27 | 81 |
1931 | -2 | 357 | 0 | 0 | 4 | 0 | -8 | 16 |
1932 | -1 | 358 | 1 | -1 | 1 | 1 | -1 | 1 |
1933 | 0 | 360 | 3 | 0 | 0 | 0 | 0 | 0 |
1934 | 1 | 361 | 4 | 4 | 1 | 4 | 1 | 1 |
1935 | 2 | 361 | 4 | 8 | 4 | 16 | 8 | 16 |
1936 | 3 | 360 | 3 | 9 | 9 | 27 | 27 | 81 |
1937 | 4 | 359 | 2 | 8 | 16 | 32 | 64 | 256 |
Total | 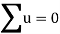 |
| 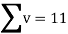 | 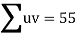 | 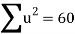 | 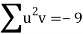 | 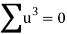 | 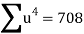 |
Normal equations are
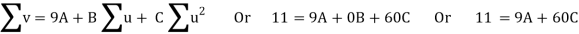

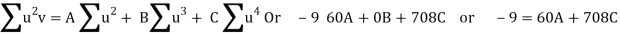
On solving these equations, we get A = 694/231, B = 17/20, C = - 247/924
V = 694/231 + 17/20 u – 247/924 u2V = 694/231 + 17/20 u – 247/924 u2
y – 357 = 694/231 + 17/20 (x – 1933) – 247/924 (x – 1933)2
= 694/231 + 17x/20 - 32861/20 – 247x2/924 (-3866x) – 247/924 + (1933)2
y = 694/231 – 32861/20 – 247/924 (1933)2 + 17x/20 + (247 3866)x/924 - 247 x2/924
y = 3 – 1643.05 – 998823.36 + 357 + 0.85 x + 1033.44 x – 0.267 x2
y = - 1000106.41 + 1034.29x – 0.267 x2
Q4) Find the least squares approximation of second degree for the discrete data
x | 2 | -1 | 0 | 1 | 2 |
y | 15 | 1 | 1 | 3 | 19 |
A4)
Let the equation of second degree polynomial be 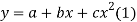
x | y | Xy | 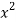 | 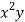 | 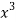 | 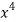 |
-2 | 15 | -30 | 4 | 60 | -8 | 16 |
-1 | 1 | -1 | 1 | 1 | -1 | 1 |
0 | 1 | 0 | 0 | 0 | 0 | 0 |
1 | 3 | 3 | 1 | 3 | 1 | 1 |
2 | 19 | 38 | 4 | 76 | 8 | 16 |
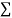 |  |  | 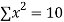 | 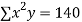 | 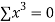 | 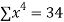 |
Normal equations are 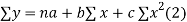
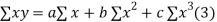
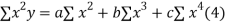
On putting the values of 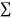 x,
x, 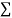 y,
y,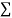 xy,
xy, 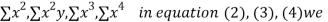 have
have
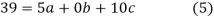
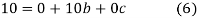
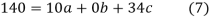
On solving (5),(6),(7), we get, 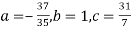
The required polynomial of second degree is
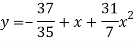
Q5) Fit a second degree parabola to the following data.
X = 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
Y = 1.1 | 1.3 | 1.6 | 2.0 | 2.7 | 3.4 | 4.1 |
A5)
We shift the origin to (2.5, 0) antique 0.5 as the new unit. This amounts to changing the variable x to X, by the relation X = 2x – 5.
Let the parabola of fit be y = a + bX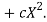 The values of
The values of  X etc. Are calculated as below:
X etc. Are calculated as below:
x | X | y | Xy | 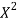 | 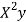 | 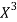 | 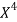 |
1.0 | -3 | 1.1 | -3.3 | 9 | 9.9 | -27 | 81 |
1.5 | -2 | 1.3 | -2.6 | 4 | 5.2 | -5 | 16 |
2.0 | -1 | 1.6 | -1.6 | 1 | 1.6 | -1 | 1 |
2.5 | 0 | 2.0 | 0.0 | 0 | 0.0 | 0 | 0 |
3.0 | 1 | 2.7 | 2.7 | 1 | 2.7 | 1 | 1 |
3.5 | 2 | 3.4 | 6.8 | 4 | 13.6 | 8 | 16 |
4.0 | 3 | 4.1 | 12.3 | 9 | 36.9 | 27 | 81 |
Total | 0 | 16.2 | 14.3 | 28 | 69.9 | 0 | 196 |
The normal equations are
7a + 28c =16.2; 28b =14.3;. 28a +196c=69.9
Solving these as simultaneous equations we get
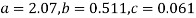
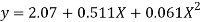
Replacing X bye 2x – 5 in the above equation we get
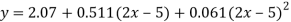
Which simplifies to y =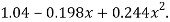
This is the required parabola of the best fit.
Q6) Fit the curve 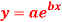 by using the method of least square.
by using the method of least square.
X | 1 | 2 | 3 | 4 | 5 | 6 |
Y | 7.209 | 5.265 | 3.846 | 2.809 | 2.052 | 1.499 |
A6)
Here-
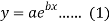
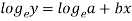
Now put-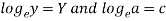
Then we get-
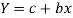
x | Y | 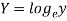 | XY | 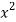 |
1 | 7.209 | 1.97533 | 1.97533 | 1 |
2 | 5.265 | 1.66108 | 3.32216 | 4 |
3 | 3.846 | 1.34703 | 4.04109 | 9 |
4 | 2.809 | 1.03283 | 4.13132 | 16 |
5 | 2.052 | 0.71881 | 3.59405 | 25 |
6 | 1.499 | 0.40480 | 2.4288 | 36 |
Sum = 21 |
| 7.13988 | 19.49275 | 91 |
Normal equations are-
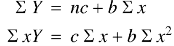
Putting the values form the table, we get-
7.13988 = 6c + 21b
19.49275 = 21c + 91b
On solving, we get-
b = -0.3141 and c = 2.28933
c = 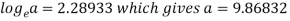
Now put these values in equations (1), we get-
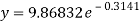
Q7) Estimate the chlorine residual in a swimming pool 5 hours after it has been treated with chemicals by fitting an exponential curve of the form
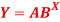 of the data given below-
of the data given below-
Hours(X) | 2 | 4 | 6 | 8 | 10 | 12 |
Chlorine residuals (Y) | 1.8 | 1.5 | 1.4 | 1.1 | 1.1 | 0.9 |
A7)
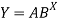
Taking log on the curve which is non-linear,
We get-
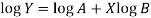
Put
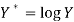
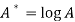
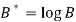
Then-
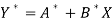
Which is the linear equation in X,
Its nomal equations are-
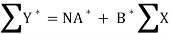
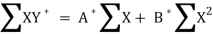
X Y Y* = ln Y X2 XY*
2 1.8 0.5878 4 0.1756
4 1.5 0.4055 16 1.622
6 1.4 0.3365 36 2.019
8 1.1 0.0953 64 0.7264
10 1.1 0.0953 100 0.953
12 0.9 -0.10536 144 -1.26432
42 1.415 364 5.26752
Here N = 6,
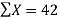
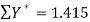
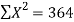
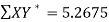
Thus the normal equations are-
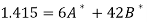
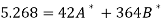
On solving, we get
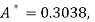
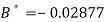
Or
A = 2.013 and B = 0.936
Hence the required least square exponential curve-
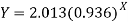
Prediction-
Chlorine content after 5 hours-
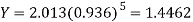
Q8) What do you understand by correlation?
A8)
When two variables are related in such a way that change in the value of one variable affects the value of the other variable, then these two variables are said to be correlated and there is correlation between two variables.
Example- Height and weight of the persons of a group.
The correlation is said to be perfect correlation if two variables vary in such a way that their ratio is constant always.
Scatter diagram-
Correlation coefficient | Type of correlation |
+1 | Perfect positive correlation |
-1 | Perfect negative correlation |
0.25 | Weak positive correlation |
0.75 | Strong positive correlation |
-0.25 | Weak negative correlation |
-0.75 | Strong negative correlation |
0 | No correlation |
Q9) What is Karl Pearson’s coefficient of correlation?
A9)
Karl Pearson’s coefficient of correlation-
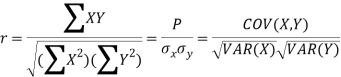
Here- 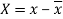 and
and 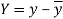
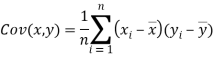
Note-
1. Correlation coefficient always lies between -1 and +1.
2. Correlation coefficient is independent of change of origin and scale.
3. If the two variables are independent then correlation coefficient between them is zero.
Q10) Find the correlation coefficient between Age and weight of the following data-
Age | 30 | 44 | 45 | 43 | 34 | 44 |
Weight | 56 | 55 | 60 | 64 | 62 | 63 |
A10)
x | y | 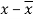 | 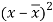 | 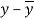 | 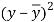 | ( 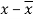 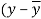 |
30 | 56 | -10 | 100 | -4 | 16 | 40 |
44 | 55 | 4 | 16 | -5 | 25 | -20 |
45 | 60 | 5 | 25 | 0 | 0 | 0 |
43 | 64 | 3 | 9 | 4 | 16 | 12 |
34 | 62 | -6 | 36 | 2 | 4 | -12 |
44 | 63 | 4 | 16 | 3 | 9 | 12 |
Sum= 240 |
360 |
0 |
202 |
0 |
70
|
32 |
Karl Pearson’s coefficient of correlation-
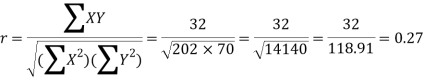
Here the correlation coefficient is 0.27.which is the positive correlation (weak positive correlation), this indicates that the as age increases, the weight also increase.
Q11) Ten students got the following percentage of marks in Economics and Statistics
Calculate the  of correlation.
of correlation.
Roll No. |  |  |  |  |  |  |  |  |  |  |
Marks in Economics |  |  |  |  |  |  |  |  |  |  |
Marks in  |  |  |  |  |  |  |  |  |  |  |
A11)
Let the marks of two subjects be denoted by 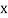 and
and 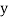 respectively.
respectively.
Then the mean for 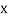 marks
marks 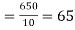 and the mean ofy marks
and the mean ofy marks 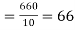
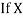 and
and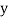 are deviations ofx’s and
are deviations ofx’s and 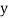 ’s from their respective means, then the data may be arranged in the following form:
’s from their respective means, then the data may be arranged in the following form:
x | y | X = x - 65 | Y = y - 66 | X2 | Y2 | X.Y |
78 36 98 25 75 82 90 62 65 39 650 | 84 51 91 60 68 62 86 58 53 47 660 | 13 -29 33 -40 10 17 25 -3 0 -26 0 | 18 -15 25 -6 2 -4 20 -8 -13 -19 0 | 169 841 1089 1600 100 289 625 9 0 676 5398
| 324 225 625 36 4 16 400 64 169 361 2224 | 234 435 825 240 20 -68 500 24 0 494 2704
|
|
|
|
| 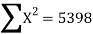 | 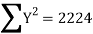 | 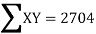 |
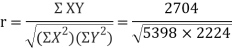
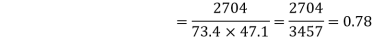
Q12) Find the correlation coefficient between the values X and Y of the dataset given below by using short-cut method-
X | 10 | 20 | 30 | 40 | 50 |
Y | 90 | 85 | 80 | 60 | 45 |
A12)
X | Y | 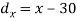 | 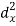 | 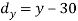 | 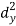 | 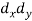 |
10 | 90 | -20 | 400 | 20 | 400 | -400 |
20 | 85 | -10 | 100 | 15 | 225 | -150 |
30 | 80 | 0 | 0 | 10 | 100 | 0 |
40 | 60 | 10 | 100 | -10 | 100 | -100 |
50 | 45 | 20 | 400 | -25 | 625 | -500 |
Sum = 150 |
360 |
0 |
1000 |
10 |
1450 |
-1150 |
Short-cut method to calculate correlation coefficient-
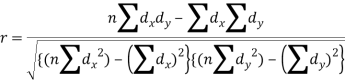
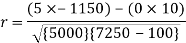
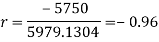
Q13) What is Spearman’s rank correlation?
A13)
Spearman’s rank correlation-
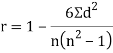
Solution. Let 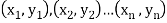 be the ranks of
be the ranks of 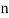 individuals corresponding to two characteristics.
individuals corresponding to two characteristics.
Assuming nor two individuals are equal in either classification, each individual takes the values 1, 2, 3, 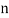 and hence their arithmetic means are, each
and hence their arithmetic means are, each
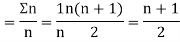
Let 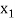 ,
, 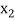 ,
, 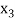 ,
, 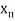 be the values of variable
be the values of variable 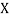 and
and 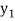 ,
, 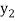 ,
, 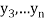 those of
those of 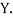
Then 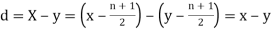
Where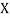 and y are deviations from the mean.
and y are deviations from the mean.
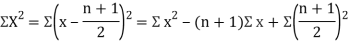
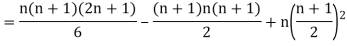
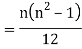
Clearly, 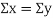 and
and 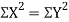
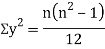
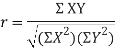
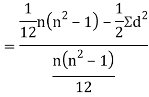
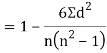
Q14) If X and Y are uncorrelated random variables,  the
the  of correlation between
of correlation between  and
and 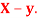
A14)
Let 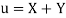 and
and 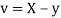
Then 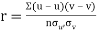
Now 
Similarly 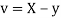
Now 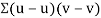
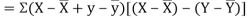
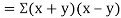
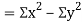
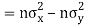
Also 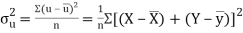
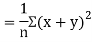
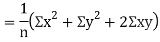
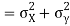 (As
(As 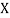 and
and 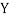 are not correlated, we have
are not correlated, we have 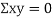 )
)
Similarly 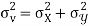
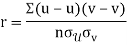
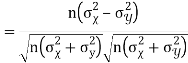
Q15) What do you understand by regression analysis?
A15)
If the scatter diagram indicates some relationship between two variables 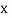 and
and 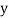 , then the dots of the scatter diagram will be concentrated round a curve. This curve is called the curve of regression. Regression analysis is the method used for estimating the unknown values of one variable corresponding to the known value of another variable.
, then the dots of the scatter diagram will be concentrated round a curve. This curve is called the curve of regression. Regression analysis is the method used for estimating the unknown values of one variable corresponding to the known value of another variable.
Or in other words, Regression is the measure of average relationship between independent and dependent variable
Regression can be used for two or more than two variables.
There are two types of variables in regression analysis.
1. Independent variable
2. Dependent variable
The variable which is used for prediction is called independent variable.
It is known as predictor or regressor.
The variable whose value is predicted by independent variable is called dependent variable or regressed or explained variable.
The scatter diagram shows relationship between independent and dependent variable, then the scatter diagram will be more or less concentrated round a curve, which is called the curve of regression.
When we find the curve as a straight line then it is known as line of regression and the regression is called linear regression.
Note- regression line is the best fit line which expresses the average relation between variables.
Q16) Two variables X and Y are given in the dataset below, find the two lines of regression.
x | 65 | 66 | 67 | 67 | 68 | 69 | 70 | 71 |
y | 66 | 68 | 65 | 69 | 74 | 73 | 72 | 70 |
A16)
The two lines of regression can be expressed as-
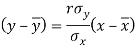
And
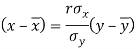
x | y | 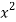 | 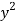 | Xy |
65 | 66 | 4225 | 4356 | 4290 |
66 | 68 | 4356 | 4624 | 4488 |
67 | 65 | 4489 | 4225 | 4355 |
67 | 69 | 4489 | 4761 | 4623 |
68 | 74 | 4624 | 5476 | 5032 |
69 | 73 | 4761 | 5329 | 5037 |
70 | 72 | 4900 | 5184 | 5040 |
71 | 70 | 5041 | 4900 | 4970 |
Sum = 543 | 557 | 36885 | 38855 | 37835 |
Now-
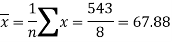
And
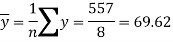
Standard deviation of x-
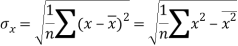

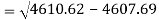
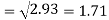
Similarly-
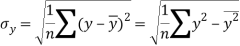
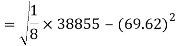
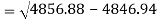
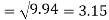
Correlation coefficient-
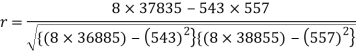
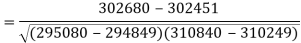
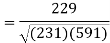
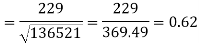
Put these values in regression line equation, we get
Regression line y on x-
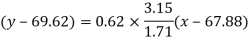
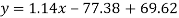
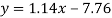
Regression line x on y-
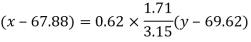
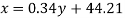
Unit – 5
Statistics
Q1) Find the straight line that best fits of the following data by using method of least square.
X | 1 | 2 | 3 | 4 | 5 |
y | 14 | 27 | 40 | 55 | 68 |
A1)
Suppose the straight line
y = a + bx…….. (1)
Fits the best-
Then-
x | y | Xy | 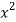 |
1 | 14 | 14 | 1 |
2 | 27 | 54 | 4 |
3 | 40 | 120 | 9 |
4 | 55 | 220 | 16 |
5 | 68 | 340 | 25 |
Sum = 15 | 204 | 748 | 55 |
Normal equations are-
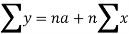
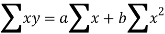
Put the values from the table, we get two normal equations-
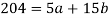
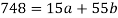
On solving the above equations, we get-
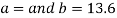
So that the best fit line will be- (on putting the values of a and b in equation (1))
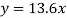
Q2) Find the best values of a and b so that y = a + bx fits the data given in the table
X | 0 | 1 | 2 | 3 | 4 |
Y | 1.0 | 2.9 | 4.8 | 6.7 | 8.6 |
A2)
y = a + bx
x | y | Xy | 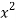 |
0 | 1.0 | 0 | 0 |
1 | 2.9 | 2.0 | 1 |
2 | 4.8 | 9.6 | 4 |
3 | 6.7 | 20.1 | 9 |
4 | 8.6 | 13.4 | 16 |
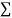 | 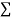 | 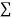 | 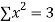 |
Normal equations, 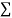 y= na+ b
y= na+ b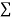 x (2)
x (2)
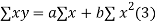
On putting the values of 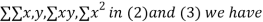
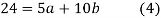
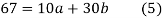
On solving (4) and (5) we get,
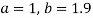
On substituting the values of a and b in (1) we get
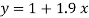
Q3) Fit a second degree parabola to the following data by least squares method.
 | 1929 | 1930 | 1931 | 1932 | 1933 | 1934 | 1935 | 1936 | 1937 |
 | 352 | 356 | 357 | 358 | 360 | 361 | 361 | 360 | 359 |
A3)
Taking x0 = 1933, y0 = 357
Taking u = x – x0, v = y – y0
u = x – 1933, v = y – 357
The equation y = a+bx+cx2 is transformed to v = A + Bu + Cu2 …(2)
 | u = x – 1933 |  |  | 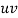 | 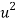 | u2v | u3 | u4 |
1929 | -4 | 352 | -5 | 20 | 16 | -80 | -64 | 256 |
1930 | -3 | 360 | -1 | 3 | 9 | -9 | -27 | 81 |
1931 | -2 | 357 | 0 | 0 | 4 | 0 | -8 | 16 |
1932 | -1 | 358 | 1 | -1 | 1 | 1 | -1 | 1 |
1933 | 0 | 360 | 3 | 0 | 0 | 0 | 0 | 0 |
1934 | 1 | 361 | 4 | 4 | 1 | 4 | 1 | 1 |
1935 | 2 | 361 | 4 | 8 | 4 | 16 | 8 | 16 |
1936 | 3 | 360 | 3 | 9 | 9 | 27 | 27 | 81 |
1937 | 4 | 359 | 2 | 8 | 16 | 32 | 64 | 256 |
Total | 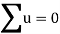 |
| 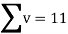 | 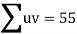 | 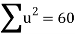 | 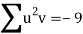 | 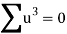 | 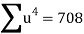 |
Normal equations are
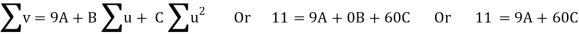

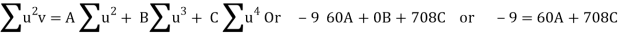
On solving these equations, we get A = 694/231, B = 17/20, C = - 247/924
V = 694/231 + 17/20 u – 247/924 u2V = 694/231 + 17/20 u – 247/924 u2
y – 357 = 694/231 + 17/20 (x – 1933) – 247/924 (x – 1933)2
= 694/231 + 17x/20 - 32861/20 – 247x2/924 (-3866x) – 247/924 + (1933)2
y = 694/231 – 32861/20 – 247/924 (1933)2 + 17x/20 + (247 3866)x/924 - 247 x2/924
y = 3 – 1643.05 – 998823.36 + 357 + 0.85 x + 1033.44 x – 0.267 x2
y = - 1000106.41 + 1034.29x – 0.267 x2
Q4) Find the least squares approximation of second degree for the discrete data
x | 2 | -1 | 0 | 1 | 2 |
y | 15 | 1 | 1 | 3 | 19 |
A4)
Let the equation of second degree polynomial be 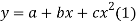
x | y | Xy | 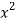 | 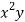 | 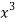 | 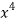 |
-2 | 15 | -30 | 4 | 60 | -8 | 16 |
-1 | 1 | -1 | 1 | 1 | -1 | 1 |
0 | 1 | 0 | 0 | 0 | 0 | 0 |
1 | 3 | 3 | 1 | 3 | 1 | 1 |
2 | 19 | 38 | 4 | 76 | 8 | 16 |
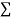 | 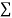 | 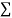 | 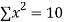 | 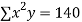 | 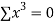 | 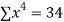 |
Normal equations are 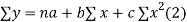
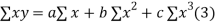
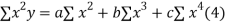
On putting the values of 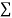 x,
x, 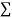 y,
y,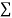 xy,
xy, 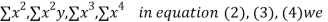 have
have
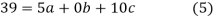
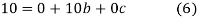
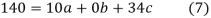
On solving (5),(6),(7), we get, 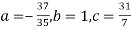
The required polynomial of second degree is
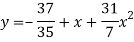
Q5) Fit a second degree parabola to the following data.
X = 1.0 | 1.5 | 2.0 | 2.5 | 3.0 | 3.5 | 4.0 |
Y = 1.1 | 1.3 | 1.6 | 2.0 | 2.7 | 3.4 | 4.1 |
A5)
We shift the origin to (2.5, 0) antique 0.5 as the new unit. This amounts to changing the variable x to X, by the relation X = 2x – 5.
Let the parabola of fit be y = a + bX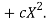 The values of
The values of 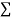 X etc. Are calculated as below:
X etc. Are calculated as below:
x | X | y | Xy | 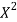 | 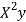 | 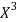 | 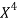 |
1.0 | -3 | 1.1 | -3.3 | 9 | 9.9 | -27 | 81 |
1.5 | -2 | 1.3 | -2.6 | 4 | 5.2 | -5 | 16 |
2.0 | -1 | 1.6 | -1.6 | 1 | 1.6 | -1 | 1 |
2.5 | 0 | 2.0 | 0.0 | 0 | 0.0 | 0 | 0 |
3.0 | 1 | 2.7 | 2.7 | 1 | 2.7 | 1 | 1 |
3.5 | 2 | 3.4 | 6.8 | 4 | 13.6 | 8 | 16 |
4.0 | 3 | 4.1 | 12.3 | 9 | 36.9 | 27 | 81 |
Total | 0 | 16.2 | 14.3 | 28 | 69.9 | 0 | 196 |
The normal equations are
7a + 28c =16.2; 28b =14.3;. 28a +196c=69.9
Solving these as simultaneous equations we get
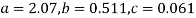
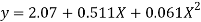
Replacing X bye 2x – 5 in the above equation we get
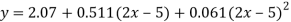
Which simplifies to y =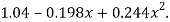
This is the required parabola of the best fit.
Q6) Fit the curve 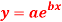 by using the method of least square.
by using the method of least square.
X | 1 | 2 | 3 | 4 | 5 | 6 |
Y | 7.209 | 5.265 | 3.846 | 2.809 | 2.052 | 1.499 |
A6)
Here-
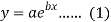
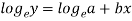
Now put-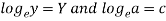
Then we get-
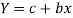
x | Y | 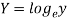 | XY | 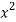 |
1 | 7.209 | 1.97533 | 1.97533 | 1 |
2 | 5.265 | 1.66108 | 3.32216 | 4 |
3 | 3.846 | 1.34703 | 4.04109 | 9 |
4 | 2.809 | 1.03283 | 4.13132 | 16 |
5 | 2.052 | 0.71881 | 3.59405 | 25 |
6 | 1.499 | 0.40480 | 2.4288 | 36 |
Sum = 21 |
| 7.13988 | 19.49275 | 91 |
Normal equations are-
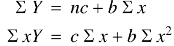
Putting the values form the table, we get-
7.13988 = 6c + 21b
19.49275 = 21c + 91b
On solving, we get-
b = -0.3141 and c = 2.28933
c = 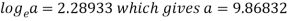
Now put these values in equations (1), we get-
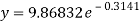
Q7) Estimate the chlorine residual in a swimming pool 5 hours after it has been treated with chemicals by fitting an exponential curve of the form
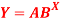 of the data given below-
of the data given below-
Hours(X) | 2 | 4 | 6 | 8 | 10 | 12 |
Chlorine residuals (Y) | 1.8 | 1.5 | 1.4 | 1.1 | 1.1 | 0.9 |
A7)
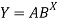
Taking log on the curve which is non-linear,
We get-
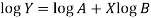
Put
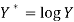
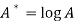
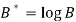
Then-
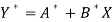
Which is the linear equation in X,
Its nomal equations are-
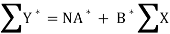
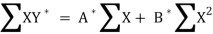
X Y Y* = ln Y X2 XY*
2 1.8 0.5878 4 0.1756
4 1.5 0.4055 16 1.622
6 1.4 0.3365 36 2.019
8 1.1 0.0953 64 0.7264
10 1.1 0.0953 100 0.953
12 0.9 -0.10536 144 -1.26432
42 1.415 364 5.26752
Here N = 6,
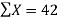
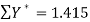
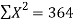
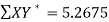
Thus the normal equations are-
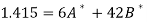
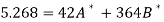
On solving, we get
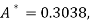
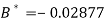
Or
A = 2.013 and B = 0.936
Hence the required least square exponential curve-
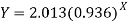
Prediction-
Chlorine content after 5 hours-
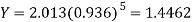
Q8) What do you understand by correlation?
A8)
When two variables are related in such a way that change in the value of one variable affects the value of the other variable, then these two variables are said to be correlated and there is correlation between two variables.
Example- Height and weight of the persons of a group.
The correlation is said to be perfect correlation if two variables vary in such a way that their ratio is constant always.
Scatter diagram-
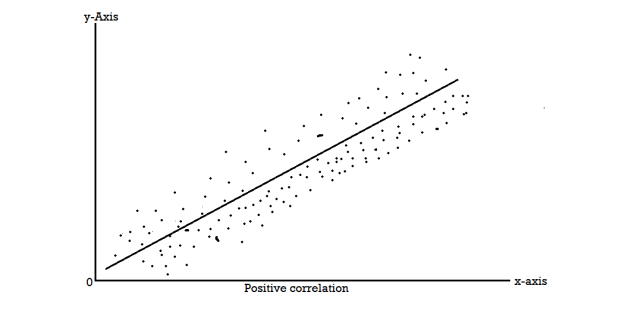
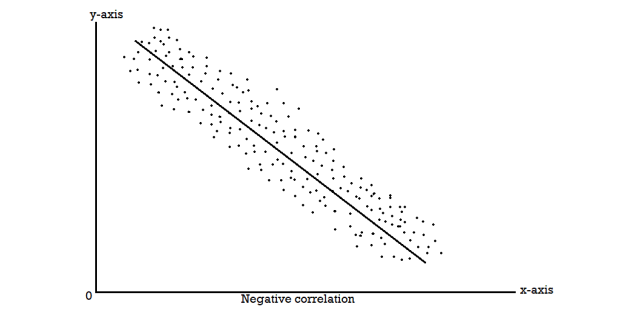
Correlation coefficient | Type of correlation |
+1 | Perfect positive correlation |
-1 | Perfect negative correlation |
0.25 | Weak positive correlation |
0.75 | Strong positive correlation |
-0.25 | Weak negative correlation |
-0.75 | Strong negative correlation |
0 | No correlation |
Q9) What is Karl Pearson’s coefficient of correlation?
A9)
Karl Pearson’s coefficient of correlation-
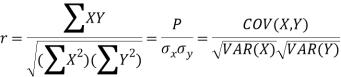
Here- 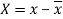 and
and 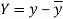
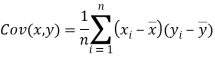
Note-
1. Correlation coefficient always lies between -1 and +1.
2. Correlation coefficient is independent of change of origin and scale.
3. If the two variables are independent then correlation coefficient between them is zero.
Q10) Find the correlation coefficient between Age and weight of the following data-
Age | 30 | 44 | 45 | 43 | 34 | 44 |
Weight | 56 | 55 | 60 | 64 | 62 | 63 |
A10)
x | y | 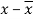 | 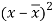 | 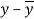 | 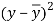 | ( 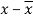 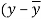 |
30 | 56 | -10 | 100 | -4 | 16 | 40 |
44 | 55 | 4 | 16 | -5 | 25 | -20 |
45 | 60 | 5 | 25 | 0 | 0 | 0 |
43 | 64 | 3 | 9 | 4 | 16 | 12 |
34 | 62 | -6 | 36 | 2 | 4 | -12 |
44 | 63 | 4 | 16 | 3 | 9 | 12 |
Sum= 240 |
360 |
0 |
202 |
0 |
70
|
32 |
Karl Pearson’s coefficient of correlation-
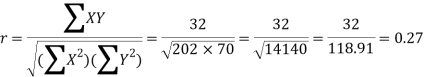
Here the correlation coefficient is 0.27.which is the positive correlation (weak positive correlation), this indicates that the as age increases, the weight also increase.
Q11) Ten students got the following percentage of marks in Economics and Statistics
Calculate the  of correlation.
of correlation.
Roll No. |  |  |  |  |  |  |  |  |  |  |
Marks in Economics |  |  |  |  |  |  |  |  |  |  |
Marks in  |  |  |  |  |  |  |  |  |  |  |
A11)
Let the marks of two subjects be denoted by 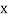 and
and 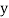 respectively.
respectively.
Then the mean for 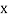 marks
marks 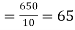 and the mean ofy marks
and the mean ofy marks 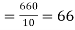
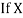 and
and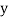 are deviations ofx’s and
are deviations ofx’s and 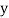 ’s from their respective means, then the data may be arranged in the following form:
’s from their respective means, then the data may be arranged in the following form:
x | y | X = x - 65 | Y = y - 66 | X2 | Y2 | X.Y |
78 36 98 25 75 82 90 62 65 39 650 | 84 51 91 60 68 62 86 58 53 47 660 | 13 -29 33 -40 10 17 25 -3 0 -26 0 | 18 -15 25 -6 2 -4 20 -8 -13 -19 0 | 169 841 1089 1600 100 289 625 9 0 676 5398
| 324 225 625 36 4 16 400 64 169 361 2224 | 234 435 825 240 20 -68 500 24 0 494 2704
|
|
|
|
| 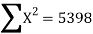 | 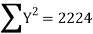 | 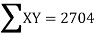 |
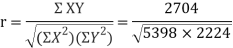
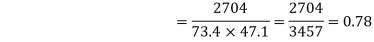
Q12) Find the correlation coefficient between the values X and Y of the dataset given below by using short-cut method-
X | 10 | 20 | 30 | 40 | 50 |
Y | 90 | 85 | 80 | 60 | 45 |
A12)
X | Y | 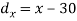 | 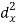 | 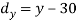 | 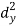 | 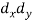 |
10 | 90 | -20 | 400 | 20 | 400 | -400 |
20 | 85 | -10 | 100 | 15 | 225 | -150 |
30 | 80 | 0 | 0 | 10 | 100 | 0 |
40 | 60 | 10 | 100 | -10 | 100 | -100 |
50 | 45 | 20 | 400 | -25 | 625 | -500 |
Sum = 150 |
360 |
0 |
1000 |
10 |
1450 |
-1150 |
Short-cut method to calculate correlation coefficient-
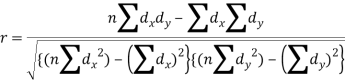
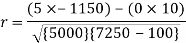
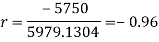
Q13) What is Spearman’s rank correlation?
A13)
Spearman’s rank correlation-
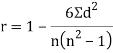
Solution. Let 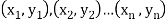 be the ranks of
be the ranks of 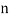 individuals corresponding to two characteristics.
individuals corresponding to two characteristics.
Assuming nor two individuals are equal in either classification, each individual takes the values 1, 2, 3, 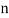 and hence their arithmetic means are, each
and hence their arithmetic means are, each
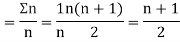
Let 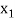 ,
, 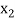 ,
, 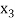 ,
, 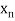 be the values of variable
be the values of variable 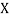 and
and 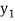 ,
, 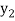 ,
, 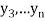 those of
those of 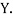
Then 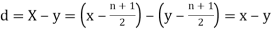
Where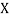 and y are deviations from the mean.
and y are deviations from the mean.
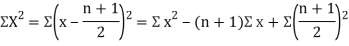
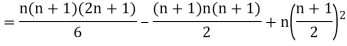
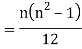
Clearly, 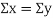 and
and 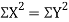
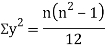
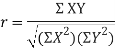
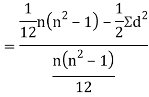
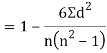
Q14) If X and Y are uncorrelated random variables,  the
the  of correlation between
of correlation between  and
and 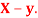
A14)
Let 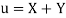 and
and 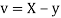
Then 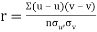
Now 
Similarly 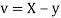
Now 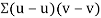
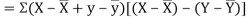
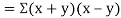
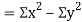
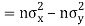
Also 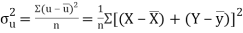
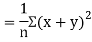
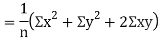
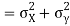 (As
(As 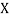 and
and 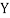 are not correlated, we have
are not correlated, we have 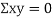 )
)
Similarly 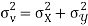
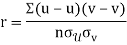
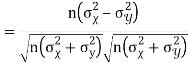
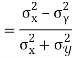
Q15) What do you understand by regression analysis?
A15)
If the scatter diagram indicates some relationship between two variables 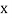 and
and 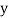 , then the dots of the scatter diagram will be concentrated round a curve. This curve is called the curve of regression. Regression analysis is the method used for estimating the unknown values of one variable corresponding to the known value of another variable.
, then the dots of the scatter diagram will be concentrated round a curve. This curve is called the curve of regression. Regression analysis is the method used for estimating the unknown values of one variable corresponding to the known value of another variable.
Or in other words, Regression is the measure of average relationship between independent and dependent variable
Regression can be used for two or more than two variables.
There are two types of variables in regression analysis.
1. Independent variable
2. Dependent variable
The variable which is used for prediction is called independent variable.
It is known as predictor or regressor.
The variable whose value is predicted by independent variable is called dependent variable or regressed or explained variable.
The scatter diagram shows relationship between independent and dependent variable, then the scatter diagram will be more or less concentrated round a curve, which is called the curve of regression.
When we find the curve as a straight line then it is known as line of regression and the regression is called linear regression.
Note- regression line is the best fit line which expresses the average relation between variables.
Q16) Two variables X and Y are given in the dataset below, find the two lines of regression.
x | 65 | 66 | 67 | 67 | 68 | 69 | 70 | 71 |
y | 66 | 68 | 65 | 69 | 74 | 73 | 72 | 70 |
A16)
The two lines of regression can be expressed as-
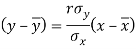
And
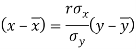
x | y | 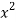 | 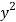 | Xy |
65 | 66 | 4225 | 4356 | 4290 |
66 | 68 | 4356 | 4624 | 4488 |
67 | 65 | 4489 | 4225 | 4355 |
67 | 69 | 4489 | 4761 | 4623 |
68 | 74 | 4624 | 5476 | 5032 |
69 | 73 | 4761 | 5329 | 5037 |
70 | 72 | 4900 | 5184 | 5040 |
71 | 70 | 5041 | 4900 | 4970 |
Sum = 543 | 557 | 36885 | 38855 | 37835 |
Now-
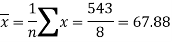
And
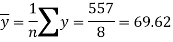
Standard deviation of x-
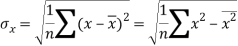

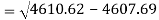
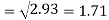
Similarly-
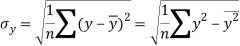
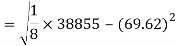
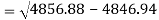
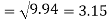
Correlation coefficient-
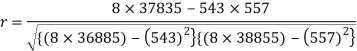
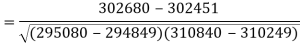
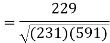
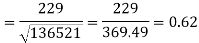
Put these values in regression line equation, we get
Regression line y on x-
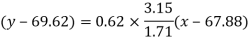
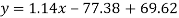
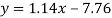
Regression line x on y-