Unit – 2
Solution of linear simultaneous Equations
Q1) Apply Gauss Elimination method to solve the equations:

A1)
Given Check Sum (sum of coefficient and constant)
 -1 …. (I)
-1 …. (I)
 -16 …. (ii)
-16 …. (ii)
 5…. (iii)
5…. (iii)
(I)We eliminate x from (ii) and (iii)
Apply eq(ii)-eq(i) and eq(iii)-3eq(i) we get
 -1 ….(i)
-1 ….(i)
 -15 ….(iv)
-15 ….(iv)
 8 ….(v)
8 ….(v)
(II) We eliminate y from eq(v)
Apply 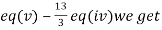
 -1 ….(i)
-1 ….(i)
 -15 ….(iv)
-15 ….(iv)
 73 ….(vi)
73 ….(vi)
(III) Back Substitution we get
From (vi) we get 
From (iv) we get 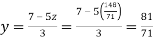
From (i) we get 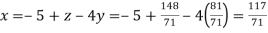
Hence the solution of the given equation is 
Q2) Solve the equation by Gauss Elimination Method:

A2)
Given 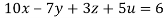
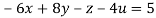


Rewrite the given equation as
 … (i)
… (i)
 ….(ii)
….(ii)
 ….(iii)
….(iii)
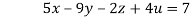 …(iv)
…(iv)
(I) We eliminate x from (ii),(iii) and (iv) we get
Apply eq(ii) + 6eq(i), eq(iii) -3eq(i), eq(iv)-5eq(i) we get
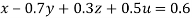 …(i)
…(i)
 ….(v)
….(v)
 ….(vi)
….(vi)
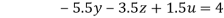 …(vii)
…(vii)
(II) We eliminate y from (vi) and (vii) we get
Apply 3.8 eq(vi)-3.1eq(v) and 3.8eq(vii)+5.5eq(v) we get
 …(i)
…(i)
 ….(v)
….(v)
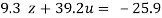 …(viii)
…(viii)
 …(ix)
…(ix)
(III) We eliminate z from eq (ix) we get
Apply 9.3eq (ix) + 8.3eq (viii), we get
 … (i)
… (i)
 ….(v)
….(v)
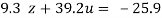 …(viii)
…(viii)
350.74u=350.74
Or u = 1
(IV) Back Substitution
From eq(viii) 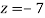
Form eq(v), we get 
From eq(i) , 
Hence the solution of the given equation is x=5, y=4, z=-7 and u=1.
Q3) Apply Gauss Elimination Method to solve the following system of equation:

A3)
Given  … (i)
… (i)
 … (ii)
… (ii)
 … (iii)
… (iii)
(I) We eliminate x from (ii) and (iii)
Apply  we get
we get
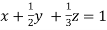 … (i)
… (i)
 … (iv)
… (iv)
 … (v)
… (v)
(II) We eliminate y from (v)
Apply we get
we get
 … (i)
… (i)
 … (vi)
… (vi)
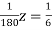 … (vii)
… (vii)
(III) Back substitution
From (vii) 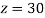
From (vi) 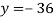
From (i) 
Hence the solution of the equation is 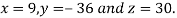
Q4) Solve the system by Gauss Elimination method using partial pivoting


A4)
Given exact solution is 
Given equations are 

Using partial pivoting we rewrite the given equations as
 (1)
(1)
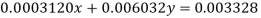 (2)
(2)
Using Gauss elimination method
Multiplying (1) by (-0.0003120/0.5000) + (2) we get

Or 
Substituting value of y in equation (1) we get 
Hence 
Q5) Solve the system of linear equations



A5)
Using partial pivoting by Gauss elimination method we rewrite the given equations as
 (1)
(1)
 (2)
(2)
 (3)
(3)
Apply  and
and 
 (1)
(1)
 (4)
(4)
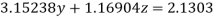 (5)
(5)
Apply  )
)
 (1)
(1)
 (4)
(4)

Or  .
.
Putting value of z in 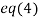 we get
we get 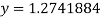 .
.
Putting values of y and z in  we get
we get  .
.
Hence the solution of the equation is  .
.
Q6) Solve the equations-

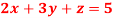

A6)
Let
So that-

3. 
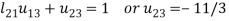
4. 
5. 
So

Thus-
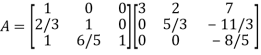
Writing UX = V,
The system of given equations become-

By solving this-
We get-



Therefore the given system becomes-

Which means-

By back substitution, we get the values of x, y and z.
Q7) What is Jacobi’s Iteration method?
A7)
Let us consider the system of simultaneous linear equation

The coefficients of the diagonal elements are larger than the all other coefficients and are non zero. Rewrite the above equation we get

Take the initial approximation  we get the values of the first approximation of
we get the values of the first approximation of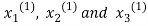 .
.
Q8) Use Jacobi’s method to solve the system of equations:

A8)
Since 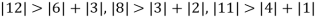
So, we express the unknown with large coefficient in terms of other coefficients.
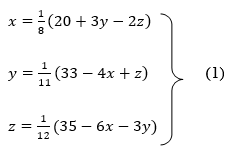
Let the initial approximation be 





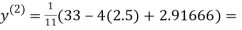 2.35606
2.35606
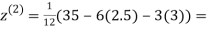 0.91666
0.91666



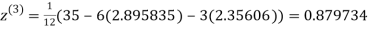

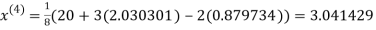
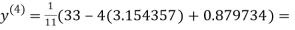 1.932936
1.932936
 0.831912
0.831912

 3.016873
3.016873
 1.969654
1.969654
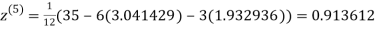

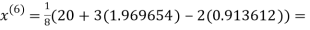 3.010217
3.010217
 1.986010
1.986010

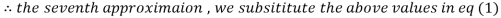

 1.988631
1.988631
 0.915055
0.915055


 1.986532
1.986532
 0.911609
0.911609


 1.985792
1.985792
 0.911547
0.911547


 1.98576
1.98576
 0.911698
0.911698
Since the approximation in ninth and tenth iteration is same up to three decimal places, hence the solution of the given equations is 
Q9) Solve by Jacobi’s Method, the equations

A9)
Given equation can be rewrite in the form
 … (i)
… (i)
 ..(ii)
..(ii)
 ..(iii)
..(iii)
Let the initial approximation be 

Putting these values on the right of the equation (i), (ii) and (iii) and so we get

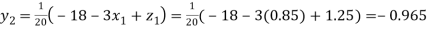

Putting these values on the right of the equation (i), (ii) and (iii) and so we get

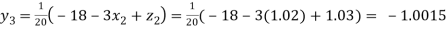
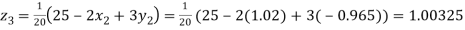
Putting these values on the right of the equation (i), (ii) and (iii) and so we get
 0.90025
0.90025


Putting these values on the right of the equation (i), (ii) and (iii) and so we get



Putting these values on the right of the equation (i), (ii) and (iii) and so we get

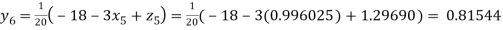

Hence solution approximately is 
Q10) Use Jacobi’s method to solve the system of the equations

A10)
Rewrite the given equations
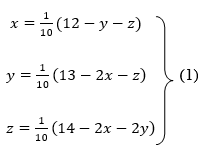
Let the initial approximation be 
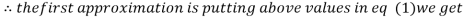
 1.2
1.2
 1.3
1.3

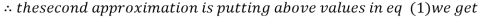


 0.9
0.9



 1.03
1.03

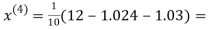 0.9946
0.9946
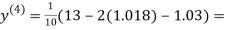 0.9934
0.9934

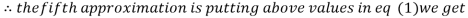
 1.0015
1.0015


Hence the solution of the above equation correct to two decimal places is

Q11) Use Gauss –Seidel Iteration method to solve the system of equations

A11)
Since 
So, we express the unknown of larger coefficient in terms of the unknowns with smaller coefficients.
Rewrite the above system of equations
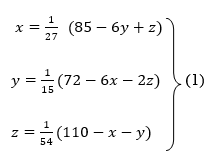
Let the initial approximation be 

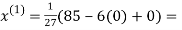 3.14814
3.14814
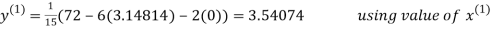


 2.43217
2.43217
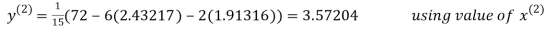


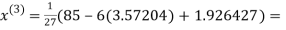 2.42571
2.42571


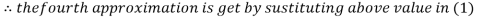
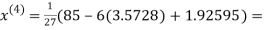 2.4260
2.4260


Hence the solution correct to three decimal places is

Q12) Solve the following system of equations
 By Gauss-Seidel method.
By Gauss-Seidel method.
A12)
Rewrite the given system of equations as

Let the initial approximation be 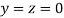


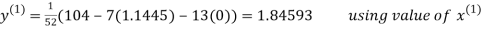



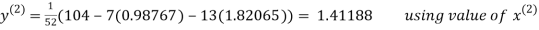




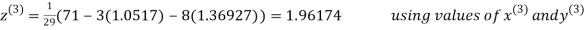




Thus the required solution is 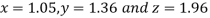
Q13) Solve the following equations by Gauss-Seidel Method




A13)
Rewrite the above system of equations

Let the initial approximation be 


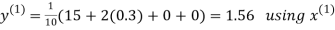
















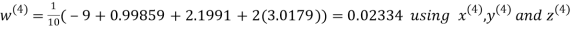
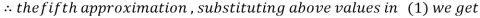




Hence the required solution is 
Unit – 2
Solution of linear simultaneous Equations
Q1) Apply Gauss Elimination method to solve the equations:

A1)
Given Check Sum (sum of coefficient and constant)
 -1 …. (I)
-1 …. (I)
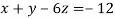 -16 …. (ii)
-16 …. (ii)
 5…. (iii)
5…. (iii)
(I)We eliminate x from (ii) and (iii)
Apply eq(ii)-eq(i) and eq(iii)-3eq(i) we get
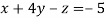 -1 ….(i)
-1 ….(i)
 -15 ….(iv)
-15 ….(iv)
 8 ….(v)
8 ….(v)
(II) We eliminate y from eq(v)
Apply 
 -1 ….(i)
-1 ….(i)
 -15 ….(iv)
-15 ….(iv)
 73 ….(vi)
73 ….(vi)
(III) Back Substitution we get
From (vi) we get 
From (iv) we get 
From (i) we get 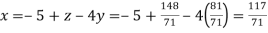
Hence the solution of the given equation is 
Q2) Solve the equation by Gauss Elimination Method:
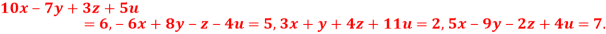
A2)
Given 



Rewrite the given equation as
 … (i)
… (i)
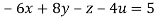 ….(ii)
….(ii)
 ….(iii)
….(iii)
 …(iv)
…(iv)
(I) We eliminate x from (ii),(iii) and (iv) we get
Apply eq(ii) + 6eq(i), eq(iii) -3eq(i), eq(iv)-5eq(i) we get
 …(i)
…(i)
 ….(v)
….(v)
 ….(vi)
….(vi)
 …(vii)
…(vii)
(II) We eliminate y from (vi) and (vii) we get
Apply 3.8 eq(vi)-3.1eq(v) and 3.8eq(vii)+5.5eq(v) we get
 …(i)
…(i)
 ….(v)
….(v)
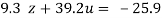 …(viii)
…(viii)
 …(ix)
…(ix)
(III) We eliminate z from eq (ix) we get
Apply 9.3eq (ix) + 8.3eq (viii), we get
 … (i)
… (i)
 ….(v)
….(v)
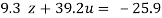 …(viii)
…(viii)
350.74u=350.74
Or u = 1
(IV) Back Substitution
From eq(viii) 
Form eq(v), we get 
From eq(i) , 
Hence the solution of the given equation is x=5, y=4, z=-7 and u=1.
Q3) Apply Gauss Elimination Method to solve the following system of equation:

A3)
Given 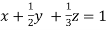 … (i)
… (i)
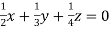 … (ii)
… (ii)
 … (iii)
… (iii)
(I) We eliminate x from (ii) and (iii)
Apply  we get
we get
 … (i)
… (i)
 … (iv)
… (iv)
 … (v)
… (v)
(II) We eliminate y from (v)
Apply we get
we get
 … (i)
… (i)
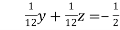 … (vi)
… (vi)
 … (vii)
… (vii)
(III) Back substitution
From (vii) 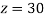
From (vi) 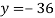
From (i) 
Hence the solution of the equation is 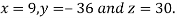
Q4) Solve the system by Gauss Elimination method using partial pivoting


A4)
Given exact solution is 
Given equations are 

Using partial pivoting we rewrite the given equations as
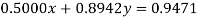 (1)
(1)
 (2)
(2)
Using Gauss elimination method
Multiplying (1) by (-0.0003120/0.5000) + (2) we get

Or 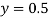
Substituting value of y in equation (1) we get 
Hence 
Q5) Solve the system of linear equations



A5)
Using partial pivoting by Gauss elimination method we rewrite the given equations as
 (1)
(1)
 (2)
(2)
 (3)
(3)
Apply 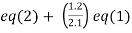 and
and 
 (1)
(1)
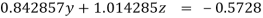 (4)
(4)
 (5)
(5)
Apply 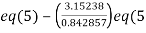 )
)
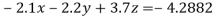 (1)
(1)
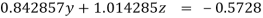 (4)
(4)

Or 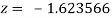 .
.
Putting value of z in  we get
we get 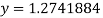 .
.
Putting values of y and z in 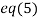 we get
we get  .
.
Hence the solution of the equation is  .
.
Q6) Solve the equations-
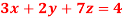

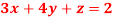
A6)
Let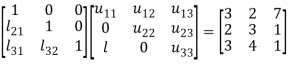
So that-
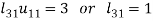
3. 

4. 
5. 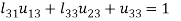
So

Thus-

Writing UX = V,
The system of given equations become-

By solving this-
We get-
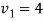

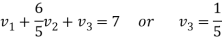
Therefore the given system becomes-

Which means-
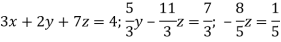
By back substitution, we get the values of x, y and z.
Q7) What is Jacobi’s Iteration method?
A7)
Let us consider the system of simultaneous linear equation

The coefficients of the diagonal elements are larger than the all other coefficients and are non zero. Rewrite the above equation we get

Take the initial approximation 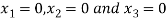 we get the values of the first approximation of
we get the values of the first approximation of .
.
Q8) Use Jacobi’s method to solve the system of equations:
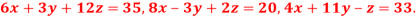
A8)
Since 
So, we express the unknown with large coefficient in terms of other coefficients.
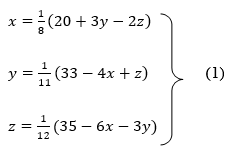
Let the initial approximation be 




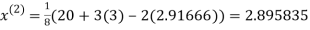
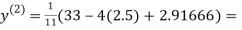 2.35606
2.35606
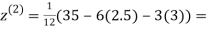 0.91666
0.91666


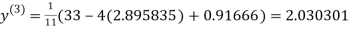



 1.932936
1.932936
 0.831912
0.831912
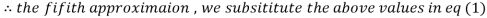
 3.016873
3.016873
 1.969654
1.969654
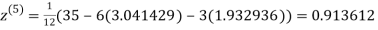

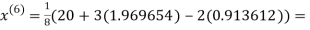 3.010217
3.010217
 1.986010
1.986010



 1.988631
1.988631
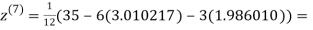 0.915055
0.915055

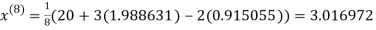
 1.986532
1.986532
 0.911609
0.911609


 1.985792
1.985792
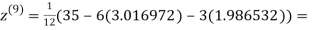 0.911547
0.911547


 1.98576
1.98576
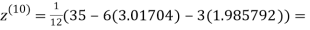 0.911698
0.911698
Since the approximation in ninth and tenth iteration is same up to three decimal places, hence the solution of the given equations is 
Q9) Solve by Jacobi’s Method, the equations

A9)
Given equation can be rewrite in the form
 … (i)
… (i)
 ..(ii)
..(ii)
 ..(iii)
..(iii)
Let the initial approximation be 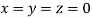

Putting these values on the right of the equation (i), (ii) and (iii) and so we get

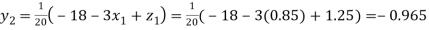
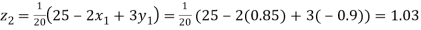
Putting these values on the right of the equation (i), (ii) and (iii) and so we get



Putting these values on the right of the equation (i), (ii) and (iii) and so we get
 0.90025
0.90025


Putting these values on the right of the equation (i), (ii) and (iii) and so we get



Putting these values on the right of the equation (i), (ii) and (iii) and so we get



Hence solution approximately is 
Q10) Use Jacobi’s method to solve the system of the equations

A10)
Rewrite the given equations
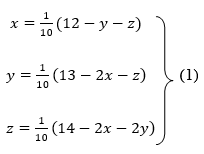
Let the initial approximation be 
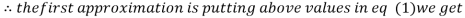
 1.2
1.2
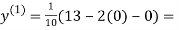 1.3
1.3




 0.9
0.9


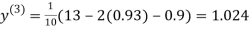
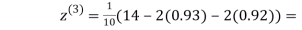 1.03
1.03

 0.9946
0.9946
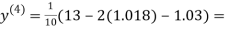 0.9934
0.9934

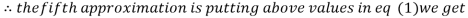
 1.0015
1.0015


Hence the solution of the above equation correct to two decimal places is

Q11) Use Gauss –Seidel Iteration method to solve the system of equations

A11)
Since 
So, we express the unknown of larger coefficient in terms of the unknowns with smaller coefficients.
Rewrite the above system of equations

Let the initial approximation be 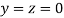

 3.14814
3.14814

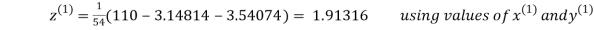

 2.43217
2.43217



 2.42571
2.42571


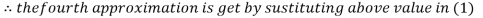
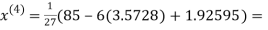 2.4260
2.4260
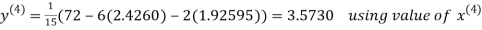

Hence the solution correct to three decimal places is

Q12) Solve the following system of equations
 By Gauss-Seidel method.
By Gauss-Seidel method.
A12)
Rewrite the given system of equations as
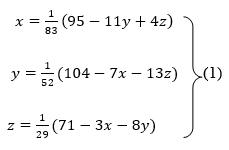
Let the initial approximation be 







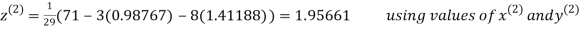








Thus the required solution is 
Q13) Solve the following equations by Gauss-Seidel Method




A13)
Rewrite the above system of equations

Let the initial approximation be 


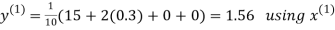



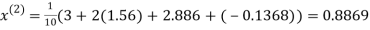
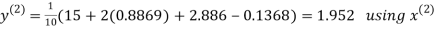




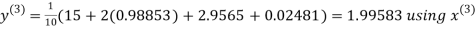
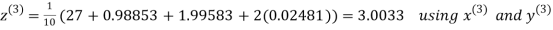


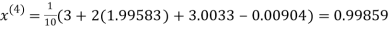


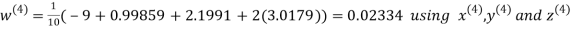
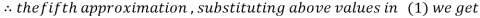

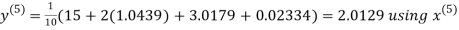


Hence the required solution is 
Unit – 2
Unit – 2
Unit – 2
Unit – 2
Unit – 2
Solution of linear simultaneous Equations
Q1) Apply Gauss Elimination method to solve the equations:

A1)
Given Check Sum (sum of coefficient and constant)
 -1 …. (I)
-1 …. (I)
 -16 …. (ii)
-16 …. (ii)
 5…. (iii)
5…. (iii)
(I)We eliminate x from (ii) and (iii)
Apply eq(ii)-eq(i) and eq(iii)-3eq(i) we get
 -1 ….(i)
-1 ….(i)
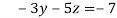 -15 ….(iv)
-15 ….(iv)
 8 ….(v)
8 ….(v)
(II) We eliminate y from eq(v)
Apply 
 -1 ….(i)
-1 ….(i)
 -15 ….(iv)
-15 ….(iv)
 73 ….(vi)
73 ….(vi)
(III) Back Substitution we get
From (vi) we get 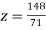
From (iv) we get 
From (i) we get 
Hence the solution of the given equation is 
Q2) Solve the equation by Gauss Elimination Method:

A2)
Given 



Rewrite the given equation as
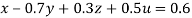 … (i)
… (i)
 ….(ii)
….(ii)
 ….(iii)
….(iii)
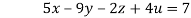 …(iv)
…(iv)
(I) We eliminate x from (ii),(iii) and (iv) we get
Apply eq(ii) + 6eq(i), eq(iii) -3eq(i), eq(iv)-5eq(i) we get
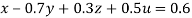 …(i)
…(i)
 ….(v)
….(v)
 ….(vi)
….(vi)
 …(vii)
…(vii)
(II) We eliminate y from (vi) and (vii) we get
Apply 3.8 eq(vi)-3.1eq(v) and 3.8eq(vii)+5.5eq(v) we get
 …(i)
…(i)
 ….(v)
….(v)
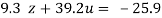 …(viii)
…(viii)
 …(ix)
…(ix)
(III) We eliminate z from eq (ix) we get
Apply 9.3eq (ix) + 8.3eq (viii), we get
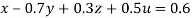 … (i)
… (i)
 ….(v)
….(v)
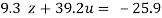 …(viii)
…(viii)
350.74u=350.74
Or u = 1
(IV) Back Substitution
From eq(viii) 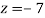
Form eq(v), we get 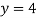
From eq(i) , 
Hence the solution of the given equation is x=5, y=4, z=-7 and u=1.
Q3) Apply Gauss Elimination Method to solve the following system of equation:

A3)
Given  … (i)
… (i)
 … (ii)
… (ii)
 … (iii)
… (iii)
(I) We eliminate x from (ii) and (iii)
Apply 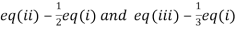 we get
we get
 … (i)
… (i)
 … (iv)
… (iv)
 … (v)
… (v)
(II) We eliminate y from (v)
Apply we get
we get
 … (i)
… (i)
 … (vi)
… (vi)
 … (vii)
… (vii)
(III) Back substitution
From (vii) 
From (vi) 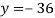
From (i) 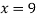
Hence the solution of the equation is 
Q4) Solve the system by Gauss Elimination method using partial pivoting


A4)
Given exact solution is 
Given equations are 
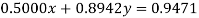
Using partial pivoting we rewrite the given equations as
 (1)
(1)
 (2)
(2)
Using Gauss elimination method
Multiplying (1) by (-0.0003120/0.5000) + (2) we get

Or 
Substituting value of y in equation (1) we get 
Hence 
Q5) Solve the system of linear equations

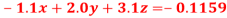

A5)
Using partial pivoting by Gauss elimination method we rewrite the given equations as
 (1)
(1)
 (2)
(2)
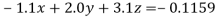 (3)
(3)
Apply  and
and 
 (1)
(1)
 (4)
(4)
 (5)
(5)
Apply  )
)
 (1)
(1)
 (4)
(4)

Or  .
.
Putting value of z in  we get
we get  .
.
Putting values of y and z in  we get
we get  .
.
Hence the solution of the equation is  .
.
Q6) Solve the equations-

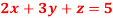
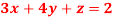
A6)
Let
So that-

3. 

4. 
5. 
So

Thus-

Writing UX = V,
The system of given equations become-
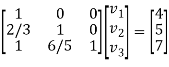
By solving this-
We get-

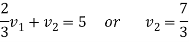

Therefore the given system becomes-

Which means-

By back substitution, we get the values of x, y and z.
Q7) What is Jacobi’s Iteration method?
A7)
Let us consider the system of simultaneous linear equation

The coefficients of the diagonal elements are larger than the all other coefficients and are non zero. Rewrite the above equation we get

Take the initial approximation  we get the values of the first approximation of
we get the values of the first approximation of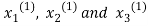 .
.
Q8) Use Jacobi’s method to solve the system of equations:

A8)
Since 
So, we express the unknown with large coefficient in terms of other coefficients.

Let the initial approximation be 
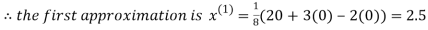

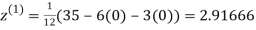
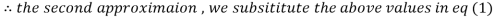
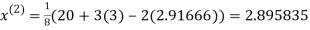
 2.35606
2.35606
 0.91666
0.91666
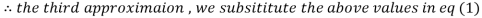


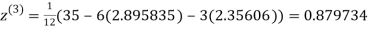


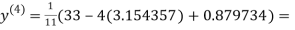 1.932936
1.932936
 0.831912
0.831912
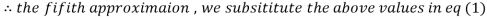
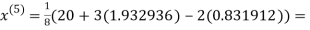 3.016873
3.016873
 1.969654
1.969654
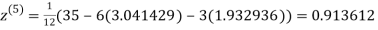

 3.010217
3.010217
 1.986010
1.986010



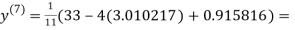 1.988631
1.988631
 0.915055
0.915055
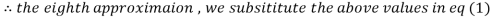

 1.986532
1.986532
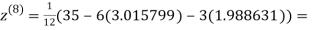 0.911609
0.911609


 1.985792
1.985792
 0.911547
0.911547

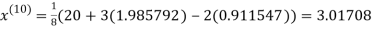
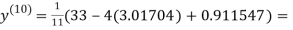 1.98576
1.98576
 0.911698
0.911698
Since the approximation in ninth and tenth iteration is same up to three decimal places, hence the solution of the given equations is 
Q9) Solve by Jacobi’s Method, the equations
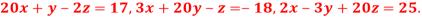
A9)
Given equation can be rewrite in the form
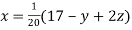 … (i)
… (i)
 ..(ii)
..(ii)
 ..(iii)
..(iii)
Let the initial approximation be 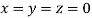

Putting these values on the right of the equation (i), (ii) and (iii) and so we get



Putting these values on the right of the equation (i), (ii) and (iii) and so we get

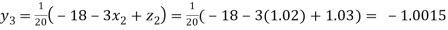
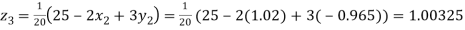
Putting these values on the right of the equation (i), (ii) and (iii) and so we get
 0.90025
0.90025
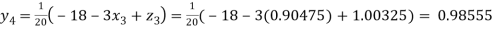

Putting these values on the right of the equation (i), (ii) and (iii) and so we get



Putting these values on the right of the equation (i), (ii) and (iii) and so we get



Hence solution approximately is 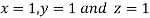
Q10) Use Jacobi’s method to solve the system of the equations

A10)
Rewrite the given equations

Let the initial approximation be 

 1.2
1.2
 1.3
1.3




 0.9
0.9



 1.03
1.03

 0.9946
0.9946
 0.9934
0.9934

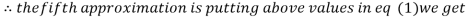
 1.0015
1.0015


Hence the solution of the above equation correct to two decimal places is

Q11) Use Gauss –Seidel Iteration method to solve the system of equations

A11)
Since 
So, we express the unknown of larger coefficient in terms of the unknowns with smaller coefficients.
Rewrite the above system of equations
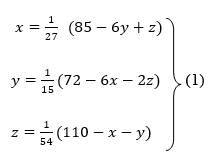
Let the initial approximation be 
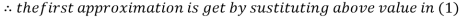
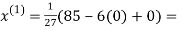 3.14814
3.14814

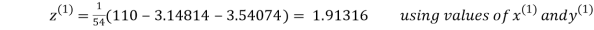

 2.43217
2.43217


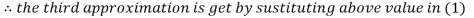
 2.42571
2.42571



 2.4260
2.4260
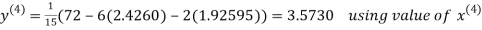

Hence the solution correct to three decimal places is

Q12) Solve the following system of equations
 By Gauss-Seidel method.
By Gauss-Seidel method.
A12)
Rewrite the given system of equations as
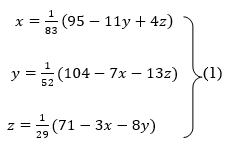
Let the initial approximation be 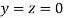













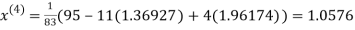


Thus the required solution is 
Q13) Solve the following equations by Gauss-Seidel Method




A13)
Rewrite the above system of equations

Let the initial approximation be 




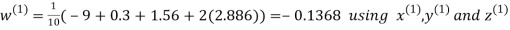


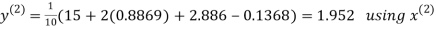






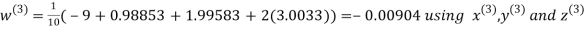








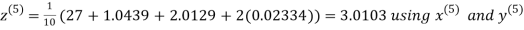
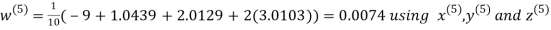
Hence the required solution is 





