Unit – 5
Linear Equations and Matrix Theory
Q1) What do you understand by a matrix?
A1)
A matrix is a rectangular arrangement of the numbers.
These numbers inside the matrix are known as elements of the matrix.
A matrix ‘A’ is expressed as-
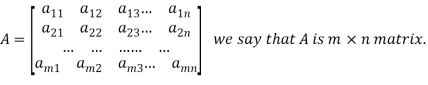
The vertical elements are called columns and the horizontal elements are rows of the matrix.
The order of matrix A is m by n or (m× n)
Q2) What do you understand by the transpose of a matrix?
A2)
The matrix obtained from any given matrix A , by interchanging rows and columns is called the transpose of A and is denoted by 

The transpose of matrix 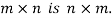 Also
Also 
Q3) What is the trace of a matrix?
A3)
Suppose A be a square matrix, then the sum of its diagonal elements is known as trace of the matrix.
Example- If we have a matrix A-
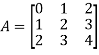
Then the trace of A = 0 + 2 + 4 = 6
Q4) Find the rank of a matrix M by echelon form.
M = 
A4)
First we will convert the matrix M into echelon form,
M = 
Apply,  , we get
, we get
M = 
Apply  , we get
, we get
M = 
Apply 
M = 
We can see that, in this echelon form of matrix, the number of non – zero rows is 3.
So that the rank of matrix X will be 3.
Q5) Find the rank of a matrix A by echelon form.
A = 
A5)
Convert the matrix A into echelon form,
A = 
Apply 
A = 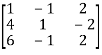
Apply  , we get
, we get
A = 
Apply  , we get
, we get
A = 
Apply  ,
,
A = 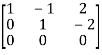
Apply 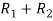 ,
,
A = 
Therefore the rank of the matrix will be 2.
Q6) What is characteristic equation?
A6)
Suppose we have A =  be an n × n matrix , then
be an n × n matrix , then
Characteristic equation- The equation | = 0 is called the characteristic equation of A , where |
= 0 is called the characteristic equation of A , where |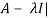 is called characteristic matrix of A. Here I is the identity matrix.
is called characteristic matrix of A. Here I is the identity matrix.
The determinant | is called the characteristic polynomial of A.
is called the characteristic polynomial of A.
Characteristic roots-the roots of the characteristic equation are known as characteristic roots or Eigen values or characteristic values.
Q7) Find the characteristic equation of the matrix A:
A = 
A7)
The characteristic equation will be-
| = 0
= 0
 = 0
= 0
On solving the determinant, we get
(4-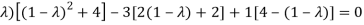
Or 
On solving we get,
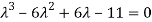
Which is the characteristic equation of matrix A.
Q8) Find the characteristic equation and characteristic roots of the matrix A:
A = 
A8)
We know that the characteristic equation of the matrix A will be-
| = 0
= 0
So that matrix A becomes,
 = 0
= 0
Which gives , on solving
(1- = 0
= 0
Or 
Or (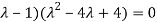
Which is the characteristic equation of matrix A.
The characteristic roots will be,
( (
(
(
(
Values of 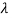 are-
are-

These are the characteristic roots of matrix A.
Q9) Find the characteristic equation and characteristic roots of the matrix A:
A = 
A9)
We know that, the characteristic equation is-
| = 0
= 0
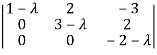 = 0
= 0
Which gives,
(1-
Characteristic roots are- 
Q10) What do you understand by Eigen values and Eigen vectors?
A10)
Let A is a square matrix of order n. The equation formed by

Where I is an identity matrix of order n and  is unknown. It is called characteristic equation of the matrix A.
is unknown. It is called characteristic equation of the matrix A.

The values of the  are called the root of the characteristic equation, they are also known as characteristics roots or latent root or Eigen values of the matrix A.
are called the root of the characteristic equation, they are also known as characteristics roots or latent root or Eigen values of the matrix A.
Corresponding to each Eigen value there exist vectors X,

Called the characteristics vectors or latent vectors or Eigen vectors of the matrix A.
Q11) Write down the properties of Eigen values.
A11)
Properties of Eigen Values:
- The sum of the principal diagonal element of the matrix is equal to the sum of the all Eigen values of the matrix.
Let A be a matrix of order 3 then 
2. The determinant of the matrix A is equal to the product of the all Eigen values of the matrix then  .
.
3. If  is the Eigen value of the matrix A then 1/
is the Eigen value of the matrix A then 1/ is the Eigen value of the
is the Eigen value of the  .
.
4. If  is the Eigen value of an orthogonal matrix, then 1/
is the Eigen value of an orthogonal matrix, then 1/ is also its Eigen value.
is also its Eigen value.
If 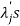 are the Eigen values of the matrix A then
are the Eigen values of the matrix A then  has the Eigen values
has the Eigen values 
Q12) Find the sum and the product of the Eigen values of  ?
?
A12)
The sum of Eigen values = the sum of the diagonal elements
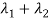 =1+(-1)=0
=1+(-1)=0
The product of the Eigen values is the determinant of the matrix

On solving above equations we get 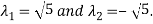
Q13) Find out the Eigen values and Eigen vectors of  ?
?
A13)
The Characteristics equation is given by 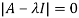

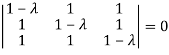

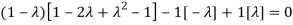


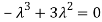
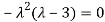
Or 
Hence the Eigen values are 0,0 and 3.
The Eigen vector corresponding to Eigen value 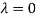 is
is

Where X is the column matrix of order 3 i.e.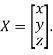

This implies that 
Here number of unknowns are 3 and number of equation is 1.
Hence we have (3-1)=2 linearly independent solutions.
Let 
Thus the Eigen vectors corresponding to the Eigen value 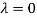 are (-1,1,0) and (-2,1,1).
are (-1,1,0) and (-2,1,1).
The Eigen vector corresponding to Eigen value  is
is
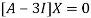
Where X is the column matrix of order 3 i.e.

This implies that 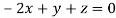

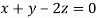
Taking last two equations we get
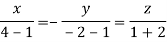
Or 
Thus the Eigen vectors corresponding to the Eigen value  are (3,3,3).
are (3,3,3).
Hence the three Eigen vectors obtained are (-1,1,0), (-2,1,1) and (3,3,3).
Q14) Find out the Eigen values and Eigen vectors of 
A14)
Let A =
The characteristics equation of A is  .
.


Or 
Or 
Or 
Or 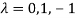
The Eigen vector corresponding to Eigen value  is
is

Where X is the column matrix of order 3 i.e.

Or 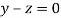


On solving we get 
Thus the Eigen vectors corresponding to the Eigen value 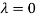 is (1,1,1).
is (1,1,1).
The Eigen vector corresponding to Eigen value 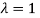 is
is

Where X is the column matrix of order 3 i.e.

Or 


On solving  or
or  .
.
Thus the Eigen vectors corresponding to the Eigen value 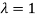 is (0,0,2).
is (0,0,2).
The Eigen vector corresponding to Eigen value 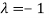 is
is

Where X is the column matrix of order 3 i.e.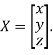

Or 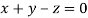
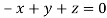

On solving we get  or
or 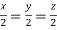 .
.
Thus the Eigen vectors corresponding to the Eigen value  is (2,2,2).
is (2,2,2).
Hence three Eigen vectors are (1,1,1), (0,0,2) and (2,2,2).
Q15) Check whether the following system of linear equations is consistent of not.
2x + 6y = -11
6x + 20y – 6z = -3
6y – 18z = -1
A15)
Write the above system of linear equations in augmented matrix form,

Apply 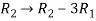 , we get
, we get

Apply 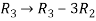

Here the rank of C is 3 and the rank of A is 2
Q16) The mapping  defined by-
defined by-
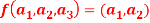
Is a linear transformation  .
.
What is the kernel of this linear transformation.
A16)
Let  be any two elements of
be any two elements of 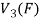
Let a, b be any two elements of F.
We have
 (
(


 =
= 

So that f is a linear transformation.
To show that f is onto  . Let
. Let  be any elements
be any elements  .
.
Then  and we have
and we have 
So that f is onto 
Therefore f is homomorphism of  onto
onto  .
.
If W is the kernel of this homomorphism then 
We have
∀
Also if  then
then 
Implies 
Therefore 
Hence W is the kernel of f.
Q17)  be the linear operator defined by F(x, y) = (2x + 3y, 4x – 5y).
be the linear operator defined by F(x, y) = (2x + 3y, 4x – 5y).
Find the matrix representation of F relative to the basis S = {  } = {(1, 2), (2, 5)}
} = {(1, 2), (2, 5)}
A17)
(1) First find F( , and then write it as a linear combination of the basis vectors
, and then write it as a linear combination of the basis vectors  and
and  . (For notational convenience, we use column vectors.) We have
. (For notational convenience, we use column vectors.) We have

And
X + 2y = 8
2x + 5y = -6
Solve the system to obtain x = 52, y =-22. Hence,

Now

X + 2y = 19
2x + 5y = -17
Solve the system to obtain x = 129, y =-55. Hence,

Now write the coordinates of 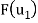 and
and  as columns to obtain the matrix
as columns to obtain the matrix

Unit – 5
Linear Equations and Matrix Theory
Q1) What do you understand by a matrix?
A1)
A matrix is a rectangular arrangement of the numbers.
These numbers inside the matrix are known as elements of the matrix.
A matrix ‘A’ is expressed as-

The vertical elements are called columns and the horizontal elements are rows of the matrix.
The order of matrix A is m by n or (m× n)
Q2) What do you understand by the transpose of a matrix?
A2)
The matrix obtained from any given matrix A , by interchanging rows and columns is called the transpose of A and is denoted by 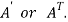

The transpose of matrix  Also
Also 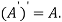
Q3) What is the trace of a matrix?
A3)
Suppose A be a square matrix, then the sum of its diagonal elements is known as trace of the matrix.
Example- If we have a matrix A-

Then the trace of A = 0 + 2 + 4 = 6
Q4) Find the rank of a matrix M by echelon form.
M = 
A4)
First we will convert the matrix M into echelon form,
M = 
Apply,  , we get
, we get
M = 
Apply  , we get
, we get
M = 
Apply 
M = 
We can see that, in this echelon form of matrix, the number of non – zero rows is 3.
So that the rank of matrix X will be 3.
Q5) Find the rank of a matrix A by echelon form.
A = 
A5)
Convert the matrix A into echelon form,
A = 
Apply 
A = 
Apply  , we get
, we get
A = 
Apply  , we get
, we get
A = 
Apply  ,
,
A = 
Apply  ,
,
A = 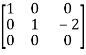
Therefore the rank of the matrix will be 2.
Q6) What is characteristic equation?
A6)
Suppose we have A =  be an n × n matrix , then
be an n × n matrix , then
Characteristic equation- The equation | = 0 is called the characteristic equation of A , where |
= 0 is called the characteristic equation of A , where | is called characteristic matrix of A. Here I is the identity matrix.
is called characteristic matrix of A. Here I is the identity matrix.
The determinant | is called the characteristic polynomial of A.
is called the characteristic polynomial of A.
Characteristic roots-the roots of the characteristic equation are known as characteristic roots or Eigen values or characteristic values.
Q7) Find the characteristic equation of the matrix A:
A = 
A7)
The characteristic equation will be-
| = 0
= 0
 = 0
= 0
On solving the determinant, we get
(4-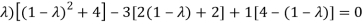
Or 
On solving we get,
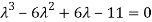
Which is the characteristic equation of matrix A.
Q8) Find the characteristic equation and characteristic roots of the matrix A:
A = 
A8)
We know that the characteristic equation of the matrix A will be-
| = 0
= 0
So that matrix A becomes,
 = 0
= 0
Which gives , on solving
(1- = 0
= 0
Or 
Or (
Which is the characteristic equation of matrix A.
The characteristic roots will be,
( (
(
(
(
Values of 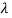 are-
are-
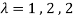
These are the characteristic roots of matrix A.
Q9) Find the characteristic equation and characteristic roots of the matrix A:
A = 
A9)
We know that, the characteristic equation is-
| = 0
= 0
 = 0
= 0
Which gives,
(1-
Characteristic roots are- 
Q10) What do you understand by Eigen values and Eigen vectors?
A10)
Let A is a square matrix of order n. The equation formed by

Where I is an identity matrix of order n and  is unknown. It is called characteristic equation of the matrix A.
is unknown. It is called characteristic equation of the matrix A.

The values of the  are called the root of the characteristic equation, they are also known as characteristics roots or latent root or Eigen values of the matrix A.
are called the root of the characteristic equation, they are also known as characteristics roots or latent root or Eigen values of the matrix A.
Corresponding to each Eigen value there exist vectors X,

Called the characteristics vectors or latent vectors or Eigen vectors of the matrix A.
Q11) Write down the properties of Eigen values.
A11)
Properties of Eigen Values:
- The sum of the principal diagonal element of the matrix is equal to the sum of the all Eigen values of the matrix.
Let A be a matrix of order 3 then 
2. The determinant of the matrix A is equal to the product of the all Eigen values of the matrix then  .
.
3. If  is the Eigen value of the matrix A then 1/
is the Eigen value of the matrix A then 1/ is the Eigen value of the
is the Eigen value of the  .
.
4. If  is the Eigen value of an orthogonal matrix, then 1/
is the Eigen value of an orthogonal matrix, then 1/ is also its Eigen value.
is also its Eigen value.
If  are the Eigen values of the matrix A then
are the Eigen values of the matrix A then  has the Eigen values
has the Eigen values 
Q12) Find the sum and the product of the Eigen values of  ?
?
A12)
The sum of Eigen values = the sum of the diagonal elements
 =1+(-1)=0
=1+(-1)=0
The product of the Eigen values is the determinant of the matrix
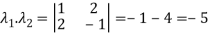
On solving above equations we get 
Q13) Find out the Eigen values and Eigen vectors of  ?
?
A13)
The Characteristics equation is given by 







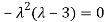
Or 
Hence the Eigen values are 0,0 and 3.
The Eigen vector corresponding to Eigen value 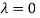 is
is

Where X is the column matrix of order 3 i.e.

This implies that 
Here number of unknowns are 3 and number of equation is 1.
Hence we have (3-1)=2 linearly independent solutions.
Let 
Thus the Eigen vectors corresponding to the Eigen value  are (-1,1,0) and (-2,1,1).
are (-1,1,0) and (-2,1,1).
The Eigen vector corresponding to Eigen value  is
is

Where X is the column matrix of order 3 i.e.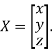

This implies that 


Taking last two equations we get
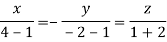
Or 
Thus the Eigen vectors corresponding to the Eigen value 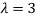 are (3,3,3).
are (3,3,3).
Hence the three Eigen vectors obtained are (-1,1,0), (-2,1,1) and (3,3,3).
Q14) Find out the Eigen values and Eigen vectors of 
A14)
Let A =
The characteristics equation of A is 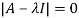 .
.


Or 
Or 
Or 
Or 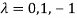
The Eigen vector corresponding to Eigen value  is
is

Where X is the column matrix of order 3 i.e.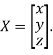

Or 


On solving we get 
Thus the Eigen vectors corresponding to the Eigen value  is (1,1,1).
is (1,1,1).
The Eigen vector corresponding to Eigen value  is
is

Where X is the column matrix of order 3 i.e.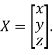
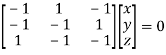
Or 


On solving  or
or  .
.
Thus the Eigen vectors corresponding to the Eigen value  is (0,0,2).
is (0,0,2).
The Eigen vector corresponding to Eigen value 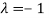 is
is

Where X is the column matrix of order 3 i.e.

Or 


On solving we get  or
or 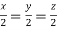 .
.
Thus the Eigen vectors corresponding to the Eigen value  is (2,2,2).
is (2,2,2).
Hence three Eigen vectors are (1,1,1), (0,0,2) and (2,2,2).
Q15) Check whether the following system of linear equations is consistent of not.
2x + 6y = -11
6x + 20y – 6z = -3
6y – 18z = -1
A15)
Write the above system of linear equations in augmented matrix form,

Apply  , we get
, we get
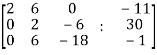
Apply 

Here the rank of C is 3 and the rank of A is 2
Q16) The mapping  defined by-
defined by-
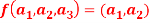
Is a linear transformation  .
.
What is the kernel of this linear transformation.
A16)
Let 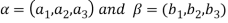 be any two elements of
be any two elements of 
Let a, b be any two elements of F.
We have
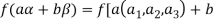 (
(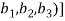


 =
= 
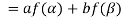
So that f is a linear transformation.
To show that f is onto  . Let
. Let 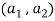 be any elements
be any elements  .
.
Then  and we have
and we have 
So that f is onto 
Therefore f is homomorphism of  onto
onto  .
.
If W is the kernel of this homomorphism then 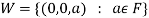
We have
∀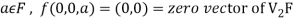
Also if 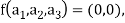 then
then 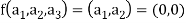
Implies 
Therefore 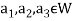
Hence W is the kernel of f.
Q17)  be the linear operator defined by F(x, y) = (2x + 3y, 4x – 5y).
be the linear operator defined by F(x, y) = (2x + 3y, 4x – 5y).
Find the matrix representation of F relative to the basis S = { 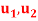 } = {(1, 2), (2, 5)}
} = {(1, 2), (2, 5)}
A17)
(1) First find F(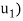 , and then write it as a linear combination of the basis vectors
, and then write it as a linear combination of the basis vectors  and
and  . (For notational convenience, we use column vectors.) We have
. (For notational convenience, we use column vectors.) We have
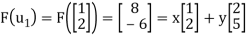
And
X + 2y = 8
2x + 5y = -6
Solve the system to obtain x = 52, y =-22. Hence,

Now

X + 2y = 19
2x + 5y = -17
Solve the system to obtain x = 129, y =-55. Hence,

Now write the coordinates of  and
and  as columns to obtain the matrix
as columns to obtain the matrix

Unit – 5
Unit – 5
Unit – 5
Unit – 5
Unit – 5
Unit – 5
Linear Equations and Matrix Theory
Q1) What do you understand by a matrix?
A1)
A matrix is a rectangular arrangement of the numbers.
These numbers inside the matrix are known as elements of the matrix.
A matrix ‘A’ is expressed as-

The vertical elements are called columns and the horizontal elements are rows of the matrix.
The order of matrix A is m by n or (m× n)
Q2) What do you understand by the transpose of a matrix?
A2)
The matrix obtained from any given matrix A , by interchanging rows and columns is called the transpose of A and is denoted by 

The transpose of matrix  Also
Also 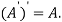
Q3) What is the trace of a matrix?
A3)
Suppose A be a square matrix, then the sum of its diagonal elements is known as trace of the matrix.
Example- If we have a matrix A-

Then the trace of A = 0 + 2 + 4 = 6
Q4) Find the rank of a matrix M by echelon form.
M = 
A4)
First we will convert the matrix M into echelon form,
M = 
Apply,  , we get
, we get
M = 
Apply 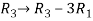 , we get
, we get
M = 
Apply 
M = 
We can see that, in this echelon form of matrix, the number of non – zero rows is 3.
So that the rank of matrix X will be 3.
Q5) Find the rank of a matrix A by echelon form.
A = 
A5)
Convert the matrix A into echelon form,
A = 
Apply 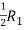
A = 
Apply  , we get
, we get
A = 
Apply  , we get
, we get
A = 
Apply  ,
,
A = 
Apply  ,
,
A = 
Therefore the rank of the matrix will be 2.
Q6) What is characteristic equation?
A6)
Suppose we have A =  be an n × n matrix , then
be an n × n matrix , then
Characteristic equation- The equation | = 0 is called the characteristic equation of A , where |
= 0 is called the characteristic equation of A , where | is called characteristic matrix of A. Here I is the identity matrix.
is called characteristic matrix of A. Here I is the identity matrix.
The determinant | is called the characteristic polynomial of A.
is called the characteristic polynomial of A.
Characteristic roots-the roots of the characteristic equation are known as characteristic roots or Eigen values or characteristic values.
Q7) Find the characteristic equation of the matrix A:
A = 
A7)
The characteristic equation will be-
| = 0
= 0
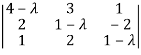 = 0
= 0
On solving the determinant, we get
(4-
Or 
On solving we get,

Which is the characteristic equation of matrix A.
Q8) Find the characteristic equation and characteristic roots of the matrix A:
A = 
A8)
We know that the characteristic equation of the matrix A will be-
| = 0
= 0
So that matrix A becomes,
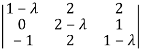 = 0
= 0
Which gives , on solving
(1- = 0
= 0
Or 
Or (
Which is the characteristic equation of matrix A.
The characteristic roots will be,
( (
(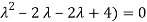
(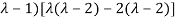
(
Values of  are-
are-

These are the characteristic roots of matrix A.
Q9) Find the characteristic equation and characteristic roots of the matrix A:
A = 
A9)
We know that, the characteristic equation is-
| = 0
= 0
 = 0
= 0
Which gives,
(1-
Characteristic roots are- 
Q10) What do you understand by Eigen values and Eigen vectors?
A10)
Let A is a square matrix of order n. The equation formed by

Where I is an identity matrix of order n and  is unknown. It is called characteristic equation of the matrix A.
is unknown. It is called characteristic equation of the matrix A.
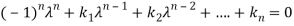
The values of the  are called the root of the characteristic equation, they are also known as characteristics roots or latent root or Eigen values of the matrix A.
are called the root of the characteristic equation, they are also known as characteristics roots or latent root or Eigen values of the matrix A.
Corresponding to each Eigen value there exist vectors X,

Called the characteristics vectors or latent vectors or Eigen vectors of the matrix A.
Q11) Write down the properties of Eigen values.
A11)
Properties of Eigen Values:
- The sum of the principal diagonal element of the matrix is equal to the sum of the all Eigen values of the matrix.
Let A be a matrix of order 3 then 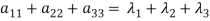
2. The determinant of the matrix A is equal to the product of the all Eigen values of the matrix then  .
.
3. If  is the Eigen value of the matrix A then 1/
is the Eigen value of the matrix A then 1/ is the Eigen value of the
is the Eigen value of the 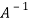 .
.
4. If  is the Eigen value of an orthogonal matrix, then 1/
is the Eigen value of an orthogonal matrix, then 1/ is also its Eigen value.
is also its Eigen value.
If  are the Eigen values of the matrix A then
are the Eigen values of the matrix A then  has the Eigen values
has the Eigen values 
Q12) Find the sum and the product of the Eigen values of  ?
?
A12)
The sum of Eigen values = the sum of the diagonal elements
 =1+(-1)=0
=1+(-1)=0
The product of the Eigen values is the determinant of the matrix
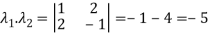
On solving above equations we get 
Q13) Find out the Eigen values and Eigen vectors of  ?
?
A13)
The Characteristics equation is given by 



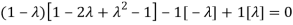
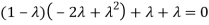


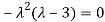
Or 
Hence the Eigen values are 0,0 and 3.
The Eigen vector corresponding to Eigen value  is
is

Where X is the column matrix of order 3 i.e.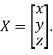

This implies that 
Here number of unknowns are 3 and number of equation is 1.
Hence we have (3-1)=2 linearly independent solutions.
Let 
Thus the Eigen vectors corresponding to the Eigen value  are (-1,1,0) and (-2,1,1).
are (-1,1,0) and (-2,1,1).
The Eigen vector corresponding to Eigen value  is
is

Where X is the column matrix of order 3 i.e.

This implies that 


Taking last two equations we get

Or 
Thus the Eigen vectors corresponding to the Eigen value 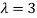 are (3,3,3).
are (3,3,3).
Hence the three Eigen vectors obtained are (-1,1,0), (-2,1,1) and (3,3,3).
Q14) Find out the Eigen values and Eigen vectors of 
A14)
Let A =
The characteristics equation of A is 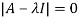 .
.

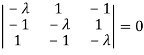
Or 
Or 
Or 
Or 
The Eigen vector corresponding to Eigen value 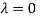 is
is

Where X is the column matrix of order 3 i.e.

Or 


On solving we get 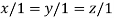
Thus the Eigen vectors corresponding to the Eigen value 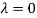 is (1,1,1).
is (1,1,1).
The Eigen vector corresponding to Eigen value 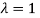 is
is

Where X is the column matrix of order 3 i.e.

Or 
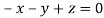

On solving  or
or 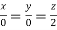 .
.
Thus the Eigen vectors corresponding to the Eigen value 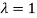 is (0,0,2).
is (0,0,2).
The Eigen vector corresponding to Eigen value  is
is

Where X is the column matrix of order 3 i.e.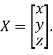

Or 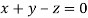


On solving we get  or
or  .
.
Thus the Eigen vectors corresponding to the Eigen value  is (2,2,2).
is (2,2,2).
Hence three Eigen vectors are (1,1,1), (0,0,2) and (2,2,2).
Q15) Check whether the following system of linear equations is consistent of not.
2x + 6y = -11
6x + 20y – 6z = -3
6y – 18z = -1
A15)
Write the above system of linear equations in augmented matrix form,

Apply  , we get
, we get

Apply 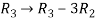

Here the rank of C is 3 and the rank of A is 2
Q16) The mapping 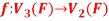 defined by-
defined by-

Is a linear transformation  .
.
What is the kernel of this linear transformation.
A16)
Let  be any two elements of
be any two elements of 
Let a, b be any two elements of F.
We have
 (
(


 =
= 

So that f is a linear transformation.
To show that f is onto  . Let
. Let  be any elements
be any elements  .
.
Then  and we have
and we have 
So that f is onto 
Therefore f is homomorphism of 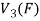 onto
onto  .
.
If W is the kernel of this homomorphism then 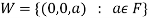
We have
∀
Also if  then
then 
Implies 
Therefore 
Hence W is the kernel of f.
Q17)  be the linear operator defined by F(x, y) = (2x + 3y, 4x – 5y).
be the linear operator defined by F(x, y) = (2x + 3y, 4x – 5y).
Find the matrix representation of F relative to the basis S = {  } = {(1, 2), (2, 5)}
} = {(1, 2), (2, 5)}
A17)
(1) First find F( , and then write it as a linear combination of the basis vectors
, and then write it as a linear combination of the basis vectors  and
and  . (For notational convenience, we use column vectors.) We have
. (For notational convenience, we use column vectors.) We have

And
X + 2y = 8
2x + 5y = -6
Solve the system to obtain x = 52, y =-22. Hence,

Now
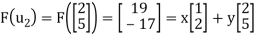
X + 2y = 19
2x + 5y = -17
Solve the system to obtain x = 129, y =-55. Hence,

Now write the coordinates of  and
and  as columns to obtain the matrix
as columns to obtain the matrix
