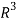Unit – 6
Vector space
Q1) Define vector space.
A1)
Let ‘F’ be any given field, then a given set V is said to be a vector space if-
1. There is a defined composition in ‘V’. This composition called addition of vectors which is denoted by ‘+’
2. There is a defined an external composition in ‘V’ over ‘F’. That will be denoted by scalar multiplication.
3. The two compositions satisfy the following conditions-
(a) 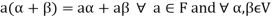
(b) 
(c) 
(d) If  then 1 is the unity element of the field F.
then 1 is the unity element of the field F.
If V is a vector space over the field F, then we will denote vector space as V(F).
Q2) The set of all  matrices with their elements as real numbers is a vector space over the field F of real numbers with respect to addition of matrices as addition of vectors and multiplication of a matrix by a scalar as scalar multiplication.
matrices with their elements as real numbers is a vector space over the field F of real numbers with respect to addition of matrices as addition of vectors and multiplication of a matrix by a scalar as scalar multiplication.
A2)
V is an abelian group with respect to addition of matrices in groups.
The null matrix of m by n is the additive identity of this group.
If  then
then  as
as 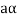 is also the matrix of m by n with elements of real numbers.
is also the matrix of m by n with elements of real numbers.
So that V is closed with respect to scalar multiplication.
We conclude that from matrices-
1. 
2. 
3. 
4. 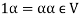 Where 1 is the unity element of F.
Where 1 is the unity element of F.
Therefore we can say that V (F) is a vector space.
Q3) The vector space of all polynomials over a field F. Prove.
A3)
Suppose F[x] represents the set of all polynomials in indeterminate x over a field F. The F[x] is vector space over F with respect to addition of two polynomials as addition of vectors and the product of a polynomial by a constant polynomial.
Q4) Suppose V(F) is a vector space and 0 be the zero vector of V. Then-
1. 
2. 
3. 
4. 
5. 
6. 
A4)
1. We have

We can write 
So that,

Now V is an abelian group with respect to addition.
So that by right cancellation law, we get-
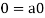
2. We have

We can write 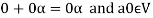
So that,
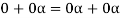
Now V is an abelian group with respect to addition.
So that by right cancellation law, we get-

3. We have 

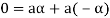
 is the additive inverse of
is the additive inverse of 

4. We have 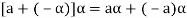


 is the additive inverse of
is the additive inverse of 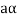
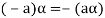
5. We have-

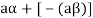
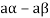
6. Suppose 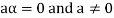 the inverse of ‘a’ exists because ‘a’ is non-zero element of the field.
the inverse of ‘a’ exists because ‘a’ is non-zero element of the field.

Again let-
 , then to prove
, then to prove 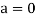 let
let 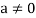 then inverse of ‘a’ exists
then inverse of ‘a’ exists
We get a contradiction that  must be a zero vector. Therefore ‘a’ must be equal to zero.
must be a zero vector. Therefore ‘a’ must be equal to zero.
So that
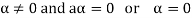
Q5) Define vector sub space.
A5)
Suppose V is a vector space over the field F and  . Then W is called subspace of V if W itself a vector space over F with respect to the operations of vector addition and scalar multiplication in V.
. Then W is called subspace of V if W itself a vector space over F with respect to the operations of vector addition and scalar multiplication in V.
Q6) The necessary and sufficient conditions for a non-empty sub-set W of a vector space V(F) to be a subspace of V are-
1. 
2. 
A6)
Necessary conditions-
W is an abelian group with respect to vector addition If W is a subspace of V.
So that 
Here W must be closed under a scalar multiplication so that the second condition is also necessary.
Sufficient conditions-
Let W is a non-empty subset of V satisfying the two given conditions.
From first condition-
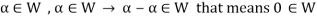
So that we can say that zero vector of V belongs to W. It is a zero vector of W as well.
Now 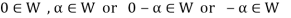
So that the additive inverse of each element of W is also in W.
So that-

Thus W is closed with respect to vector addition.
Q7) The intersection of any two subspaces  and
and  of a vector space V(F) is also a subspace of V(F). Prove.
of a vector space V(F) is also a subspace of V(F). Prove.
A7)
As we know that  therefore
therefore  is not empty.
is not empty.
Suppose 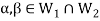 and
and 
Now, 
And 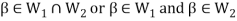
Since  is a subspace, therefore-
is a subspace, therefore-
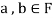 and
and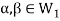 then
then 
Similarly, 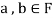
 then
then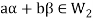
Now 
Thus,
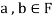 And
And 
Then 
So that 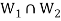 is a subspace of V(F).
is a subspace of V(F).
Q8) If 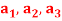 are fixed elements of a field F, then set of W of all ordered triads (
are fixed elements of a field F, then set of W of all ordered triads (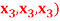 of elements of F,
of elements of F,
Such that-

Is a subspace of Prove.
Prove.
A8)
Suppose  are any two elements of W.
are any two elements of W.
Such that 
And these are the elements of F, such that-
 …………………….. (1)
…………………….. (1)
 ……………………. (2)
……………………. (2)
If a and b are two elements of F, we have

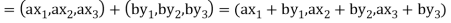
Now
= 
= 
= 

So that W is subspace of 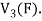
Q9) Let R be a field of real numbers. Now check whether which one of the following are subspaces of 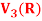
1. { 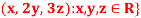
2. { 
3. { 
A9)
Suppose W = { 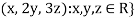
Let  be any two elements of W.
be any two elements of W.
If a and b are two real numbers, then-



Since  are real numbers.
are real numbers.
So that  and
and 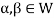 or
or 
So that W is a subspace of 
2. Let W = { 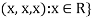
Let  be any two elements of W.
be any two elements of W.
If a and b are two real numbers, then-

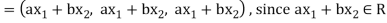
So that W is a subspace of 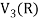
3. Let W ={
Now  is an element of W. Also
is an element of W. Also  is an element of R.
is an element of R.
But  which do not belong to W.
which do not belong to W.
Since  are not rational numbers.
are not rational numbers.
So that W is not closed under scalar multiplication.
W is not a subspace of 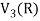
Q10) Define symmetric and skew-symmetric matrix.
A10)
The transpose  of an m × n matrix A is the n × m matrix obtained from A by interchanging the rows with the columns
of an m × n matrix A is the n × m matrix obtained from A by interchanging the rows with the columns
Suppose,
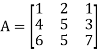
Then
Transpose of this matrix,
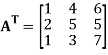
A symmetric matrix is a matrix A such that  = A.
= A.
A skew- symmetric matrix is a matrix A such that 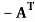 = A.
= A.
Q11) Any intersection of subspaces of a vector space V is a subspace of V. Prove.
A11)
Let C be a collection of subspaces of V, and let W denote the intersection of the subspaces in C. Since every subspace contains the zero vector, 0 ∈ W. Let a ∈ F and x, y ∈ W. Then x and y are contained in each subspace in C. Because each subspace in C is closed under addition and scalar multiplication, it follows that x+y and ax are contained in each subspace in C. Hence x+y and ax are also contained in W, so that W is a subspace of V
Q12) Define homomorphism.
A12)
Definition-
Suppose U(F) and V(F) are two vector spaces, then a mapping  is called a linear transformation of U into V, if:
is called a linear transformation of U into V, if:
1. 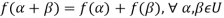
2. 
It is also called homomorphism.
Q13) What is kernel of a linear transformation.
A13)
Let f be a linear transformation of a vector space U(F) into a vector space V(F).
The kernel W of f is defined as-

The kernel W of f is a subset of U consisting of those elements of U which are mapped under f onto the zero vector V.
Since f(0) = 0, therefore atleast 0 belong to W. So that W is not empty.
Q14) The mapping  defined by-
defined by-

Is a linear transformation  .
.
What is the kernel of this linear transformation.
A14)
Let  be any two elements of
be any two elements of 
Let a, b be any two elements of F.
We have
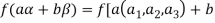 (
(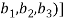
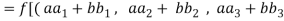

 =
= 

So that f is a linear transformation.
To show that f is onto  . Let
. Let  be any elements
be any elements  .
.
Then 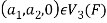 and we have
and we have 
So that f is onto 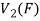
Therefore f is homomorphism of  onto
onto  .
.
If W is the kernel of this homomorphism then 
We have
∀
Also if  then
then 
Implies 
Therefore 
Hence W is the kernel of f.
Q15) Let V and W be vector spaces and T: V → W be linear. Then N(T) and R(T) are subspaces of V and W, respectively. Prove.
A15)
Here we will use the symbols 0 V and 0W to denote the zero vectors of V and W, respectively.
Since T(0 V) = 0W, we have that 0 V ∈ N(T). Let x, y ∈ N(T) and c ∈ F.
Then T(x + y) = T(x)+T(y) = 0W+0W = 0W, and T(c x) = c T(x) = c0W = 0W. Hence x + y ∈ N(T) and c x ∈ N(T), so that N(T) is a subspace of V. Because T(0 V) = 0W, we have that 0W ∈ R(T). Now let x, y ∈ R(T) and c ∈ F. Then there exist v and w in V such that T(v) = x and T(w) = y. So T(v + w) = T(v)+T(w) = x + y, and T(c v) = c T(v) = c x. Thus x+ y ∈ R(T) and c x ∈ R(T), so R(T) is a subspace of W.
Q16) Let A is a matrix of order m by n, then-

Prove.
A16)
If rank (A) = n, then the only solution to Ax = 0 is the trivial solution x = 0by using invertible matrix.
So that in this case null-space (A) = {0}, so nullity (A) = 0.
Now suppose rank (A) = r < n, in this case there are n – r > 0 free variable in the solution to Ax = 0.
Let  represent these free variables and let
represent these free variables and let  denote the solution obtained by sequentially setting each free variable to 1 and the remaining free variables to zero.
denote the solution obtained by sequentially setting each free variable to 1 and the remaining free variables to zero.
Here  is linearly independent.
is linearly independent.
Moreover every solution is to Ax = 0 is a linear combination of 

Which shows that 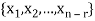 spans null-space (A).
spans null-space (A).
Thus  is a basis for null-space(A) and nullity (A) = n – r.
is a basis for null-space(A) and nullity (A) = n – r.
Q17) What is linear span?
A17)
Definition- Let V(F) be a vector space and S be a non-empty subset of V. Then the linear span of S is the set of all linear combinations of finite sets of elements of S and it is denoted by L(S). Thus we have-
L(S) = 

Q18) The linear span L(S) of any subset S of a vector space V(F) is s subspace of V generated by S. Prove.
A18)
Suppose  be any two elements of L(S).
be any two elements of L(S).
Then

And 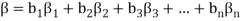
Where a and b are the elements of F and 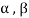 are the elements of S.
are the elements of S.
If a,b be any two elements of F, then-
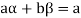 (
(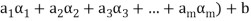 (
(
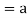 (
(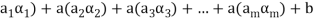 (
(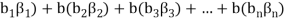

Thus  has been expressed as a linear combination of a finite set
has been expressed as a linear combination of a finite set  of the elements of S.
of the elements of S.
Consequently 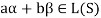
Thus,  and
and 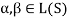 so that
so that 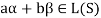
Hence L(S) is a subspace of V(F).
Q19) What is linear dependence and linear independence?
A19)
Linear dependence-
Let V(F) be a vector space.
A finite set 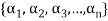 of vector of V is said to be linearly dependent if there exists scalars
of vector of V is said to be linearly dependent if there exists scalars  (not all of them as some of them might be zero)
(not all of them as some of them might be zero)
Such that-
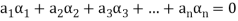
Linear independence-
Let V(F) be a vector space.
A finite set  of vector of V is said to be linearly independent if every relation if the form-
of vector of V is said to be linearly independent if every relation if the form-


Q20) Show that S = {(1 , 2 , 4) , (1 , 0 , 0) , (0 , 1 , 0) , (0 , 0 , 1)} is linearly dependent subset of the vector space  . Where R is the field of real numbers
. Where R is the field of real numbers
A20)
Here we have-
1 (1 , 2 , 4) + (-1) (1 , 0 , 0) + (-2) (0 ,1, 0) + (-4) (0, 0, 1)
= (1, 2 , 4) + (-1 , 0 , 0) + (0 ,-2, 0) + (0, 0, -4)
= (0, 0, 0)
That means it is a zero vector.
In this relation the scalar coefficients 1 , -1 , -2, -4 are all not zero.
So that we can conclude that S is linearly dependent.
Q21) If  are linearly independent vectors of V(F).where F is the field of complex numbers, then so also are
are linearly independent vectors of V(F).where F is the field of complex numbers, then so also are  . Prove.
. Prove.
A21)
Suppose a, b, c are scalars such that-

 …………….. (1)
…………….. (1)
But  are linearly independent vectors of V(F), so that equations (1) implies that-
are linearly independent vectors of V(F), so that equations (1) implies that-
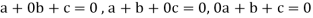
The coefficient matrix A of these equations will be-
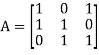
Here we get rank of A = 3, so that a = 0, b = 0, c = 0 is the only solution of the given equations, so that  are also linearly independent.
are also linearly independent.
Q22) State and prove extension theorem.
A22)
Statement-
Every linearly independent subset of a finitely generated vector space V(F) forms of a part of a basis of V.
Proof: Suppose  be a linearly independent subset of a finite dimensional vector space V(F) if dim V = n, then V has a finite basis, say
be a linearly independent subset of a finite dimensional vector space V(F) if dim V = n, then V has a finite basis, say 
Let us consider a set-
 …………. (1)
…………. (1)
Obviously L( , since there
, since there 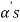 can be expressed as linear combination of
can be expressed as linear combination of  therefore the set
therefore the set 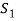 is linearly dependent.
is linearly dependent.
So that there is some vector of 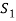 which is linear combination of its preceding vectors. This vector can not be any of the
which is linear combination of its preceding vectors. This vector can not be any of the 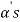 since the
since the  are linearly independent.
are linearly independent.
Therefore this vector must be some 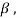 say
say 
Now omit the vector  from (1) and consider the set-
from (1) and consider the set-
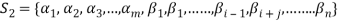
Obviously L( . If
. If  is linearly independent, then
is linearly independent, then 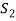 will be a basis of V and it is the required extended set which is a basis of V.
will be a basis of V and it is the required extended set which is a basis of V.
If  is not linearly independent, then repeating the above process a finite number of times. We shall get a linearly independent set containing
is not linearly independent, then repeating the above process a finite number of times. We shall get a linearly independent set containing  and spanning V. This set will be a basis of V contains the same number of elements, so that exactly n-m elements of the set of
and spanning V. This set will be a basis of V contains the same number of elements, so that exactly n-m elements of the set of  will be adjoined to S so as to form a basis of V.
will be adjoined to S so as to form a basis of V.
Q23) Show that the vectors (1, 2, 1), (2, 1, 0) and (1, -1, 2) form a basis of 
A23)
We know that set {(1,0,0) , (0,1,0) , (0,0,1)} forms a basis of 
So that dim 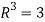 .
.
Now if we show that the set S = {(1, 2, 1), (2, 1, 0) , (1, -1, 2)} is linearly independent, then this set will form a basis of 
We have,
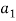 (1, 2, 1)+
(1, 2, 1)+ (2, 1, 0)+
(2, 1, 0)+ (1, -1, 2) = (0, 0, 0)
(1, -1, 2) = (0, 0, 0)
(
Which gives-

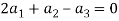
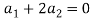
On solving these equations we get,

So we can say that the set S is linearly independent.
Therefore it forms a basis of 
Unit – 6
Vector space
Q1) Define vector space.
A1)
Let ‘F’ be any given field, then a given set V is said to be a vector space if-
1. There is a defined composition in ‘V’. This composition called addition of vectors which is denoted by ‘+’
2. There is a defined an external composition in ‘V’ over ‘F’. That will be denoted by scalar multiplication.
3. The two compositions satisfy the following conditions-
(a) 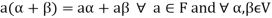
(b) 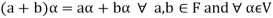
(c) 
(d) If 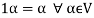 then 1 is the unity element of the field F.
then 1 is the unity element of the field F.
If V is a vector space over the field F, then we will denote vector space as V(F).
Q2) The set of all  matrices with their elements as real numbers is a vector space over the field F of real numbers with respect to addition of matrices as addition of vectors and multiplication of a matrix by a scalar as scalar multiplication.
matrices with their elements as real numbers is a vector space over the field F of real numbers with respect to addition of matrices as addition of vectors and multiplication of a matrix by a scalar as scalar multiplication.
A2)
V is an abelian group with respect to addition of matrices in groups.
The null matrix of m by n is the additive identity of this group.
If  then
then  as
as 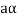 is also the matrix of m by n with elements of real numbers.
is also the matrix of m by n with elements of real numbers.
So that V is closed with respect to scalar multiplication.
We conclude that from matrices-
1. 
2. 
3. 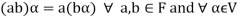
4.  Where 1 is the unity element of F.
Where 1 is the unity element of F.
Therefore we can say that V (F) is a vector space.
Q3) The vector space of all polynomials over a field F. Prove.
A3)
Suppose F[x] represents the set of all polynomials in indeterminate x over a field F. The F[x] is vector space over F with respect to addition of two polynomials as addition of vectors and the product of a polynomial by a constant polynomial.
Q4) Suppose V(F) is a vector space and 0 be the zero vector of V. Then-
1. 
2. 
3. 
4. 
5. 
6. 
A4)
1. We have
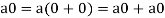
We can write 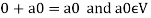
So that,

Now V is an abelian group with respect to addition.
So that by right cancellation law, we get-
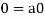
2. We have
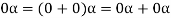
We can write 
So that,

Now V is an abelian group with respect to addition.
So that by right cancellation law, we get-

3. We have 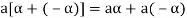

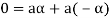
 is the additive inverse of
is the additive inverse of 

4. We have 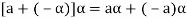


 is the additive inverse of
is the additive inverse of 

5. We have-



6. Suppose  the inverse of ‘a’ exists because ‘a’ is non-zero element of the field.
the inverse of ‘a’ exists because ‘a’ is non-zero element of the field.
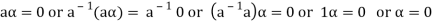
Again let-
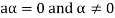 , then to prove
, then to prove  let
let  then inverse of ‘a’ exists
then inverse of ‘a’ exists
We get a contradiction that  must be a zero vector. Therefore ‘a’ must be equal to zero.
must be a zero vector. Therefore ‘a’ must be equal to zero.
So that

Q5) Define vector sub space.
A5)
Suppose V is a vector space over the field F and 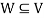 . Then W is called subspace of V if W itself a vector space over F with respect to the operations of vector addition and scalar multiplication in V.
. Then W is called subspace of V if W itself a vector space over F with respect to the operations of vector addition and scalar multiplication in V.
Q6) The necessary and sufficient conditions for a non-empty sub-set W of a vector space V(F) to be a subspace of V are-
1. 
2. 
A6)
Necessary conditions-
W is an abelian group with respect to vector addition If W is a subspace of V.
So that 
Here W must be closed under a scalar multiplication so that the second condition is also necessary.
Sufficient conditions-
Let W is a non-empty subset of V satisfying the two given conditions.
From first condition-

So that we can say that zero vector of V belongs to W. It is a zero vector of W as well.
Now 
So that the additive inverse of each element of W is also in W.
So that-

Thus W is closed with respect to vector addition.
Q7) The intersection of any two subspaces  and
and  of a vector space V(F) is also a subspace of V(F). Prove.
of a vector space V(F) is also a subspace of V(F). Prove.
A7)
As we know that 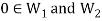 therefore
therefore  is not empty.
is not empty.
Suppose  and
and 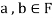
Now, 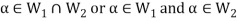
And 
Since 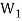 is a subspace, therefore-
is a subspace, therefore-
 and
and then
then 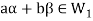
Similarly, 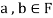
 then
then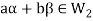
Now 
Thus,
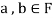 And
And 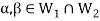
Then 
So that 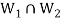 is a subspace of V(F).
is a subspace of V(F).
Q8) If 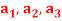 are fixed elements of a field F, then set of W of all ordered triads (
are fixed elements of a field F, then set of W of all ordered triads ( of elements of F,
of elements of F,
Such that-

Is a subspace of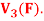 Prove.
Prove.
A8)
Suppose 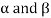 are any two elements of W.
are any two elements of W.
Such that 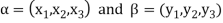
And these are the elements of F, such that-
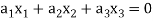 …………………….. (1)
…………………….. (1)
 ……………………. (2)
……………………. (2)
If a and b are two elements of F, we have


Now
= 
= 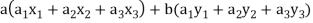
= 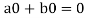

So that W is subspace of 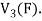
Q9) Let R be a field of real numbers. Now check whether which one of the following are subspaces of 
1. { 
2. { 
3. { 
A9)
Suppose W = { 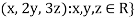
Let  be any two elements of W.
be any two elements of W.
If a and b are two real numbers, then-

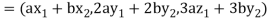

Since  are real numbers.
are real numbers.
So that  and
and 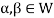 or
or 
So that W is a subspace of 
2. Let W = { 
Let  be any two elements of W.
be any two elements of W.
If a and b are two real numbers, then-
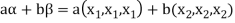

So that W is a subspace of 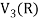
3. Let W ={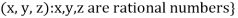
Now 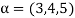 is an element of W. Also
is an element of W. Also  is an element of R.
is an element of R.
But 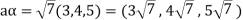 which do not belong to W.
which do not belong to W.
Since  are not rational numbers.
are not rational numbers.
So that W is not closed under scalar multiplication.
W is not a subspace of 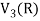
Q10) Define symmetric and skew-symmetric matrix.
A10)
The transpose 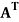 of an m × n matrix A is the n × m matrix obtained from A by interchanging the rows with the columns
of an m × n matrix A is the n × m matrix obtained from A by interchanging the rows with the columns
Suppose,

Then
Transpose of this matrix,

A symmetric matrix is a matrix A such that  = A.
= A.
A skew- symmetric matrix is a matrix A such that 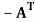 = A.
= A.
Q11) Any intersection of subspaces of a vector space V is a subspace of V. Prove.
A11)
Let C be a collection of subspaces of V, and let W denote the intersection of the subspaces in C. Since every subspace contains the zero vector, 0 ∈ W. Let a ∈ F and x, y ∈ W. Then x and y are contained in each subspace in C. Because each subspace in C is closed under addition and scalar multiplication, it follows that x+y and ax are contained in each subspace in C. Hence x+y and ax are also contained in W, so that W is a subspace of V
Q12) Define homomorphism.
A12)
Definition-
Suppose U(F) and V(F) are two vector spaces, then a mapping  is called a linear transformation of U into V, if:
is called a linear transformation of U into V, if:
1. 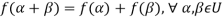
2. 
It is also called homomorphism.
Q13) What is kernel of a linear transformation.
A13)
Let f be a linear transformation of a vector space U(F) into a vector space V(F).
The kernel W of f is defined as-
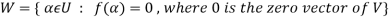
The kernel W of f is a subset of U consisting of those elements of U which are mapped under f onto the zero vector V.
Since f(0) = 0, therefore atleast 0 belong to W. So that W is not empty.
Q14) The mapping  defined by-
defined by-

Is a linear transformation  .
.
What is the kernel of this linear transformation.
A14)
Let  be any two elements of
be any two elements of 
Let a, b be any two elements of F.
We have
 (
(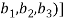


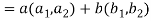 =
= 

So that f is a linear transformation.
To show that f is onto 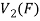 . Let
. Let  be any elements
be any elements 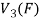 .
.
Then  and we have
and we have 
So that f is onto 
Therefore f is homomorphism of 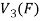 onto
onto 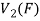 .
.
If W is the kernel of this homomorphism then 
We have
∀
Also if  then
then 
Implies 
Therefore 
Hence W is the kernel of f.
Q15) Let V and W be vector spaces and T: V → W be linear. Then N(T) and R(T) are subspaces of V and W, respectively. Prove.
A15)
Here we will use the symbols 0 V and 0W to denote the zero vectors of V and W, respectively.
Since T(0 V) = 0W, we have that 0 V ∈ N(T). Let x, y ∈ N(T) and c ∈ F.
Then T(x + y) = T(x)+T(y) = 0W+0W = 0W, and T(c x) = c T(x) = c0W = 0W. Hence x + y ∈ N(T) and c x ∈ N(T), so that N(T) is a subspace of V. Because T(0 V) = 0W, we have that 0W ∈ R(T). Now let x, y ∈ R(T) and c ∈ F. Then there exist v and w in V such that T(v) = x and T(w) = y. So T(v + w) = T(v)+T(w) = x + y, and T(c v) = c T(v) = c x. Thus x+ y ∈ R(T) and c x ∈ R(T), so R(T) is a subspace of W.
Q16) Let A is a matrix of order m by n, then-

Prove.
A16)
If rank (A) = n, then the only solution to Ax = 0 is the trivial solution x = 0by using invertible matrix.
So that in this case null-space (A) = {0}, so nullity (A) = 0.
Now suppose rank (A) = r < n, in this case there are n – r > 0 free variable in the solution to Ax = 0.
Let 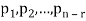 represent these free variables and let
represent these free variables and let  denote the solution obtained by sequentially setting each free variable to 1 and the remaining free variables to zero.
denote the solution obtained by sequentially setting each free variable to 1 and the remaining free variables to zero.
Here  is linearly independent.
is linearly independent.
Moreover every solution is to Ax = 0 is a linear combination of 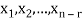

Which shows that 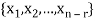 spans null-space (A).
spans null-space (A).
Thus  is a basis for null-space(A) and nullity (A) = n – r.
is a basis for null-space(A) and nullity (A) = n – r.
Q17) What is linear span?
A17)
Definition- Let V(F) be a vector space and S be a non-empty subset of V. Then the linear span of S is the set of all linear combinations of finite sets of elements of S and it is denoted by L(S). Thus we have-
L(S) = 

Q18) The linear span L(S) of any subset S of a vector space V(F) is s subspace of V generated by S. Prove.
A18)
Suppose  be any two elements of L(S).
be any two elements of L(S).
Then
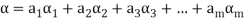
And 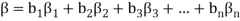
Where a and b are the elements of F and  are the elements of S.
are the elements of S.
If a,b be any two elements of F, then-
 (
( (
(
 (
(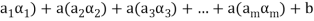 (
(

Thus  has been expressed as a linear combination of a finite set
has been expressed as a linear combination of a finite set  of the elements of S.
of the elements of S.
Consequently 
Thus,  and
and  so that
so that 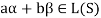
Hence L(S) is a subspace of V(F).
Q19) What is linear dependence and linear independence?
A19)
Linear dependence-
Let V(F) be a vector space.
A finite set 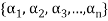 of vector of V is said to be linearly dependent if there exists scalars
of vector of V is said to be linearly dependent if there exists scalars 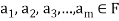 (not all of them as some of them might be zero)
(not all of them as some of them might be zero)
Such that-
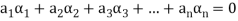
Linear independence-
Let V(F) be a vector space.
A finite set  of vector of V is said to be linearly independent if every relation if the form-
of vector of V is said to be linearly independent if every relation if the form-


Q20) Show that S = {(1 , 2 , 4) , (1 , 0 , 0) , (0 , 1 , 0) , (0 , 0 , 1)} is linearly dependent subset of the vector space  . Where R is the field of real numbers
. Where R is the field of real numbers
A20)
Here we have-
1 (1 , 2 , 4) + (-1) (1 , 0 , 0) + (-2) (0 ,1, 0) + (-4) (0, 0, 1)
= (1, 2 , 4) + (-1 , 0 , 0) + (0 ,-2, 0) + (0, 0, -4)
= (0, 0, 0)
That means it is a zero vector.
In this relation the scalar coefficients 1 , -1 , -2, -4 are all not zero.
So that we can conclude that S is linearly dependent.
Q21) If 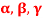 are linearly independent vectors of V(F).where F is the field of complex numbers, then so also are
are linearly independent vectors of V(F).where F is the field of complex numbers, then so also are  . Prove.
. Prove.
A21)
Suppose a, b, c are scalars such that-

 …………….. (1)
…………….. (1)
But  are linearly independent vectors of V(F), so that equations (1) implies that-
are linearly independent vectors of V(F), so that equations (1) implies that-

The coefficient matrix A of these equations will be-

Here we get rank of A = 3, so that a = 0, b = 0, c = 0 is the only solution of the given equations, so that  are also linearly independent.
are also linearly independent.
Q22) State and prove extension theorem.
A22)
Statement-
Every linearly independent subset of a finitely generated vector space V(F) forms of a part of a basis of V.
Proof: Suppose  be a linearly independent subset of a finite dimensional vector space V(F) if dim V = n, then V has a finite basis, say
be a linearly independent subset of a finite dimensional vector space V(F) if dim V = n, then V has a finite basis, say 
Let us consider a set-
 …………. (1)
…………. (1)
Obviously L( , since there
, since there 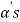 can be expressed as linear combination of
can be expressed as linear combination of 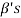 therefore the set
therefore the set 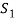 is linearly dependent.
is linearly dependent.
So that there is some vector of 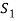 which is linear combination of its preceding vectors. This vector can not be any of the
which is linear combination of its preceding vectors. This vector can not be any of the 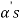 since the
since the  are linearly independent.
are linearly independent.
Therefore this vector must be some  say
say 
Now omit the vector  from (1) and consider the set-
from (1) and consider the set-

Obviously L( . If
. If  is linearly independent, then
is linearly independent, then  will be a basis of V and it is the required extended set which is a basis of V.
will be a basis of V and it is the required extended set which is a basis of V.
If  is not linearly independent, then repeating the above process a finite number of times. We shall get a linearly independent set containing
is not linearly independent, then repeating the above process a finite number of times. We shall get a linearly independent set containing  and spanning V. This set will be a basis of V contains the same number of elements, so that exactly n-m elements of the set of
and spanning V. This set will be a basis of V contains the same number of elements, so that exactly n-m elements of the set of  will be adjoined to S so as to form a basis of V.
will be adjoined to S so as to form a basis of V.
Q23) Show that the vectors (1, 2, 1), (2, 1, 0) and (1, -1, 2) form a basis of 
A23)
We know that set {(1,0,0) , (0,1,0) , (0,0,1)} forms a basis of 
So that dim 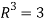 .
.
Now if we show that the set S = {(1, 2, 1), (2, 1, 0) , (1, -1, 2)} is linearly independent, then this set will form a basis of 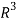
We have,
 (1, 2, 1)+
(1, 2, 1)+ (2, 1, 0)+
(2, 1, 0)+ (1, -1, 2) = (0, 0, 0)
(1, -1, 2) = (0, 0, 0)
(
Which gives-

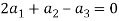

On solving these equations we get,

So we can say that the set S is linearly independent.
Therefore it forms a basis of 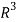
Unit – 6
Unit – 6
Unit – 6
Unit – 6
Unit – 6
Unit – 6
Vector space
Q1) Define vector space.
A1)
Let ‘F’ be any given field, then a given set V is said to be a vector space if-
1. There is a defined composition in ‘V’. This composition called addition of vectors which is denoted by ‘+’
2. There is a defined an external composition in ‘V’ over ‘F’. That will be denoted by scalar multiplication.
3. The two compositions satisfy the following conditions-
(a) 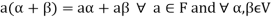
(b) 
(c) 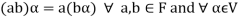
(d) If  then 1 is the unity element of the field F.
then 1 is the unity element of the field F.
If V is a vector space over the field F, then we will denote vector space as V(F).
Q2) The set of all  matrices with their elements as real numbers is a vector space over the field F of real numbers with respect to addition of matrices as addition of vectors and multiplication of a matrix by a scalar as scalar multiplication.
matrices with their elements as real numbers is a vector space over the field F of real numbers with respect to addition of matrices as addition of vectors and multiplication of a matrix by a scalar as scalar multiplication.
A2)
V is an abelian group with respect to addition of matrices in groups.
The null matrix of m by n is the additive identity of this group.
If  then
then  as
as 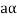 is also the matrix of m by n with elements of real numbers.
is also the matrix of m by n with elements of real numbers.
So that V is closed with respect to scalar multiplication.
We conclude that from matrices-
1. 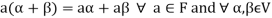
2. 
3. 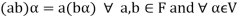
4.  Where 1 is the unity element of F.
Where 1 is the unity element of F.
Therefore we can say that V (F) is a vector space.
Q3) The vector space of all polynomials over a field F. Prove.
A3)
Suppose F[x] represents the set of all polynomials in indeterminate x over a field F. The F[x] is vector space over F with respect to addition of two polynomials as addition of vectors and the product of a polynomial by a constant polynomial.
Q4) Suppose V(F) is a vector space and 0 be the zero vector of V. Then-
1. 
2. 
3. 
4. 
5. 
6. 
A4)
1. We have
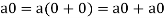
We can write 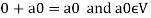
So that,

Now V is an abelian group with respect to addition.
So that by right cancellation law, we get-

2. We have

We can write 
So that,
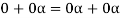
Now V is an abelian group with respect to addition.
So that by right cancellation law, we get-

3. We have 


 is the additive inverse of
is the additive inverse of 

4. We have 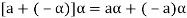
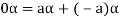

 is the additive inverse of
is the additive inverse of 
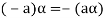
5. We have-


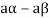
6. Suppose 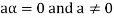 the inverse of ‘a’ exists because ‘a’ is non-zero element of the field.
the inverse of ‘a’ exists because ‘a’ is non-zero element of the field.
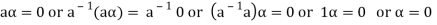
Again let-
 , then to prove
, then to prove  let
let  then inverse of ‘a’ exists
then inverse of ‘a’ exists
We get a contradiction that  must be a zero vector. Therefore ‘a’ must be equal to zero.
must be a zero vector. Therefore ‘a’ must be equal to zero.
So that

Q5) Define vector sub space.
A5)
Suppose V is a vector space over the field F and  . Then W is called subspace of V if W itself a vector space over F with respect to the operations of vector addition and scalar multiplication in V.
. Then W is called subspace of V if W itself a vector space over F with respect to the operations of vector addition and scalar multiplication in V.
Q6) The necessary and sufficient conditions for a non-empty sub-set W of a vector space V(F) to be a subspace of V are-
1. 
2. 
A6)
Necessary conditions-
W is an abelian group with respect to vector addition If W is a subspace of V.
So that 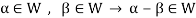
Here W must be closed under a scalar multiplication so that the second condition is also necessary.
Sufficient conditions-
Let W is a non-empty subset of V satisfying the two given conditions.
From first condition-
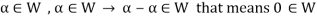
So that we can say that zero vector of V belongs to W. It is a zero vector of W as well.
Now 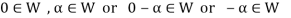
So that the additive inverse of each element of W is also in W.
So that-

Thus W is closed with respect to vector addition.
Q7) The intersection of any two subspaces  and
and  of a vector space V(F) is also a subspace of V(F). Prove.
of a vector space V(F) is also a subspace of V(F). Prove.
A7)
As we know that 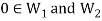 therefore
therefore  is not empty.
is not empty.
Suppose  and
and 
Now, 
And 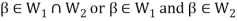
Since  is a subspace, therefore-
is a subspace, therefore-
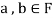 and
and then
then 
Similarly, 
 then
then
Now 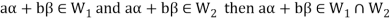
Thus,
 And
And 
Then 
So that  is a subspace of V(F).
is a subspace of V(F).
Q8) If  are fixed elements of a field F, then set of W of all ordered triads (
are fixed elements of a field F, then set of W of all ordered triads ( of elements of F,
of elements of F,
Such that-

Is a subspace of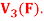 Prove.
Prove.
A8)
Suppose 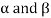 are any two elements of W.
are any two elements of W.
Such that 
And these are the elements of F, such that-
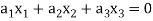 …………………….. (1)
…………………….. (1)
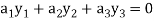 ……………………. (2)
……………………. (2)
If a and b are two elements of F, we have
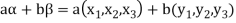

Now
= 
= 
= 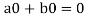

So that W is subspace of 
Q9) Let R be a field of real numbers. Now check whether which one of the following are subspaces of 
1. { 
2. { 
3. { 
A9)
Suppose W = { 
Let  be any two elements of W.
be any two elements of W.
If a and b are two real numbers, then-


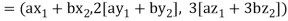
Since  are real numbers.
are real numbers.
So that  and
and  or
or 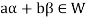
So that W is a subspace of 
2. Let W = { 
Let  be any two elements of W.
be any two elements of W.
If a and b are two real numbers, then-
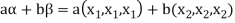

So that W is a subspace of 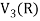
3. Let W ={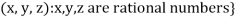
Now 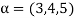 is an element of W. Also
is an element of W. Also  is an element of R.
is an element of R.
But  which do not belong to W.
which do not belong to W.
Since  are not rational numbers.
are not rational numbers.
So that W is not closed under scalar multiplication.
W is not a subspace of 
Q10) Define symmetric and skew-symmetric matrix.
A10)
The transpose 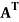 of an m × n matrix A is the n × m matrix obtained from A by interchanging the rows with the columns
of an m × n matrix A is the n × m matrix obtained from A by interchanging the rows with the columns
Suppose,

Then
Transpose of this matrix,

A symmetric matrix is a matrix A such that 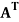 = A.
= A.
A skew- symmetric matrix is a matrix A such that  = A.
= A.
Q11) Any intersection of subspaces of a vector space V is a subspace of V. Prove.
A11)
Let C be a collection of subspaces of V, and let W denote the intersection of the subspaces in C. Since every subspace contains the zero vector, 0 ∈ W. Let a ∈ F and x, y ∈ W. Then x and y are contained in each subspace in C. Because each subspace in C is closed under addition and scalar multiplication, it follows that x+y and ax are contained in each subspace in C. Hence x+y and ax are also contained in W, so that W is a subspace of V
Q12) Define homomorphism.
A12)
Definition-
Suppose U(F) and V(F) are two vector spaces, then a mapping 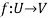 is called a linear transformation of U into V, if:
is called a linear transformation of U into V, if:
1. 
2. 
It is also called homomorphism.
Q13) What is kernel of a linear transformation.
A13)
Let f be a linear transformation of a vector space U(F) into a vector space V(F).
The kernel W of f is defined as-

The kernel W of f is a subset of U consisting of those elements of U which are mapped under f onto the zero vector V.
Since f(0) = 0, therefore atleast 0 belong to W. So that W is not empty.
Q14) The mapping  defined by-
defined by-

Is a linear transformation  .
.
What is the kernel of this linear transformation.
A14)
Let  be any two elements of
be any two elements of 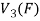
Let a, b be any two elements of F.
We have
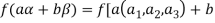 (
(
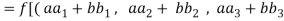

 =
= 

So that f is a linear transformation.
To show that f is onto 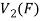 . Let
. Let  be any elements
be any elements  .
.
Then 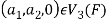 and we have
and we have 
So that f is onto 
Therefore f is homomorphism of 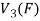 onto
onto  .
.
If W is the kernel of this homomorphism then 
We have
∀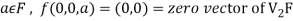
Also if  then
then 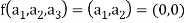
Implies 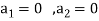
Therefore 
Hence W is the kernel of f.
Q15) Let V and W be vector spaces and T: V → W be linear. Then N(T) and R(T) are subspaces of V and W, respectively. Prove.
A15)
Here we will use the symbols 0 V and 0W to denote the zero vectors of V and W, respectively.
Since T(0 V) = 0W, we have that 0 V ∈ N(T). Let x, y ∈ N(T) and c ∈ F.
Then T(x + y) = T(x)+T(y) = 0W+0W = 0W, and T(c x) = c T(x) = c0W = 0W. Hence x + y ∈ N(T) and c x ∈ N(T), so that N(T) is a subspace of V. Because T(0 V) = 0W, we have that 0W ∈ R(T). Now let x, y ∈ R(T) and c ∈ F. Then there exist v and w in V such that T(v) = x and T(w) = y. So T(v + w) = T(v)+T(w) = x + y, and T(c v) = c T(v) = c x. Thus x+ y ∈ R(T) and c x ∈ R(T), so R(T) is a subspace of W.
Q16) Let A is a matrix of order m by n, then-

Prove.
A16)
If rank (A) = n, then the only solution to Ax = 0 is the trivial solution x = 0by using invertible matrix.
So that in this case null-space (A) = {0}, so nullity (A) = 0.
Now suppose rank (A) = r < n, in this case there are n – r > 0 free variable in the solution to Ax = 0.
Let 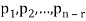 represent these free variables and let
represent these free variables and let  denote the solution obtained by sequentially setting each free variable to 1 and the remaining free variables to zero.
denote the solution obtained by sequentially setting each free variable to 1 and the remaining free variables to zero.
Here  is linearly independent.
is linearly independent.
Moreover every solution is to Ax = 0 is a linear combination of 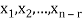
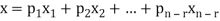
Which shows that  spans null-space (A).
spans null-space (A).
Thus  is a basis for null-space(A) and nullity (A) = n – r.
is a basis for null-space(A) and nullity (A) = n – r.
Q17) What is linear span?
A17)
Definition- Let V(F) be a vector space and S be a non-empty subset of V. Then the linear span of S is the set of all linear combinations of finite sets of elements of S and it is denoted by L(S). Thus we have-
L(S) = 

Q18) The linear span L(S) of any subset S of a vector space V(F) is s subspace of V generated by S. Prove.
A18)
Suppose  be any two elements of L(S).
be any two elements of L(S).
Then

And 
Where a and b are the elements of F and  are the elements of S.
are the elements of S.
If a,b be any two elements of F, then-
 (
( (
(
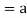 (
( (
(
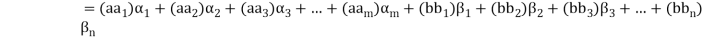
Thus  has been expressed as a linear combination of a finite set
has been expressed as a linear combination of a finite set  of the elements of S.
of the elements of S.
Consequently 
Thus,  and
and  so that
so that 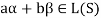
Hence L(S) is a subspace of V(F).
Q19) What is linear dependence and linear independence?
A19)
Linear dependence-
Let V(F) be a vector space.
A finite set  of vector of V is said to be linearly dependent if there exists scalars
of vector of V is said to be linearly dependent if there exists scalars 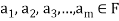 (not all of them as some of them might be zero)
(not all of them as some of them might be zero)
Such that-

Linear independence-
Let V(F) be a vector space.
A finite set  of vector of V is said to be linearly independent if every relation if the form-
of vector of V is said to be linearly independent if every relation if the form-

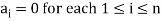
Q20) Show that S = {(1 , 2 , 4) , (1 , 0 , 0) , (0 , 1 , 0) , (0 , 0 , 1)} is linearly dependent subset of the vector space  . Where R is the field of real numbers
. Where R is the field of real numbers
A20)
Here we have-
1 (1 , 2 , 4) + (-1) (1 , 0 , 0) + (-2) (0 ,1, 0) + (-4) (0, 0, 1)
= (1, 2 , 4) + (-1 , 0 , 0) + (0 ,-2, 0) + (0, 0, -4)
= (0, 0, 0)
That means it is a zero vector.
In this relation the scalar coefficients 1 , -1 , -2, -4 are all not zero.
So that we can conclude that S is linearly dependent.
Q21) If 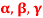 are linearly independent vectors of V(F).where F is the field of complex numbers, then so also are
are linearly independent vectors of V(F).where F is the field of complex numbers, then so also are  . Prove.
. Prove.
A21)
Suppose a, b, c are scalars such that-

 …………….. (1)
…………….. (1)
But 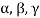 are linearly independent vectors of V(F), so that equations (1) implies that-
are linearly independent vectors of V(F), so that equations (1) implies that-

The coefficient matrix A of these equations will be-
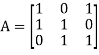
Here we get rank of A = 3, so that a = 0, b = 0, c = 0 is the only solution of the given equations, so that 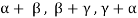 are also linearly independent.
are also linearly independent.
Q22) State and prove extension theorem.
A22)
Statement-
Every linearly independent subset of a finitely generated vector space V(F) forms of a part of a basis of V.
Proof: Suppose  be a linearly independent subset of a finite dimensional vector space V(F) if dim V = n, then V has a finite basis, say
be a linearly independent subset of a finite dimensional vector space V(F) if dim V = n, then V has a finite basis, say 
Let us consider a set-
 …………. (1)
…………. (1)
Obviously L( , since there
, since there 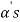 can be expressed as linear combination of
can be expressed as linear combination of 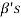 therefore the set
therefore the set  is linearly dependent.
is linearly dependent.
So that there is some vector of 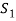 which is linear combination of its preceding vectors. This vector can not be any of the
which is linear combination of its preceding vectors. This vector can not be any of the  since the
since the  are linearly independent.
are linearly independent.
Therefore this vector must be some  say
say 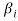
Now omit the vector 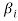 from (1) and consider the set-
from (1) and consider the set-

Obviously L( . If
. If 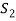 is linearly independent, then
is linearly independent, then  will be a basis of V and it is the required extended set which is a basis of V.
will be a basis of V and it is the required extended set which is a basis of V.
If  is not linearly independent, then repeating the above process a finite number of times. We shall get a linearly independent set containing
is not linearly independent, then repeating the above process a finite number of times. We shall get a linearly independent set containing  and spanning V. This set will be a basis of V contains the same number of elements, so that exactly n-m elements of the set of
and spanning V. This set will be a basis of V contains the same number of elements, so that exactly n-m elements of the set of 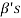 will be adjoined to S so as to form a basis of V.
will be adjoined to S so as to form a basis of V.
Q23) Show that the vectors (1, 2, 1), (2, 1, 0) and (1, -1, 2) form a basis of 
A23)
We know that set {(1,0,0) , (0,1,0) , (0,0,1)} forms a basis of 
So that dim  .
.
Now if we show that the set S = {(1, 2, 1), (2, 1, 0) , (1, -1, 2)} is linearly independent, then this set will form a basis of 
We have,
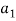 (1, 2, 1)+
(1, 2, 1)+ (2, 1, 0)+
(2, 1, 0)+ (1, -1, 2) = (0, 0, 0)
(1, -1, 2) = (0, 0, 0)
(
Which gives-



On solving these equations we get,
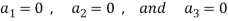
So we can say that the set S is linearly independent.
Therefore it forms a basis of