Unit – 8
Inner product and Orthogonality
Q1) What is the norm of a vector?
A1)
By the third axiom of an inner product, <u, v> is nonnegative for any vector u. Thus, its positive square root exists. We use the notation

This nonnegative number is called the norm or length of u. The relation ||u||2 = <u, u> will be used frequently.
If ||u|| = 1 or, equivalently, if <u, u> = 1, then u is called a unit vector and it is said to be normalized. Every nonzero vector v in V can be multiplied by the reciprocal of its length to obtain the unit vector

Which is a positive multiple of v. This process is called normalizing v.
Q2) What is orthogonality?
A2)
Let V be an inner product space. The vectors u, v  V are said to be orthogonal and u is said to be orthogonal to v if
V are said to be orthogonal and u is said to be orthogonal to v if
<u, v> = 0
The relation is clearly symmetric—if u is orthogonal to v, then <v, u> = 0, and so v is orthogonal to u. We note that 0  V is orthogonal to every v
V is orthogonal to every v  V, because
V, because
Conversely, if u is orthogonal to every v 2 V, then <u, u> = 0 and hence u = 0 by third axiom: Observe that u and v are orthogonal if and only if cos y = 0, where y is the angle between u and v. Also, this is true if and only if u and v are ‘‘perpendicular’’—that is, y = 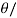 2 (or y = 90degree).
2 (or y = 90degree).
Q3) What is symmetric matrix?
A3)
In linear algebra, a symmetric matrix is a square matrix that is equal to its transpose. Formally, because equal matrices have equal dimensions, only square matrices can be symmetric. The entries of a symmetric matrix are symmetric with respect to the main diagonal. So, if aᵢⱼ denotes the entry in the i-th row and j-th column then for all indices i and j. Every square diagonal matrix is symmetric, since all off-diagonal elements are zero.
Any square matrix is said to be symmetric matrix if its transpose equals to the matrix itself.
For example:
 &
& 
Q4) Check whether the following matrix A is symmetric or not?
A = 
A4)
As we know that if the transpose of the given matrix is same as the matrix itself then the matrix is called symmetric matrix.
So that, first we will find its transpose,
Transpose of matrix A ,

Here,
A = 
So that, the matrix A is symmetric.
Q5) Show that any square matrix can be expressed as the sum of symmetric matrix and anti- symmetric matrix.
A5)
Suppose A is any square matrix
Then,
A = 
Now,
(A + A’)’ = A’ + A
A+A’ is a symmetric matrix.
Also,
(A - A’)’ = A’ – A
Here A’ – A is an anti – symmetric matrix
So that,
Square matrix = symmetric matrix + anti-symmetric matrix
Q6) Let A be a real symmetric matrix whose diagonal entries are all positive real numbers. Prove.
A6)
Is this true for all of the diagonal entries of the inverse matrix A-1 are also positive? If so, prove it. Otherwise give a counter example
Solution: The statement is false, hence we give a counter example
Let us consider the following 2 2 matrix
2 matrix
A = 
The matrix A satisfies the required conditions, that is A is symmetric and its diagonal entries are positive.
The determinant det(A) = (1)(1)-(2)(2) = -3 and the inverse of A is given by
A-1=  =
= 
By the formula for the inverse matrix for 2 2 matrices.
2 matrices.
This shows that the diagonal entries of the inverse matric A-1 are negative.
Q7) Let A and B be n n skew-matrices. Namely AT = -A and BT = -B
n skew-matrices. Namely AT = -A and BT = -B
(a) Prove that A+B is skew-symmetric.
(b) Prove that cA is skew-symmetric for any scalar c.
(c) Let P be an m n matrix. Prove that PTAP is skew-symmetric.
n matrix. Prove that PTAP is skew-symmetric.
A7)
(a) (A+B)T = AT + BT = (-A) +(-B) = -(A+B)
Hence A+B is skew symmetric.
(b) (cA)T = c.AT =c(-A) = -cA
Thus, cA is skew-symmetric.
(c)Let P be an m n matrix. Prove that PT AP is skew-symmetric.
n matrix. Prove that PT AP is skew-symmetric.
Using the properties, we get,
(PT AP)T = PTAT(PT)T = PTATp
= PT (-A) P = - (PT AP)
Thus (PT AP) is skew-symmetric.
Q8) What is quadratic form?
A8)
Quadratic form can be expressed as a product of matrices.
Q(x) = X’ AX,
Where,
X =  and A =
and A = 
X’ is the transpose of X,
X’AX = [ x1 x2 x3] 
= [ a11x1 + a21x2 + a31x3 a12x1 + a22x2 + a32x3 a13x1 + a23x2 + a33x3]
= a11x12 + a21x1x2 + a31 x1x3 + a12x1x2 + a22x22 +a32x2x3 + a13x1x3 + a23x2x3 + a33x32
= a11x12 + a22x22+a33x32+(a12+a21)x1x2 + (a23+ a32)x2x+(a31+ a13)x1x3
Which is the quadratic form.
Q9) Find the real matrix of the following quadratic form:
Q(x1, x2, x3) = x2 + 4x22 + 6x32 + 2x1x2 + x2x3 + 3x1x3
A9)
Here we will compare the coefficients with the standard quadratic equation,
We get,
a11 = 1, a22 = 4, a33 = 6, a12 = 2, a21 = 0, a23 = 1, a32 = 0, a13 = 3, a31 = 0
Q(x1, x2, x3) = [x1 x2 x3] = [ x1 2x1+4x2 3x1 + x2+ 6x3]
= [ x1 2x1+4x2 3x1 + x2+ 6x3] 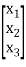
= x12 + 2x1x2 + 4x22 + 3x1x3 + x2x3 + 6x32
Q10) What is inner product?
A10)
Let V be a vector space over F. An inner product on V is a function that assigns, to every ordered pair of vectors x and y in V, a scalar in F, denoted  , such that for all x, y, and z in V and all c in F, the following hold:
, such that for all x, y, and z in V and all c in F, the following hold:
(a) 
(b) 
(c) 
(d) 
Note that (c) reduces to =
=  if F = R. Conditions (a) and (b) simply require that the inner product be linear in the first component.
if F = R. Conditions (a) and (b) simply require that the inner product be linear in the first component.
It is easily shown that if  and
and  , then
, then

Q11) What is an inner product space?
A11)
A vector space V over F endowed with a specific inner product is called an inner product space. If F = C, we call V a complex inner product It is clear that if V has an inner product 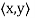 and W is a subspace of
and W is a subspace of
V, then W is also an inner product space when the same function  is
is
Restricted to the vectors x, y ∈ W.space, whereas if F = R, we call V a real inner product space.
Q12) What is Gram- Schmidt orthogonalization process?
A12)
Suppose {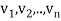 } is a basis of an inner product space V. One can use this basis to construct an orthogonal basis {
} is a basis of an inner product space V. One can use this basis to construct an orthogonal basis {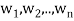 } of V as follows. Set
} of V as follows. Set



………………
……………….
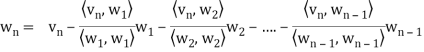
In other words, for k = 2, 3, . . . , n, we define

Where

Is the component of  .
.
Each  is orthogonal to the preceeding w’s. Thus,
is orthogonal to the preceeding w’s. Thus, form an orthogonal basis for V as claimed. Normalizing each wi will then yield an orthonormal basis for V.
form an orthogonal basis for V as claimed. Normalizing each wi will then yield an orthonormal basis for V.
The above process is known as the Gram–Schmidt orthogonalization process.
Q13) Apply the Gram–Schmidt orthogonalization process to find an orthogonal basis and then an orthonormal basis for the subspace U of  spanned by
spanned by

A13)
Step-1: First  =
= 
Step-2: Compute
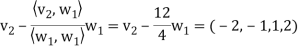
Now set- 
Step-3: Compute

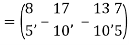
Clear fractions to obtain, 
Thus,  ,
,  ,
,  form an orthogonal basis for U. Normalize these vectors to obtain an orthonormal basis
form an orthogonal basis for U. Normalize these vectors to obtain an orthonormal basis
 of U. We have
of U. We have



So

Q14) Find the orthogonal canonical form of the quadratic form.
5
A14)
The matrix form of this quadratic equation can be written as,
A = 
We can find the eigen values of A as –
|A -  | = 0
| = 0
 = 0
= 0
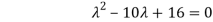
Which gives,

The required orthogonal canonical reduction will be,
8 .
.
Q15) What is the diagonalization of linear operators?
A15)
Consider a linear operator T: V  V. Then T is said to be diagonalizable if it can be represented by a diagonal matrix D. Thus, T is diagonalizable if and only if there exists a basis S = {
V. Then T is said to be diagonalizable if it can be represented by a diagonal matrix D. Thus, T is diagonalizable if and only if there exists a basis S = { } of V for which
} of V for which


………………
……………….

In such a case, T is represented by the diagonal matrix
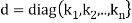
Relative to the basis S.
Unit – 8
Inner product and Orthogonality
Q1) What is the norm of a vector?
A1)
By the third axiom of an inner product, <u, v> is nonnegative for any vector u. Thus, its positive square root exists. We use the notation

This nonnegative number is called the norm or length of u. The relation ||u||2 = <u, u> will be used frequently.
If ||u|| = 1 or, equivalently, if <u, u> = 1, then u is called a unit vector and it is said to be normalized. Every nonzero vector v in V can be multiplied by the reciprocal of its length to obtain the unit vector

Which is a positive multiple of v. This process is called normalizing v.
Q2) What is orthogonality?
A2)
Let V be an inner product space. The vectors u, v  V are said to be orthogonal and u is said to be orthogonal to v if
V are said to be orthogonal and u is said to be orthogonal to v if
<u, v> = 0
The relation is clearly symmetric—if u is orthogonal to v, then <v, u> = 0, and so v is orthogonal to u. We note that 0  V is orthogonal to every v
V is orthogonal to every v  V, because
V, because
Conversely, if u is orthogonal to every v 2 V, then <u, u> = 0 and hence u = 0 by third axiom: Observe that u and v are orthogonal if and only if cos y = 0, where y is the angle between u and v. Also, this is true if and only if u and v are ‘‘perpendicular’’—that is, y =  2 (or y = 90degree).
2 (or y = 90degree).
Q3) What is symmetric matrix?
A3)
In linear algebra, a symmetric matrix is a square matrix that is equal to its transpose. Formally, because equal matrices have equal dimensions, only square matrices can be symmetric. The entries of a symmetric matrix are symmetric with respect to the main diagonal. So, if aᵢⱼ denotes the entry in the i-th row and j-th column then for all indices i and j. Every square diagonal matrix is symmetric, since all off-diagonal elements are zero.
Any square matrix is said to be symmetric matrix if its transpose equals to the matrix itself.
For example:
 &
& 
Q4) Check whether the following matrix A is symmetric or not?
A = 
A4)
As we know that if the transpose of the given matrix is same as the matrix itself then the matrix is called symmetric matrix.
So that, first we will find its transpose,
Transpose of matrix A ,

Here,
A = 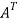
So that, the matrix A is symmetric.
Q5) Show that any square matrix can be expressed as the sum of symmetric matrix and anti- symmetric matrix.
A5)
Suppose A is any square matrix
Then,
A = 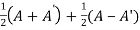
Now,
(A + A’)’ = A’ + A
A+A’ is a symmetric matrix.
Also,
(A - A’)’ = A’ – A
Here A’ – A is an anti – symmetric matrix
So that,
Square matrix = symmetric matrix + anti-symmetric matrix
Q6) Let A be a real symmetric matrix whose diagonal entries are all positive real numbers. Prove.
A6)
Is this true for all of the diagonal entries of the inverse matrix A-1 are also positive? If so, prove it. Otherwise give a counter example
Solution: The statement is false, hence we give a counter example
Let us consider the following 2 2 matrix
2 matrix
A = 
The matrix A satisfies the required conditions, that is A is symmetric and its diagonal entries are positive.
The determinant det(A) = (1)(1)-(2)(2) = -3 and the inverse of A is given by
A-1=  =
= 
By the formula for the inverse matrix for 2 2 matrices.
2 matrices.
This shows that the diagonal entries of the inverse matric A-1 are negative.
Q7) Let A and B be n n skew-matrices. Namely AT = -A and BT = -B
n skew-matrices. Namely AT = -A and BT = -B
(a) Prove that A+B is skew-symmetric.
(b) Prove that cA is skew-symmetric for any scalar c.
(c) Let P be an m n matrix. Prove that PTAP is skew-symmetric.
n matrix. Prove that PTAP is skew-symmetric.
A7)
(a) (A+B)T = AT + BT = (-A) +(-B) = -(A+B)
Hence A+B is skew symmetric.
(b) (cA)T = c.AT =c(-A) = -cA
Thus, cA is skew-symmetric.
(c)Let P be an m n matrix. Prove that PT AP is skew-symmetric.
n matrix. Prove that PT AP is skew-symmetric.
Using the properties, we get,
(PT AP)T = PTAT(PT)T = PTATp
= PT (-A) P = - (PT AP)
Thus (PT AP) is skew-symmetric.
Q8) What is quadratic form?
A8)
Quadratic form can be expressed as a product of matrices.
Q(x) = X’ AX,
Where,
X =  and A =
and A = 
X’ is the transpose of X,
X’AX = [ x1 x2 x3] 
= [ a11x1 + a21x2 + a31x3 a12x1 + a22x2 + a32x3 a13x1 + a23x2 + a33x3]
= a11x12 + a21x1x2 + a31 x1x3 + a12x1x2 + a22x22 +a32x2x3 + a13x1x3 + a23x2x3 + a33x32
= a11x12 + a22x22+a33x32+(a12+a21)x1x2 + (a23+ a32)x2x+(a31+ a13)x1x3
Which is the quadratic form.
Q9) Find the real matrix of the following quadratic form:
Q(x1, x2, x3) = x2 + 4x22 + 6x32 + 2x1x2 + x2x3 + 3x1x3
A9)
Here we will compare the coefficients with the standard quadratic equation,
We get,
a11 = 1, a22 = 4, a33 = 6, a12 = 2, a21 = 0, a23 = 1, a32 = 0, a13 = 3, a31 = 0
Q(x1, x2, x3) = [x1 x2 x3] = [ x1 2x1+4x2 3x1 + x2+ 6x3]
= [ x1 2x1+4x2 3x1 + x2+ 6x3] 
= x12 + 2x1x2 + 4x22 + 3x1x3 + x2x3 + 6x32
Q10) What is inner product?
A10)
Let V be a vector space over F. An inner product on V is a function that assigns, to every ordered pair of vectors x and y in V, a scalar in F, denoted 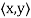 , such that for all x, y, and z in V and all c in F, the following hold:
, such that for all x, y, and z in V and all c in F, the following hold:
(a) 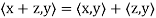
(b) 
(c) 
(d) 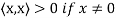
Note that (c) reduces to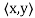 =
= 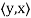 if F = R. Conditions (a) and (b) simply require that the inner product be linear in the first component.
if F = R. Conditions (a) and (b) simply require that the inner product be linear in the first component.
It is easily shown that if  and
and  , then
, then

Q11) What is an inner product space?
A11)
A vector space V over F endowed with a specific inner product is called an inner product space. If F = C, we call V a complex inner product It is clear that if V has an inner product  and W is a subspace of
and W is a subspace of
V, then W is also an inner product space when the same function 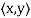 is
is
Restricted to the vectors x, y ∈ W.space, whereas if F = R, we call V a real inner product space.
Q12) What is Gram- Schmidt orthogonalization process?
A12)
Suppose { } is a basis of an inner product space V. One can use this basis to construct an orthogonal basis {
} is a basis of an inner product space V. One can use this basis to construct an orthogonal basis {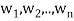 } of V as follows. Set
} of V as follows. Set



………………
……………….

In other words, for k = 2, 3, . . . , n, we define

Where
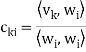
Is the component of 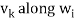 .
.
Each 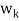 is orthogonal to the preceeding w’s. Thus,
is orthogonal to the preceeding w’s. Thus, form an orthogonal basis for V as claimed. Normalizing each wi will then yield an orthonormal basis for V.
form an orthogonal basis for V as claimed. Normalizing each wi will then yield an orthonormal basis for V.
The above process is known as the Gram–Schmidt orthogonalization process.
Q13) Apply the Gram–Schmidt orthogonalization process to find an orthogonal basis and then an orthonormal basis for the subspace U of  spanned by
spanned by

A13)
Step-1: First 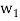 =
= 
Step-2: Compute

Now set- 
Step-3: Compute

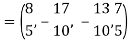
Clear fractions to obtain, 
Thus,  ,
,  ,
,  form an orthogonal basis for U. Normalize these vectors to obtain an orthonormal basis
form an orthogonal basis for U. Normalize these vectors to obtain an orthonormal basis
 of U. We have
of U. We have

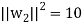
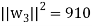
So

Q14) Find the orthogonal canonical form of the quadratic form.
5
A14)
The matrix form of this quadratic equation can be written as,
A = 
We can find the eigen values of A as –
|A -  | = 0
| = 0
 = 0
= 0

Which gives,
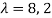
The required orthogonal canonical reduction will be,
8 .
.
Q15) What is the diagonalization of linear operators?
A15)
Consider a linear operator T: V  V. Then T is said to be diagonalizable if it can be represented by a diagonal matrix D. Thus, T is diagonalizable if and only if there exists a basis S = {
V. Then T is said to be diagonalizable if it can be represented by a diagonal matrix D. Thus, T is diagonalizable if and only if there exists a basis S = { } of V for which
} of V for which


………………
……………….

In such a case, T is represented by the diagonal matrix
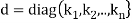
Relative to the basis S.
Unit – 8
Unit – 8
Unit – 8
Unit – 8
Unit – 8
Unit – 8
Inner product and Orthogonality
Q1) What is the norm of a vector?
A1)
By the third axiom of an inner product, <u, v> is nonnegative for any vector u. Thus, its positive square root exists. We use the notation

This nonnegative number is called the norm or length of u. The relation ||u||2 = <u, u> will be used frequently.
If ||u|| = 1 or, equivalently, if <u, u> = 1, then u is called a unit vector and it is said to be normalized. Every nonzero vector v in V can be multiplied by the reciprocal of its length to obtain the unit vector

Which is a positive multiple of v. This process is called normalizing v.
Q2) What is orthogonality?
A2)
Let V be an inner product space. The vectors u, v  V are said to be orthogonal and u is said to be orthogonal to v if
V are said to be orthogonal and u is said to be orthogonal to v if
<u, v> = 0
The relation is clearly symmetric—if u is orthogonal to v, then <v, u> = 0, and so v is orthogonal to u. We note that 0  V is orthogonal to every v
V is orthogonal to every v  V, because
V, because
Conversely, if u is orthogonal to every v 2 V, then <u, u> = 0 and hence u = 0 by third axiom: Observe that u and v are orthogonal if and only if cos y = 0, where y is the angle between u and v. Also, this is true if and only if u and v are ‘‘perpendicular’’—that is, y =  2 (or y = 90degree).
2 (or y = 90degree).
Q3) What is symmetric matrix?
A3)
In linear algebra, a symmetric matrix is a square matrix that is equal to its transpose. Formally, because equal matrices have equal dimensions, only square matrices can be symmetric. The entries of a symmetric matrix are symmetric with respect to the main diagonal. So, if aᵢⱼ denotes the entry in the i-th row and j-th column then for all indices i and j. Every square diagonal matrix is symmetric, since all off-diagonal elements are zero.
Any square matrix is said to be symmetric matrix if its transpose equals to the matrix itself.
For example:
 &
& 
Q4) Check whether the following matrix A is symmetric or not?
A = 
A4)
As we know that if the transpose of the given matrix is same as the matrix itself then the matrix is called symmetric matrix.
So that, first we will find its transpose,
Transpose of matrix A ,

Here,
A = 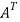
So that, the matrix A is symmetric.
Q5) Show that any square matrix can be expressed as the sum of symmetric matrix and anti- symmetric matrix.
A5)
Suppose A is any square matrix
Then,
A = 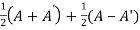
Now,
(A + A’)’ = A’ + A
A+A’ is a symmetric matrix.
Also,
(A - A’)’ = A’ – A
Here A’ – A is an anti – symmetric matrix
So that,
Square matrix = symmetric matrix + anti-symmetric matrix
Q6) Let A be a real symmetric matrix whose diagonal entries are all positive real numbers. Prove.
A6)
Is this true for all of the diagonal entries of the inverse matrix A-1 are also positive? If so, prove it. Otherwise give a counter example
Solution: The statement is false, hence we give a counter example
Let us consider the following 2 2 matrix
2 matrix
A = 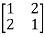
The matrix A satisfies the required conditions, that is A is symmetric and its diagonal entries are positive.
The determinant det(A) = (1)(1)-(2)(2) = -3 and the inverse of A is given by
A-1=  =
= 
By the formula for the inverse matrix for 2 2 matrices.
2 matrices.
This shows that the diagonal entries of the inverse matric A-1 are negative.
Q7) Let A and B be n n skew-matrices. Namely AT = -A and BT = -B
n skew-matrices. Namely AT = -A and BT = -B
(a) Prove that A+B is skew-symmetric.
(b) Prove that cA is skew-symmetric for any scalar c.
(c) Let P be an m n matrix. Prove that PTAP is skew-symmetric.
n matrix. Prove that PTAP is skew-symmetric.
A7)
(a) (A+B)T = AT + BT = (-A) +(-B) = -(A+B)
Hence A+B is skew symmetric.
(b) (cA)T = c.AT =c(-A) = -cA
Thus, cA is skew-symmetric.
(c)Let P be an m n matrix. Prove that PT AP is skew-symmetric.
n matrix. Prove that PT AP is skew-symmetric.
Using the properties, we get,
(PT AP)T = PTAT(PT)T = PTATp
= PT (-A) P = - (PT AP)
Thus (PT AP) is skew-symmetric.
Q8) What is quadratic form?
A8)
Quadratic form can be expressed as a product of matrices.
Q(x) = X’ AX,
Where,
X =  and A =
and A = 
X’ is the transpose of X,
X’AX = [ x1 x2 x3] 
= [ a11x1 + a21x2 + a31x3 a12x1 + a22x2 + a32x3 a13x1 + a23x2 + a33x3]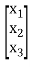
= a11x12 + a21x1x2 + a31 x1x3 + a12x1x2 + a22x22 +a32x2x3 + a13x1x3 + a23x2x3 + a33x32
= a11x12 + a22x22+a33x32+(a12+a21)x1x2 + (a23+ a32)x2x+(a31+ a13)x1x3
Which is the quadratic form.
Q9) Find the real matrix of the following quadratic form:
Q(x1, x2, x3) = x2 + 4x22 + 6x32 + 2x1x2 + x2x3 + 3x1x3
A9)
Here we will compare the coefficients with the standard quadratic equation,
We get,
a11 = 1, a22 = 4, a33 = 6, a12 = 2, a21 = 0, a23 = 1, a32 = 0, a13 = 3, a31 = 0
Q(x1, x2, x3) = [x1 x2 x3] = [ x1 2x1+4x2 3x1 + x2+ 6x3]
= [ x1 2x1+4x2 3x1 + x2+ 6x3] 
= x12 + 2x1x2 + 4x22 + 3x1x3 + x2x3 + 6x32
Q10) What is inner product?
A10)
Let V be a vector space over F. An inner product on V is a function that assigns, to every ordered pair of vectors x and y in V, a scalar in F, denoted 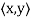 , such that for all x, y, and z in V and all c in F, the following hold:
, such that for all x, y, and z in V and all c in F, the following hold:
(a) 
(b) 
(c) 
(d) 
Note that (c) reduces to =
=  if F = R. Conditions (a) and (b) simply require that the inner product be linear in the first component.
if F = R. Conditions (a) and (b) simply require that the inner product be linear in the first component.
It is easily shown that if  and
and  , then
, then

Q11) What is an inner product space?
A11)
A vector space V over F endowed with a specific inner product is called an inner product space. If F = C, we call V a complex inner product It is clear that if V has an inner product  and W is a subspace of
and W is a subspace of
V, then W is also an inner product space when the same function  is
is
Restricted to the vectors x, y ∈ W.space, whereas if F = R, we call V a real inner product space.
Q12) What is Gram- Schmidt orthogonalization process?
A12)
Suppose { } is a basis of an inner product space V. One can use this basis to construct an orthogonal basis {
} is a basis of an inner product space V. One can use this basis to construct an orthogonal basis { } of V as follows. Set
} of V as follows. Set
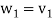
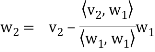

………………
……………….

In other words, for k = 2, 3, . . . , n, we define

Where

Is the component of  .
.
Each  is orthogonal to the preceeding w’s. Thus,
is orthogonal to the preceeding w’s. Thus, form an orthogonal basis for V as claimed. Normalizing each wi will then yield an orthonormal basis for V.
form an orthogonal basis for V as claimed. Normalizing each wi will then yield an orthonormal basis for V.
The above process is known as the Gram–Schmidt orthogonalization process.
Q13) Apply the Gram–Schmidt orthogonalization process to find an orthogonal basis and then an orthonormal basis for the subspace U of  spanned by
spanned by

A13)
Step-1: First  =
= 
Step-2: Compute

Now set- 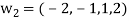
Step-3: Compute


Clear fractions to obtain, 
Thus,  ,
,  ,
,  form an orthogonal basis for U. Normalize these vectors to obtain an orthonormal basis
form an orthogonal basis for U. Normalize these vectors to obtain an orthonormal basis
 of U. We have
of U. We have
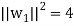


So

Q14) Find the orthogonal canonical form of the quadratic form.
5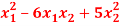
A14)
The matrix form of this quadratic equation can be written as,
A = 
We can find the eigen values of A as –
|A -  | = 0
| = 0
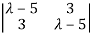 = 0
= 0
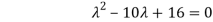
Which gives,

The required orthogonal canonical reduction will be,
8 .
.
Q15) What is the diagonalization of linear operators?
A15)
Consider a linear operator T: V  V. Then T is said to be diagonalizable if it can be represented by a diagonal matrix D. Thus, T is diagonalizable if and only if there exists a basis S = {
V. Then T is said to be diagonalizable if it can be represented by a diagonal matrix D. Thus, T is diagonalizable if and only if there exists a basis S = { } of V for which
} of V for which


………………
……………….

In such a case, T is represented by the diagonal matrix

Relative to the basis S.