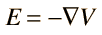Unit 5

Q 1 Define electric charge?

Answer:

Positively Charged Particles

In this type of particles, numbers of positive ions are larger than the numbers of negative ions. Means, the numbers of protons are larger than the number of electrons. To neutralize positively charged particles, electrons from the surroundings come to this particle until the number of protons and electrons become equal.

Negatively Charged Particles

Similarly, numbers of electrons are larger than the number of protons. To neutralize negatively charged particles, since protons cannot move and cannot come to negatively charged particles, electrons moves to the ground or any other particle around

Neutral Particles

Include equal numbers of protons and electrons. They have both protons, neutrons and electrons however, numbers of positive ions are equal to the numbers of negative ions.

Q 2 Explain Div and Curl for electrostatics?

Answer:

This approach can be considered to arise from one of Maxwell's equations and involves the vector calculus operation called the divergence. The divergence of the electric field at a point in space is equal to the charge density divided by the permittivity of space.

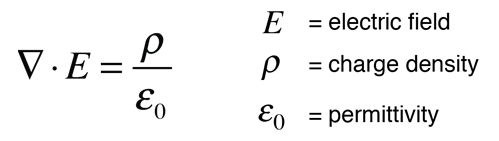
In a charge-free region of space where r = 0, we can say

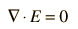
While these relationships could be used to calculate the electric field produced by a given charge distribution, the fact that E is a vector quantity increases the complexity of that calculation. It is often more practical to convert this relationship into one which relates the scalar electric potential to the charge density

The curl of a vector field E = E (x, y, z) is defined, in terms of the del operators ∇, like a cross product

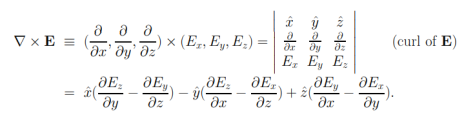
The proof of curl-free nature of static electric fields can be given by first showing that Coulomb field of a static charge is curl-free, and then making use of the superposition principle along with the fact that the curl of a sum must be the sum of curls — like differentiation, “taking curl” is a linear operation

Q 3 Two balloons are charged with an identical quantity and type of charge:

-6.25 nC. They are held apart at a separation distance of 61.7 cm. Determine the magnitude of the electrical force of repulsion between them.

Answer:

The final step of the strategy involves substituting known values into the Coulomb's law equation and using proper algebraic steps to solve for the unknown information. This substitution and algebra is shown below.

Felect = k • Q1 • Q2 / d2

Felect = (9.0 x 109 N•m2/C2) • (6.25 x 10-9 C) • (6.25 x 10-9 C) / (0.617 m)2

Felect = 9.23 x 10-7 N

Q 4. Explain poler and non poler dielectrics?

Answer:

A polar molecule is one in which the ‘centres of gravity’ of the positive charges (i.e., protons) and negative charges (i.e., electrons) do not coincide. Such molecules are called permanent electric dipoles as these have permanent dipole moments. Some common polar molecules are HCl, H2O, N2O, NH3, H2S, C2H5OH, SO2.

In a molecule of HCl, there is an excess positive charge on the H-ion and an equal negative charge on the Cl-ion. The molecule, therefore, has a dipole moment at every instant and is a polar molecule. Another interesting example of polar molecules is H2O

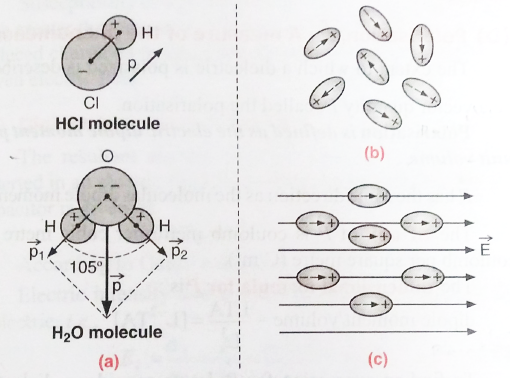
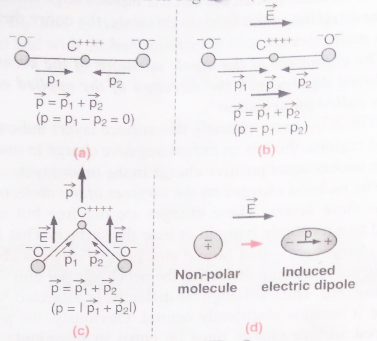
A non-polar molecule is one in which the centres of gravity of positive charges (i.e., protons) and negative charges (i.e., electrons) coincide. These molecules, thus, do not have any permanent dipole moment.

Some common examples of non-polar molecules are CO2, CCl4, oxygen (O2), nitrogen (N2), hydrogen (H2), methane (CH4) and ethane (C2H6).

In a molecule of CO2, the oxygen ions are symmetrically placed with respect to the carbon ion, hence the dipole moment is zero

Q 5. What are the maxwell equation in vacuum?

Answer:

Maxwell's equations represent one of the most elegant and concise ways to state the fundamentals of electricity and magnetism. From them one can develop most of the working relationships in the field. Because of their concise statement, they embody a high level of mathematical sophistication and are therefore not generally introduced in an introductory treatment of the subject, except perhaps as summary relationships.

These basic equations of electricity and magnetism can be used as a starting point for advanced courses, but are usually first encountered as unifying equations after the study of electrical and magnetic phenomena.

Integral form in the absence of magnetic or polarizable media:

I. Gauss' law for electricity

II. Gauss' law for magnetism

III. Faraday's law of induction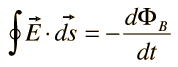

IV. Ampere's law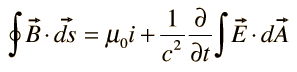

Q 6. What is pointing vector?

Answer:

 The energy density moves with the electric and magnetic fields in a similar manner. The energy per unit area per unit time passing through a plane perpendicular to the wave, called the energy flux and denoted by S, can be calculated by dividing the energy by the area A and the time interval Δt.

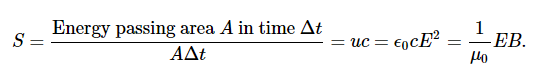
More generally, the flux of energy through any surface also depends on the orientation of the surface. To take the direction into account, we introduce a vector S→, called the Poynting vector, with the following definition:

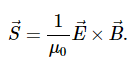
Q 7. Define Current Displacement?

Answer:

Electric displacement, denoted by D, is the charge per unit area that would be displaced across a layer of conductor placed across an electric field. It is also known as electric flux density.

Electric displacement is used in the dielectric material to find the response of the materials on the application of an electric field E. In Maxwell’s equation, it appears as a vector field.

The SI unit of electric displacement is Coulomb per meter square (C m-2).

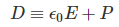
Where,

• ϵ0: Vacuum permittivity
• P: Polarization density
• E: Electric field
• D: Electric displacement field

It was found that if electric field E is applied on the dielectric material, the bound charges inside the material responds to the electric field such that the distribution of positive changes take place in the direction of the electric field while the distribution of negative charges takes place in the opposite direction of the electric field. Before the application of the electric field, the material is electrically neutral and there is a formation of electric dipoles

Q 8 What are the continuity equation for current densities?

Answer:

The Continuity Equation

If we do some simple mathematical tricks to Maxwell's Equations, we can derive some new equations. On this page, we'll look at the continuity equation, which can be derived from Gauss' Law and Ampere's Law.

To start, I'll write out a vector identity that is always true, which states that the divergence of the curl of any vector field is always zero:

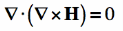If we apply the divergence to both sides of Ampere's Law, then we obtain:

If we apply Gauss' Law to rewrite the divergence of the Electric Flux Density (D), we have derived the continuity equation:

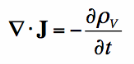Q 9 Define Stokes theorem?

Answer:

Stokes Theorem (also known as Generalized Stoke’s Theorem) is a declaration about the integration of differential forms on manifolds, which both generalizes and simplifies several theorems from vector calculus. As per this theorem, a line integral is related to a surface integral of vector fields. 

The Stoke’s theorem states that “the surface integral of the curl of a function over a surface bounded by a closed surface is equal to the line integral of the particular vector function around that surface.”

∮CF⃗.dr→=∬S (▽×F⃗ ).dS→

Where,

C = A closed curve.

S = Any surface bounded by C.

F = A vector field whose components have continuous derivatives in an open region of R3 containing S.

This classical declaration, along with the classical divergence theorem, fundamental theorem of calculus, and Green’s theorem are exceptional cases of the general formulation specified above.

If you walk in the positive direction around C with your head pointing in the direction of n, the surface will always be on your left.

S is an oriented smooth surface bounded by a simple, closed smooth-boundary curve C with positive orientation.

Q 10. Give the formulation of Gauss Theorem?

Answer:

According to Gauss’s theorem the net-outward normal electric flux through any closed surface of any shape is equivalent to 1/ε0 times the total amount of charge contained within that surface

Proof of Gauss’s Theorem Statement:

• Let the charge be = q
• Let us construct the Gaussian sphere of radius = r

Now, Consider, A surface or area ds having ds (vector)

Normal having the flux at ds:

Flux at ds:

d e = E (vector) d s (vector) cos θ

But, θ = 0

Therefore, Total flux:

C = f d Φ

E 4 π r2

Therefore,

σ = 1 / 4πɛo q / r2 × 4π r2

σ = q / ɛo

Q 11. What is Potential Gradient?

Answer:  One of the values of calculating the scalar electric potential (voltage) is that the electric field can be calculated from it. The component of electric field in any direction is the negative of rate of change of the potential in that direction.

If the differential voltage change is calculated along a direction ds, then it is seen to be equal to the electric field component in that direction times the distance ds.

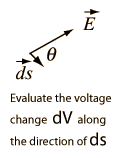
The electric field can then be expressed as

For rectangular coordinates, the components of the electric field are

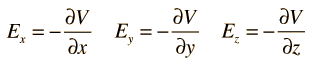Express as a gradient.

The expression of electric field in terms of voltage can be expressed in the vector form

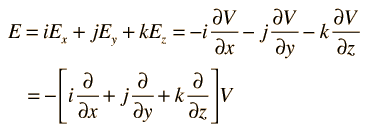
This collection of partial derivatives is called the gradient, and is represented by the symbol ∇. The electric field can then be written