MODULE 4

Question-1: The set of all

Sol. V is an abelian group with respect to addition of matrices in groups.

The null matrix of m by n is the additive identity of this group.

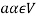If then as 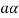is also the matrix of m by n with elements of real numbers.

So that V is closed with respect to scalar multiplication.

We conclude that from matrices-

1.

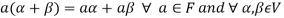
2.

3.

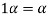
4.  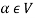  Where 1 is the unity element of F.

Therefore we can say that V (F) is a vector space.

Question-2: The vector space of all real valued continuous (differentiable or integrable) functions defined in some interval [0,1]

Suppose f and g are two functions, and V denotes the set of all real valued continuous functions of x defined in the interval [0,1]

Then V is a vector space over the filed R with vector addition and multiplication as:

And

Here we will first prove that V is an abelian group with respect to addition composition as in rings.

V is closed with respect to scalar multiplication since af is also a real valued continuous function

We observe that-

1. If 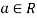and f,g 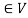, then

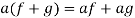
2. If 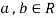  and 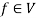 , then

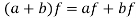
3. If   and  , then

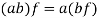
4. If 1 is the unity element of R and 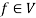, then

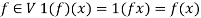
So that V is a vector space over R.

Question-3: If 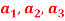are fixed elements of a field F, then set of W of all ordered triads ( 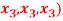of elements of F,

Such that-

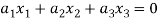
Is a subspace of

Sol. Suppose 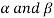are any two elements of W.

Such that

And these are the elements of F, such that-

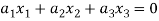          …………………….. (1)

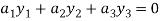         …………………….  (2)

If a and b are two elements of F, we have

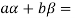
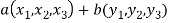
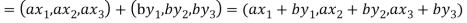
Now

              = 

              =

              =

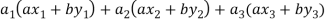
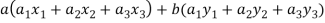
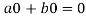
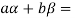
So that W is subspace of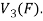

Question-4: Let R be a field of real numbers. Now check whether which one of the following are subspaces of

1. {

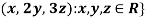
2. {

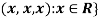
3. {

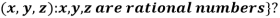
Solution- 1. Suppose W = {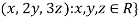

Let 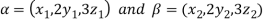be any two elements of W.

If a and b are two real numbers, then-

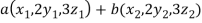
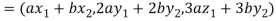
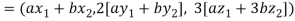
Since 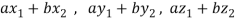are real numbers.

So that and   or  

So that W is a subspace of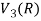

2. Let W = {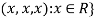

Let 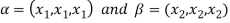be any two elements of W.

If a and b are two real numbers, then-

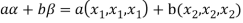
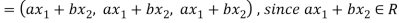
So that W is a subspace of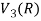

3. Let W ={

Now 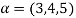is an element of W. Also 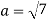is an element of R.

But 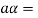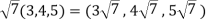which do not belong to W.

Since 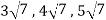are not rational numbers.

So that W is not closed under scalar multiplication.

W is not a subspace of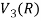

Question-5: If the set S = of vector V(F) is linearly independent, then none of the vectors can be zero vector.

Sol.  Let 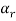be equal to zero vector where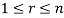

Then

For any 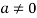in F.

Here 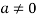therefore from this relation we can say that S is linearly dependent. This is the contradiction because it is given that S is linearly independent.

Hence none of the vectors can be zero.

We can conclude that a set of vectors which contains the zero vector is necessarily linear dependent.

Question-6: Show that S = {(1 , 2 , 4) , (1 , 0 , 0) ,  (0 , 1 , 0) , (0 , 0 , 1)} is linearly dependent subset of the vector space 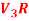. Where R is the field of real numbers.

Sol.  Here we have-

1 (1 , 2 , 4) + (-1) (1 , 0 , 0) + (-2) (0 ,1, 0) + (-4) (0, 0, 1)

= (1, 2 , 4) + (-1 , 0 , 0) + (0 ,-2, 0) + (0, 0, -4)

= (0, 0, 0)

That means it is a zero vector.

In this relation the scalar coefficients 1 , -1 ,  -2, -4 are all not zero.

So that we can conclude that S is linearly dependent.

Question-7: If are linearly independent vectors of V(F).where F is the field of complex numbers, then so also are .

Sol. Suppose a, b, c are scalars such that-

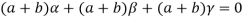                                            …………….. (1)

But are linearly independent vectors of V(F), so that equations (1) implies that-

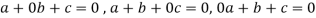
The coefficient matrix A of these equations will be-

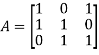
Here we get rank of A = 3, so that a = 0, b = 0, c = 0 is the only solution of the given equations, so that 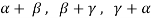are also linearly independent.

Question-8: Show that the vectors (1, 2, 1), (2, 1, 0) and (1, -1, 2) form a basis of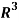

Sol. We know that set {(1,0,0) , (0,1,0) , (0,0,1)} forms a basis of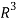

So that dim .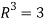

Now if we show that the set S = {(1, 2, 1), (2, 1, 0) , (1, -1, 2)} is linearly independent, then this set will form a basis of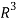

We have,

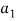                  (1, 2, 1)+ 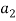(2, 1, 0)+ 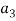(1, -1, 2) = (0, 0, 0)

                   (

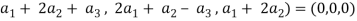
Which gives-

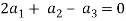
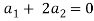
On solving these equations we get,

So we can say that the set S is linearly independent.

Therefore it forms a basis of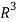

Question-9: Test whether the vectors (1,-1,1),(2,1,1) and (3,0,2) are linearly dependent.If so write the relationship for the vectors.

Solution:

Let the given vectors be,

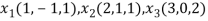
Now we have to write the given vectors in the form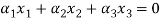

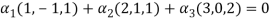
1

-1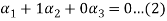

  1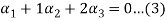

From the second equation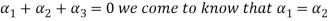

Now we substitute this value in equation (1)

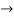
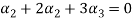
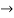
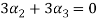
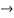
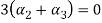
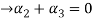
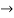
Now substituting and 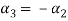in the third equation

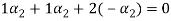
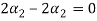
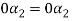....(4)

Equation (4) is true for any value of 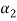. So that let us assume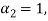 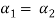and

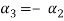
Values of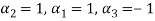 

Therefore we can say that given vectors are linearly dependent.

Now the relationship is given by

Applying the values in the equation we will get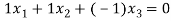

Question-10: Let U= {(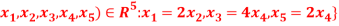 be a subspace of R5.Findd basis of U.

Solution :

U=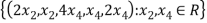

Therefore we have that is a basis of U.To verify this,

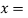( then we have that:

( =

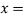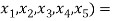
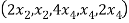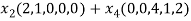
So U = span((2,1,0,0,0),(0,0,4,1,2)) .Now consider the following vector equation for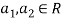

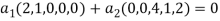
The equation above implies that

Thus 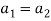and so 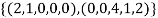is a linearly independent set of vectors in U.

Thus 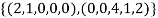is a basis of U.