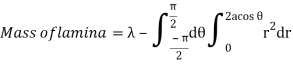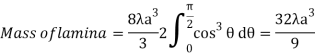UNIT 2

Question-1: Evaluate

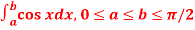
Sol. Here we notice that  f:x→cos x  is a decreasing function on [a , b],

Therefore by the definition of the definite integrals-

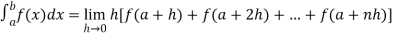
Then

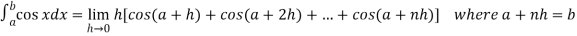
Now,

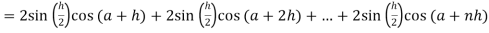
Here

Thus

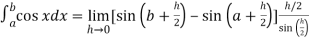
Question-2: Evaluate   0∞ x3/2 e -x dx

Solution:               0∞ x3/2 e -x dx          =   0∞ x 5/2-1  e -x dx  

= γ (5/2)

         =   γ (3/2+ 1) 

         =    3/2   γ (3/2 )  

        =   3/2.  ½   γ (½ )

= 3/2 .½.π 

        =    ¾ π  

Question-3: Determine the area enclosed by the curves-

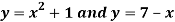
Sol. We know that the curves are equal at the points of interaction, thus equating the values of y of each curve-

Which gives-

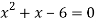
By factorization,

Which means,

                                      x = 2 and x = -3

By determining the intersection points the range the values of x has been found-

x	-3	-2	-1	0	1	2
1	10	5	2	1	2	5

And

We get the following figure by using above two tables-

Area of shaded region =

                                          =

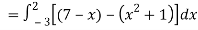
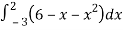
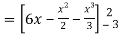
                                         = ( 12 – 2 –  8/3 ) – (-18 – 9/2 + 9)

                                        =

                                        = 125/6 square unit

Question-4: Evaluate    I   =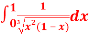  

Solution:

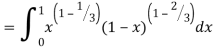
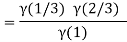
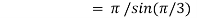
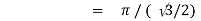
                          = 2 π/3

Question-5: Find the area enclosed by the two functions-

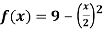                      and g(x) = 6 – x

Sol. We get the following figure by using these two equations                                 

To find the intersection points of two functions f(x) and g(x)-

                                             f(x) = g(x)

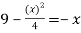
On factorizing, we get-

                                                  x = 6, -2

Now

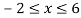
Then, area under the curve-

                                        A =

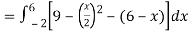
Therefore the area under the curve is 64/3 square unit.

Question-6: Find the volume of the solid of revolution formed by revolving R around y-axis of the function f(x) = 1/x over the interval [1 , 3].

Sol. The graph of the function f(x) = 1/x will look like-

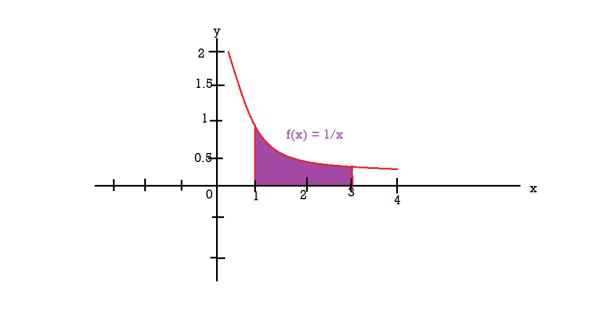
The volume of the solid of revolution generated by revolving R(violet region) about the y-axis over the interval [1 , 3]

  Then the volume of the solid will be-

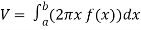
Question-7: Find the volume of the solid of revolution formed by revolving R around y-axis of the function f(x) = 2x - x² over the interval [0 , 2].

Sol. The graph of the function f(x) = 2x - x² will be-

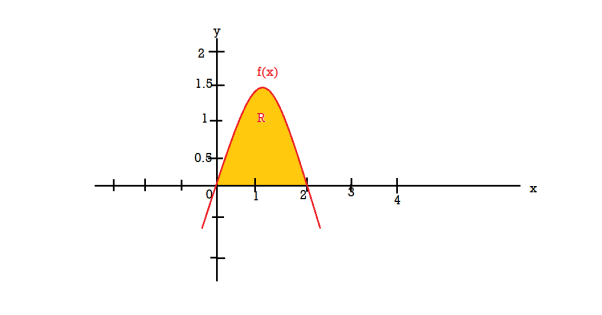
The volume of the solid is given by-

                                                  =

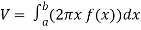
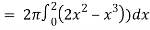
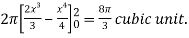
Question-8: Evaluate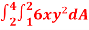 , where dA is the small area in xy-plane.

Sol.    

Let,     I =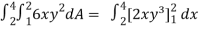 

                                                       =

                                                      = 

                                                       = 

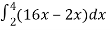
                                                       =    84 sq. Unit.

Which is the required area.

Question-9: Evaluate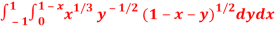

Sol. Let us suppose the integral is I,

                            I =

Put c = 1 – x in I, we get

                           I =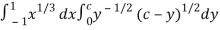

    Suppose , y = ct

      then dy = c

Now we get,

                       I =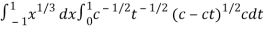

                      I =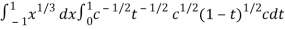

                    I =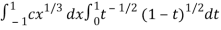

                     I =

                    I  =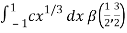

           As we know that by beta function,

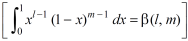
         Which gives,

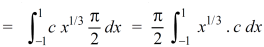
Now put the value of c, we get

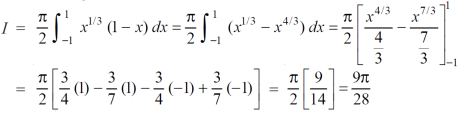
Question-10: Evaluate 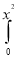ey/x dy dx.

Sol.

Given: I = 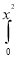ey/x dy dx

Here limits of inner integral are functions of y therefore integrate w.r.t y,

I = dx

                                     =            

                                    =

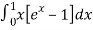
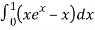
I =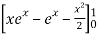

                                    =            =

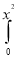ey/x dy dx=

Question-11: Evaluate

Sol.

Let,I =

Here limits for both x and y are constants, the integral can be evaluated first w.r.t any of the variables x or y.

I = dy 

I=

                                     =          

=          

                                     =          

                                     = 

                                    =

=

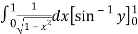
Question-12: Evaluate 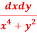         over x  1, y 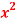

Sol.

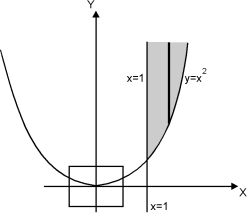Let      I=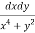           over x  1, y 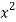

The region bounded by x  1 and y 

Is as shown in Fig. 6.3.

Fig. 6.3

Take a vertical strip along strip x constant and y varies from y =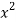

To y = . Now slide strip throughout region keeping parallel to y-axis. Therefore y constant and x varies from x = 1 to x = .

I=               

                         =             

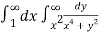
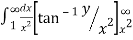=                  [ ∵ dx = tan–1 (x/a)]

= =

=– = (0 – 1)

    I =

Question-13: Evaluate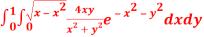

Soln. :

The region of integration bounded by

y = 0, y = 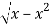and x = 0, x = 1

y =  x2 + y2 = x

The region bounded by these is as shown in Fig

Convert the integration in polar co-ordinates by using x = r cos , y = r sin  and dx dy = r dr d

 x2 + y2= x becomes r = cos 

y = 0 becomes r sin  = 0  = 0

x = 0 becomes r cos  = 0  =

And x = 1 becomes r = sec                       Fig. 6.8

Take a radial strip SR with angular thickness , Along strip  constant and r varies from r = 0 to r = cos . Turning strip throughout region therefore  varies from = 0 to  =

   I = r dr d

= 4 cos  sin 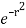 d r dr

= 4 cos  sin  d [–]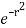

= – 2 cos  sin  [+1] d

= – 2 [cos  sin 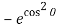 – cos  sin ] d

=   –2 + 2 cos  sin  d

=   – + 2

= + 1 =

Question-14: Evaluate  r sin  dr d over the cardioid r = a (1 – cos ) above the initial line.

Soln. :

The cardioid r = a (1 – cos ) is as shown in Fig. 6.11. The region of the integration is above the initial line.

Take a radial strip SR, along strip  constant and r Varies from r = 0 to r = a (1 – cos ).

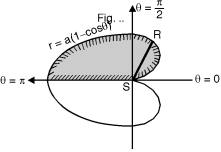New turning the strip throughout region therefore  varies from  = 0 to  = .

   I= r sin  dr d

= sin  d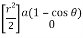

Fig.6.11

=sin  [a2 (1 – cos )2]

                                      =   

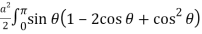
I= (sin   – 2 sin  cos  + sin ) d

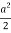=     2 (sin   – sin2  + sin 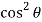) d

=+

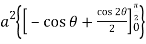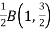
I= a2= a2

I=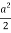

Question-15: Find the area enclosed by two curves using double integration.

                                           y = 2 – x and y² = 2 (2 – x)

Sol.  Let,

                         y =  2 – x  ………………..(1)

And                y² = 2 (2 – x) ………………..(2)

On solving eq. (1) and (2)

We get the intersection points  (2,0) and (0,2) ,

We know that,

                                             Area =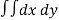

Here we will find the area as below,

                                           Area =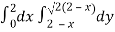

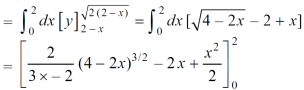
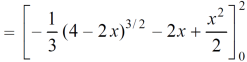
Which gives,

                                                   = ( - 4 + 4 /2 ) + 8 / 3  = 2 / 3.

Question-16: Find the are lying inside a cardioid r = 1 + cos θ and ouside the parabola r(1 + cos θ) = 1.

Sol. Let,

                          r = 1 + cos θ   ……………………..(1)

                         r(1 + cos θ) = 1……………………..(2)

Solving these equestions , we get

(1 + cos θ )( 1 + cos θ ) = 1

                  (1 + cos θ )² = 1

                          1 + cos θ    = 1

Cos θ = 0  

θ = ±π / 2  

So that, limits of r are,

                         1 + cos θ    and 1 / 1 + cos θ  

The area can be founded as below,

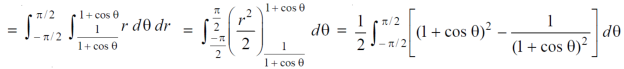
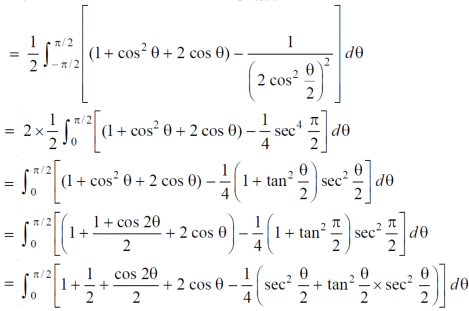
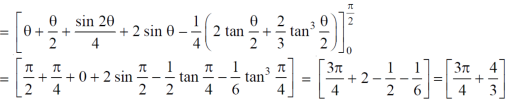
Question-17: Evaluate   

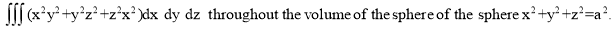
Solution:-                  

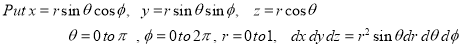
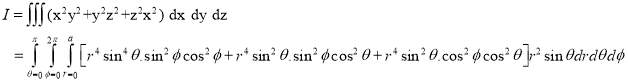
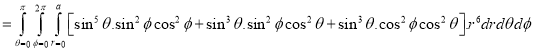
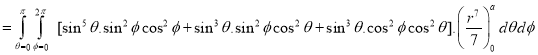
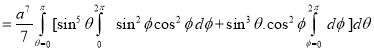
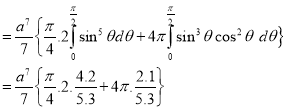
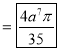
Question-18: If the density at  any point of a non-uniform circular lamina of radius’ a’ varies as its distance from a fixed point on the circumference of the circle then  find  the mass of lamina.

Solution:

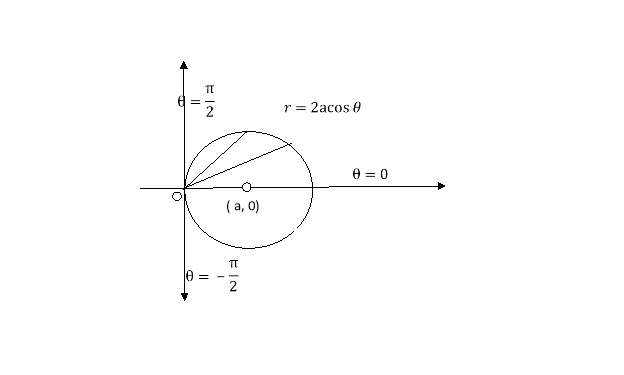
Take the fixed point on the circumference of the circle as origin and diameter through it as x axis. The polar equation of circle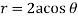

And density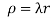.