Module 5

Matrices

Question and answer

1. Reduce the following matrix to normal form of Hence find it’s rank,

Solution:

We have,

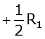
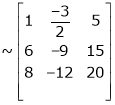
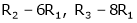
Apply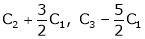

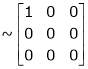
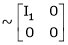
Rank of A = 1

2.     Find the rank of the matrix

Solution:

We have,

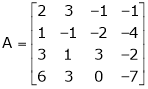
Apply R12

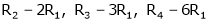
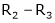
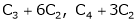
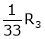
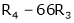
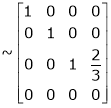
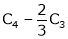
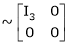
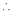Rank of A = 3

3.     Find the rank of the following matrices by reducing it to the normal form.

Solution:

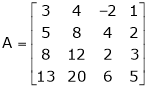
Apply C14

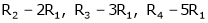
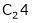
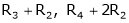
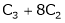
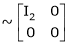
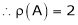
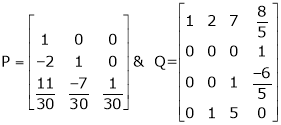
4.     If 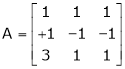Find Two

Matrices P and Q such that PAQ is in normal form.

Solution:

Here A is a square matrix of order 3 x 3. Hence we write,

A = I3 A.I3

i.e.

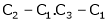
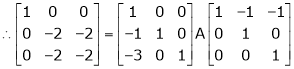
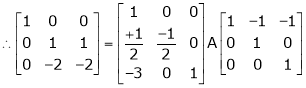
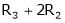
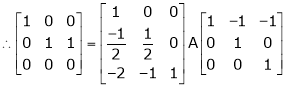
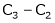
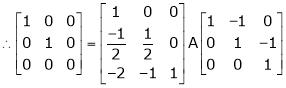
i.e.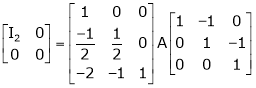

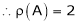
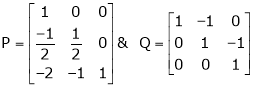
5.     Find a non – singular matrices p and Q such that P A Q is in normal form where

Solution:

Here A is a matrix of order 3 x 4. Hence we write A as,

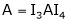
i.e.

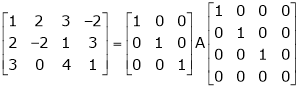
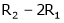
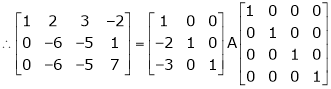
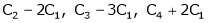
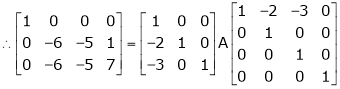
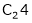
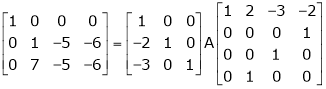
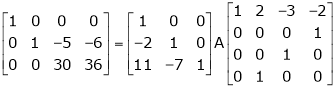
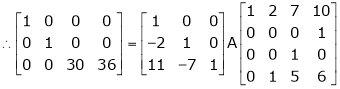
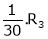
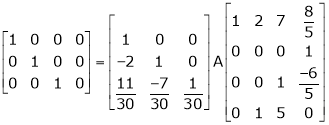
i.e.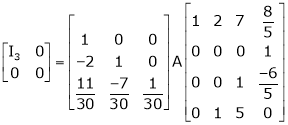

6.     Solve the equations:

Let the coefficient matrix be A =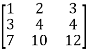  

Apply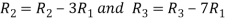

A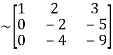

Apply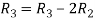 

         A

Since |A| ,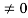 

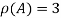
Also number of equation is m=3 and number of unknowns n=3

Since rank of coefficient matrix A = n number of unknowns

The system of equation   is consistent and has trivial zero solution.

That is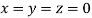  

7.     Solve completely the system of equations

Solution: We can write the given system of equation as AX=0

                     Or

Where coefficient   matrix A  =

    Apply 

A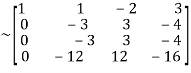  

Apply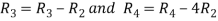

          A        …(i)

Since  |A|=0   and  also 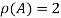, number of  equations m =4  and   number  of unknowns  n=4.

Here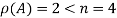 

So that the system has (n-r) linearly independent solution.

Let

Then from equation (i) we get

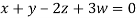
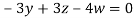
Putting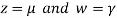 

We get 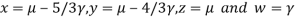  has infinite   number solution.

8.     Are the vectors 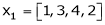, , 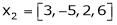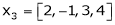linearly dependent. If so, express x1 as a linear combination of the others.

Solution:

Consider a vector equation,

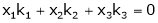
i.e.

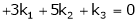
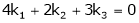
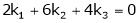
Which can be written in matrix form as,

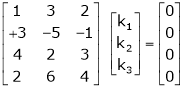
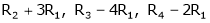
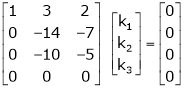
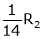
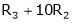
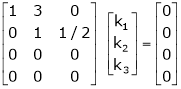
Here & no. Of unknown 3. Hence the system has infinite solutions. Now rewrite the questions as,

Put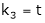

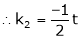and

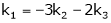
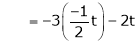
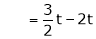
Thus

i.e.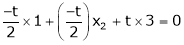

i.e.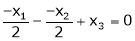

Since F11 k2, k3 not all zero. Hence are linearly dependent.

9.     Examine whether the following vectors are linearly independent or not.

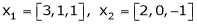and .

Solution:

Consider the vector equation,

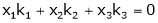
i.e. 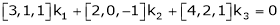… (1)

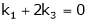
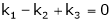
Which can be written in matrix form as,

R12

R2 – 3R1, R3 – R1

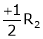
R3 + R2

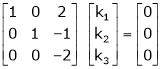
Here Rank of coefficient matrix is equal to the no. Of unknowns. i.e. r = n = 3.

Hence the system has unique trivial solution.

i.e.

i.e. vector equation (1) has only trivial solution. Hence the given vectors x1, x2, x3 are linearly independent

10. Determine the eigen values of eigen vector of the matrix.

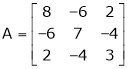
Solution:

Consider the characteristic equation as,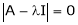

i.e.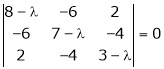

i.e.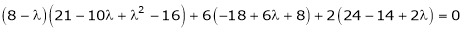

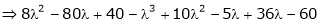
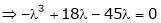
i.e.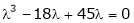

Which is the required characteristic equation.

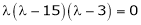
are the required eigen values.

Now consider the equation

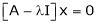… (1)

Case I:

If Equation (1)becomes

R1 + R2

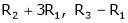
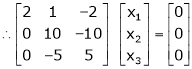
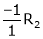
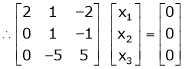
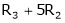
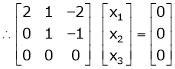
Thus

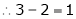independent variable.

Now rewrite equation as,

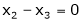
Put x3 = t

&

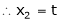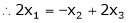
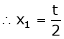
Thus .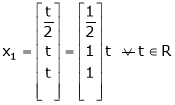

Is the eigen vector corresponding to .

Case II:

If equation (1) becomes,

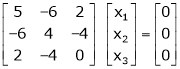
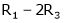
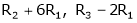
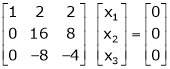
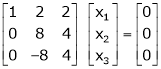
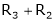
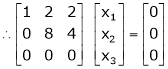
Here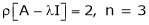

independent variables

Now rewrite the equations as,

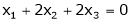
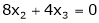
Put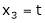

&

.

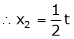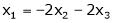
Is the eigen vector corresponding to .

Case III:

If equation (1) becomes,

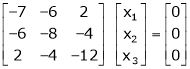
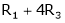
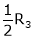
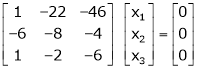
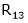
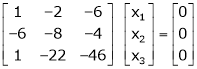
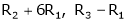
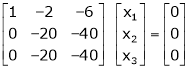
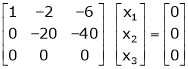
Here rank of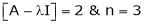

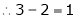independent variable.

Now rewrite the equations as,

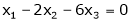
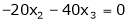
Put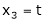

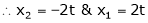
Thus .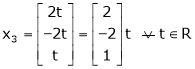

Is the eigen vector for .