Unit - 2
Linear algebra
Q1) Define vector space.
A1)
We define a vector space V where K is the field of scalars as follows-
Let V be a nonempty set with two operations-
(i) Vector Addition: This assigns to any u; v 
V a sum u + v in V.
(ii) Scalar Multiplication: This assigns to any u 
V, k 
K a product ku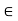 
V.
Then V is called a vector space (over the field K) if the following axioms hold for any vectors u; v; w 
V:
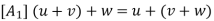
There is a vector in V, denoted by 0 and called the zero vector, such that, for any u 
V;
For each u 
V; there is a vector in V, denoted by -u, and called the negative of u, such that
u + (-u) (-u) + u = 0
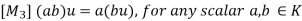
Q2) Define vector.
A2)
An ordered n – touple of numbers is called an n – vector. Thus the ‘n’ numbers x1, x2, …………xn taken in order denote the vector x. i.e. x = (x1, x2, ……., xn).
Where the numbers x1, x2, ………..,xn are called component or co – ordinates of a vector x. A vector may be written as row vector or a column vector.
Q3) What is linear independence?
A3)
A set of r vectors x1, x2, ………….,xr is said to be linearly independent if there exist scalars k1, k2, …………, kr all zero such that
x1 k1 + x2 k2 + …….. + xrkr = 0
Q4) Define linear combination.
A4)
A vector x can be written in the form.
x = x1 k1 + x2 k2 + ……….+xrkr
Where k1, k2, ………….., kr are scalars, then X is called linear combination of x1, x2, ……, xr.
Q5) What is linear span?
A5)
Suppose 
are any vectors in a vector space V. Recall that any vector of the form 
, where the ai are scalars, is called a linear combination of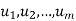 
.
The collection of all such linear combinations, denoted by Span(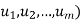
or span(
Clearly the zero vector 0 belongs to span
, because
0 = 0u1 + 0u2 + . . . + 0um
Furthermore, suppose v and v’ belong to span
,, say,
v = a1u1 + a2u2 + . . . + amum and v’ =b1u1 + b2u2 + . . . + bmum
Then
v + v’ = (a1 + b1)u1 + (a2 + b2)u2 + . . . + (am + bm)um
And, for any scalar k belongs to K,
Kv = ka1u1 + ka2u2 + . . . + kamum
Thus, v + v’ and kv also belong to span
. Accordingly, span
is a subspace of V.
Q6) Are the vectors x1 = [1, -3, 4, 2],x2 = [3, -5, 2,6], x3 =[2, -1, 3, 4] linearly dependent. If so, express x1 as a linear combination of the others.
A6)
Consider a vector equation,
x1k1 + x2k2 + x3k3 = 0
i.e., [1, -3, 4, 2]k1 + [3, -5, 2,6]k2 + [2, -1, 3, 4]k3 = [0, 0, 0, 0]
∴ k1 +3k2 + 2k3 = 0
+3k1 + 5k2 + k3 = 0
4k1 + 2k2 + 3k3 = 0
2k1 + 6k2 + 4k3 =0
Which can be written in matrix form as,
R2 + 3R1, R3 – 4R1, R4 – 2R1
1/14 R2
R3 + 10R2
Here ρ(A) = 2 & no. Of unknown 3. Hence the system has infinite solutions. Now rewrite the questions as,
k1 + 3k2 + 2k3 =0
k2 + ½ k3 =0
Put k3 =t
k2 = -1/2 t and
k1 = -3k2 – 2k3
= - 3 (- ½ t) -2t
= 3/2 t – 2t
= - t/2
Thus k1 = - t/2, k2 = -1/2 t – k3 = t ∀ t ∈ R
i.e., - t/2 × 1 + ( - t/2) x2 + t × 3 = 0
i.e.,- x1/2 – (-x2/2) + x3 = 0
- x1 – x2 + 2 x3 = 0
x1 = - x2 + 2 x3
Since F11k2, k3 not all zero. Hence x1, x2, x3 are linearly dependent.
Q7) At what value of P the following vectors are linearly independent.
[1, 3, 2], [2, P+7, 4], [1, 3, P+3]
A7)
Consider the vector equation.
[1, 3, 2]k1 + [2, P+7, 4]k2 + [1, 3, P+3]k3 = 0
i.e.
k1 + 2k2 + k3 = 0
3k1 + (p + 7)k2 + 3k3 = 0
2k1 + 4k2 + (P +3)k3 = 0
This is a homogeneous system of three equations in 3 unknowns and has a unique trivial solution.
If and only if Determinant of coefficient matrix is non zero.
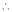consider 
.
i.e.,
1[(P + λ)(P+3) – 12] – 2[3(P+3) – 6] + 1[12 – (2P + 14)] 
0
P2 + 10P + 21 – 12 -6P – 6 – 2P – 2 
P2 + 2P + 1 
(P + 1)2 
(P + 1) 
P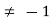 
Thus for 
the system has only trivial solution and Hence the vectors are linearly independent.
Q8) What is characteristic equation?
A8)
Let A he a square matrix, λ be any scalar then |A – λI| = 0 is called characteristic equation of a matrix A.
Note:
Let a be a square matrix and ‘λ’ be any scalar then,
1) [A – λI] is called characteristic matrix
2) | A – λI| is called characteristic polynomial.
The roots of a characteristic equations are known as characteristic root or latent roots, Eigen values or proper values of a matrix A.
Q9) What is Eigne vector?
A9)
Suppose λ1 be an Eigen value of a matrix A. Then ∃ a non – zero vector x1 such that.
[A – λI] x1 = 0 ...(1)
Such a vector ‘x1’ is called as Eigen vector corresponding to the Eigen value λ1
Q10) Find the sum and the product of the Eigen values of 
?
A10)
The sum of Eigen values = the sum of the diagonal elements
=1+(-1)=0
The product of the Eigen values is the determinant of the matrix
On solving above equations we get 
Q11) Find out the Eigen values and Eigen vectors of 
?
A11)
The Characteristics equation is given by 
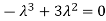
Or 
Hence the Eigen values are 0,0 and 3.
The Eigen vector corresponding to Eigen value 
is
Where X is the column matrix of order 3 i.e.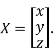
This implies that 
Here number of unknowns are 3 and number of equation is 1.
Hence we have (3-1) = 2 linearly independent solutions.
Let 
Thus the Eigen vectors corresponding to the Eigen value 
are (-1,1,0) and (-2,1,1).
The Eigen vector corresponding to Eigen value 
is
Where X is the column matrix of order 3 i.e.
This implies that 
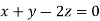
Taking last two equations we get
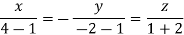
Or 
Thus the Eigen vectors corresponding to the Eigen value 
are (3,3,3).
Hence the three Eigen vectors obtained are (-1,1,0), (-2,1,1) and (3,3,3).
Q12) Find out the Eigen values and Eigen vectors of 
A12)
Let A =
The characteristics equation of A is 
.
Or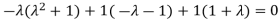 
Or 
Or 
Or 
The Eigen vector corresponding to Eigen value 
is
Where X is the column matrix of order 3 i.e.
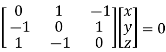
Or 
On solving we get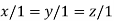 
Thus the Eigen vectors corresponding to the Eigen value 
is (1,1,1).
The Eigen vector corresponding to Eigen value 
is
Where X is the column matrix of order 3 i.e.
Or 
On solving 
or 
.
Thus the Eigen vectors corresponding to the Eigen value 
is (0,0,2).
The Eigen vector corresponding to Eigen value 
is
Where X is the column matrix of order 3 i.e.
Or 
On solving we get 
or 
.
Thus the Eigen vectors corresponding to the Eigen value 
is (2,2,2).
Hence three Eigen vectors are (1,1,1), (0,0,2) and (2,2,2).
Q13) Diagonalise the matrix 
A13)
Let A= 
The three Eigen vectors obtained are (-1,1,0), (-1,0,1) and (3,3,3) corresponding to Eigen values 
.
Then 
and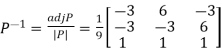 
Also we know that 
Q14) What do you understand by SVD?
A14)
The singular value decomposition of a matrix is usually referred to as the SVD. This is the final and best factorization of a matrix
Where U is orthogonal, Σ is diagonal, and V is orthogonal.
In the decomoposition
A can be any matrix. We know that if A is symmetric positive definite its eigenvectors are orthogonal and we can write A = QΛ
. This is a special case of a SVD, with U = V = Q. For more general A, the SVD requires two different matrices U and V. We’ve also learned how to write A = SΛ
, where S is the matrix of n distinct eigenvectors of A. However, S may not be orthogonal; the matrices U and V in the SVD will be
Q15) Solve the following system of linear equations by using Guass seidel method-
6x + y + z = 105
4x + 8y + 3z = 155
5x + 4y - 10z = 65
A15)
The above equations can be written as,
………………(1)
………………………(2)
………………………..(3)
Now put z = y = 0 in first eq.
We get
x = 35/2
Put x = 35/2 and z = 0 in eq. (2)
We have,
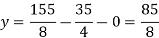
Put the values of x and y in eq. 3
Again start from eq.(1)
By putting the values of y and z
y = 85/8 and z = 13/2
We get
The process can be showed in the table format as below
At the fourth iteration, we get the values of x = 14.98, y = 9.98 , z = 4.98
Unit - 2
Unit - 2
Linear algebra
Q1) Define vector space.
A1)
We define a vector space V where K is the field of scalars as follows-
Let V be a nonempty set with two operations-
(i) Vector Addition: This assigns to any u; v 
V a sum u + v in V.
(ii) Scalar Multiplication: This assigns to any u 
V, k 
K a product ku 
V.
Then V is called a vector space (over the field K) if the following axioms hold for any vectors u; v; w 
V:
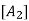There is a vector in V, denoted by 0 and called the zero vector, such that, for any u 
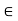V;
For each u 
V; there is a vector in V, denoted by -u, and called the negative of u, such that
u + (-u) (-u) + u = 0
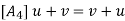
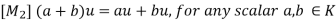
Q2) Define vector.
A2)
An ordered n – touple of numbers is called an n – vector. Thus the ‘n’ numbers x1, x2, …………xn taken in order denote the vector x. i.e. x = (x1, x2, ……., xn).
Where the numbers x1, x2, ………..,xn are called component or co – ordinates of a vector x. A vector may be written as row vector or a column vector.
Q3) What is linear independence?
A3)
A set of r vectors x1, x2, ………….,xr is said to be linearly independent if there exist scalars k1, k2, …………, kr all zero such that
x1 k1 + x2 k2 + …….. + xrkr = 0
Q4) Define linear combination.
A4)
A vector x can be written in the form.
x = x1 k1 + x2 k2 + ……….+xrkr
Where k1, k2, ………….., kr are scalars, then X is called linear combination of x1, x2, ……, xr.
Q5) What is linear span?
A5)
Suppose 
are any vectors in a vector space V. Recall that any vector of the form 
, where the ai are scalars, is called a linear combination of 
.
The collection of all such linear combinations, denoted by Span(
or span(
Clearly the zero vector 0 belongs to span
, because
0 = 0u1 + 0u2 + . . . + 0um
Furthermore, suppose v and v’ belong to span
,, say,
v = a1u1 + a2u2 + . . . + amum and v’ =b1u1 + b2u2 + . . . + bmum
Then
v + v’ = (a1 + b1)u1 + (a2 + b2)u2 + . . . + (am + bm)um
And, for any scalar k belongs to K,
Kv = ka1u1 + ka2u2 + . . . + kamum
Thus, v + v’ and kv also belong to span
. Accordingly, span
is a subspace of V.
Q6) Are the vectors x1 = [1, -3, 4, 2],x2 = [3, -5, 2,6], x3 =[2, -1, 3, 4] linearly dependent. If so, express x1 as a linear combination of the others.
A6)
Consider a vector equation,
x1k1 + x2k2 + x3k3 = 0
i.e., [1, -3, 4, 2]k1 + [3, -5, 2,6]k2 + [2, -1, 3, 4]k3 = [0, 0, 0, 0]
∴ k1 +3k2 + 2k3 = 0
+3k1 + 5k2 + k3 = 0
4k1 + 2k2 + 3k3 = 0
2k1 + 6k2 + 4k3 =0
Which can be written in matrix form as,
R2 + 3R1, R3 – 4R1, R4 – 2R1
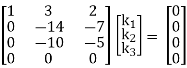
1/14 R2
R3 + 10R2
Here ρ(A) = 2 & no. Of unknown 3. Hence the system has infinite solutions. Now rewrite the questions as,
k1 + 3k2 + 2k3 =0
k2 + ½ k3 =0
Put k3 =t
k2 = -1/2 t and
k1 = -3k2 – 2k3
= - 3 (- ½ t) -2t
= 3/2 t – 2t
= - t/2
Thus k1 = - t/2, k2 = -1/2 t – k3 = t ∀ t ∈ R
i.e., - t/2 × 1 + ( - t/2) x2 + t × 3 = 0
i.e.,- x1/2 – (-x2/2) + x3 = 0
- x1 – x2 + 2 x3 = 0
x1 = - x2 + 2 x3
Since F11k2, k3 not all zero. Hence x1, x2, x3 are linearly dependent.
Q7) At what value of P the following vectors are linearly independent.
[1, 3, 2], [2, P+7, 4], [1, 3, P+3]
A7)
Consider the vector equation.
[1, 3, 2]k1 + [2, P+7, 4]k2 + [1, 3, P+3]k3 = 0
i.e.
k1 + 2k2 + k3 = 0
3k1 + (p + 7)k2 + 3k3 = 0
2k1 + 4k2 + (P +3)k3 = 0
This is a homogeneous system of three equations in 3 unknowns and has a unique trivial solution.
If and only if Determinant of coefficient matrix is non zero.
consider 
.
i.e.,
1[(P + λ)(P+3) – 12] – 2[3(P+3) – 6] + 1[12 – (2P + 14)] 
0
P2 + 10P + 21 – 12 -6P – 6 – 2P – 2 
P2 + 2P + 1 
(P + 1)2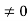 
(P + 1) 
P 
Thus for 
the system has only trivial solution and Hence the vectors are linearly independent.
Q8) What is characteristic equation?
A8)
Let A he a square matrix, λ be any scalar then |A – λI| = 0 is called characteristic equation of a matrix A.
Note:
Let a be a square matrix and ‘λ’ be any scalar then,
1) [A – λI] is called characteristic matrix
2) | A – λI| is called characteristic polynomial.
The roots of a characteristic equations are known as characteristic root or latent roots, Eigen values or proper values of a matrix A.
Q9) What is Eigne vector?
A9)
Suppose λ1 be an Eigen value of a matrix A. Then ∃ a non – zero vector x1 such that.
[A – λI] x1 = 0 ...(1)
Such a vector ‘x1’ is called as Eigen vector corresponding to the Eigen value λ1
Q10) Find the sum and the product of the Eigen values of 
?
A10)
The sum of Eigen values = the sum of the diagonal elements
=1+(-1)=0
The product of the Eigen values is the determinant of the matrix
On solving above equations we get 
Q11) Find out the Eigen values and Eigen vectors of 
?
A11)
The Characteristics equation is given by 
Or 
Hence the Eigen values are 0,0 and 3.
The Eigen vector corresponding to Eigen value 
is
Where X is the column matrix of order 3 i.e.
This implies that 
Here number of unknowns are 3 and number of equation is 1.
Hence we have (3-1) = 2 linearly independent solutions.
Let 
Thus the Eigen vectors corresponding to the Eigen value 
are (-1,1,0) and (-2,1,1).
The Eigen vector corresponding to Eigen value 
is
Where X is the column matrix of order 3 i.e.
This implies that 
Taking last two equations we get
Or 
Thus the Eigen vectors corresponding to the Eigen value 
are (3,3,3).
Hence the three Eigen vectors obtained are (-1,1,0), (-2,1,1) and (3,3,3).
Q12) Find out the Eigen values and Eigen vectors of 
A12)
Let A =
The characteristics equation of A is 
.
Or 
Or 
Or 
Or 
The Eigen vector corresponding to Eigen value 
is
Where X is the column matrix of order 3 i.e.
Or 
On solving we get 
Thus the Eigen vectors corresponding to the Eigen value 
is (1,1,1).
The Eigen vector corresponding to Eigen value 
is
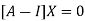
Where X is the column matrix of order 3 i.e.
Or 
On solving 
or 
.
Thus the Eigen vectors corresponding to the Eigen value 
is (0,0,2).
The Eigen vector corresponding to Eigen value 
is
Where X is the column matrix of order 3 i.e.
Or 
On solving we get 
or 
.
Thus the Eigen vectors corresponding to the Eigen value 
is (2,2,2).
Hence three Eigen vectors are (1,1,1), (0,0,2) and (2,2,2).
Q13) Diagonalise the matrix 
A13)
Let A= 
The three Eigen vectors obtained are (-1,1,0), (-1,0,1) and (3,3,3) corresponding to Eigen values 
.
Then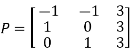 
and 
Also we know that 
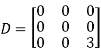
Q14) What do you understand by SVD?
A14)
The singular value decomposition of a matrix is usually referred to as the SVD. This is the final and best factorization of a matrix
Where U is orthogonal, Σ is diagonal, and V is orthogonal.
In the decomoposition
A can be any matrix. We know that if A is symmetric positive definite its eigenvectors are orthogonal and we can write A = QΛ
. This is a special case of a SVD, with U = V = Q. For more general A, the SVD requires two different matrices U and V. We’ve also learned how to write A = SΛ
, where S is the matrix of n distinct eigenvectors of A. However, S may not be orthogonal; the matrices U and V in the SVD will be
Q15) Solve the following system of linear equations by using Guass seidel method-
6x + y + z = 105
4x + 8y + 3z = 155
5x + 4y - 10z = 65
A15)
The above equations can be written as,
………………(1)
………………………(2)
………………………..(3)
Now put z = y = 0 in first eq.
We get
x = 35/2
Put x = 35/2 and z = 0 in eq. (2)
We have,
Put the values of x and y in eq. 3
Again start from eq.(1)
By putting the values of y and z
y = 85/8 and z = 13/2
We get
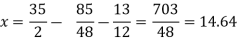
The process can be showed in the table format as below
At the fourth iteration, we get the values of x = 14.98, y = 9.98 , z = 4.98
Unit - 2
Linear algebra
Q1) Define vector space.
A1)
We define a vector space V where K is the field of scalars as follows-
Let V be a nonempty set with two operations-
(i) Vector Addition: This assigns to any u; v 
V a sum u + v in V.
(ii) Scalar Multiplication: This assigns to any u 
V, k 
K a product ku 
V.
Then V is called a vector space (over the field K) if the following axioms hold for any vectors u; v; w 
V:
There is a vector in V, denoted by 0 and called the zero vector, such that, for any u 
V;
For each u 
V; there is a vector in V, denoted by -u, and called the negative of u, such that
u + (-u) (-u) + u = 0
Q2) Define vector.
A2)
An ordered n – touple of numbers is called an n – vector. Thus the ‘n’ numbers x1, x2, …………xn taken in order denote the vector x. i.e. x = (x1, x2, ……., xn).
Where the numbers x1, x2, ………..,xn are called component or co – ordinates of a vector x. A vector may be written as row vector or a column vector.
Q3) What is linear independence?
A3)
A set of r vectors x1, x2, ………….,xr is said to be linearly independent if there exist scalars k1, k2, …………, kr all zero such that
x1 k1 + x2 k2 + …….. + xrkr = 0
Q4) Define linear combination.
A4)
A vector x can be written in the form.
x = x1 k1 + x2 k2 + ……….+xrkr
Where k1, k2, ………….., kr are scalars, then X is called linear combination of x1, x2, ……, xr.
Q5) What is linear span?
A5)
Suppose 
are any vectors in a vector space V. Recall that any vector of the form 
, where the ai are scalars, is called a linear combination of 
.
The collection of all such linear combinations, denoted by Span(
or span(
Clearly the zero vector 0 belongs to span
, because
0 = 0u1 + 0u2 + . . . + 0um
Furthermore, suppose v and v’ belong to span
,, say,
v = a1u1 + a2u2 + . . . + amum and v’ =b1u1 + b2u2 + . . . + bmum
Then
v + v’ = (a1 + b1)u1 + (a2 + b2)u2 + . . . + (am + bm)um
And, for any scalar k belongs to K,
Kv = ka1u1 + ka2u2 + . . . + kamum
Thus, v + v’ and kv also belong to span
. Accordingly, span
is a subspace of V.
Q6) Are the vectors x1 = [1, -3, 4, 2],x2 = [3, -5, 2,6], x3 =[2, -1, 3, 4] linearly dependent. If so, express x1 as a linear combination of the others.
A6)
Consider a vector equation,
x1k1 + x2k2 + x3k3 = 0
i.e., [1, -3, 4, 2]k1 + [3, -5, 2,6]k2 + [2, -1, 3, 4]k3 = [0, 0, 0, 0]
∴ k1 +3k2 + 2k3 = 0
+3k1 + 5k2 + k3 = 0
4k1 + 2k2 + 3k3 = 0
2k1 + 6k2 + 4k3 =0
Which can be written in matrix form as,
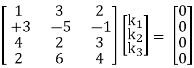
R2 + 3R1, R3 – 4R1, R4 – 2R1
1/14 R2
R3 + 10R2
Here ρ(A) = 2 & no. Of unknown 3. Hence the system has infinite solutions. Now rewrite the questions as,
k1 + 3k2 + 2k3 =0
k2 + ½ k3 =0
Put k3 =t
k2 = -1/2 t and
k1 = -3k2 – 2k3
= - 3 (- ½ t) -2t
= 3/2 t – 2t
= - t/2
Thus k1 = - t/2, k2 = -1/2 t – k3 = t ∀ t ∈ R
i.e., - t/2 × 1 + ( - t/2) x2 + t × 3 = 0
i.e.,- x1/2 – (-x2/2) + x3 = 0
- x1 – x2 + 2 x3 = 0
x1 = - x2 + 2 x3
Since F11k2, k3 not all zero. Hence x1, x2, x3 are linearly dependent.
Q7) At what value of P the following vectors are linearly independent.
[1, 3, 2], [2, P+7, 4], [1, 3, P+3]
A7)
Consider the vector equation.
[1, 3, 2]k1 + [2, P+7, 4]k2 + [1, 3, P+3]k3 = 0
i.e.
k1 + 2k2 + k3 = 0
3k1 + (p + 7)k2 + 3k3 = 0
2k1 + 4k2 + (P +3)k3 = 0
This is a homogeneous system of three equations in 3 unknowns and has a unique trivial solution.
If and only if Determinant of coefficient matrix is non zero.
consider 
.
i.e.,
1[(P + λ)(P+3) – 12] – 2[3(P+3) – 6] + 1[12 – (2P + 14)] 
0
P2 + 10P + 21 – 12 -6P – 6 – 2P – 2 
P2 + 2P + 1 
(P + 1)2 
(P + 1) 
P 
Thus for 
the system has only trivial solution and Hence the vectors are linearly independent.
Q8) What is characteristic equation?
A8)
Let A he a square matrix, λ be any scalar then |A – λI| = 0 is called characteristic equation of a matrix A.
Note:
Let a be a square matrix and ‘λ’ be any scalar then,
1) [A – λI] is called characteristic matrix
2) | A – λI| is called characteristic polynomial.
The roots of a characteristic equations are known as characteristic root or latent roots, Eigen values or proper values of a matrix A.
Q9) What is Eigne vector?
A9)
Suppose λ1 be an Eigen value of a matrix A. Then ∃ a non – zero vector x1 such that.
[A – λI] x1 = 0 ...(1)
Such a vector ‘x1’ is called as Eigen vector corresponding to the Eigen value λ1
Q10) Find the sum and the product of the Eigen values of 
?
A10)
The sum of Eigen values = the sum of the diagonal elements
=1+(-1)=0
The product of the Eigen values is the determinant of the matrix
On solving above equations we get 
Q11) Find out the Eigen values and Eigen vectors of 
?
A11)
The Characteristics equation is given by 
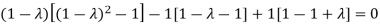
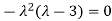
Or 
Hence the Eigen values are 0,0 and 3.
The Eigen vector corresponding to Eigen value 
is
Where X is the column matrix of order 3 i.e.
This implies that 
Here number of unknowns are 3 and number of equation is 1.
Hence we have (3-1) = 2 linearly independent solutions.
Let 
Thus the Eigen vectors corresponding to the Eigen value 
are (-1,1,0) and (-2,1,1).
The Eigen vector corresponding to Eigen value 
is
Where X is the column matrix of order 3 i.e.
This implies that 
Taking last two equations we get
Or 
Thus the Eigen vectors corresponding to the Eigen value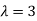 
are (3,3,3).
Hence the three Eigen vectors obtained are (-1,1,0), (-2,1,1) and (3,3,3).
Q12) Find out the Eigen values and Eigen vectors of 
A12)
Let A =
The characteristics equation of A is 
.
Or 
Or 
Or 
Or 
The Eigen vector corresponding to Eigen value 
is
Where X is the column matrix of order 3 i.e.
Or 
On solving we get 
Thus the Eigen vectors corresponding to the Eigen value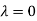 
is (1,1,1).
The Eigen vector corresponding to Eigen value 
is
Where X is the column matrix of order 3 i.e.
Or 
On solving 
or 
.
Thus the Eigen vectors corresponding to the Eigen value 
is (0,0,2).
The Eigen vector corresponding to Eigen value 
is
Where X is the column matrix of order 3 i.e.
Or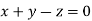 
On solving we get 
or 
.
Thus the Eigen vectors corresponding to the Eigen value 
is (2,2,2).
Hence three Eigen vectors are (1,1,1), (0,0,2) and (2,2,2).
Q13) Diagonalise the matrix 
A13)
Let A= 
The three Eigen vectors obtained are (-1,1,0), (-1,0,1) and (3,3,3) corresponding to Eigen values 
.
Then 
and 
Also we know that 
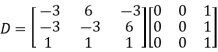
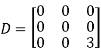
Q14) What do you understand by SVD?
A14)
The singular value decomposition of a matrix is usually referred to as the SVD. This is the final and best factorization of a matrix
Where U is orthogonal, Σ is diagonal, and V is orthogonal.
In the decomoposition
A can be any matrix. We know that if A is symmetric positive definite its eigenvectors are orthogonal and we can write A = QΛ
. This is a special case of a SVD, with U = V = Q. For more general A, the SVD requires two different matrices U and V. We’ve also learned how to write A = SΛ
, where S is the matrix of n distinct eigenvectors of A. However, S may not be orthogonal; the matrices U and V in the SVD will be
Q15) Solve the following system of linear equations by using Guass seidel method-
6x + y + z = 105
4x + 8y + 3z = 155
5x + 4y - 10z = 65
A15)
The above equations can be written as,
………………(1)
………………………(2)
………………………..(3)
Now put z = y = 0 in first eq.
We get
x = 35/2
Put x = 35/2 and z = 0 in eq. (2)
We have,
Put the values of x and y in eq. 3
Again start from eq.(1)
By putting the values of y and z
y = 85/8 and z = 13/2
We get
The process can be showed in the table format as below
At the fourth iteration, we get the values of x = 14.98, y = 9.98 , z = 4.98
