Unit - 3

Mathematical expectations and probability distributions

Q1) Define random variable.

A1)

It is a real valued function which assigns a real number to each sample point in the sample space.

A random variable X is a function defined on the sample space 5 of an experiment S of an experiment. Its value are real numbers. For every number a the probability

With which X assumes a is defined. Similarly for any interval l the probability

With which X assumes any value in I is defined.

Q2) A random variable x has the following probability distribution-

Then find-

1. Value of c.

2. P[X≤3]

3. P[1 < X <4]

A2)

We know that for the given probability distribution-

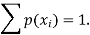
So that-

2.

P[X ≤ 3] = P[X = 3] + P[X = 2] + P[X =1] + P[X = 0]

= 2c + c + c + 0 = 4c = 4 × 1/8 = ½

3.

Q3) Define discrete random variable.

A3)

A random variable is said to be discrete if it has either a finite or a countable number of values. Countable number of values means the values which can be arranged in a sequence.

Note- if a random variable takes a finite set of values it is called discrete and if if a random variable takes an infinite number of uncountable values it is called continuous variable.

Q4) Find the probability distribution of the number of heads when three coins are tossed simultaneously.

A4)

Let be the number of heads in the toss of three coins

The sample space will be-

{HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}

Here variable X can take the values 0, 1, 2, 3 with the following probabilities-

P[X= 0] = P[TTT] = 1/8

P[X = 1] = P [HTT, THH, TTH] = 3/8

P[X = 2] = P[HHT, HTH, THH] = 3/8

P[X = 3] = P[HHH] = 1/8

Hence the probability distribution of X will be-

X
P(x)

Q5) The probability density function of a variable X is

(i)                Find

(ii)             What will be e minimum value of k so that

A5)

(i) If X is a random variable then

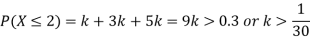
(i)                Thus minimum value of k=1/30.

Q6) Show that the following function can be defined as a density function and then find .

A6)

Here

So that, the function can be defined as a density function.

Now.

Q7) Let X be a continuous random variable with PDF

Find .

A7)

We have

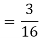
Q8) If a random variable X has the following probability distribution in tabular form then what will be the expected value of X.

A8)

We know that-

So that-

Q9) Find the expectations of the number of an unbiased die when thrown.

Sol. Let X be a random variable which represents the number on a die when thrown.

A9)

X can take the values-

1, 2, 3, 4, 5, 6

With

P[X = 1] = P[X = 2] = P[X = 3] = P[X = 4] = P[X = 5] = P[X = 6] = 1/6

The distribution table will be-

Hence the expectation of number on the die thrown is-

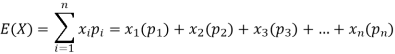
So that-

Q10) Calculate the standard deviation of the following frequency distribution-

A10)

Weight	Item (f)	X	d = x – 67	f.d
60 – 62	5	61	-6	-30	180
63 – 65	18	64	-3	-54	162
66 – 68	42	67	0	0	0
69 – 71	27	70	3	81	243
72 – 74	8	73	6	48	288
Total	100			45	873

Q11) I roll a fair die and let X be the resulting number. Find EX, Var(X), and

A11)

We have   and for k = 1,2,…,6. Thus we have

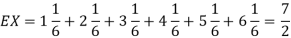
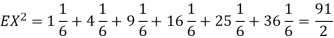
Thus ,

Q12) A die is thrown 8 times then find the probability that 3 will show-

1. Exactly 2 times

2. At least 7 times

3. At least once

A12)

As we know that-

Then-

1. Probability of getting 3 exactly 2 times will be-

2.     Probability of getting 3 at least 7 or 8 times will be-

3.     Probability of getting 3 at least once or (1 or 2 or 3 or 4 or 5 or 6 or 7 or 8 times)-

= P(1) +P(2) +P(3) +P(4) + P(5) + P(6) +P(7) +P(8)

= 1 – P(0) = 1 -

= 1 –

Q13) If the percentage of failure in a test is 20. If six students appear in the test, then what will be the probability that at least five students will pass the test?

A13)

Here

Then the probability of at least five students will pass the test-

= P(5) +P(6) =

Q14) The overall percentage of failures in a certain examination is 20. If 6 candidates appear in the examination what is the probability that at least five pass the examination?

A14)

Probability of failures = 20%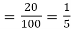

Probability of (P) =

Probability of at least 5 pass = P(5 or 6)

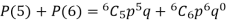
Q15) Assuming that 20% of the population of a city are literate so that the chance of an individual being literate is and assuming that hundred investigators each take 10 individuals to see whether they are illiterate, how many investigators would you expect to report 3 or less were literate.

A15)

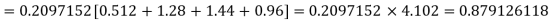
Required number of investigators = 0.879126118× 100 =87.9126118

= 88 approximate

Q16) If cars arriving at workshop follow the Poisson distribution. If the average number of cars arrivals during a specified period of an hour is 2.

Find the probabilities that during the given hour-

1. No car arrive

2. At least two cars arrive.

A16)

Here the average of car arrivals is - 2

So that mean = 2

Let X be the number of cars arriving during the given  hour,

By using Poisson distribution, we get-

So that the required probability-

1. P [no car will arrive] = P [X = x] =

2. P [At least two cars will arrive] = P [X≥2] = P [X =2] + P [X = 3] + ……….

= 1 - P [[X =1] + P [X =0]]

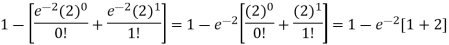
Q17) If a book has 600 pages and it has 40 printing mistakes. Assume that these mistakes are randomly distributed and x the number of mistakes per page follow Poisson distribution.

What is the probability that there will not be any mistake if 10 pages selected at random?

A17)

Here

We get by using Poisson distribution-

Then-

Q18) Find the area under the normal curve in each of the cases

(a)  Z = 0 and z = 1.2

(b)  Z = -0.68 and z = 0

(c)  Z = -0.46 and z = -2.21

(d)  Z = 0.81 and z = 1.94

(e)  To the left of z = -0.6

(f)    Right of z = -1.28

A18)

(a) Area between Z = 0 and z = 1.2 =0.3849

(b)Area between z = 0 and z = -0.68 = 0.2518

(c)Required area = (Area between z = 0 and z = 2.21) + (Area between z = 0 and z =-0.46)\

= (Area between z = 0 and z = 2.21)+ (Area between z = 0 and z = 0.46)

=0.4865 + 0.1772 = 0.6637

(d)Required area = (Area between z = 0 and z = 1.+-(Area between z = 0 and z = 0.81)

= 0.4738-0.2910=0.1828

(e) Required area = 0.5-(Area between z = 0 and z = 0.6)

= 0.5-0.2257=0.2743

(f)Required area = (Area between z = 0 and z = -1.28)+0.5

= 0.3997+0.5

= 0.8997

Q19) A manufacturer knows from experience that the resistance of resistors he produces is normal with mean and standard deviation . What percentage of resistors will have resistance between 98 ohms and 102 ohms?

A19)

,

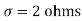
Area between

= (Area between z = 0 and z = +1)

= 2 (Area between z = 0 and z = +1)=2 0.3413 = 0.6826

Percentage of resistors having resistance between 98 ohms and 102 ohms = 68.26

Q20) In a company the mean weight of 1000 employees is 60kg and standard deviation is 16kg.

Find the number of employees having their weights-

1. Less than 55kg.

2. More than 70kg.

3. Between 45kg and 65kg.

A20)

Suppose X be a normal variate = the weight of employees.

Here mean 60kg and S.D. = 16kg

X

Then we know that-

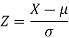
We get from the data,

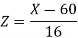
Now-

1. For X = 55,

So that-

P[X < 55] = P[Z < - 0.31] = P[Z > 0.31]

= 0.5 – P[0 < Z < 0.31]

= 0.5 – 0.1217

=0.3783

2. For X = 70,

So that-

P[X > 70] = P[Z > 0.63]

= 0.5 – P[0 < Z < 0.63]

= 0.5 – 0.2357 = 0.2643

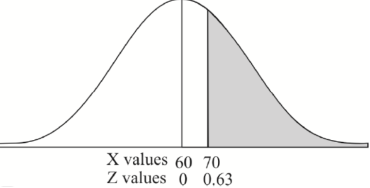
3. For X = 45,

For X = 65,

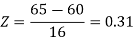
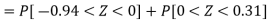
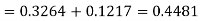
Hence the number of employees having weights between 45kg and 65kg-

Q21) The mean inside diameter of a sample of 200 washers produced by a machine is 0.0502 cm and the standard deviation is 0.005 cm. The purpose for which these washers are intended allows a maximum tolerance in the diameter of 0.496 to 0.508 cm, otherwise the washers are considered defective. Determine the percentage of defective washers produced by the machine, assuming the diameters are normally distributed.

A21)

Here-

And

Area for non-defective washers = area between z = -1.2 to +1.2

= 2 area between z = 0 and z = 1.2

= 2 × 0.3849 = 0.7698 = 76.98%

Then percent of defective washers = 100 – 76.98 = 23.02 %

Unit - 3

Mathematical expectations and probability distributions

Q1) Define random variable.

A1)

It is a real valued function which assigns a real number to each sample point in the sample space.

A random variable X is a function defined on the sample space 5 of an experiment S of an experiment. Its value are real numbers. For every number a the probability

With which X assumes a is defined. Similarly for any interval l the probability

With which X assumes any value in I is defined.

Q2) A random variable x has the following probability distribution-

Then find-

1. Value of c.

2. P[X≤3]

3. P[1 < X <4]

A2)

We know that for the given probability distribution-

So that-

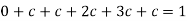
2.

P[X ≤ 3] = P[X = 3] + P[X = 2] + P[X =1] + P[X = 0]

= 2c + c + c + 0 = 4c = 4 × 1/8 = ½

3.

Q3) Define discrete random variable.

A3)

A random variable is said to be discrete if it has either a finite or a countable number of values. Countable number of values means the values which can be arranged in a sequence.

Note- if a random variable takes a finite set of values it is called discrete and if if a random variable takes an infinite number of uncountable values it is called continuous variable.

Q4) Find the probability distribution of the number of heads when three coins are tossed simultaneously.

A4)

Let be the number of heads in the toss of three coins

The sample space will be-

{HHH, HHT, HTH, THH, HTT, THT, TTH, TTT}

Here variable X can take the values 0, 1, 2, 3 with the following probabilities-

P[X= 0] = P[TTT] = 1/8

P[X = 1] = P [HTT, THH, TTH] = 3/8

P[X = 2] = P[HHT, HTH, THH] = 3/8

P[X = 3] = P[HHH] = 1/8

Hence the probability distribution of X will be-

X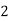
P(x)

Q5) The probability density function of a variable X is

(i)                Find

(ii)             What will be e minimum value of k so that

A5)

(i) If X is a random variable then

(i)                Thus minimum value of k=1/30.

Q6) Show that the following function can be defined as a density function and then find .

A6)

Here

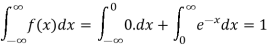
So that, the function can be defined as a density function.

Now.

Q7) Let X be a continuous random variable with PDF

Find .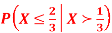

A7)

We have

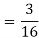
Q8) If a random variable X has the following probability distribution in tabular form then what will be the expected value of X.

A8)

We know that-

So that-

Q9) Find the expectations of the number of an unbiased die when thrown.

Sol. Let X be a random variable which represents the number on a die when thrown.

A9)

X can take the values-

1, 2, 3, 4, 5, 6

With

P[X = 1] = P[X = 2] = P[X = 3] = P[X = 4] = P[X = 5] = P[X = 6] = 1/6

The distribution table will be-

Hence the expectation of number on the die thrown is-

So that-

Q10) Calculate the standard deviation of the following frequency distribution-

A10)

Weight	Item (f)	X	d = x – 67	f.d
60 – 62	5	61	-6	-30	180
63 – 65	18	64	-3	-54	162
66 – 68	42	67	0	0	0
69 – 71	27	70	3	81	243
72 – 74	8	73	6	48	288
Total	100			45	873

Q11) I roll a fair die and let X be the resulting number. Find EX, Var(X), and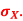

A11)

We have   and for k = 1,2,…,6. Thus we have

Thus ,

Q12) A die is thrown 8 times then find the probability that 3 will show-

1. Exactly 2 times

2. At least 7 times

3. At least once

A12)

As we know that-

Then-

1. Probability of getting 3 exactly 2 times will be-

2.     Probability of getting 3 at least 7 or 8 times will be-

3.     Probability of getting 3 at least once or (1 or 2 or 3 or 4 or 5 or 6 or 7 or 8 times)-

= P(1) +P(2) +P(3) +P(4) + P(5) + P(6) +P(7) +P(8)

= 1 – P(0) = 1 -

= 1 –

Q13) If the percentage of failure in a test is 20. If six students appear in the test, then what will be the probability that at least five students will pass the test?

A13)

Here

Then the probability of at least five students will pass the test-

= P(5) +P(6) =

Q14) The overall percentage of failures in a certain examination is 20. If 6 candidates appear in the examination what is the probability that at least five pass the examination?

A14)

Probability of failures = 20%

Probability of (P) =

Probability of at least 5 pass = P(5 or 6)

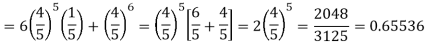
Q15) Assuming that 20% of the population of a city are literate so that the chance of an individual being literate is and assuming that hundred investigators each take 10 individuals to see whether they are illiterate, how many investigators would you expect to report 3 or less were literate.

A15)

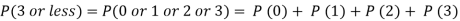
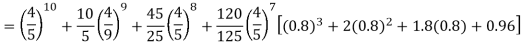
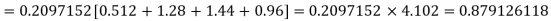
Required number of investigators = 0.879126118× 100 =87.9126118

= 88 approximate

Q16) If cars arriving at workshop follow the Poisson distribution. If the average number of cars arrivals during a specified period of an hour is 2.

Find the probabilities that during the given hour-

1. No car arrive

2. At least two cars arrive.

A16)

Here the average of car arrivals is - 2

So that mean = 2

Let X be the number of cars arriving during the given  hour,

By using Poisson distribution, we get-

So that the required probability-

1. P [no car will arrive] = P [X = x] =

2. P [At least two cars will arrive] = P [X≥2] = P [X =2] + P [X = 3] + ……….

= 1 - P [[X =1] + P [X =0]]

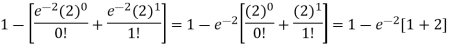
Q17) If a book has 600 pages and it has 40 printing mistakes. Assume that these mistakes are randomly distributed and x the number of mistakes per page follow Poisson distribution.

What is the probability that there will not be any mistake if 10 pages selected at random?

A17)

Here

We get by using Poisson distribution-

Then-

Q18) Find the area under the normal curve in each of the cases

(a)  Z = 0 and z = 1.2

(b)  Z = -0.68 and z = 0

(c)  Z = -0.46 and z = -2.21

(d)  Z = 0.81 and z = 1.94

(e)  To the left of z = -0.6

(f)    Right of z = -1.28

A18)

(a) Area between Z = 0 and z = 1.2 =0.3849

(b)Area between z = 0 and z = -0.68 = 0.2518

(c)Required area = (Area between z = 0 and z = 2.21) + (Area between z = 0 and z =-0.46)\

= (Area between z = 0 and z = 2.21)+ (Area between z = 0 and z = 0.46)

=0.4865 + 0.1772 = 0.6637

(d)Required area = (Area between z = 0 and z = 1.+-(Area between z = 0 and z = 0.81)

= 0.4738-0.2910=0.1828

(e) Required area = 0.5-(Area between z = 0 and z = 0.6)

= 0.5-0.2257=0.2743

(f)Required area = (Area between z = 0 and z = -1.28)+0.5

= 0.3997+0.5

= 0.8997

Q19) A manufacturer knows from experience that the resistance of resistors he produces is normal with mean and standard deviation . What percentage of resistors will have resistance between 98 ohms and 102 ohms?

A19)

,

Area between

= (Area between z = 0 and z = +1)

= 2 (Area between z = 0 and z = +1)=2 0.3413 = 0.6826

Percentage of resistors having resistance between 98 ohms and 102 ohms = 68.26

Q20) In a company the mean weight of 1000 employees is 60kg and standard deviation is 16kg.

Find the number of employees having their weights-

1. Less than 55kg.

2. More than 70kg.

3. Between 45kg and 65kg.

A20)

Suppose X be a normal variate = the weight of employees.

Here mean 60kg and S.D. = 16kg

X

Then we know that-

We get from the data,

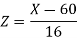
Now-

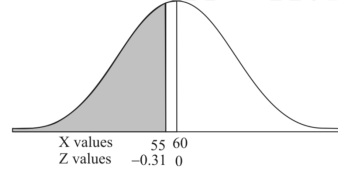
1. For X = 55,

So that-

P[X < 55] = P[Z < - 0.31] = P[Z > 0.31]

= 0.5 – P[0 < Z < 0.31]

= 0.5 – 0.1217

=0.3783

2. For X = 70,

So that-

P[X > 70] = P[Z > 0.63]

= 0.5 – P[0 < Z < 0.63]

= 0.5 – 0.2357 = 0.2643

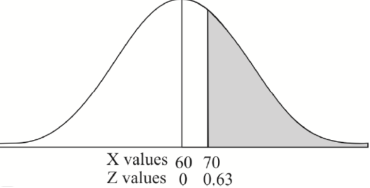
3. For X = 45,

For X = 65,

Hence the number of employees having weights between 45kg and 65kg-

Q21) The mean inside diameter of a sample of 200 washers produced by a machine is 0.0502 cm and the standard deviation is 0.005 cm. The purpose for which these washers are intended allows a maximum tolerance in the diameter of 0.496 to 0.508 cm, otherwise the washers are considered defective. Determine the percentage of defective washers produced by the machine, assuming the diameters are normally distributed.

A21)

Here-

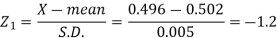
And

Area for non-defective washers = area between z = -1.2 to +1.2

= 2 area between z = 0 and z = 1.2

= 2 × 0.3849 = 0.7698 = 76.98%

Then percent of defective washers = 100 – 76.98 = 23.02 %