Unit - 5
Stochastic process and sampling techniques
Q1) Define stochastic process.
A1)
A stochastic process is a collection of random variables that take values in a set S, the state space.
The collection is indexed by another set T, the index set. The two most common index sets are the natural numbers T = {0, 1, 2, ...}, and the nonnegative real numbers
T = [0,∞), which usually represent discrete time and continuous time, respectively.
The first index set thus gives a sequence of random variables {X0,X1,X2, ...} and the second, a collection of random variables {X(t), t ≥ 0}, one random variable for each time t. In general, the index set does not have to describe time but is also commonly used to describe spatial location. The state space can be finite, countably infinite, or uncountable, depending on the application.
Q2) What is probability vector?
A2)
Probability vector is a vector-

If  for every ‘i’ and
for every ‘i’ and 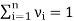
Q3) Define stochastic matrix.
A3)
All the entries of square matrix P are non-negative and the sum of the entries of any row is one.
A vector v is said to be a fixed vector or a fixed point of a matrix A if vA = v and v = 0.
If v is a fixed vector of A, so is kv since
(kv)A = k(vA) = k(v) = kv.
Q4) Which vectors are probability vectors?
- (5/2, 0, 8/3, 1/6, 1/6)
- (3, 0, 2, 5, 3)
A4)
- It is not a probability vector because the sum of the components do not add up to 1
- Dividing by 3 + 0 + 2 + 5 + 3 = 13, we get the probability vector
(3/13, 0, 2/13, 5/13, 3/13)
Q5) Show that  = (b a) is a fixed point of the stochastic matrix-
= (b a) is a fixed point of the stochastic matrix-
P = 
A5)
v P = (b a)
(b – ab + ab ba + a – ab) = (b a) = v
Q6) Find the unique fixed probability vector t of

A6)
Suppose t = (x, y, z) be the fixed probability vector.
By definition x + y + z = 1. So t = (x, y,
1 − x − y), t is said to be fixed vector, if t P = t

On solving, we get-




Required fixed probability vector is-

Q7) Explain Markov chain.
A7)
Let X0,X1,X2, ... Be a sequence of discrete random variables, taking values in some set S and that are such that
P(Xn+1 = j | X0 = i0, . . . , Xn-1 = in-1, Xn = i) = P(Xn+1 = j|Xn = i)
For all i, j, i0, ..., in−1 in S and all n. The sequence {Xn} is then called a Markov chain
We often think of the index n as discrete time and say that Xn is the state of the chain at time n, where the state space S may be finite or countably infinite. The defining property is called the Markov property, which can be stated in words as “conditioned on the present, the future is independent of the past.” In general, the probability P(Xn+1 = j|Xn = i) depends on i, j, and n. It is, however, often the case (as in our roulette example) that there is no dependence on
n. We call such chains time-homogeneous and restrict our attention to these chains. Since the conditional probability in the definition thus depends only on i and j, we
Use the notation\
pij = P(Xn+1 = j | Xn = j), i, j ∈ S
And call these the transition probabilities of the Markov chain. Thus, if the chain is in state i, the probabilities pij describe how the chain chooses which state to jump to next. Obviously the transition probabilities have to satisfy the following two criteria:
(a) pij ≥ 0, for all I, j ∈ S, (b) 
Q8) What is random walk?
A8)
Many of the examples we looked at in the previous section are similar in nature.
For example, the roulette example and the various versions of gambler’s ruin have in common that the states are integers and the only possible transitions are one step up or one step down. We now take a more systematic look at such Markov chains, called simple random walks. A simple random walk can be described as a Markov chain {Sn} that is such that

Where the Xk are i.i.d. Such that P(Xk = 1) = p, P(Xk = −1) = 1 − p.
The term “simple” refers to the fact that only unit steps are possible; more generally we could let the Xk have any distribution on the integers. The initial state S0 is usually fixed but could also be chosen according to some probability distribution.
Unless otherwise mentioned, we will always have S0 ≡ 0. If p = 1/2 , the walk is said to be symmetric. It is clear from the construction that the random walk is a Markov chain with state space S = {...,−2,−1, 0, 1, 2, ...} and transition graph

Note how the transition probabilities pi,i+1 and pi,i−1 do not depend on i, a property called spatial homogeneity. We can also illustrate the random walk as a function of time, as was done in Example 1.6.16. Note that this illustrates one particular outcome of the sequence S0, S1, S2, ..., called a sample path, or a realization, of the random walk.
It is clear that the random walk is irreducible, so it has to be either transient, null recurrent, or positive recurrent, and which one it is may depend on p. The random walk is a Markov chain where we can compute the n-step transition probabilities explicitly
pij(2n – 1) = 0 , n = 1, 2, . . .
Since we cannot make it back to a state in an odd number of steps. To make it back in 2n steps, we must take n steps up and n steps down, which has probability

And since convergence of the sum of the  is not affected by the values of any finite number of terms in the beginning, we can use an asymptotic approximation of n!, Stirling’s formula, which says that
is not affected by the values of any finite number of terms in the beginning, we can use an asymptotic approximation of n!, Stirling’s formula, which says that
n! ~ nn √ne-n √2π
Where “∼” means that the ratio of the two sides goes to 1 as n → ∞. The practical use is that we can substitute one for the other for large n in the sum in
Pii(2n) ~ (4p(1 – p))n/ √πn
And if p = 1/2, this equals 1/√πn and the sum over n is infinite.
Q9) What is sample mean and variance?
A9)
Let  be a random sample of size n taken from a population whose pmf or pdf function f(x,
be a random sample of size n taken from a population whose pmf or pdf function f(x, 
Then the sample mean is defined by-

And sample variance-

Q10) A company of pens claims that a certain pen manufactured by him has a mean writing-life at least 460 A-4 size pages. A purchasing agent selects a sample of 100 pens and put them on the test. The mean writing-life of the sample found 453 A-4 size pages with standard deviation 25 A-4 size pages. Should the purchasing agent reject the manufacturer’s claim at 1% level of significance?
A10)
It is given that-
Specified value of population mean = 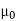 = 460,
= 460,
Sample size = 100
Sample mean = 453
Sample standard deviation = S = 25

The null and alternative hypothesis will be-
H0 : μ ≥ μ0 = 460 and H1 : μ < 460
Also the alternative hypothesis left-tailed so that the test is left tailed test.
Here, we want to test the hypothesis regarding population mean when population SD is unknown. So we should used t-test for if writing-life of pen follows normal distribution. But it is not the case. Since sample size is n = 100 (n > 30) large so we go for Z-test. The test statistic of Z-test is given by


We get the critical value of left tailed Z test at 1% level of significance is 
Since calculated value of test statistic Z (= ‒2.8) is less than the critical value
(= −2.33), that means calculated value of test statistic Z lies in rejection region so we reject the null hypothesis. Since the null hypothesis is the claim so we reject the manufacturer’s claim at 1% level of significance.
Q11) A big company uses thousands of CFL lights every year. The brand that the company has been using in the past has average life of 1200 hours. A new brand is offered to the company at a price lower than they are paying for the old brand. Consequently, a sample of 100 CFL light of new brand is tested which yields an average life of 1220 hours with standard deviation 90 hours. Should the company accept the new brand at 5% level of significance?
A11)
Here we have-

The company may accept the new CFL light when average life of
CFL light is greater than 1200 hours. So the company wants to test that the new brand CFL light has an average life greater than 1200 hours. So our claim is 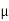 > 1200 and its complement is
> 1200 and its complement is  ≤ 1200. Since complement contains the equality sign so we can take the complement as the null hypothesis and the claim as the alternative hypothesis. Thus,
≤ 1200. Since complement contains the equality sign so we can take the complement as the null hypothesis and the claim as the alternative hypothesis. Thus,

Since the alternative hypothesis is right-tailed so the test is right-tailed test.
Here, we want to test the hypothesis regarding population mean when population SD is unknown, so we should use t-test if the distribution of life of bulbs known to be normal. But it is not the case. Since the sample size is large (n > 30) so we can go for Z-test instead of t-test.
Therefore, test statistic is given by

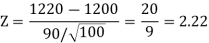
The critical values for right-tailed test at 5% level of significance is
 1.645
1.645
Since calculated value of test statistic Z (= 2.22) is greater than critical value (= 1.645), that means it lies in rejection region so we reject the null hypothesis and support the alternative hypothesis i.e. we support our claim at 5% level of significance
Thus, we conclude that sample does not provide us sufficient evidence against the claim so we may assume that the company accepts the new brand of bulbs
Q12) Eleven students were given a test in statistics. They were given a month’s further tuition and the second test of equal difficulty was held at the end of this. Do the marks give evidence that the students have benefitted by extra coaching?
Boys | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
Marks I test | 23 | 20 | 19 | 21 | 18 | 20 | 18 | 17 | 23 | 16 | 19 |
Marks II test | 24 | 19 | 22 | 18 | 20 | 22 | 20 | 20 | 23 | 20 | 17 |
A12)
We compute the mean and the S.D. Of the difference between the marks of the two tests as under:

Assuming that the students have not been benefitted by extra coaching, it implies that the mean of the difference between the marks of the two tests is zero i.e.
Then,  nearly and df v=11-1=10
nearly and df v=11-1=10
Students |  |  |  |  | 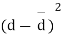 |
1 | 23 | 24 | 1 | 0 | 0 |
2 | 20 | 19 | -1 | -2 | 4 |
3 | 19 | 22 | 3 | 2 | 4 |
4 | 21 | 18 | -3 | -4 | 16 |
5 | 18 | 20 | 2 | 1 | 1 |
6 | 20 | 22 | 2 | 1 | 1 |
7 | 18 | 20 | 2 | 1 | 1 |
8 | 17 | 20 | 3 | 2 | 4 |
9 | 23 | 23 | - | -1 | 1 |
10 | 16 | 20 | 4 | 3 | 9 |
11 | 19 | 17 | -2 | -3 | 9 |
|
|
|  |
|  |
We find that  (for v=10) =2.228. As the calculated value of
(for v=10) =2.228. As the calculated value of  , the value of t is not significant at 5% level of significance i.e. the test provides no evidence that the students have benefitted by extra coaching.
, the value of t is not significant at 5% level of significance i.e. the test provides no evidence that the students have benefitted by extra coaching.
Q13) A college conducts both face to face and distance mode classes for a particular course indented both to be identical. A sample of 50 students of face to face mode yields examination results mean and SD respectively as-

And other sample of 100 distance-mode students yields mean and SD of their examination results in the same course respectively as:

Are both educational methods statistically equal at 5% level?
A13)
Here we have-
n1 = 50  S1 = 12.8
S1 = 12.8
n2 = 100  S2 = 20.5
S2 = 20.5
Here we wish to test that both educational methods are statistically equal. If  denote the average marks of face to face and distance mode students respectively then our claim is
denote the average marks of face to face and distance mode students respectively then our claim is  and its complement is
and its complement is  ≠
≠  . Since the claim contains the equality sign so we can take the claim as the null hypothesis and complement as the alternative hypothesis. Thus,
. Since the claim contains the equality sign so we can take the claim as the null hypothesis and complement as the alternative hypothesis. Thus,

Since the alternative hypothesis is two-tailed so the test is two-tailed test.
We want to test the null hypothesis regarding two population means when standard deviations of both populations are unknown. So we should go for t-test if population of difference is known to be normal. But it is not the case.
Since sample sizes are large (n1, and n2 > 30) so we go for Z-test.
For testing the null hypothesis, the test statistic Z is given by

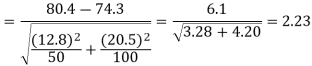
The critical (tabulated) values for two-tailed test at 5% level of significance are-
± zα/2 = ± z0.025 = ± 1.96
Since calculated value of Z ( = 2.23) is greater than the critical values
(= ±1.96), that means it lies in rejection region so we
Reject the null hypothesis i.e. we reject the claim at 5% level of significance
Q14) Define confidence limits.
A14)
Let  be a random sample of size n drawn from a population having pdf (pmf)
be a random sample of size n drawn from a population having pdf (pmf)  .
.
Let  and
and  (here
(here  be two statistic such that the probability that the random interval [
be two statistic such that the probability that the random interval [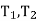 ] including the true value of population parameter
] including the true value of population parameter 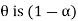 , that is-
, that is-

Here  does not depends on
does not depends on  .
.
Then the random interval [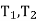 ] is called as (1 –
] is called as (1 –  100 % confidence interval for unknown population parameter
100 % confidence interval for unknown population parameter  and (1 –
and (1 –  is known as confidence coefficient.
is known as confidence coefficient.
The length of interval can be defined as-
Length = Upper confidence – Lower confidence limit
Q15) A tube manufacturer claims that the average life of a particular category of his tube is 18000 km when used under normal driving conditions. A random sample of 16 tube was tested. The mean and SD of life of the tube in the sample were 20000 km and 6000 km respectively.
Assuming that the life of the tube is normally distributed, test the claim of the manufacturer at 1% level of significance using appropriate test.
A15)
Here we have-

We want to test that manufacturer’s claim is true that the average life ( ) of tube is 18000 km. So claim is μ = 18000 and its complement is μ ≠ 18000. Since the claim contains the equality sign so we can take the claim as the null hypothesis and complement as the alternative hypothesis. Thus,
) of tube is 18000 km. So claim is μ = 18000 and its complement is μ ≠ 18000. Since the claim contains the equality sign so we can take the claim as the null hypothesis and complement as the alternative hypothesis. Thus,


Here, population SD is unknown and population under study is given to be normal.
So here can use t-test-
For testing the null hypothesis, the test statistic t is given by-

The critical value of test statistic t for two-tailed test corresponding (n-1) = 15 df at 1% level of significance are 
Since calculated value of test statistic t (= 1.33) is less than the critical (tabulated) value (= 2.947) and greater that critical value (= − 2.947), that means calculated value of test statistic lies in non-rejection region, so we do not reject the null hypothesis. We conclude that sample fails to provide sufficient evidence against the claim so we may assume that manufacturer’s claim is true.
Q16) Two sources of raw materials are under consideration by a bulb manufacturing company. Both sources seem to have similar characteristics but the company is not sure about their respective uniformity. A sample of 12 lots from source A yields a variance of 125 and a sample of 10 lots from source B yields a variance of 112. Is it likely that the variance of source A significantly differs to the variance of source B at significance level α = 0.01?
A16)

The null and alternative hypothesis will be-

Since the alternative hypothesis is two-tailed so the test is two-tailed test.
Here, we want to test the hypothesis about two population variances and sample sizes  = 12(< 30) and
= 12(< 30) and  = 10 (< 30) are small. Also populations under study are normal and both samples are independent.
= 10 (< 30) are small. Also populations under study are normal and both samples are independent.
So we can go for F-test for two population variances.
Test statistic is-


The critical (tabulated) value of test statistic F for two-tailed test corresponding  = (11, 9) df at 5% level of significance are
= (11, 9) df at 5% level of significance are  and
and

Since calculated value of test statistic (= 1.11) is less than the critical value (= 3.91) and greater than the critical value (= 0.28), that means calculated value of test statistic lies in non-rejection region, so we do not reject the null hypothesis and reject the alternative hypothesis. We conclude that samples provide us sufficient evidence against the claim so we may assume that the variances of source A and B is differ.
Q17) In experiments of pea breeding, the following frequencies of seeds were obtained
Round and yellow | Wrinkled and yellow | Round and green | Wrinkled and green | Total |
316 | 101 | 108 | 32 | 556 |
Theory predicts that the frequencies should be in proportions 9:3:3:1. Examine the correspondence between theory and experiment.
A17)
The corresponding frequencies are

Hence,


For v = 3, we have 
Since the calculated value of  is much less than
is much less than  there is a very high degree of agreement between theory and experiment.
there is a very high degree of agreement between theory and experiment.
Unit - 5
Stochastic process and sampling techniques
Q1) Define stochastic process.
A1)
A stochastic process is a collection of random variables that take values in a set S, the state space.
The collection is indexed by another set T, the index set. The two most common index sets are the natural numbers T = {0, 1, 2, ...}, and the nonnegative real numbers
T = [0,∞), which usually represent discrete time and continuous time, respectively.
The first index set thus gives a sequence of random variables {X0,X1,X2, ...} and the second, a collection of random variables {X(t), t ≥ 0}, one random variable for each time t. In general, the index set does not have to describe time but is also commonly used to describe spatial location. The state space can be finite, countably infinite, or uncountable, depending on the application.
Q2) What is probability vector?
A2)
Probability vector is a vector-

If  for every ‘i’ and
for every ‘i’ and 
Q3) Define stochastic matrix.
A3)
All the entries of square matrix P are non-negative and the sum of the entries of any row is one.
A vector v is said to be a fixed vector or a fixed point of a matrix A if vA = v and v = 0.
If v is a fixed vector of A, so is kv since
(kv)A = k(vA) = k(v) = kv.
Q4) Which vectors are probability vectors?
- (5/2, 0, 8/3, 1/6, 1/6)
- (3, 0, 2, 5, 3)
A4)
- It is not a probability vector because the sum of the components do not add up to 1
- Dividing by 3 + 0 + 2 + 5 + 3 = 13, we get the probability vector
(3/13, 0, 2/13, 5/13, 3/13)
Q5) Show that  = (b a) is a fixed point of the stochastic matrix-
= (b a) is a fixed point of the stochastic matrix-
P = 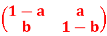
A5)
v P = (b a)
(b – ab + ab ba + a – ab) = (b a) = v
Q6) Find the unique fixed probability vector t of

A6)
Suppose t = (x, y, z) be the fixed probability vector.
By definition x + y + z = 1. So t = (x, y,
1 − x − y), t is said to be fixed vector, if t P = t

On solving, we get-




Required fixed probability vector is-
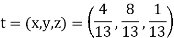
Q7) Explain Markov chain.
A7)
Let X0,X1,X2, ... Be a sequence of discrete random variables, taking values in some set S and that are such that
P(Xn+1 = j | X0 = i0, . . . , Xn-1 = in-1, Xn = i) = P(Xn+1 = j|Xn = i)
For all i, j, i0, ..., in−1 in S and all n. The sequence {Xn} is then called a Markov chain
We often think of the index n as discrete time and say that Xn is the state of the chain at time n, where the state space S may be finite or countably infinite. The defining property is called the Markov property, which can be stated in words as “conditioned on the present, the future is independent of the past.” In general, the probability P(Xn+1 = j|Xn = i) depends on i, j, and n. It is, however, often the case (as in our roulette example) that there is no dependence on
n. We call such chains time-homogeneous and restrict our attention to these chains. Since the conditional probability in the definition thus depends only on i and j, we
Use the notation\
pij = P(Xn+1 = j | Xn = j), i, j ∈ S
And call these the transition probabilities of the Markov chain. Thus, if the chain is in state i, the probabilities pij describe how the chain chooses which state to jump to next. Obviously the transition probabilities have to satisfy the following two criteria:
(a) pij ≥ 0, for all I, j ∈ S, (b) 
Q8) What is random walk?
A8)
Many of the examples we looked at in the previous section are similar in nature.
For example, the roulette example and the various versions of gambler’s ruin have in common that the states are integers and the only possible transitions are one step up or one step down. We now take a more systematic look at such Markov chains, called simple random walks. A simple random walk can be described as a Markov chain {Sn} that is such that

Where the Xk are i.i.d. Such that P(Xk = 1) = p, P(Xk = −1) = 1 − p.
The term “simple” refers to the fact that only unit steps are possible; more generally we could let the Xk have any distribution on the integers. The initial state S0 is usually fixed but could also be chosen according to some probability distribution.
Unless otherwise mentioned, we will always have S0 ≡ 0. If p = 1/2 , the walk is said to be symmetric. It is clear from the construction that the random walk is a Markov chain with state space S = {...,−2,−1, 0, 1, 2, ...} and transition graph

Note how the transition probabilities pi,i+1 and pi,i−1 do not depend on i, a property called spatial homogeneity. We can also illustrate the random walk as a function of time, as was done in Example 1.6.16. Note that this illustrates one particular outcome of the sequence S0, S1, S2, ..., called a sample path, or a realization, of the random walk.
It is clear that the random walk is irreducible, so it has to be either transient, null recurrent, or positive recurrent, and which one it is may depend on p. The random walk is a Markov chain where we can compute the n-step transition probabilities explicitly
pij(2n – 1) = 0 , n = 1, 2, . . .
Since we cannot make it back to a state in an odd number of steps. To make it back in 2n steps, we must take n steps up and n steps down, which has probability

And since convergence of the sum of the  is not affected by the values of any finite number of terms in the beginning, we can use an asymptotic approximation of n!, Stirling’s formula, which says that
is not affected by the values of any finite number of terms in the beginning, we can use an asymptotic approximation of n!, Stirling’s formula, which says that
n! ~ nn √ne-n √2π
Where “∼” means that the ratio of the two sides goes to 1 as n → ∞. The practical use is that we can substitute one for the other for large n in the sum in
Pii(2n) ~ (4p(1 – p))n/ √πn
And if p = 1/2, this equals 1/√πn and the sum over n is infinite.
Q9) What is sample mean and variance?
A9)
Let  be a random sample of size n taken from a population whose pmf or pdf function f(x,
be a random sample of size n taken from a population whose pmf or pdf function f(x, 
Then the sample mean is defined by-

And sample variance-

Q10) A company of pens claims that a certain pen manufactured by him has a mean writing-life at least 460 A-4 size pages. A purchasing agent selects a sample of 100 pens and put them on the test. The mean writing-life of the sample found 453 A-4 size pages with standard deviation 25 A-4 size pages. Should the purchasing agent reject the manufacturer’s claim at 1% level of significance?
A10)
It is given that-
Specified value of population mean =  = 460,
= 460,
Sample size = 100
Sample mean = 453
Sample standard deviation = S = 25

The null and alternative hypothesis will be-
H0 : μ ≥ μ0 = 460 and H1 : μ < 460
Also the alternative hypothesis left-tailed so that the test is left tailed test.
Here, we want to test the hypothesis regarding population mean when population SD is unknown. So we should used t-test for if writing-life of pen follows normal distribution. But it is not the case. Since sample size is n = 100 (n > 30) large so we go for Z-test. The test statistic of Z-test is given by


We get the critical value of left tailed Z test at 1% level of significance is 
Since calculated value of test statistic Z (= ‒2.8) is less than the critical value
(= −2.33), that means calculated value of test statistic Z lies in rejection region so we reject the null hypothesis. Since the null hypothesis is the claim so we reject the manufacturer’s claim at 1% level of significance.
Q11) A big company uses thousands of CFL lights every year. The brand that the company has been using in the past has average life of 1200 hours. A new brand is offered to the company at a price lower than they are paying for the old brand. Consequently, a sample of 100 CFL light of new brand is tested which yields an average life of 1220 hours with standard deviation 90 hours. Should the company accept the new brand at 5% level of significance?
A11)
Here we have-

The company may accept the new CFL light when average life of
CFL light is greater than 1200 hours. So the company wants to test that the new brand CFL light has an average life greater than 1200 hours. So our claim is  > 1200 and its complement is
> 1200 and its complement is 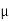 ≤ 1200. Since complement contains the equality sign so we can take the complement as the null hypothesis and the claim as the alternative hypothesis. Thus,
≤ 1200. Since complement contains the equality sign so we can take the complement as the null hypothesis and the claim as the alternative hypothesis. Thus,

Since the alternative hypothesis is right-tailed so the test is right-tailed test.
Here, we want to test the hypothesis regarding population mean when population SD is unknown, so we should use t-test if the distribution of life of bulbs known to be normal. But it is not the case. Since the sample size is large (n > 30) so we can go for Z-test instead of t-test.
Therefore, test statistic is given by


The critical values for right-tailed test at 5% level of significance is
 1.645
1.645
Since calculated value of test statistic Z (= 2.22) is greater than critical value (= 1.645), that means it lies in rejection region so we reject the null hypothesis and support the alternative hypothesis i.e. we support our claim at 5% level of significance
Thus, we conclude that sample does not provide us sufficient evidence against the claim so we may assume that the company accepts the new brand of bulbs
Q12) Eleven students were given a test in statistics. They were given a month’s further tuition and the second test of equal difficulty was held at the end of this. Do the marks give evidence that the students have benefitted by extra coaching?
Boys | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
Marks I test | 23 | 20 | 19 | 21 | 18 | 20 | 18 | 17 | 23 | 16 | 19 |
Marks II test | 24 | 19 | 22 | 18 | 20 | 22 | 20 | 20 | 23 | 20 | 17 |
A12)
We compute the mean and the S.D. Of the difference between the marks of the two tests as under:

Assuming that the students have not been benefitted by extra coaching, it implies that the mean of the difference between the marks of the two tests is zero i.e.
Then,  nearly and df v=11-1=10
nearly and df v=11-1=10
Students |  |  |  |  | 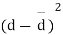 |
1 | 23 | 24 | 1 | 0 | 0 |
2 | 20 | 19 | -1 | -2 | 4 |
3 | 19 | 22 | 3 | 2 | 4 |
4 | 21 | 18 | -3 | -4 | 16 |
5 | 18 | 20 | 2 | 1 | 1 |
6 | 20 | 22 | 2 | 1 | 1 |
7 | 18 | 20 | 2 | 1 | 1 |
8 | 17 | 20 | 3 | 2 | 4 |
9 | 23 | 23 | - | -1 | 1 |
10 | 16 | 20 | 4 | 3 | 9 |
11 | 19 | 17 | -2 | -3 | 9 |
|
|
|  |
|  |
We find that  (for v=10) =2.228. As the calculated value of
(for v=10) =2.228. As the calculated value of  , the value of t is not significant at 5% level of significance i.e. the test provides no evidence that the students have benefitted by extra coaching.
, the value of t is not significant at 5% level of significance i.e. the test provides no evidence that the students have benefitted by extra coaching.
Q13) A college conducts both face to face and distance mode classes for a particular course indented both to be identical. A sample of 50 students of face to face mode yields examination results mean and SD respectively as-

And other sample of 100 distance-mode students yields mean and SD of their examination results in the same course respectively as:

Are both educational methods statistically equal at 5% level?
A13)
Here we have-
n1 = 50  S1 = 12.8
S1 = 12.8
n2 = 100 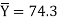 S2 = 20.5
S2 = 20.5
Here we wish to test that both educational methods are statistically equal. If  denote the average marks of face to face and distance mode students respectively then our claim is
denote the average marks of face to face and distance mode students respectively then our claim is  and its complement is
and its complement is  ≠
≠  . Since the claim contains the equality sign so we can take the claim as the null hypothesis and complement as the alternative hypothesis. Thus,
. Since the claim contains the equality sign so we can take the claim as the null hypothesis and complement as the alternative hypothesis. Thus,

Since the alternative hypothesis is two-tailed so the test is two-tailed test.
We want to test the null hypothesis regarding two population means when standard deviations of both populations are unknown. So we should go for t-test if population of difference is known to be normal. But it is not the case.
Since sample sizes are large (n1, and n2 > 30) so we go for Z-test.
For testing the null hypothesis, the test statistic Z is given by


The critical (tabulated) values for two-tailed test at 5% level of significance are-
± zα/2 = ± z0.025 = ± 1.96
Since calculated value of Z ( = 2.23) is greater than the critical values
(= ±1.96), that means it lies in rejection region so we
Reject the null hypothesis i.e. we reject the claim at 5% level of significance
Q14) Define confidence limits.
A14)
Let  be a random sample of size n drawn from a population having pdf (pmf)
be a random sample of size n drawn from a population having pdf (pmf)  .
.
Let  and
and  (here
(here  be two statistic such that the probability that the random interval [
be two statistic such that the probability that the random interval [ ] including the true value of population parameter
] including the true value of population parameter  , that is-
, that is-

Here  does not depends on
does not depends on  .
.
Then the random interval [ ] is called as (1 –
] is called as (1 – 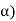 100 % confidence interval for unknown population parameter
100 % confidence interval for unknown population parameter  and (1 –
and (1 –  is known as confidence coefficient.
is known as confidence coefficient.
The length of interval can be defined as-
Length = Upper confidence – Lower confidence limit
Q15) A tube manufacturer claims that the average life of a particular category of his tube is 18000 km when used under normal driving conditions. A random sample of 16 tube was tested. The mean and SD of life of the tube in the sample were 20000 km and 6000 km respectively.
Assuming that the life of the tube is normally distributed, test the claim of the manufacturer at 1% level of significance using appropriate test.
A15)
Here we have-

We want to test that manufacturer’s claim is true that the average life ( ) of tube is 18000 km. So claim is μ = 18000 and its complement is μ ≠ 18000. Since the claim contains the equality sign so we can take the claim as the null hypothesis and complement as the alternative hypothesis. Thus,
) of tube is 18000 km. So claim is μ = 18000 and its complement is μ ≠ 18000. Since the claim contains the equality sign so we can take the claim as the null hypothesis and complement as the alternative hypothesis. Thus,


Here, population SD is unknown and population under study is given to be normal.
So here can use t-test-
For testing the null hypothesis, the test statistic t is given by-

The critical value of test statistic t for two-tailed test corresponding (n-1) = 15 df at 1% level of significance are 
Since calculated value of test statistic t (= 1.33) is less than the critical (tabulated) value (= 2.947) and greater that critical value (= − 2.947), that means calculated value of test statistic lies in non-rejection region, so we do not reject the null hypothesis. We conclude that sample fails to provide sufficient evidence against the claim so we may assume that manufacturer’s claim is true.
Q16) Two sources of raw materials are under consideration by a bulb manufacturing company. Both sources seem to have similar characteristics but the company is not sure about their respective uniformity. A sample of 12 lots from source A yields a variance of 125 and a sample of 10 lots from source B yields a variance of 112. Is it likely that the variance of source A significantly differs to the variance of source B at significance level α = 0.01?
A16)

The null and alternative hypothesis will be-

Since the alternative hypothesis is two-tailed so the test is two-tailed test.
Here, we want to test the hypothesis about two population variances and sample sizes  = 12(< 30) and
= 12(< 30) and  = 10 (< 30) are small. Also populations under study are normal and both samples are independent.
= 10 (< 30) are small. Also populations under study are normal and both samples are independent.
So we can go for F-test for two population variances.
Test statistic is-


The critical (tabulated) value of test statistic F for two-tailed test corresponding  = (11, 9) df at 5% level of significance are
= (11, 9) df at 5% level of significance are  and
and

Since calculated value of test statistic (= 1.11) is less than the critical value (= 3.91) and greater than the critical value (= 0.28), that means calculated value of test statistic lies in non-rejection region, so we do not reject the null hypothesis and reject the alternative hypothesis. We conclude that samples provide us sufficient evidence against the claim so we may assume that the variances of source A and B is differ.
Q17) In experiments of pea breeding, the following frequencies of seeds were obtained
Round and yellow | Wrinkled and yellow | Round and green | Wrinkled and green | Total |
316 | 101 | 108 | 32 | 556 |
Theory predicts that the frequencies should be in proportions 9:3:3:1. Examine the correspondence between theory and experiment.
A17)
The corresponding frequencies are

Hence,


For v = 3, we have 
Since the calculated value of  is much less than
is much less than  there is a very high degree of agreement between theory and experiment.
there is a very high degree of agreement between theory and experiment.