Unit - 2

Regular sets

Q1) What is a regular expression?

A1) Simple expressions called Regular Expressions can readily define the language adopted by finite automata. This is the most powerful way of expressing any language.

●      Regular languages are referred to as the languages recognised by certain regular expressions.

●      A regular expression may also be defined as a pattern sequence that defines a series.

●      For matching character combinations in strings, regular expressions are used. This pattern is used by the string search algorithm to locate operations on a string.

A Regular Expression can be recursively defined as follows -

●      ε is a Regular Expression indicating the language containing an empty string. (L (ε) = {ε})

●      φ is a Regular Expression denoting an empty language. (L (φ) = { })

●      x is a Regular Expression where L = {x}

●      If X is a Regular Expression denoting the language L(X) and Y is a Regular Expression denoting the language L(Y), then

●      X + Y is a Regular Expression corresponding to the language L(X) ∪ L(Y) where L(X+Y) = L(X) ∪ L(Y).

●      X . Y is a Regular Expression corresponding to the language L(X) . L(Y) where L(X.Y) = L(X) . L(Y)

●      R* is a Regular Expression corresponding to the language L(R*)where L(R*) = (L(R))*

Example:

Write the regular expression beginning with a but not including consecutive b's for the language.

Sol: The regular expression has to be create  for the language:

L = {a, aba, aab, aba, aaa, abab, .....}

Q2) Define regular grammar?

A2) If it has rules of form A -> an or A -> aB or A -> ⁇ where ⁇ is a special symbol called NULL, grammar is natural. Standard grammar is formal grammar, i.e. regular right or regular left. Regular language is defined in every periodic grammar

Right linear grammar

Right linear grammar is also called right regular grammar is a formal grammar N, Σ, P, S such that all the production rules in P are of one of the following forms:

1. A → a, where A is a non-terminal in N and a is a terminal in Σ.
2. A → aB, where A and B are non-terminals in N and a is in Σ
3. A → ε, where A is in N and ε denotes the empty string, i.e. the string of length 0.

Left linear grammar

Left linear grammar is also called left regular grammar. There are some rules to follow:

1. A → a, where A in N is a non-terminal and an in Σ is a terminal.
2. A → Ba, where A and B in N are non-terminals and an in Σ is
3. A → ε, where A is N and ε denotes the empty string, i.e. the longitudinal string 0.

Q3) What is the pumping lemma for RE?

A3) Theorem -

Let L be a regular language. Then a constant c' exists such that for every string w in L

|w| ≥ c

We are able to split w into three strings, w=xyz, so that

●      |y| > 0

●      |xy| ≤ c

●      For all k ≥ 0, the string xyKz is also in L.

Application of Pumping Lemma

It is important to apply the Pumping Lemma to show that certain languages are not normal. It can never be used to illustrate the regularity of a language.

●      If L is regular, it satisfies Pumping Lemma.

●      If L does not satisfy Pumping Lemma, it is non-regular.

Method for demonstrating that a language L is not regular

●      We have to assume that L is regular.

●      The pumping lemma should hold for L.

●      Use the pumping lemma to obtain a contradiction −

●      Select w such that |w| ≥ c

●      Select y such that |y| ≥ 1

●      Select x such that |xy| ≤ c

●      Assign the remaining string to z.

●      Select k such that the resulting string is not in L.

Therefore, L is not regular.

Example:

Prove that L = {aibi | i ≥ 0} is not regular.

Sol:

●      At first, we assume that L is regular and n is the number of states.

●      Let w = anbn. Thus |w| = 2n ≥ n.

●      By pumping lemma, let w = xyz, where |xy| ≤ n.

●      Let x = ap , y = aq , and z = arbn , where p + q + r = n, p ≠ 0, q ≠ 0, r ≠ 0. Thus |y| ≠ 0.

●      Let k = 2. Then xy2z = apa2qarbn.

●      Number of as = (p + 2q + r) = (p + q + r) + q = n + q

●      Hence, xy2z = an+q bn . Since q ≠ 0, xy2z is not of the form anbn .

●      Thus, xy2z is not in L.

Hence L is not regular.

Q4) Write the regular expression for the language starting with a but not having consecutive b's?

A4) The regular expression has to be built for the language:

L = {a, aba, aab, aba, aaa, abab, .....} 

The regular expression for the above language is:

R = {a + ab}* 

Q5) What do you mean by the language of RE?

A5) Understand with the examples –

Example 1:

Over the set ∑ = {a}, write the regular expression for the language that accepts all combinations of a's except the null string.

Solution:

The language's regular expression must be created.

L = {a, aa, aaa, ....} 

This set denotes the absence of a null string. As a result, regular expression can be defined as:

R = a+

Example 2:

Write the language's regular expression that accepts any string with any number of a's and b's.

Solution:

The regular expression will look like this:

r.e. = (a + b)* 

The set will be L = {ε, a, aa, b, bb, ab, ba, aba, bab,.....}, any combination of a and b.

Any combination of a and b, including a null string, is represented by the (a + b)*.

Q6) What are regular sets?

A6)

●      A Regular Set is any set that represents the value of a Regular Expression.

●      Sets that are approved by FA are called regular sets (finite automata).

For example:

L = {ε, 11, 1111, 111111, 11111111...}

L stands for a language set with an even number of 1s.

For the above-mentioned language L, finite automata is,

Because we may describe it with finite automata, the given set L is a regular set.

Q7) Write identity rules.

A7)

Given L, M, N as regular expressions, the following identities hold −

1. L + M = M + L
2. (L + M) + N = L + (M + N)
3. (LM)N = L(MN)
4. ∅ + L = L + ∅ = L
5. L = L = L
6. ∅L = L∅ = ∅
7. L(M + N) = LM + LN
8. (M + N)L = ML + NL
9. L + L = L
10. (L ∗ ) ∗ = L ∗
11.  ∅ ∗ = 
12.  ∗ = 
13. (xy) ∗x = x(yx) ∗
14. The following are all equivalent:

(a) (x + y) ∗

(b) (x ∗ + y) ∗

(c) x ∗ (x + y) ∗

(d) (x + yx∗ ) ∗

(e) (x ∗ y ∗ ) ∗

(f) x ∗ (yx∗ ) ∗

(g) (x ∗ y) ∗x ∗

Q8) Write Manipulation rules.

A8)

Associativity law

Let's look at the Regular Expression Associativity Laws.

A + (B + C) = (A + B) + C and A.(B.C) = (A.B).C.

Commutativity for regular expression

Let's look at the Regular Expression Commutativity Laws.

A + B = B + A. However, A.B 6= B.A in general.

Identity for regular expression

Let's look at the Regular Expression Identity.

∅ + A = A + ∅ = A and ε.A = A.ε = A

Distributivity

Let's look at the Regular Expression Distributivity.

Left distributivity: A.(B + C) = A.B + A.C.

Right distributivity:  (B + C).A = B.A + C.A.

Idempotent A + A = A.

Closure laws

Let's look at the Regular Expression Closure laws.

(A*)* = A*, ∅* = ε, ε* = ε, A+ = AA* = A*A, and A* = A + + ε.

DeMorgan Type law

Let's look at the Regular Expression DeMorgan laws.

(L + B)* = (L*B*)*

Q9) What are the closure properties of regular sets?

A9)

Regular sets contain the following characteristics:

Property 1: A regular set is formed by the union of two regular sets.

Proof −

Take a look at two regular expressions.

RE1 = a(aa)* and RE2 = (aa)*

So, L1 = {a, aaa, aaaaa,.....} (Strings of odd length excluding Null)

And L2 ={ ε, aa, aaaa, aaaaaa,.......} (Strings of even length including Null)

L1 ∪ L2 = { ε, a, aa, aaa, aaaa, aaaaa, aaaaaa,.......}

(Strings of all possible lengths including Null)

RE (L1 ∪ L2) = a* (which is a regular expression itself)

Hence proved.

Property 2: It's regular when two regular sets intersect.

Proof -

Take a look at two regular expressions.

RE1 = a(a*) and RE2 = (aa)*

So, L1 = { a,aa, aaa, aaaa, ....} (Strings of all possible lengths excluding Null)

L2 = { ε, aa, aaaa, aaaaaa,.......} (Strings of even length including Null)

L1 ∩ L2 = { aa, aaaa, aaaaaa,.......} (Strings of even length excluding Null)

RE (L1 ∩ L2) = aa(aa)* which is a regular expression itself.

Hence proved.

Property 3: A regular set's complement is also regular.

Proof -

Let's look at an example of a regular expression:

RE = (aa)*

So, L = {ε, aa, aaaa, aaaaaa, .......} (Strings of even length including Null)

L's complement is made up of all strings that aren't in L.

So, L’ = {a, aaa, aaaaa, .....} (Strings of odd length excluding Null)

RE (L’) = a(aa)* which is a regular expression itself.

Hence proved.

Property 4: The difference between two regular sets is regular.

Proof -

Take a look at two regular expressions.

RE1 = a (a*) and RE2 = (aa)*

So, L1 = {a, aa, aaa, aaaa, ....} (Strings of all possible lengths excluding Null)

L2 = { ε, aa, aaaa, aaaaaa,.......} (Strings of even length including Null)

L1 – L2 = {a, aaa, aaaaa, aaaaaaa, ....}

(Strings of all odd lengths excluding Null)

RE (L1 – L2) = a (aa)* which is a regular expression.

Hence proved.

Property 5: A regular set's reversal is also regular.

Proof -

If L is a regular set, we must show that LR is also regular.

Let, L = {01, 10, 11, 10}

RE (L) = 01 + 10 + 11 + 10

LR = {10, 01, 11, 01}

RE (LR) = 01 + 10 + 11 + 10 which is regular

Hence proved.

Property 6: The closure of a regular set is regular.

Proof -

If L = {a, aaa, aaaaa, .......} (Strings of odd length excluding Null)

i.e., RE (L) = a (aa)*

L* = {a, aa, aaa, aaaa , aaaaa,……………} (Strings of all lengths excluding Null)

RE (L*) = a (a)*

Hence proved.

Property 7: The concatenation of two regular sets is regular.

Proof -

Let RE1 = (0+1)*0 and RE2 = 01(0+1)*

Here, L1 = {0, 00, 10, 000, 010, ......} (Set of strings ending in 0)

And L2 = {01, 010,011,.....} (Set of strings beginning with 01)

Then, L1 L2 = {001,0010,0011,0001,00010,00011,1001,10010,.............}

Set of strings containing 001 as a substring which can be represented by an RE − (0 + 1)*001(0 + 1)*

Hence, proved.

Q10) Explain Chomsky hierarchy of languages.

A10)

The Chomsky Hierarchy describes the class of languages that the various machines embrace. The language group in Chomsky's Hierarchy is as follows:

1. Type 0 known as Unrestricted Grammar.
2. Type 1 known as Context Sensitive Grammar.
3. Type 2 known as Context Free Grammar.
4. Type 3 Regular Grammar.

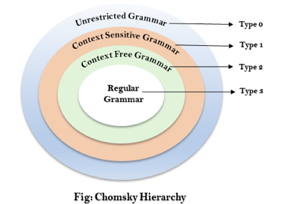
Fig: Chomsky hierarchy

The above diagram shows the hierarchy of chomsky. Each language of type 3 is therefore also of type 2, 1 and 0 respectively. Similarly, every language of type 2 is also of type 1 and type 0 likewise.

●      Type 0 grammar -

Type 0 grammar is known as Unrestricted grammar.The grammar rules of these types of languages are unregulated. Turing machines can model these languages efficiently.

Example:

1. BAa → aa 
2. P → p 

●      Type 1 grammar -

Type 1 grammar is known as Context Sensitive Grammar.Context-sensitive grammar is used to describe language that is sensitive to context. The context-sensitive grammar follows the rules below:

●      There may be more than one symbol on the left side of their development rules for context-sensitive grammar.

●      The number of left-hand symbols does not surpass the number of right-hand symbols.

●      The A → ε type rule is not permitted unless A is a beginning symbol. It does not occur on the right-hand side of any rule.

●      The Type 1 grammar should be Type 0. Production is in the form of V →T in type1

●      Type 2 grammar -

Type 2 Grammar is called Context Free Grammar. Context free languages are the languages which can be represented by the CNF (context free grammar) Type 2 should be type 1. The production rule is:

A → α

●      Type 3 grammar -

Type 3 Grammar is called Regular Grammar. Those languages that can be represented using regular expressions are regular languages. These languages may be NFA or DFA-modeled.

Type3 has to be in the form of -

V → T*V / T*

Example:

A → xy 

Q11) Explain Manipulation of regular expressions.

A11)

Union - R1 | R2 (sometimes written as R1 U R2 or R1 + R2) is a regular expression if R1 and R2 are regular expressions.

L(R1|R2) = L(R1) U L(R2).

Concatenation - R1R2 (sometimes written as R1.R2) is a regular expression if R1 and R2 are regular expressions.

L(R1R2) = L(R1) concatenated with L(R2).

Kleene closure - R1* (the Kleene closure of R1) is a regular expression if R1 is a regular expression.

L(R1*) = epsilon U L(R1) U L(R1R1) U L(R1R1R1) U ...

Closure takes precedence over concatenation, which takes precedence over union.

Example

Over the set ∑ = {a}, write the regular expression for the language that accepts all combinations of a's.

A can be zero, single, double, and so on in any combination of a's. If the letter an appears zero times, the string is null. That is, the set of {ε, a, aa, aaa, ....}. As a result, we can write this as a regular expression:

R = a*

That's how a Kleen closure works.