Unit - 4

Turing Machine

Q1) Explain the turning machine?

A1) An information processing system (TM) may be a mathematical model that consists of associate infinite length tape divided into cells on which input is given. It consists of a head that reads the input tape.

A state register stores the state of the information processing system. Once reading an associated input image, it’s replaced with another image, its internal state is modified, and it moves from one cell to the proper or left. If the metal reaches the ultimate state, the input string is accepted, otherwise rejected.

Formal definition

A metal will be formally delineate as a 7-tuple (Q, X, ∑, δ, q0, B, F)

Where −

• Q may be a finite set of states

• X is that the tape alphabet

• ∑ is that the input alphabet

• δ may be a transition function; δ : alphabetic character × X → alphabetic  character       × X ×

• q0 is that the initial state

• B is that the blank image

• F is that the set of ultimate states

Basic model of turing machine

With the help of the following representation, the turning machine can be modeled.

1. The input tape contains an infinite number of cells, each cell containing one input symbol, so it is possible to position the input string on the tape. Blank characters fill up the empty tape.

Fig 1: Input tape

2.     The finite control and the head of tape that is responsible for reading the current symbol of input. The head of the tape will switch from left to right,

3.     A finite set of states through which the system has to go through.

4.     Finite set of symbols that are used in the construction of the turing machine logic, called external symbols.

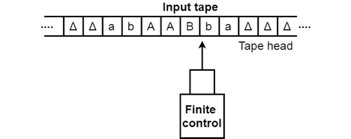
Fig 2: Basic model of TM

Various features of the Turing machine exist:

●      It has an external memory that recalls an arbitrary, long input list.

●      It has infinite capability for memory.

●      The model has a method in which it is easy to read the input on the tape on the left or right.

●      Depending on its input, the computer may generate a certain output. It will often be appropriate for the same input to be used to produce the output. So, the distinction between input and output has been abolished in this machine. It is therefore possible to use a standard set of alphabets for the Turing machine.

Q2) Explain design of turing machine?

A2)

The Turing machine is a mathematical model of a machine that operates mechanically on a tape. There are symbols on this tape that the machine can read and write one at a time with the help of a tape head. The operation is entirely determined by a finite set of elementary instructions such as "write a 1 in state 42 if the symbol seen is 0; change to state 17 if the symbol seen is 1; write a 1 in state 17 if the symbol seen is 0 and change to state 6;" and so on. Turing imagines a person, whom he calls the "computer," who performs these deterministic mechanical laws slavishly in the original essay ("On Computable Numbers, with an Application to the Entscheidungs problem").

Fig 3: The instruction to be performed (q4) is shown over the scanned square

Fig 4: the internal state (q1) is shown inside the head, and the illustration describes the tape as being infinite and pre-filled with "0", the symbol serving as blank.

A Turing machine is made up of the following components:

●      A tape with cells that are stacked one on top of the other. A symbol from a finite alphabet is contained in each cell. A specific blank symbol (here spelled as '0') and one or more other symbols make up the alphabet. The tape is supposed to be extensible to the left and right arbitrarily, ensuring that the Turing machine has access to as much tape as it requires for computing. The blank symbol is supposed to be filled in cells that have not been written in before. In some models, the tape has a specific symbol on the left end, and it extends or is infinitely extensible to the right.

●      A head that can read and write symbols on the tape as well as move the tape left and right one cell at a time. In certain types, the tape is stationary while the head moves.

●      A state register that stores the state of one of a finite number of Turing machines. The special start state with which the state register is initialized is one of them. These states, according to Turing, take the place of the "state of mind" that a person conducting calculations would be in.

●      Given the present state(qi) of the machine and the symbol(aj) it is reading on the tape (symbol now under the head), a finite table of instructions directs the machine to do the following in order (for the 5-tuple models):

○      Either delete or add a symbol (replacing aj with aj1).

○      Move the head (which can take values of 'L' for one step left, 'R' for one step right, or 'N' for staying in the same spot, as indicated by dk).

○      Assume the same or a different condition as directed (go to state qi1).

Q3) What are the variations of TM?

A3) Variation of TM

1. Multiple tracks Alan Turing Machine:

●      A k-tack Alan Turing machine(for some k>0) has k-tracks and one R/W head that reads and writes all of them one by one.

●      A k-track information processing system may be simulated by one track information processing system.

2. Two-way infinite Tape Alan Turing Machine:

●      Infinite tape of two-way infinite tape information processing system is boundless in each direction left and right.

●      Two-way infinite tape information processing system may be simulated by unidirectional infinite {turing|Turing|Alan Alan Turing|Alan Mathison Turing|mathematician} machine(standard Turing machine).

3. Multi-tape Alan Turing Machine:

●      It has multiple tapes and is controlled by one head.

●      The Multi-tape information processing system is completely different from the k-track information processing system however communicative power is the same.

●      Multi-tape information processing system may be simulated by a single-tap information processing system.

4. Multi-tape Multi-head Alan Turing Machine:

●      The multi-tape information processing system has multiple tapes and multiple Heads.

●      Each tape is controlled by a separate head.

●      Multi-Tape Multi-head information processing systems may be simulated by normal information processing systems.

5. Multi-dimensional Tape Alan Turing Machine:

●      It has multi-dimensional tape wherever the head will move any direction that’s left, right, up or down.

●      Multi-dimensional tape information processing system may be simulated by a one-dimensional information processing system.

6. Multi-head Alan Turing Machine:

●      A multi-head information processing system contains 2 or additional heads to scan the symbols on constant tape.

●      In one step all the heads sense the scanned symbols and move or write severally.

●      Multi-head information processing system may be simulated by single head information processing system.

7. Non-deterministic Alan Turing Machine:

●      A non-deterministic information processing system encompasses a single, method of infinite tape.

●      For a given state and input image has at least one option to move (finite range of decisions for consecutive move), every selection has many decisions of path that it’d follow for a given input string.

●      A non-deterministic information processing system is an adored settled information processing system.

Q4) Define linear bounded automata?

A4) A multi-track non-deterministic Turing machine with a tape of some limited finite length is a linear bounded automaton.

Length = function (Length of the initial input string, constant c)

Here,

Memory information ≤ c × Input information

The measurement is limited to the region bounded by constants. There are two special symbols in the input alphabet that act as left end markers and right end markers, indicating that the transitions do not switch either to the left of the left end marker or to the right of the tape's right end marker.

A linear bounded automata can be defined in  8-tuple -

(Q, X, ∑, q0, ML, MR, δ, F)

Where

●      Q is a finite set of states

●      X is the tape alphabet

●      ∑ is the input alphabet

●      q0 is the initial state

●      ML is the left end marker

●      MR is the right end marker where MR ≠ ML

●      δ is a transition function which maps each pair (state) to (state, tape symbol, Constant ‘c’) where c could become 0 or +1 or -1.

●      F is the set of final states.

Fig 5: Linear bounded automata

Q5) Compute function with turing machine?

A5) Being a partial function, a TM transition feature means that there are input pairs for which the transition feature is not defined.

δ(non-halting-state, symbol) = UNDEF

By adding a new dedicated "run forever" state, R:, we can easily compensate for such an omission

δ(R,σ) = (R,σ) ∀ σ ∈ Σ

Simply send a missing transition to this state without tape modification with this addition, i.e.,

δ(non-halting-state, symbol) = (R, symbol)

The easiest computer we can create that runs indefinitely is this:

RunForever = ( {s,h}, Σ, {}, s, {h} )

There are states of beginning and halt, but no transitions, implying that all transitions go to some state of "run forever"

Q6) Write the features of turing machine?

A6) Various features of turing machine

●      It has an external memory that recalls an arbitrary, long input list.

●      It has infinite capability for memory.

●      The model has a method in which it is easy to read the input on the tape on the left or right.

●      Depending on its input, the computer may generate a certain output. It will often be appropriate for the same input to be used to produce the output. So, the distinction between input and output has been abolished in this machine. It is therefore possible to use a standard set of alphabets for the Turing machine.

Q7) Construct TM for the addition function for the unary number system?

A7) The unary number is made up of only one character, i.e. The number 5 can be written in the unary number system as 11111. In this TM, we are going to perform the addition of two unary numbers.

For example

2 + 3

i.e. 11 + 111 = 11111

If you observe this process of addition, you will find the resemblance with string concatenation function.

In this case, we simply replace + by 1 and move ahead right for searching end of the string we will convert last 1 to Δ.

Input: 3+2

The simulation for 111+11Δ can be shown as below:

Move right up to + sign as:

Convert + to 1 and move right as:

Now, move right

Again move right

Now Δ has encountered, so just move left as:

Convert 1 to Δ

Thus the tape now consists of the addition of two unary numbers.

The TM will look like as follows:

Here, we are implementing the function of f(a + b) = c. We assume a and b both are non zero elements.

Q8) Explain Universal Turing Machine.

A8)

The mathematical device similar to a digital computer is the Turing Machine. It was proposed in the 1930s by the mathematician Turing, and has been the most commonly used computer model in the theory of computability and complexity since then.

The model consists of an input relationship between the output that the computer calculates. On the machine's tape, the input is supplied in binary form, and the output consists of the tape content when the machine stops.

Within the Turing Machine, what decides how the contents of the tape shift is a finite state machine (or FSM, also called a finite automaton). The FSM has been the number of states it has and the transitions between them are determined by the number.

The current state and the character read on the tape decide at each step the next state that the FSM will be in the character that the computer will generate on the tape (possibly the one that reads, leaving the contents unchanged), and the direction in which the head travels, left or right.

The problem with Turing Machines is that for each new computation to be performed, for each input output reference, a separate one must be constructed.

This is why we are implementing the idea of a Universal Turing Machine (UTM), which   the definition of a system M is used along with the input on the tape. The UTM will then simulate M on the rest of the content of the input tape to simulate.

A universal turing machine can thus simulate any other machine.

Fig 6: Universal Turing machine

Q9) Explain Computable function.

A9)

Being a partial function, a TM transition feature means that there are input pairs for which the transition feature is not defined.

δ(non-halting-state, symbol) = UNDEF

By adding a new dedicated "run forever" state, R:, we can easily compensate for such an omission

δ(R,σ) = (R,σ) ∀ σ ∈ Σ

Simply send a missing transition to this state without tape modification with this addition, i.e.,

δ(non-halting-state, symbol) = (R, symbol)

The easiest computer we can create that runs indefinitely is this:

RunForever = ( {s,h}, Σ, {}, s, {h} )

There are states of beginning and halt, but no transitions, implying that all transitions go to some state of "run forever"

Q10) Explain Recursive enumerable language.

A10)

The language is called recursively enumerable if any Turing Machine can be created to accept all strings of the specified language.

If L is the set of strings accepted by some TM, then L is recursively enumerable.

Suppose L is a recursive enumerable language.

If w ∈ L then a TM halts in a final state,

If w ∉ L then a TM halts in a non-final state or loops forever.

If L is a recursive language, then

If w ∈ L then a TM halts in a final state,

If w ∉ L then TM halts in a non-final state.

Q11) Prove Recursive Languages are also recursive enumerable.

A11)

Proof: If L is a recursive function, then there is TM, which determines a language member.

M accepts x if x is in language L.

M rejects on x if x is not in language L.

M can recognise the strings in language that are accepted on those strings, according to the definition.

The formal languages that can be decided are recursively enumerable languages ( fully or partially). Recursively enumerable languages are classified as type 0 languages in Chomsky's hierarchy of formal languages. The following are some instances of recursively enumerable languages:

●      Recursive languages

●      Regular languages

●      Context-sensitive languages

●      Context-free languages and many more.

If a recursively enumerable language can be accepted by the Turing machine, it is recursively enumerable (Read More). Recursively enumerable languages are also known as Turing recognisable languages because of this. Please keep in mind that the Turing machine is far more powerful than finite state automata or pushdown automata, as well as many other machines.

Q12) What is Context sensitive language?

A12)

The language that can be defined by context-sensitive grammar is called CSL.

CFLs are used by the compiler in the parsing phase as they define the syntax of a programming language and are used in many editors.

There are four important components in a grammatical description of a language:

1. There is a set of symbols that form the strings of the language being defined. They are called terminal symbols, represented by V t.
2. There is a finite set of variables, called non-terminals. These are represented by V n.
3. One of the variable represents the language being defined; it is called the start symbol. It is represented by S.
4. There are finite set of rules called productions that represent the recursive definition of a language. Each production consists of:

●      A variable that is being defined by the production. This variable is often called the head of the production.

●      The production symbol ->.

●      A string of zero or more terminals and variable.

Q13) What are the Properties of CSL?

A13)

Properties of CSL are:

●      Union, intersection and concatenation of two context-sensitive languages is context-sensitive.

●      Complement of a context-sensitive language is context-sensitive.

Example –

Consider the following CSG.

S → abc/aAbc

Ab → bA

Ac → Bbcc

BB → Bb

AB → aa/aaA

Q14) What is the language generated by CSL?

A14)

S → aAbc

→ abAc

→ abBbcc

→ aBbbcc

→ aaAbbcc

→ aabAbcc

→ aabbAcc

→ aabbBbccc

→ aabBbbccc

→ aaBbbbccc

→ aaabbbccc

The language generated by this grammar is {an bn cn | n≥1}.

Unit - 4

Turing Machine

Q1) Explain the turning machine?

A1) An information processing system (TM) may be a mathematical model that consists of associate infinite length tape divided into cells on which input is given. It consists of a head that reads the input tape.

A state register stores the state of the information processing system. Once reading an associated input image, it’s replaced with another image, its internal state is modified, and it moves from one cell to the proper or left. If the metal reaches the ultimate state, the input string is accepted, otherwise rejected.

Formal definition

A metal will be formally delineate as a 7-tuple (Q, X, ∑, δ, q0, B, F)

Where −

• Q may be a finite set of states

• X is that the tape alphabet

• ∑ is that the input alphabet

• δ may be a transition function; δ : alphabetic character × X → alphabetic  character       × X ×

• q0 is that the initial state

• B is that the blank image

• F is that the set of ultimate states

Basic model of turing machine

With the help of the following representation, the turning machine can be modeled.

1. The input tape contains an infinite number of cells, each cell containing one input symbol, so it is possible to position the input string on the tape. Blank characters fill up the empty tape.

Fig 1: Input tape

2.     The finite control and the head of tape that is responsible for reading the current symbol of input. The head of the tape will switch from left to right,

3.     A finite set of states through which the system has to go through.

4.     Finite set of symbols that are used in the construction of the turing machine logic, called external symbols.

Fig 2: Basic model of TM

Various features of the Turing machine exist:

●      It has an external memory that recalls an arbitrary, long input list.

●      It has infinite capability for memory.

●      The model has a method in which it is easy to read the input on the tape on the left or right.

●      Depending on its input, the computer may generate a certain output. It will often be appropriate for the same input to be used to produce the output. So, the distinction between input and output has been abolished in this machine. It is therefore possible to use a standard set of alphabets for the Turing machine.

Q2) Explain design of turing machine?

A2)

The Turing machine is a mathematical model of a machine that operates mechanically on a tape. There are symbols on this tape that the machine can read and write one at a time with the help of a tape head. The operation is entirely determined by a finite set of elementary instructions such as "write a 1 in state 42 if the symbol seen is 0; change to state 17 if the symbol seen is 1; write a 1 in state 17 if the symbol seen is 0 and change to state 6;" and so on. Turing imagines a person, whom he calls the "computer," who performs these deterministic mechanical laws slavishly in the original essay ("On Computable Numbers, with an Application to the Entscheidungs problem").

Fig 3: The instruction to be performed (q4) is shown over the scanned square

Fig 4: the internal state (q1) is shown inside the head, and the illustration describes the tape as being infinite and pre-filled with "0", the symbol serving as blank.

A Turing machine is made up of the following components:

●      A tape with cells that are stacked one on top of the other. A symbol from a finite alphabet is contained in each cell. A specific blank symbol (here spelled as '0') and one or more other symbols make up the alphabet. The tape is supposed to be extensible to the left and right arbitrarily, ensuring that the Turing machine has access to as much tape as it requires for computing. The blank symbol is supposed to be filled in cells that have not been written in before. In some models, the tape has a specific symbol on the left end, and it extends or is infinitely extensible to the right.

●      A head that can read and write symbols on the tape as well as move the tape left and right one cell at a time. In certain types, the tape is stationary while the head moves.

●      A state register that stores the state of one of a finite number of Turing machines. The special start state with which the state register is initialized is one of them. These states, according to Turing, take the place of the "state of mind" that a person conducting calculations would be in.

●      Given the present state(qi) of the machine and the symbol(aj) it is reading on the tape (symbol now under the head), a finite table of instructions directs the machine to do the following in order (for the 5-tuple models):

○      Either delete or add a symbol (replacing aj with aj1).

○      Move the head (which can take values of 'L' for one step left, 'R' for one step right, or 'N' for staying in the same spot, as indicated by dk).

○      Assume the same or a different condition as directed (go to state qi1).

Q3) What are the variations of TM?

A3) Variation of TM

1. Multiple tracks Alan Turing Machine:

●      A k-tack Alan Turing machine(for some k>0) has k-tracks and one R/W head that reads and writes all of them one by one.

●      A k-track information processing system may be simulated by one track information processing system.

2. Two-way infinite Tape Alan Turing Machine:

●      Infinite tape of two-way infinite tape information processing system is boundless in each direction left and right.

●      Two-way infinite tape information processing system may be simulated by unidirectional infinite {turing|Turing|Alan Alan Turing|Alan Mathison Turing|mathematician} machine(standard Turing machine).

3. Multi-tape Alan Turing Machine:

●      It has multiple tapes and is controlled by one head.

●      The Multi-tape information processing system is completely different from the k-track information processing system however communicative power is the same.

●      Multi-tape information processing system may be simulated by a single-tap information processing system.

4. Multi-tape Multi-head Alan Turing Machine:

●      The multi-tape information processing system has multiple tapes and multiple Heads.

●      Each tape is controlled by a separate head.

●      Multi-Tape Multi-head information processing systems may be simulated by normal information processing systems.

5. Multi-dimensional Tape Alan Turing Machine:

●      It has multi-dimensional tape wherever the head will move any direction that’s left, right, up or down.

●      Multi-dimensional tape information processing system may be simulated by a one-dimensional information processing system.

6. Multi-head Alan Turing Machine:

●      A multi-head information processing system contains 2 or additional heads to scan the symbols on constant tape.

●      In one step all the heads sense the scanned symbols and move or write severally.

●      Multi-head information processing system may be simulated by single head information processing system.

7. Non-deterministic Alan Turing Machine:

●      A non-deterministic information processing system encompasses a single, method of infinite tape.

●      For a given state and input image has at least one option to move (finite range of decisions for consecutive move), every selection has many decisions of path that it’d follow for a given input string.

●      A non-deterministic information processing system is an adored settled information processing system.

Q4) Define linear bounded automata?

A4) A multi-track non-deterministic Turing machine with a tape of some limited finite length is a linear bounded automaton.

Length = function (Length of the initial input string, constant c)

Here,

Memory information ≤ c × Input information

The measurement is limited to the region bounded by constants. There are two special symbols in the input alphabet that act as left end markers and right end markers, indicating that the transitions do not switch either to the left of the left end marker or to the right of the tape's right end marker.

A linear bounded automata can be defined in  8-tuple -

(Q, X, ∑, q0, ML, MR, δ, F)

Where

●      Q is a finite set of states

●      X is the tape alphabet

●      ∑ is the input alphabet

●      q0 is the initial state

●      ML is the left end marker

●      MR is the right end marker where MR ≠ ML

●      δ is a transition function which maps each pair (state) to (state, tape symbol, Constant ‘c’) where c could become 0 or +1 or -1.

●      F is the set of final states.

Fig 5: Linear bounded automata

Q5) Compute function with turing machine?

A5) Being a partial function, a TM transition feature means that there are input pairs for which the transition feature is not defined.

δ(non-halting-state, symbol) = UNDEF

By adding a new dedicated "run forever" state, R:, we can easily compensate for such an omission

δ(R,σ) = (R,σ) ∀ σ ∈ Σ

Simply send a missing transition to this state without tape modification with this addition, i.e.,

δ(non-halting-state, symbol) = (R, symbol)

The easiest computer we can create that runs indefinitely is this:

RunForever = ( {s,h}, Σ, {}, s, {h} )

There are states of beginning and halt, but no transitions, implying that all transitions go to some state of "run forever"

Q6) Write the features of turing machine?

A6) Various features of turing machine

●      It has an external memory that recalls an arbitrary, long input list.

●      It has infinite capability for memory.

●      The model has a method in which it is easy to read the input on the tape on the left or right.

●      Depending on its input, the computer may generate a certain output. It will often be appropriate for the same input to be used to produce the output. So, the distinction between input and output has been abolished in this machine. It is therefore possible to use a standard set of alphabets for the Turing machine.

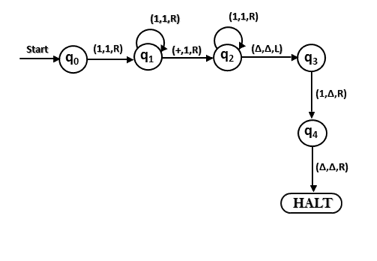
Q7) Construct TM for the addition function for the unary number system?

A7) The unary number is made up of only one character, i.e. The number 5 can be written in the unary number system as 11111. In this TM, we are going to perform the addition of two unary numbers.

For example

2 + 3

i.e. 11 + 111 = 11111

If you observe this process of addition, you will find the resemblance with string concatenation function.

In this case, we simply replace + by 1 and move ahead right for searching end of the string we will convert last 1 to Δ.

Input: 3+2

The simulation for 111+11Δ can be shown as below:

Move right up to + sign as:

Convert + to 1 and move right as:

Now, move right

Again move right

Now Δ has encountered, so just move left as:

Convert 1 to Δ

Thus the tape now consists of the addition of two unary numbers.

The TM will look like as follows:

Here, we are implementing the function of f(a + b) = c. We assume a and b both are non zero elements.

Q8) Explain Universal Turing Machine.

A8)

The mathematical device similar to a digital computer is the Turing Machine. It was proposed in the 1930s by the mathematician Turing, and has been the most commonly used computer model in the theory of computability and complexity since then.

The model consists of an input relationship between the output that the computer calculates. On the machine's tape, the input is supplied in binary form, and the output consists of the tape content when the machine stops.

Within the Turing Machine, what decides how the contents of the tape shift is a finite state machine (or FSM, also called a finite automaton). The FSM has been the number of states it has and the transitions between them are determined by the number.

The current state and the character read on the tape decide at each step the next state that the FSM will be in the character that the computer will generate on the tape (possibly the one that reads, leaving the contents unchanged), and the direction in which the head travels, left or right.

The problem with Turing Machines is that for each new computation to be performed, for each input output reference, a separate one must be constructed.

This is why we are implementing the idea of a Universal Turing Machine (UTM), which   the definition of a system M is used along with the input on the tape. The UTM will then simulate M on the rest of the content of the input tape to simulate.

A universal turing machine can thus simulate any other machine.

Fig 6: Universal Turing machine

Q9) Explain Computable function.

A9)

Being a partial function, a TM transition feature means that there are input pairs for which the transition feature is not defined.

δ(non-halting-state, symbol) = UNDEF

By adding a new dedicated "run forever" state, R:, we can easily compensate for such an omission

δ(R,σ) = (R,σ) ∀ σ ∈ Σ

Simply send a missing transition to this state without tape modification with this addition, i.e.,

δ(non-halting-state, symbol) = (R, symbol)

The easiest computer we can create that runs indefinitely is this:

RunForever = ( {s,h}, Σ, {}, s, {h} )

There are states of beginning and halt, but no transitions, implying that all transitions go to some state of "run forever"

Q10) Explain Recursive enumerable language.

A10)

The language is called recursively enumerable if any Turing Machine can be created to accept all strings of the specified language.

If L is the set of strings accepted by some TM, then L is recursively enumerable.

Suppose L is a recursive enumerable language.

If w ∈ L then a TM halts in a final state,

If w ∉ L then a TM halts in a non-final state or loops forever.

If L is a recursive language, then

If w ∈ L then a TM halts in a final state,

If w ∉ L then TM halts in a non-final state.

Q11) Prove Recursive Languages are also recursive enumerable.

A11)

Proof: If L is a recursive function, then there is TM, which determines a language member.

M accepts x if x is in language L.

M rejects on x if x is not in language L.

M can recognise the strings in language that are accepted on those strings, according to the definition.

The formal languages that can be decided are recursively enumerable languages ( fully or partially). Recursively enumerable languages are classified as type 0 languages in Chomsky's hierarchy of formal languages. The following are some instances of recursively enumerable languages:

●      Recursive languages

●      Regular languages

●      Context-sensitive languages

●      Context-free languages and many more.

If a recursively enumerable language can be accepted by the Turing machine, it is recursively enumerable (Read More). Recursively enumerable languages are also known as Turing recognisable languages because of this. Please keep in mind that the Turing machine is far more powerful than finite state automata or pushdown automata, as well as many other machines.

Q12) What is Context sensitive language?

A12)

The language that can be defined by context-sensitive grammar is called CSL.

CFLs are used by the compiler in the parsing phase as they define the syntax of a programming language and are used in many editors.

There are four important components in a grammatical description of a language:

1. There is a set of symbols that form the strings of the language being defined. They are called terminal symbols, represented by V t.
2. There is a finite set of variables, called non-terminals. These are represented by V n.
3. One of the variable represents the language being defined; it is called the start symbol. It is represented by S.
4. There are finite set of rules called productions that represent the recursive definition of a language. Each production consists of:

●      A variable that is being defined by the production. This variable is often called the head of the production.

●      The production symbol ->.

●      A string of zero or more terminals and variable.

Q13) What are the Properties of CSL?

A13)

Properties of CSL are:

●      Union, intersection and concatenation of two context-sensitive languages is context-sensitive.

●      Complement of a context-sensitive language is context-sensitive.

Example –

Consider the following CSG.

S → abc/aAbc

Ab → bA

Ac → Bbcc

BB → Bb

AB → aa/aaA

Q14) What is the language generated by CSL?

A14)

S → aAbc

→ abAc

→ abBbcc

→ aBbbcc

→ aaAbbcc

→ aabAbcc

→ aabbAcc

→ aabbBbccc

→ aabBbbccc

→ aaBbbbccc

→ aaabbbccc

The language generated by this grammar is {an bn cn | n≥1}.

Unit - 4

Unit - 4

Turing Machine

Q1) Explain the turning machine?

A1) An information processing system (TM) may be a mathematical model that consists of associate infinite length tape divided into cells on which input is given. It consists of a head that reads the input tape.

A state register stores the state of the information processing system. Once reading an associated input image, it’s replaced with another image, its internal state is modified, and it moves from one cell to the proper or left. If the metal reaches the ultimate state, the input string is accepted, otherwise rejected.

Formal definition

A metal will be formally delineate as a 7-tuple (Q, X, ∑, δ, q0, B, F)

Where −

• Q may be a finite set of states

• X is that the tape alphabet

• ∑ is that the input alphabet

• δ may be a transition function; δ : alphabetic character × X → alphabetic  character       × X ×

• q0 is that the initial state

• B is that the blank image

• F is that the set of ultimate states

Basic model of turing machine

With the help of the following representation, the turning machine can be modeled.

1. The input tape contains an infinite number of cells, each cell containing one input symbol, so it is possible to position the input string on the tape. Blank characters fill up the empty tape.

Fig 1: Input tape

2.     The finite control and the head of tape that is responsible for reading the current symbol of input. The head of the tape will switch from left to right,

3.     A finite set of states through which the system has to go through.

4.     Finite set of symbols that are used in the construction of the turing machine logic, called external symbols.

Fig 2: Basic model of TM

Various features of the Turing machine exist:

●      It has an external memory that recalls an arbitrary, long input list.

●      It has infinite capability for memory.

●      The model has a method in which it is easy to read the input on the tape on the left or right.

●      Depending on its input, the computer may generate a certain output. It will often be appropriate for the same input to be used to produce the output. So, the distinction between input and output has been abolished in this machine. It is therefore possible to use a standard set of alphabets for the Turing machine.

Q2) Explain design of turing machine?

A2)

The Turing machine is a mathematical model of a machine that operates mechanically on a tape. There are symbols on this tape that the machine can read and write one at a time with the help of a tape head. The operation is entirely determined by a finite set of elementary instructions such as "write a 1 in state 42 if the symbol seen is 0; change to state 17 if the symbol seen is 1; write a 1 in state 17 if the symbol seen is 0 and change to state 6;" and so on. Turing imagines a person, whom he calls the "computer," who performs these deterministic mechanical laws slavishly in the original essay ("On Computable Numbers, with an Application to the Entscheidungs problem").

Fig 3: The instruction to be performed (q4) is shown over the scanned square

Fig 4: the internal state (q1) is shown inside the head, and the illustration describes the tape as being infinite and pre-filled with "0", the symbol serving as blank.

A Turing machine is made up of the following components:

●      A tape with cells that are stacked one on top of the other. A symbol from a finite alphabet is contained in each cell. A specific blank symbol (here spelled as '0') and one or more other symbols make up the alphabet. The tape is supposed to be extensible to the left and right arbitrarily, ensuring that the Turing machine has access to as much tape as it requires for computing. The blank symbol is supposed to be filled in cells that have not been written in before. In some models, the tape has a specific symbol on the left end, and it extends or is infinitely extensible to the right.

●      A head that can read and write symbols on the tape as well as move the tape left and right one cell at a time. In certain types, the tape is stationary while the head moves.

●      A state register that stores the state of one of a finite number of Turing machines. The special start state with which the state register is initialized is one of them. These states, according to Turing, take the place of the "state of mind" that a person conducting calculations would be in.

●      Given the present state(qi) of the machine and the symbol(aj) it is reading on the tape (symbol now under the head), a finite table of instructions directs the machine to do the following in order (for the 5-tuple models):

○      Either delete or add a symbol (replacing aj with aj1).

○      Move the head (which can take values of 'L' for one step left, 'R' for one step right, or 'N' for staying in the same spot, as indicated by dk).

○      Assume the same or a different condition as directed (go to state qi1).

Q3) What are the variations of TM?

A3) Variation of TM

1. Multiple tracks Alan Turing Machine:

●      A k-tack Alan Turing machine(for some k>0) has k-tracks and one R/W head that reads and writes all of them one by one.

●      A k-track information processing system may be simulated by one track information processing system.

2. Two-way infinite Tape Alan Turing Machine:

●      Infinite tape of two-way infinite tape information processing system is boundless in each direction left and right.

●      Two-way infinite tape information processing system may be simulated by unidirectional infinite {turing|Turing|Alan Alan Turing|Alan Mathison Turing|mathematician} machine(standard Turing machine).

3. Multi-tape Alan Turing Machine:

●      It has multiple tapes and is controlled by one head.

●      The Multi-tape information processing system is completely different from the k-track information processing system however communicative power is the same.

●      Multi-tape information processing system may be simulated by a single-tap information processing system.

4. Multi-tape Multi-head Alan Turing Machine:

●      The multi-tape information processing system has multiple tapes and multiple Heads.

●      Each tape is controlled by a separate head.

●      Multi-Tape Multi-head information processing systems may be simulated by normal information processing systems.

5. Multi-dimensional Tape Alan Turing Machine:

●      It has multi-dimensional tape wherever the head will move any direction that’s left, right, up or down.

●      Multi-dimensional tape information processing system may be simulated by a one-dimensional information processing system.

6. Multi-head Alan Turing Machine:

●      A multi-head information processing system contains 2 or additional heads to scan the symbols on constant tape.

●      In one step all the heads sense the scanned symbols and move or write severally.

●      Multi-head information processing system may be simulated by single head information processing system.

7. Non-deterministic Alan Turing Machine:

●      A non-deterministic information processing system encompasses a single, method of infinite tape.

●      For a given state and input image has at least one option to move (finite range of decisions for consecutive move), every selection has many decisions of path that it’d follow for a given input string.

●      A non-deterministic information processing system is an adored settled information processing system.

Q4) Define linear bounded automata?

A4) A multi-track non-deterministic Turing machine with a tape of some limited finite length is a linear bounded automaton.

Length = function (Length of the initial input string, constant c)

Here,

Memory information ≤ c × Input information

The measurement is limited to the region bounded by constants. There are two special symbols in the input alphabet that act as left end markers and right end markers, indicating that the transitions do not switch either to the left of the left end marker or to the right of the tape's right end marker.

A linear bounded automata can be defined in  8-tuple -

(Q, X, ∑, q0, ML, MR, δ, F)

Where

●      Q is a finite set of states

●      X is the tape alphabet

●      ∑ is the input alphabet

●      q0 is the initial state

●      ML is the left end marker

●      MR is the right end marker where MR ≠ ML

●      δ is a transition function which maps each pair (state) to (state, tape symbol, Constant ‘c’) where c could become 0 or +1 or -1.

●      F is the set of final states.

Fig 5: Linear bounded automata

Q5) Compute function with turing machine?

A5) Being a partial function, a TM transition feature means that there are input pairs for which the transition feature is not defined.

δ(non-halting-state, symbol) = UNDEF

By adding a new dedicated "run forever" state, R:, we can easily compensate for such an omission

δ(R,σ) = (R,σ) ∀ σ ∈ Σ

Simply send a missing transition to this state without tape modification with this addition, i.e.,

δ(non-halting-state, symbol) = (R, symbol)

The easiest computer we can create that runs indefinitely is this:

RunForever = ( {s,h}, Σ, {}, s, {h} )

There are states of beginning and halt, but no transitions, implying that all transitions go to some state of "run forever"

Q6) Write the features of turing machine?

A6) Various features of turing machine

●      It has an external memory that recalls an arbitrary, long input list.

●      It has infinite capability for memory.

●      The model has a method in which it is easy to read the input on the tape on the left or right.

●      Depending on its input, the computer may generate a certain output. It will often be appropriate for the same input to be used to produce the output. So, the distinction between input and output has been abolished in this machine. It is therefore possible to use a standard set of alphabets for the Turing machine.

Q7) Construct TM for the addition function for the unary number system?

A7) The unary number is made up of only one character, i.e. The number 5 can be written in the unary number system as 11111. In this TM, we are going to perform the addition of two unary numbers.

For example

2 + 3

i.e. 11 + 111 = 11111

If you observe this process of addition, you will find the resemblance with string concatenation function.

In this case, we simply replace + by 1 and move ahead right for searching end of the string we will convert last 1 to Δ.

Input: 3+2

The simulation for 111+11Δ can be shown as below:

Move right up to + sign as:

Convert + to 1 and move right as:

Now, move right

Again move right

Now Δ has encountered, so just move left as:

Convert 1 to Δ

Thus the tape now consists of the addition of two unary numbers.

The TM will look like as follows:

Here, we are implementing the function of f(a + b) = c. We assume a and b both are non zero elements.

Q8) Explain Universal Turing Machine.

A8)

The mathematical device similar to a digital computer is the Turing Machine. It was proposed in the 1930s by the mathematician Turing, and has been the most commonly used computer model in the theory of computability and complexity since then.

The model consists of an input relationship between the output that the computer calculates. On the machine's tape, the input is supplied in binary form, and the output consists of the tape content when the machine stops.

Within the Turing Machine, what decides how the contents of the tape shift is a finite state machine (or FSM, also called a finite automaton). The FSM has been the number of states it has and the transitions between them are determined by the number.

The current state and the character read on the tape decide at each step the next state that the FSM will be in the character that the computer will generate on the tape (possibly the one that reads, leaving the contents unchanged), and the direction in which the head travels, left or right.

The problem with Turing Machines is that for each new computation to be performed, for each input output reference, a separate one must be constructed.

This is why we are implementing the idea of a Universal Turing Machine (UTM), which   the definition of a system M is used along with the input on the tape. The UTM will then simulate M on the rest of the content of the input tape to simulate.

A universal turing machine can thus simulate any other machine.

Fig 6: Universal Turing machine

Q9) Explain Computable function.

A9)

Being a partial function, a TM transition feature means that there are input pairs for which the transition feature is not defined.

δ(non-halting-state, symbol) = UNDEF

By adding a new dedicated "run forever" state, R:, we can easily compensate for such an omission

δ(R,σ) = (R,σ) ∀ σ ∈ Σ

Simply send a missing transition to this state without tape modification with this addition, i.e.,

δ(non-halting-state, symbol) = (R, symbol)

The easiest computer we can create that runs indefinitely is this:

RunForever = ( {s,h}, Σ, {}, s, {h} )

There are states of beginning and halt, but no transitions, implying that all transitions go to some state of "run forever"

Q10) Explain Recursive enumerable language.

A10)

The language is called recursively enumerable if any Turing Machine can be created to accept all strings of the specified language.

If L is the set of strings accepted by some TM, then L is recursively enumerable.

Suppose L is a recursive enumerable language.

If w ∈ L then a TM halts in a final state,

If w ∉ L then a TM halts in a non-final state or loops forever.

If L is a recursive language, then

If w ∈ L then a TM halts in a final state,

If w ∉ L then TM halts in a non-final state.

Q11) Prove Recursive Languages are also recursive enumerable.

A11)

Proof: If L is a recursive function, then there is TM, which determines a language member.

M accepts x if x is in language L.

M rejects on x if x is not in language L.

M can recognise the strings in language that are accepted on those strings, according to the definition.

The formal languages that can be decided are recursively enumerable languages ( fully or partially). Recursively enumerable languages are classified as type 0 languages in Chomsky's hierarchy of formal languages. The following are some instances of recursively enumerable languages:

●      Recursive languages

●      Regular languages

●      Context-sensitive languages

●      Context-free languages and many more.

If a recursively enumerable language can be accepted by the Turing machine, it is recursively enumerable (Read More). Recursively enumerable languages are also known as Turing recognisable languages because of this. Please keep in mind that the Turing machine is far more powerful than finite state automata or pushdown automata, as well as many other machines.

Q12) What is Context sensitive language?

A12)

The language that can be defined by context-sensitive grammar is called CSL.

CFLs are used by the compiler in the parsing phase as they define the syntax of a programming language and are used in many editors.

There are four important components in a grammatical description of a language:

1. There is a set of symbols that form the strings of the language being defined. They are called terminal symbols, represented by V t.
2. There is a finite set of variables, called non-terminals. These are represented by V n.
3. One of the variable represents the language being defined; it is called the start symbol. It is represented by S.
4. There are finite set of rules called productions that represent the recursive definition of a language. Each production consists of:

●      A variable that is being defined by the production. This variable is often called the head of the production.

●      The production symbol ->.

●      A string of zero or more terminals and variable.

Q13) What are the Properties of CSL?

A13)

Properties of CSL are:

●      Union, intersection and concatenation of two context-sensitive languages is context-sensitive.

●      Complement of a context-sensitive language is context-sensitive.

Example –

Consider the following CSG.

S → abc/aAbc

Ab → bA

Ac → Bbcc

BB → Bb

AB → aa/aaA

Q14) What is the language generated by CSL?

A14)

S → aAbc

→ abAc

→ abBbcc

→ aBbbcc

→ aaAbbcc

→ aabAbcc

→ aabbAcc

→ aabbBbccc

→ aabBbbccc

→ aaBbbbccc

→ aaabbbccc

The language generated by this grammar is {an bn cn | n≥1}.