Unit - 4

Vector differential calculus

Q1) What is the cross product?

A1)

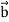The vector, or cross product of two vectors and is defined to be a vector such that

(i) Its magnitude is | || |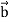sin , where is the angle between .

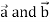(ii) Its direction is perpendicular to both vectors and

(iii) It forms with a right handed system.

Let 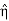be a unit vector perpendicular to both the vectors and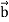

||

Q2) Define the vector product of three vectors.

A2)

Let 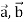and 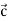be three vectors then their vector product is written as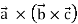

Let

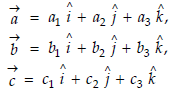
Q3) Prove that

A3)

Let

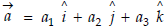
Now

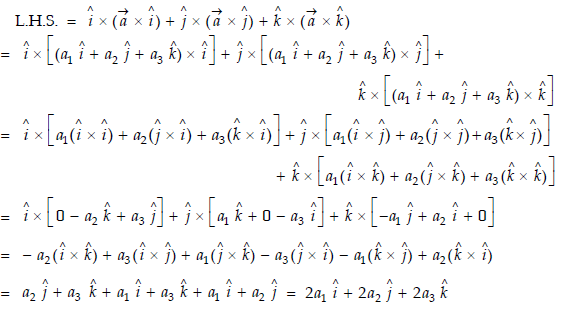
Q4) Show that

A4)

LHS

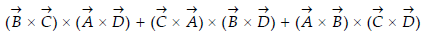
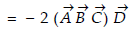
Hence proved

Q5) Define scalar point function and vector point function.

A5)

Scalar point function-

If for each point P of a region R, there corresponds a scalar denoted by f(P), in that case f is called scalar point function of the region R.

Vector point function-

If for each point P of a region R, then there corresponds a vector 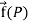then is called a vector point function for the region R.

Q6) Show that 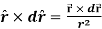 where

A6)

Here it is given-

=

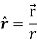
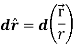
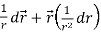
Therefore-

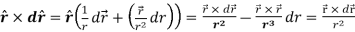Note-

Hence proved

Q7) What are the tangential and normal vectors?

A7)

Tangential and normal accelerations-

It is very important to understand that the magnitude of acceleration is not always the rate of change of |V|.

Suppose 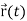be the vector-valued function which denotes the position of any object as a function of time.

Then

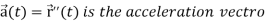
Then the tangential and normal component of acceleration are given as below-

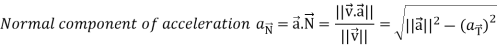
Q8) A object move in the path where t is the time in seconds and distance is measured in feets.

Then fi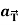nd and 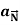as functions of t.

A8)

We know that-

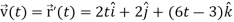
And

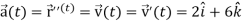
Now we will use-

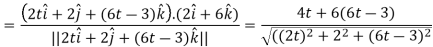
And now-

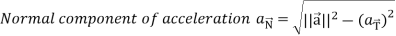
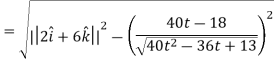
Q9) A particle moves along the curve 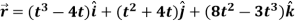, here ‘t’  is the time. Find its velocity and acceleration at t = 2.

A9)

Here we have-

Then, velocity

Velocity at t = 2,

=

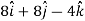
Acceleration =

Acceleration at t = 2,

Q10) If and 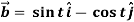then find-

1.

2.

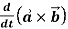
A10)

1. We know that-

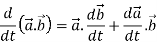
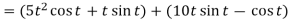
2.

Q11) If f and g are two scalar point functions, then show that

A11)

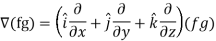
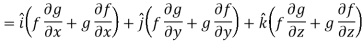
So that-

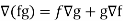
Hence proved.

Q12) If then find grad f at the point (1,-2,-1).

A12)

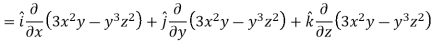
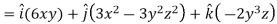
Now grad f at (1 , -2, -1) will be-       

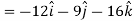
Q13) If 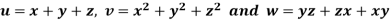then prove that grad u , grad v and grad w are coplanar.

A13)

Here-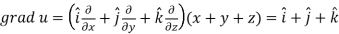                     

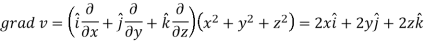
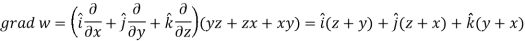
Now-

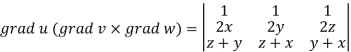
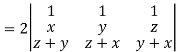
Apply

Which becomes zero.

So that we can say that grad u, grad v and grad w are coplanar vectors.

Q14) Show that-

1.

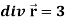
2.

A14)

We know that-

2. We know that-

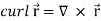
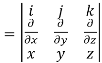
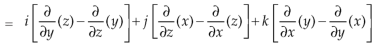
= 0

Q15) If 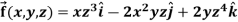then find the divergence and curl of .

A15)

We know that-

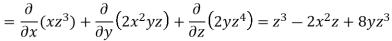
Now-

Q16) Find the curl of F(x,y,z) = 3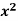i+2zj-xk

A16)

Curl F =

=

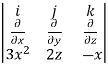
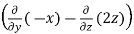= i -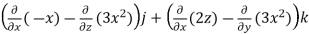

= (0-2)i-(-1-0)j+(0-0)k

= -2i+j

Q17) What is the curl of the vector field F= ( x +y +z ,x-y-z,)?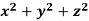

A17)

Curl F =

=

=

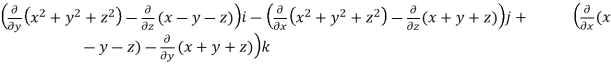
= (2y+1)i-(2x-1)j+(1-1)k

= (2y+1)i+(1-2x)j+0k

= (2y+1, 1-2x,0)

Q18) Find the directional derivative of 1/r in the direction 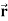where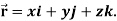

A18)

Here

Now,

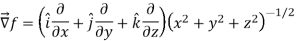
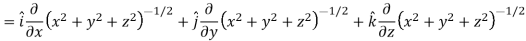
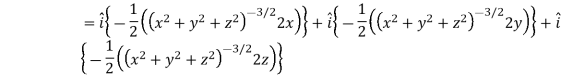
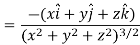
And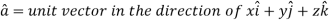

We know that-

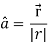
So that-

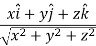
Now,

Directional derivative =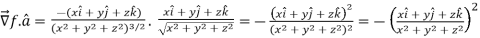

Q19) Find the directional derivatives of at the point P(1, 1, 1) in the direction of the line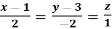

A19)

Here

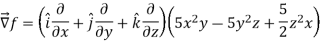
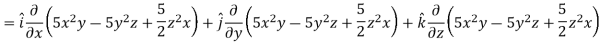
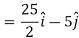
Direction ratio of the line are 2, -2, 1

Now directions cosines of the line are-

Which are

Directional derivative in the direction of the line-

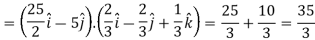
Q20) Prove that the vector field is irrotational and find its scalar potential.

A20)

As we know that if 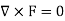then field is irrotational.

So that-

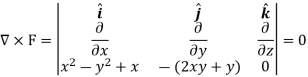
So that the field is irrotational and the vector F can be expressed as the gradient of a scalar potential,

That means-

Now-

   ………………… (1)

  ……………………. (2)

Integrating (1) with respect to x, keep ‘y’ as constant-

We get-

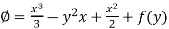      …………….. (3)

Integrating (1) with respect to y, keep ‘x’ as constant-

We get-

      …………….. (4)

Equating (3) and (4)-

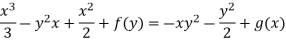
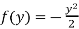and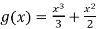

So that-