Unit - 4

Partial Differential Equations

Q1) What is Partial differential equations of first order first degree?

A1)

A partial differential equation (PDE) is an equation involving one or more partial derivatives of an (unknown) function, call it u, that depends on two or more variables, often time t and one or several variables in space. The order of the highest derivative is called the order of the PDE. Just as was the case for ODEs, second-order PDEs will be the most important ones in applications.

Just as for ordinary differential equations (ODEs) we say that a PDE is linear if it is of the first degree in the unknown function u and its partial derivatives. Otherwise, we call it nonlinear.

The standard methods of solving the differential equations of the following

Types:

1. Equations solvable by separation of the variables.
2. Homogeneous equations.
3. Linear equations of the first order.
4. Exact differential equations.

The differential equation of first order and first degree is namely:

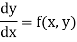
And

M(x, y)dx + N(x, y) dy = 0

Q2) Solve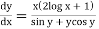

A2)

We have,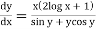

Separating the variables, we get

(sin y + y cos y) dy = {x (2 log x +1} dx

Integrating both the sides we get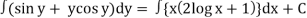

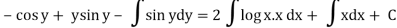
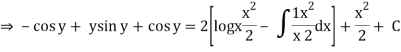
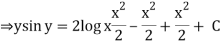
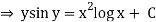
Q3) Solve the differential equation

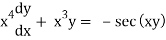
A3)

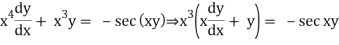
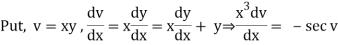
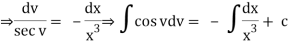
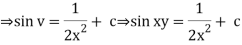
Q4) Write Linear Equations of the First Order

A4)

Linear Equations of the First Order

A linear partial differential equation of the first order, commonly known as Lagrange’s Linear equation is of the for4m

Pp + Qq = R              (1)

Where, P, Q and R are functions of x, y, z. This equation is called a quast linear equation. When P, Q and R are independent of z it is known as linear equation.

Such asn equation is obtained by eliminating an arbitrary function ϕ from  ϕ  (u, v) = 0 ....(2)

Where u,v are are some functions of x, y, z.

Differentiating (2) partially with respect to x and y

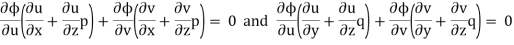
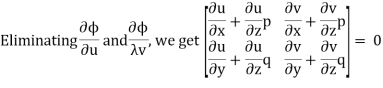
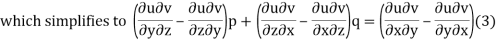
This is of the same form as (1)

Now suppose u = a and v=b, where a, b are constants, so that

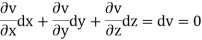
By cross multiplication we have,

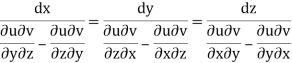
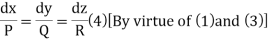
The solution of these equations are u = a and v = b

Therefore, ϕ(u, v) = 0 is the required solution of (1).

Thus, to solve the equation Pp + Qq =R.

(i) Form the subsidiary equations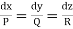                 

(ii) Solve these simultaneous equations

(iii) Write the complete solution as ϕ(u, v) = 0 or u = f(v)

Q5) Solve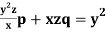

A5)

Rewriting the given equation as

The subsidiary equations are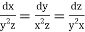                

The first two fractions give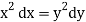

Integrating we get 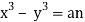(i)

Again, the first and third fraction give xdx = zdz

Integrating, we get

Hence from (i) and (ii), the complete solution is

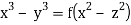
Q6) Solve

A6)

Here the subsidiary equations are

Using multipliers x, y and z we get each fraction =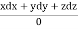

Xdx + ydy + zdz = 0 which on integration gives x2 + y2 + z2 = a    (i)

Again, using multipliers l, m and n we get each fraction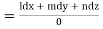

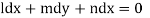which on integration gives lx +my +nz = b (ii)

Hence from (i) and (ii) the required solution is x2 + y2 + z2 = f(lx + my + nz)

Q7) Solve (x2 - y2 - z2)p + 2xyq = 2xz

A7)

Here the subsidiary equations are

From the last two fractions, we have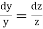

Which on integration gives log y = log z + log a or y/z=a (i)

Using multipliers x, y and z we have

Each fraction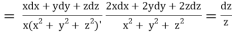 

Which on integration gives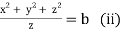

Hence from (i) and (ii) the required solution is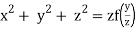

Q8) Using the method of separation of variables, solve

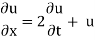
A8)

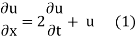
Let, u = X(x). T (t).                     (2)

Where X is a function of x only and T is a function of t only.

Putting the value of u in (1), we get

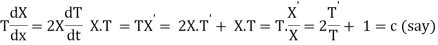
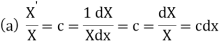
On integration log X = cx + log a = log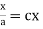

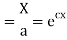
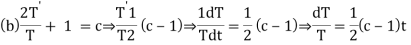
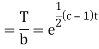
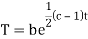
Putting the value of X and T in (2) we have

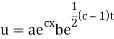
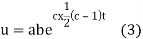
u(x, 0) = abecx

But,   u(x, 0) = 6e-3x

i.e.abecx = 6e-3x

= ab = 6 and c = - 3

Putting the value of a b and c in (3) we have

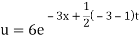
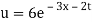
Which is the required solution.

Q9) Use the method of separation of variables to solve the equation

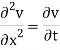
Given that v = 0 when t→∞  as well as v =0 at x = 0 and x = 1.

A9)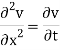
 

Let us assume that v = XT where X is a function of x only and T that of t only

Substituting these values in (1), we get

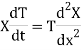
Let each side of (2) equal to a constant (-p2)

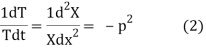
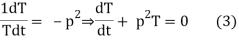
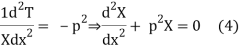
Solving (3) and (4) we have

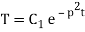
X = C2cospx + C3 sinpx      (5)

v = C1 (C2 cospx + C3 sin px)

Putting x = 0, v = 0 in (5) we get

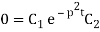
C2 = 0, since C1 ≠ 0

On putting the value of C2 in (5) we get

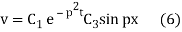
Again putting x = l, v= 0 in (6) we get

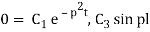
Since C3 cannot be zero.

Sinpl = 0 = sinnπ

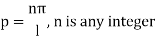
Inputting the value of p in (6) it becomes

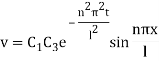
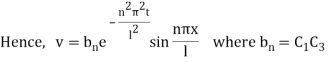
This equation satisfies the given condition for all integral values of n. Hence taking n = 1, 2, 3,… the most general solution is

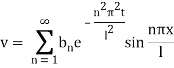
Q10) Using the method of separation of variables, solv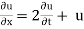e Where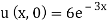

A10)

Assume the given solution u(x, t) = X(x)T(t)

Substituting in the given equation, we have

XT = 2XT' + XT or (X' - X)T = wXT'

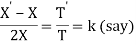
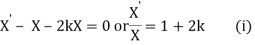
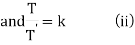
Solving (i) log X = (1+2k)x + logc or X = ce(1+2k)x

From (ii) log T = kt + log c' or T = c'ekt

Thus u(x, t) = XT = cc'e(1+2k)xekt      (iii)

Now,  6e-3x = u(x, 0) = cc'e(1+2k)x

Cc' = 6  and  1+2k = -3 or k = -2

Substituting these values in (iii) we get

u = 6e-3x e-2t i.e. u = 6e-(3x+2t)

Which is the required solution