Unit - 3
Strain energy method
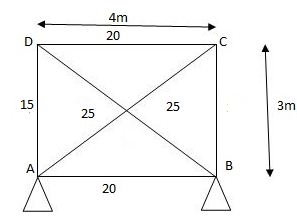
Q1) EI = 17250 Kn.m2 find strain energy?
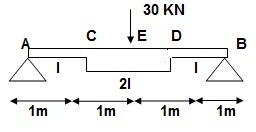
A1)
∑MA = 0
30 x 2 – RB x 4 = 0
RB = 15
VA = VB = 15 KN
BMC = BMD = 15(1) = 15 KN.M
BMC = 15(2) = 30 KN.M

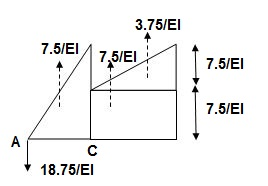
‘M/EI’ Dia.
C.B
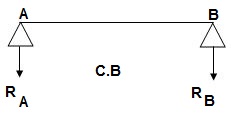
A1 = 1 / 2 x 1 x 15/EI = 7.5/EI
A2 = 2 x 7.5/EI = 15/EI
A3 = 1 /2 x 2 x 7.5/EI = 7.5/EI
A4 = 1 / 2 x 15/EI x 1 = 7.5/EI
Analysis of conjugate beam:
∑MA = -RB(4) + 1/EI{7.5(2/3 x 1) + 15(2) + 7.5(2) + 7.5(3 + 1/31)} = 0
= - RB x 4 + 1/EI[ 5 + 30 + 15 + 25 ] = 0
RB x 4 = 75/17250
RB = 18.75/EI
∑fy = 0
-RA + RB + A1 + A2 + A3 + A4 = 0
RA = 18.75/EI
RA = RB = ½{A1 + A2 + A3 + A4} = 18.75/EI
Slope & Deflection:
(ϴA)R.B = (SFA)C.B = (-)18.75/EI
= 18.75/EI  = 1.086 x 10-3rad
= 1.086 x 10-3rad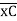
(ϴB)R.B = (SFB)C.B = 18.75/EI = 1.086 x 10-3 rad
= 1.086 x 10-3 rad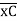
(ΔE)R.B = (BME)CB
(BME)CB= 1/ EI { -18.75 + 7.5(1 + 1/3 x 1) + 7.5(0.5) + 3.75 (1/3 x 1)}
=1/ EI {-22.5}
ΔE = 22.5/EI  = 1.304 mm
= 1.304 mm 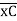
Q2) Explain unit load method for statically determinate beams, frames and trusses.
A2)
The unit load method helps us in finding the displacement D, at the coordinate in a structure, whose deformations are either known or can be derived. In just-rigid structures, the internal displacement field is generally known in problems of indirect loading, such as due to environmental effects and constructional errors ("lack of fit' in trusses), and it is desired to find a joint displacement that is compatible with the deformation. More commonly, we encounter problems involving direct actions, where the deformations are not given, but can be derived from the internal force response. For example, we can calculate bar elongations in truss members, if we know the axial forces in the bars. Similarly, from the bending moment distribution in flexural members, we can derive the curvatures.
Assuming linear elastic behavior (we have the following well known relationships:
(a) Between bar elongation e, and axial force N, in a truss member (having an axial rigidity EA and length L)
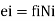
Where, the subscript i refer to the i bar (truss element), whose axial flexibility f, is given by
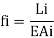
(b) Between curvature 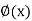 - (having flexural rigidity(El) de and bending moment M(x) in a flexural member
- (having flexural rigidity(El) de and bending moment M(x) in a flexural member
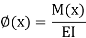
Q3) Explain application of trusses in detail.
A3)
Consider a truss with some (real) displacement field, which may be caused by direct or indirect loading. The elongation e in all the bars are known and it is desired to find some joint displacement D, at the coordinate. If the cause is loading by direct actions, the bar forces N, can be analyzed and the corresponding bar elongations e, are easily obtainable by applying Eq. This is depicted in Fig. If the cause is due to lack of fit or temperature change, and the truss is just-rigid, the values of e, are known.
Now, consider the same truss and apply a virtual unit load, F= 1 at the coordinate as shown in Fig. Analyze the truss and arrive at all the virtual bar forces n. The force in the bar may be denoted as nij, i.e, caused by unit load applied at j.
Combining the real and virtual force fields shown in Fig.we can write the expressions for virtual work:
External work

Internal work
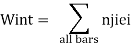
Applying the Principle of virtual work,
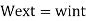

Note that D, has the same unit (dimension) as e, (usually in mm). Is dimensionally homogeneous because the bar force n (caused by a unit load) is dimensionless, having units of kN/kN.
Q4) Give application to Beams and Frames
A4)
Consider a beam with some (real) displacement field, which may be caused by direct or indirect loading. The variation of curvature p(x) along the length of the beam is known and it is desired to find a deflection or a rotation DJ at the coordinate. If the cause is loading by direct actions, the bending moments M(x) can be analyzed, and the corresponding curvatures P(x) are easily obtainable by applying Eq. This is depicted in Fig. If the cause is due to indirect loading (such as due to differential shrinkage in a reinforced concrete beam), the distribution of curvatures should be known
Now, consider the same beam and apply a virtual unit load F-1 as shown in Fig.. Analyze the beam and arrive at the bending moment’s m(x).
Combining the real and virtual force fields shown in Fig. We can write the expressions for virtual work:

External work
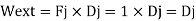
Internal work
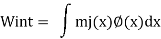
Applying the principle of virtual work

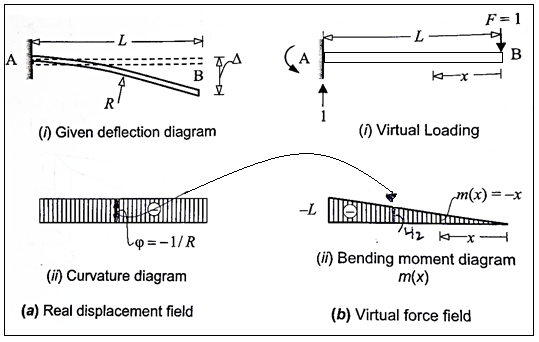
Q5) Considering a cantilever beam length L bent to a segment of a circle of radius R. Find the deflection at the free end.
A5)
The curvature length as given in beam in constant with 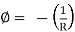 as shown in fig
as shown in fig
Applying the principle of virtual work
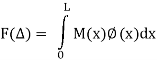
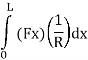
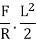
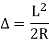
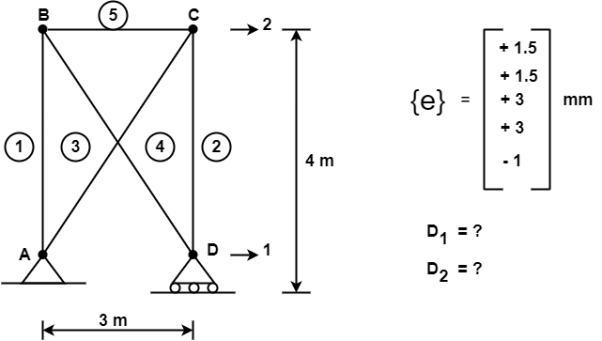
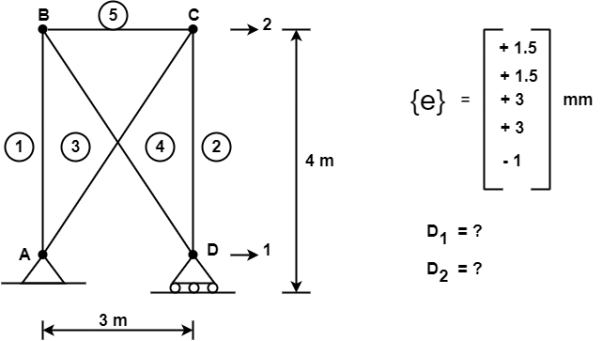
Q6) Consider the pin jointed truss in fig. With bars numbered as indicated. Due to certain environmental change bar 1 and 2 increase in length by 1.5 mm bars 3 and 4 increases in length by 3 mm and bar 5 reduce in length by 1 mm find the horizontal movement of ith the roller support at D and the joint C
A6)
The bar elongations gives form part of a real displacement filed with
{e} = { +1.5,+1.5.+3,+3,-1}^T mm
The required horizontal joint displacement at D and C are identified as Di and Dj resp. Using the co ordinate system in shown in fig.
Applying unit load method
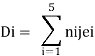

Where ni1 and ni2 are the force the ith bar due to F1 = 1 and F2 = 1
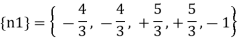
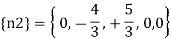
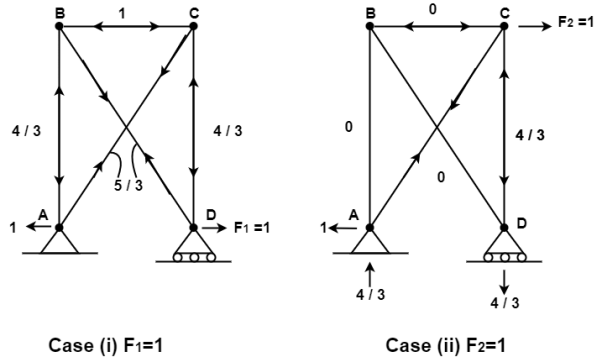
Therefore the horizontal movement at the roller support is given by
Case 1 Horizontal deflection D1 of the support D
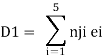
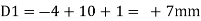
Case 2 Horizontal deflection D2 of a joint C

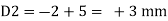
Q7) Explain determination of deflection of trusses.
A7)
1) Determine deflection of trust joint
1) Determine P force by given load system using joint method.
2) Remove given loud system & apply unit load to joint where the deflection desired find K force.
3) Determine PKl/ AI of each member
4) Deflection of the joint = ∑ PKl / AE
2) Analysis of indeterminate plane truss
1) Find the degree of indeterminacy
2) Select redundant member
3) Remove redundant member and find the force P in the members of the truss.
4) Remove the given loud system
a) Apply a unit load paid (either textile/ amp) in place of redundant member.
b) Find k force.
5) PKl / AE & K2L / AE
6) Correction factor = x = ∑ PKl / AE P = (P + KX) / ∑ K2L/ AE
Lock of fit of members in trust
Lock of fit is defined as little or little shorter length of any in trust.
Correction factor due to lack of
x = x (- ∑ PKl / AE) / (∑ K2L/ AE)
Where
x = shortening or excess of members
+ve = if member is short in length
-ve = if member is short in long
Find force = f = P + Kx
Formula for truss
1) Find detection -
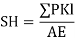

2) Analyze indeterminate
i) F = P + KX x = (∑PKl/AE) / (∑K2l/AE)
Ii) for lock of fit =
Sign convention -ve for short member
+ve for long member
Iii) for Temp effect P = QK
Q = (xlt) / ∑ K2l/AE
Iv) for yield support
F = P + QK
DQ = DQL + FQ
DQ = Sink
DQL = ∑ PKl / AE
F = ∑ K2l / AE
2)
AD in short by
E = 200 Gpa
FAB = 28.04 KN FOC = 21.08
FOD = 28.04 KN FDA = 21.28
FDB = 35./20 KN FAC = 30.
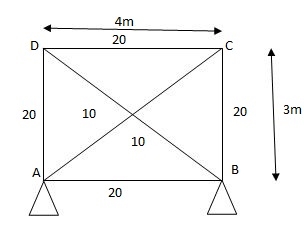
Q8) Analyze the truss supported as shown in fig. If member AD is subjected to temp drop of 300C Taken E= 200Gpa&coeff. Thermal expansion = 1.1 x 10-5/oc C/S area of each member in cm2 is indicated in brackets.
A8)
Given:
AD is subjected to Temp drop 300C.
AD is redundant member consist unit load due to drop -ve sign
Joint A
Efy = 0
KAC5in 36.86 + 1 = 0
KAC = - 1.67 KN
Efx = 0
KAB + KAC COS 36.86 = 0
KAB = 1.34 KN
Joint D
Efy = 0
KDBsin 36.86 – 1 = 0
KDB = - 1.67 KDC = 1.33
Sr.No. | Member | Length | Area | K | …. | Q | …. |
AB |
| 4000 | 2000 | 1.33 | 3.56 |
| 11.84 |
BC |
| 3000 | 1000 | 1 | 2 |
| 8.9 |
CD |
| 4000 | 2000 | 1.33 | 3.56 | 8.9 | 11.84 |
DA |
| 3000 | 1000 | 1 | 5.56 |
| 8.90 |
DB |
| 5000 | 2000 | - 1.67 | 5.56 |
| -14.86 |
AC |
| 5000 | 2000 | - 1.67 | 2 |
| -14.86 |
P = QK
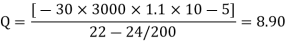
P = 8.90 x K
c/s area 10m2, rise of kmp of member BD by 300c
= 12 x 10-6 /oc E= 200Gpa.
FBC = 17.77KN, FCD = 13.33 KN FAD = 12.77KN
FAC = 22.22 KN FBD = 22.22 KN FDE = FCE = 0
Q9) Analyze the truss supported as shown in fig., if support B sink by 3mm & c/s area of each member 400mm2.
A9)
Joint A
Efx = 0
PAB + PAE COS45 – 20 = 0
PAB + PAECOS45 – 20 (1)
Efy = 0
PAESin45 – PAF + ……. = 0
PAE = 38.89 KN
PAB + - 38.89 ……… = 20
PAB = 47.49 …
Joint B
Efx = 0
- PBA + PBC = 0
PBC = 47.49 KN
PEB = 0KN
Find k force

By observation
Joint A
Efx = 0
KAB + KAE COS45 = 0
KAE Sin45 + 0.5 = 0
KAE = - 0.707
KAB = - 0.49
Sr.No. | Member | Length | P | K | PK8 | P2B | F= P+ |
1. | AB | 3000 | 47.5 | -0.5 | -23.75 | + 0.25 | 76.1 |
2. | BC | 3000 | 47.5 | -0.5 | -23.75 | + 0.25 |
|
3. | CD | 3000 | 0 | 0 | 0 | 0 |
|
4. | DE | 3000 | -20 | 0 | 0 | 0 |
|
5. | EF | 3000 | -20 | 0 | 0 | 0 |
|
6. | AE | 3000 | -38.89 | -0.707 | 24.5 | 0.49 |
|
7. | EC | 3000 | -38.89 | -0.707 | 24.5 | 0.49 |
|
8. | BE | 3000 | 0 | 1 | 0 | 0 |
|
9. | AF | 4242.6 | 0 | 0 | 0 | 0 |
|
|
|
|
| E | 4500 | 1.49 X 3000 = 4440 | |
DQ = DQL + FQ
DQ1 = EPKl / AC = 0.053
F= EK2l / AE = 0.0528
DQ = 3mm
Indeterminate trusses with lack of f/f
DQ = DQF + FQ DQ = O
Q = - DQF/ K2L /AE F =K2L
DQF is +ve if the member is long
DQF is -ve if the member is short
Q10) Analyze the truss supported as show in fig. If the member AB is short by 5mm Take E= 200 Gpa c/s area of each member in is indicated in brackets.
A10)
AB = 5mm short consider -ve sign
E = 200 Gpa
1cm = 10mm
1m = 103mm
Sr.No. | Member | Length | Area | K | K2l |
1. | AD | 2795 | 1500 | 2.23 | 9.35 |
2. | BD | 2795 | 1500 | 2.23 | 9.35 |
3. | AC | 3535 | 3000 | -1.41 | -2.34 |
4. | BC | 3535 | 3000 | -1.41 | -2.34 |
5. | CD | 1250 | 1000 | 2 | 5.00 |
6. | AB | 5000 | 1500 | 1 | 3. |
|
|
|
| EK | 31.71 |
Q = DQF/ K2l /AE = - 5000 Q = 91.54
P = QK
Joint A
Ek = 0
KADCOS 26.26 + KAC COS 45-1
KADsin26.26 + KAC sin45 = 0
KAD = 2.23
KAC = - 1.41
Q11) Explain castiglione’s1sttheorem.
A11)
It states that displacement at a point of application of load in the direction of load is equal to partial derivative of strain energy of structure with respect to load.
1]. ӘU/ӘQi = Δj
U = strain energy
Qj = Force in the direction j
Δj = Displacement in the direction j
2]. Strain energy: UAxial force = ∫L0P2dx/2EA
UB.M = ∫L0M2dx/2EI
UTorsion = ∫L0T2dx/2GJ
Deflection = translation
3]. Procedure of displacement analysis by Castiglinos theorem:
Step 1:
Apply imaginary load ‘Q’ at section where displacement is required.
Note:
1. For horizontal translation apply ‘Q’ in horizontal direction For vertical translation apply force Q in vertical direction
2. For finding ‘slope’(rotation) apply couple Q.
Step 2: Find support reactions and draw member F.B.D’s
Step 3: Prepare table:
Zone origin limits EI M ӘM/ӘQ
Step 4: Find displacement using Δj = ∫L0M/EI{ӘM/ӘQj}dx
Find ΔB:
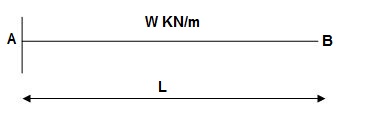
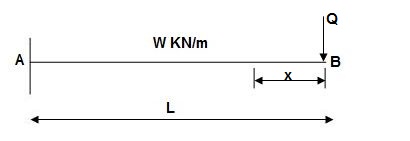
Zone Origin Limits EI M ӘM/ӘQ
BA B 0 to L EI –Q(x) – W(x2/2)-x
ΔB = ∫L0 M/EI(ӘM/ӘQ)dx = ∫L0{-W(x2/2)}(-x)dx
= W/2EI{x4/4}L0
Q12) Find Vertical deflection at ‘c’
EI = constant

A12)
M Diagram
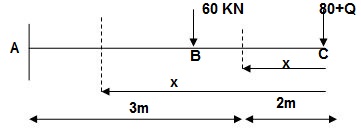
From above Fig:
Table
Zone Origin limits EI M ӘM/ӘQj
CB C 0-2 EI -(80 + Q)x - x
BA C 2-5 EI -(80 + Q)x - x-60(x-2)
ΔC = ∫20-(80)x/EI {-x}dx + ∫52{80x – 60(x-2) (-x) dx/EI}
= ∫2080x2/EIdx + ∫52{80x2 – 60x2 + 2x}dx/EI
= 1/EI{213.33 + 4200}
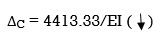
Q13) Find vertical deflection at point C

A13)
M Diagram
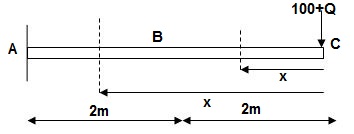
Zone Origin Limit EI M ӘM/ӘQ
CB C 0 – 2 EI - (100 + Q)x -x
BA C 2 – 4 EI -(100 + Q)x -x
ΔC = ∫20 – 100x/EI(-x)dx + ∫42 -100x/EI(-x)dx
= ∫20100x2/EIdx + ∫42100x2/2EIdx
= 266.66 + 1866.6/2 = 266.66 + 933.33
For cantilever always write load from free end. For simply write load from supports.
ΔC = 1200/EI
Q14) Find slope at deflection ‘A’, deflection at ‘C’.
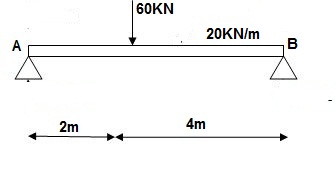
A14)
M Diagram
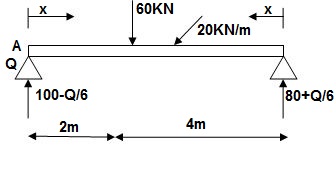
Reactions in M dia.
∑MA = VB(6) – 20 x 6 x 3 – 60(2) – Q = 0
VB = 80 + Q/6
∑Fy = VA + VB – 60 – 20 x 6 = 0
VA = 100 – Q/6
Zone Origin limits EI M ӘM/ӘQ
AC A 0 – 2 EI (100-Q/6)(x) 1 – x/6+ Q – 20(x2/2)
BC B 0 – 4 EI (80+Q/6)(x)-20x2/2 x/6
ϴA = ∫20{100(x) – 10x2}{1-x/6}dx/dEI + ∫40{80x – 10x2}x/6dx/EI
= 1/EI{135.55 + 177.78}
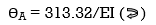
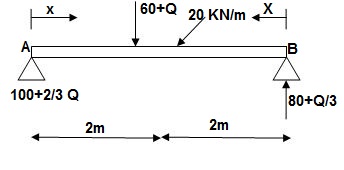
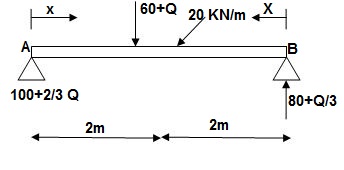
∑MA = VB(6) – 20(6)(3) – (60 + Q)2 = 0
VB = 80 + Q/3
∑Fy = VA + VB – (60 + Q) – 20(6) = 0
VA = -80 – Q/3 + 60 + Q + 120 = 0
VA = 100 + 2/3Q
Q15) Find a deflection at a point C
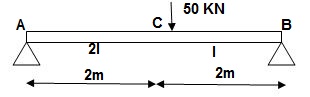
A15)
M Diagram
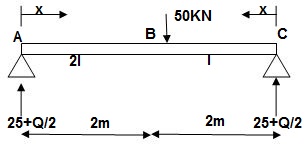
Zone Origin Limit EI MӘM/ӘQ
AC A 0 – 2 EI (25 + Q/2)x x/2
BC B 0 – 2 EI (25 + Q/2)x x/2
ΔC = ∫20(25x)x/2dx/EI + ∫2025x(x/2)dx/2EI
= 33.33 + 16.66/EI

Unit - 3
Unit - 3
Strain energy method
Q1) EI = 17250 Kn.m2 find strain energy?
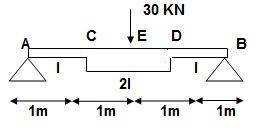
A1)
∑MA = 0
30 x 2 – RB x 4 = 0
RB = 15
VA = VB = 15 KN
BMC = BMD = 15(1) = 15 KN.M
BMC = 15(2) = 30 KN.M
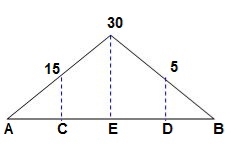
‘M/EI’ Dia.
C.B
A1 = 1 / 2 x 1 x 15/EI = 7.5/EI
A2 = 2 x 7.5/EI = 15/EI
A3 = 1 /2 x 2 x 7.5/EI = 7.5/EI
A4 = 1 / 2 x 15/EI x 1 = 7.5/EI
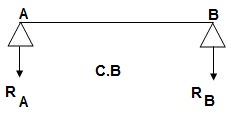
Analysis of conjugate beam:
∑MA = -RB(4) + 1/EI{7.5(2/3 x 1) + 15(2) + 7.5(2) + 7.5(3 + 1/31)} = 0
= - RB x 4 + 1/EI[ 5 + 30 + 15 + 25 ] = 0
RB x 4 = 75/17250
RB = 18.75/EI
∑fy = 0
-RA + RB + A1 + A2 + A3 + A4 = 0
RA = 18.75/EI
RA = RB = ½{A1 + A2 + A3 + A4} = 18.75/EI
Slope & Deflection:
(ϴA)R.B = (SFA)C.B = (-)18.75/EI
= 18.75/EI  = 1.086 x 10-3rad
= 1.086 x 10-3rad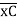
(ϴB)R.B = (SFB)C.B = 18.75/EI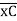 = 1.086 x 10-3 rad
= 1.086 x 10-3 rad
(ΔE)R.B = (BME)CB
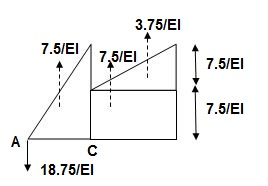
(BME)CB= 1/ EI { -18.75 + 7.5(1 + 1/3 x 1) + 7.5(0.5) + 3.75 (1/3 x 1)}
=1/ EI {-22.5}
ΔE = 22.5/EI 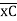 = 1.304 mm
= 1.304 mm 
Q2) Explain unit load method for statically determinate beams, frames and trusses.
A2)
The unit load method helps us in finding the displacement D, at the coordinate in a structure, whose deformations are either known or can be derived. In just-rigid structures, the internal displacement field is generally known in problems of indirect loading, such as due to environmental effects and constructional errors ("lack of fit' in trusses), and it is desired to find a joint displacement that is compatible with the deformation. More commonly, we encounter problems involving direct actions, where the deformations are not given, but can be derived from the internal force response. For example, we can calculate bar elongations in truss members, if we know the axial forces in the bars. Similarly, from the bending moment distribution in flexural members, we can derive the curvatures.
Assuming linear elastic behavior (we have the following well known relationships:
(a) Between bar elongation e, and axial force N, in a truss member (having an axial rigidity EA and length L)
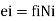
Where, the subscript i refer to the i bar (truss element), whose axial flexibility f, is given by
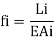
(b) Between curvature 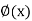 - (having flexural rigidity(El) de and bending moment M(x) in a flexural member
- (having flexural rigidity(El) de and bending moment M(x) in a flexural member

Q3) Explain application of trusses in detail.
A3)
Consider a truss with some (real) displacement field, which may be caused by direct or indirect loading. The elongation e in all the bars are known and it is desired to find some joint displacement D, at the coordinate. If the cause is loading by direct actions, the bar forces N, can be analyzed and the corresponding bar elongations e, are easily obtainable by applying Eq. This is depicted in Fig. If the cause is due to lack of fit or temperature change, and the truss is just-rigid, the values of e, are known.

Now, consider the same truss and apply a virtual unit load, F= 1 at the coordinate as shown in Fig. Analyze the truss and arrive at all the virtual bar forces n. The force in the bar may be denoted as nij, i.e, caused by unit load applied at j.
Combining the real and virtual force fields shown in Fig.we can write the expressions for virtual work:
External work
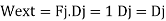
Internal work

Applying the Principle of virtual work,
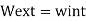

Note that D, has the same unit (dimension) as e, (usually in mm). Is dimensionally homogeneous because the bar force n (caused by a unit load) is dimensionless, having units of kN/kN.
Q4) Give application to Beams and Frames
A4)
Consider a beam with some (real) displacement field, which may be caused by direct or indirect loading. The variation of curvature p(x) along the length of the beam is known and it is desired to find a deflection or a rotation DJ at the coordinate. If the cause is loading by direct actions, the bending moments M(x) can be analyzed, and the corresponding curvatures P(x) are easily obtainable by applying Eq. This is depicted in Fig. If the cause is due to indirect loading (such as due to differential shrinkage in a reinforced concrete beam), the distribution of curvatures should be known
Now, consider the same beam and apply a virtual unit load F-1 as shown in Fig.. Analyze the beam and arrive at the bending moment’s m(x).
Combining the real and virtual force fields shown in Fig. We can write the expressions for virtual work:

External work

Internal work
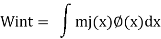
Applying the principle of virtual work

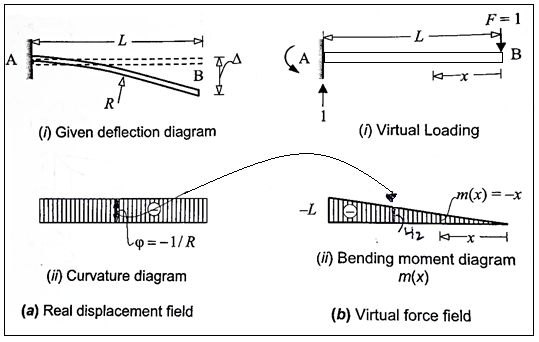
Q5) Considering a cantilever beam length L bent to a segment of a circle of radius R. Find the deflection at the free end.
A5)
The curvature length as given in beam in constant with 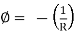 as shown in fig
as shown in fig
Applying the principle of virtual work
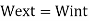


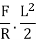

Q6) Consider the pin jointed truss in fig. With bars numbered as indicated. Due to certain environmental change bar 1 and 2 increase in length by 1.5 mm bars 3 and 4 increases in length by 3 mm and bar 5 reduce in length by 1 mm find the horizontal movement of ith the roller support at D and the joint C
A6)
The bar elongations gives form part of a real displacement filed with
{e} = { +1.5,+1.5.+3,+3,-1}^T mm
The required horizontal joint displacement at D and C are identified as Di and Dj resp. Using the co ordinate system in shown in fig.
Applying unit load method
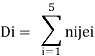
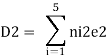
Where ni1 and ni2 are the force the ith bar due to F1 = 1 and F2 = 1

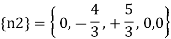
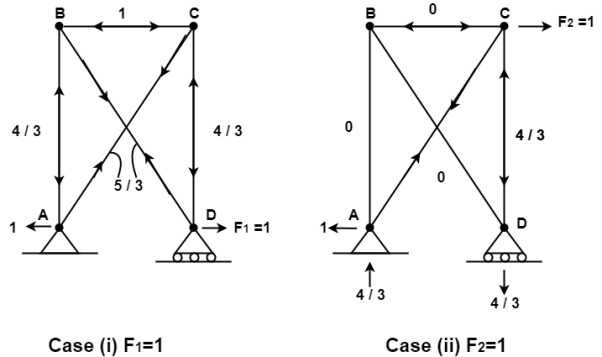
Therefore the horizontal movement at the roller support is given by
Case 1 Horizontal deflection D1 of the support D
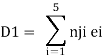
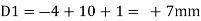
Case 2 Horizontal deflection D2 of a joint C


Q7) Explain determination of deflection of trusses.
A7)
1) Determine deflection of trust joint
1) Determine P force by given load system using joint method.
2) Remove given loud system & apply unit load to joint where the deflection desired find K force.
3) Determine PKl/ AI of each member
4) Deflection of the joint = ∑ PKl / AE
2) Analysis of indeterminate plane truss
1) Find the degree of indeterminacy
2) Select redundant member
3) Remove redundant member and find the force P in the members of the truss.
4) Remove the given loud system
a) Apply a unit load paid (either textile/ amp) in place of redundant member.
b) Find k force.
5) PKl / AE & K2L / AE
6) Correction factor = x = ∑ PKl / AE P = (P + KX) / ∑ K2L/ AE
Lock of fit of members in trust
Lock of fit is defined as little or little shorter length of any in trust.
Correction factor due to lack of
x = x (- ∑ PKl / AE) / (∑ K2L/ AE)
Where
x = shortening or excess of members
+ve = if member is short in length
-ve = if member is short in long
Find force = f = P + Kx
Formula for truss
1) Find detection -
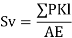
2) Analyze indeterminate
i) F = P + KX x = (∑PKl/AE) / (∑K2l/AE)
Ii) for lock of fit =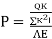
Sign convention -ve for short member
+ve for long member
Iii) for Temp effect P = QK
Q = (xlt) / ∑ K2l/AE
Iv) for yield support
F = P + QK
DQ = DQL + FQ
DQ = Sink
DQL = ∑ PKl / AE
F = ∑ K2l / AE
2)

AD in short by
E = 200 Gpa
FAB = 28.04 KN FOC = 21.08
FOD = 28.04 KN FDA = 21.28
FDB = 35./20 KN FAC = 30.
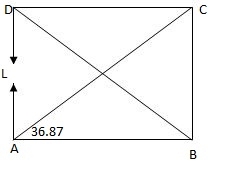
Q8) Analyze the truss supported as shown in fig. If member AD is subjected to temp drop of 300C Taken E= 200Gpa&coeff. Thermal expansion = 1.1 x 10-5/oc C/S area of each member in cm2 is indicated in brackets.
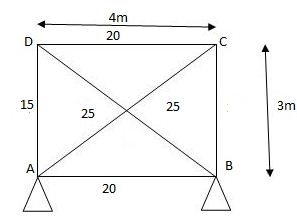
A8)
Given:
AD is subjected to Temp drop 300C.
AD is redundant member consist unit load due to drop -ve sign

Joint A
Efy = 0
KAC5in 36.86 + 1 = 0
KAC = - 1.67 KN
Efx = 0
KAB + KAC COS 36.86 = 0
KAB = 1.34 KN
Joint D
Efy = 0
KDBsin 36.86 – 1 = 0
KDB = - 1.67 KDC = 1.33
Sr.No. | Member | Length | Area | K | …. | Q | …. |
AB |
| 4000 | 2000 | 1.33 | 3.56 |
| 11.84 |
BC |
| 3000 | 1000 | 1 | 2 |
| 8.9 |
CD |
| 4000 | 2000 | 1.33 | 3.56 | 8.9 | 11.84 |
DA |
| 3000 | 1000 | 1 | 5.56 |
| 8.90 |
DB |
| 5000 | 2000 | - 1.67 | 5.56 |
| -14.86 |
AC |
| 5000 | 2000 | - 1.67 | 2 |
| -14.86 |
P = QK
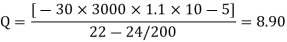
P = 8.90 x K
c/s area 10m2, rise of kmp of member BD by 300c
= 12 x 10-6 /oc E= 200Gpa.
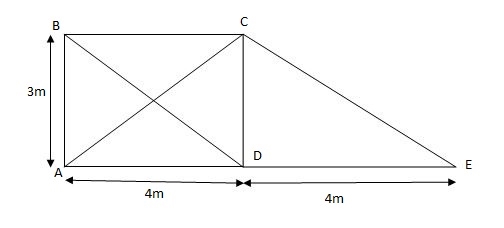
FBC = 17.77KN, FCD = 13.33 KN FAD = 12.77KN
FAC = 22.22 KN FBD = 22.22 KN FDE = FCE = 0
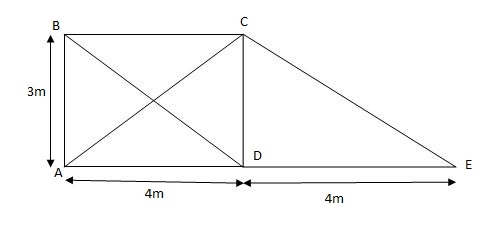
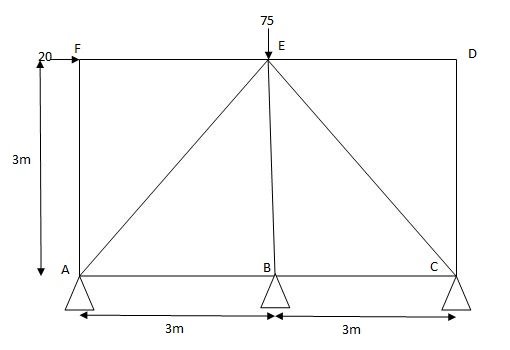
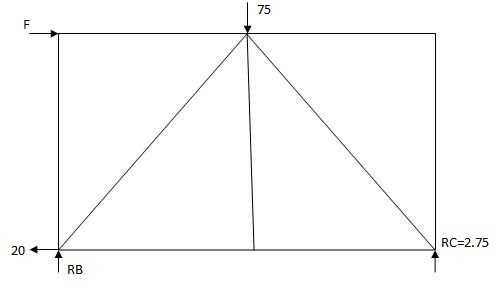
Q9) Analyze the truss supported as shown in fig., if support B sink by 3mm & c/s area of each member 400mm2.
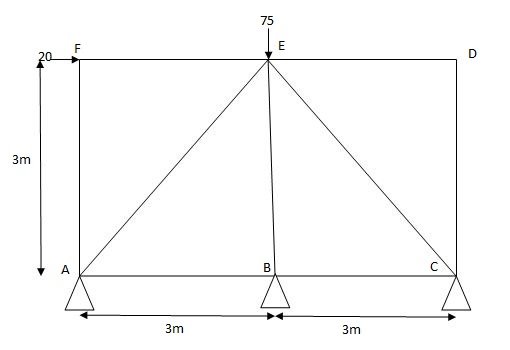
A9)
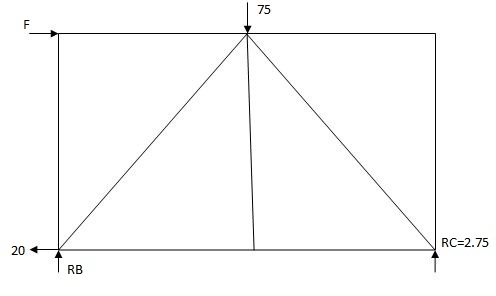
Joint A
Efx = 0
PAB + PAE COS45 – 20 = 0
PAB + PAECOS45 – 20 (1)
Efy = 0
PAESin45 – PAF + ……. = 0
PAE = 38.89 KN
PAB + - 38.89 ……… = 20
PAB = 47.49 …
Joint B
Efx = 0
- PBA + PBC = 0
PBC = 47.49 KN
PEB = 0KN
Find k force

By observation
Joint A
Efx = 0
KAB + KAE COS45 = 0
KAE Sin45 + 0.5 = 0
KAE = - 0.707
KAB = - 0.49
Sr.No. | Member | Length | P | K | PK8 | P2B | F= P+ |
1. | AB | 3000 | 47.5 | -0.5 | -23.75 | + 0.25 | 76.1 |
2. | BC | 3000 | 47.5 | -0.5 | -23.75 | + 0.25 |
|
3. | CD | 3000 | 0 | 0 | 0 | 0 |
|
4. | DE | 3000 | -20 | 0 | 0 | 0 |
|
5. | EF | 3000 | -20 | 0 | 0 | 0 |
|
6. | AE | 3000 | -38.89 | -0.707 | 24.5 | 0.49 |
|
7. | EC | 3000 | -38.89 | -0.707 | 24.5 | 0.49 |
|
8. | BE | 3000 | 0 | 1 | 0 | 0 |
|
9. | AF | 4242.6 | 0 | 0 | 0 | 0 |
|
|
|
|
| E | 4500 | 1.49 X 3000 = 4440 | |
DQ = DQL + FQ
DQ1 = EPKl / AC = 0.053
F= EK2l / AE = 0.0528
DQ = 3mm
Indeterminate trusses with lack of f/f
DQ = DQF + FQ DQ = O
Q = - DQF/ K2L /AE F =K2L
DQF is +ve if the member is long
DQF is -ve if the member is short
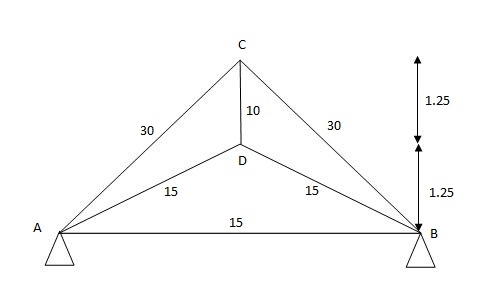
Q10) Analyze the truss supported as show in fig. If the member AB is short by 5mm Take E= 200 Gpa c/s area of each member in is indicated in brackets.

A10)
AB = 5mm short consider -ve sign
E = 200 Gpa
1cm = 10mm
1m = 103mm
Sr.No. | Member | Length | Area | K | K2l |
1. | AD | 2795 | 1500 | 2.23 | 9.35 |
2. | BD | 2795 | 1500 | 2.23 | 9.35 |
3. | AC | 3535 | 3000 | -1.41 | -2.34 |
4. | BC | 3535 | 3000 | -1.41 | -2.34 |
5. | CD | 1250 | 1000 | 2 | 5.00 |
6. | AB | 5000 | 1500 | 1 | 3. |
|
|
|
| EK | 31.71 |
Q = DQF/ K2l /AE = - 5000 Q = 91.54
P = QK
Joint A
Ek = 0
KADCOS 26.26 + KAC COS 45-1
KADsin26.26 + KAC sin45 = 0
KAD = 2.23
KAC = - 1.41
Q11) Explain castiglione’s1sttheorem.
A11)
It states that displacement at a point of application of load in the direction of load is equal to partial derivative of strain energy of structure with respect to load.
1]. ӘU/ӘQi = Δj
U = strain energy
Qj = Force in the direction j
Δj = Displacement in the direction j
2]. Strain energy: UAxial force = ∫L0P2dx/2EA
UB.M = ∫L0M2dx/2EI
UTorsion = ∫L0T2dx/2GJ
Deflection = translation
3]. Procedure of displacement analysis by Castiglinos theorem:
Step 1:
Apply imaginary load ‘Q’ at section where displacement is required.
Note:
1. For horizontal translation apply ‘Q’ in horizontal direction For vertical translation apply force Q in vertical direction
2. For finding ‘slope’(rotation) apply couple Q.
Step 2: Find support reactions and draw member F.B.D’s
Step 3: Prepare table:
Zone origin limits EI M ӘM/ӘQ
Step 4: Find displacement using Δj = ∫L0M/EI{ӘM/ӘQj}dx
Find ΔB:
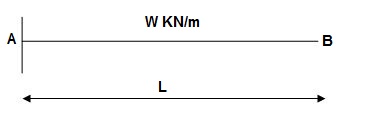
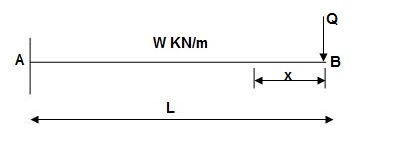
Zone Origin Limits EI M ӘM/ӘQ
BA B 0 to L EI –Q(x) – W(x2/2)-x
ΔB = ∫L0 M/EI(ӘM/ӘQ)dx = ∫L0{-W(x2/2)}(-x)dx
= W/2EI{x4/4}L0

Q12) Find Vertical deflection at ‘c’
EI = constant
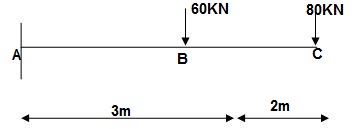
A12)
M Diagram
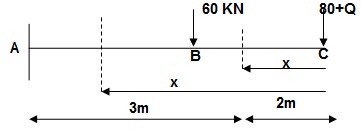
From above Fig:
Table
Zone Origin limits EI M ӘM/ӘQj
CB C 0-2 EI -(80 + Q)x - x
BA C 2-5 EI -(80 + Q)x - x-60(x-2)
ΔC = ∫20-(80)x/EI {-x}dx + ∫52{80x – 60(x-2) (-x) dx/EI}
= ∫2080x2/EIdx + ∫52{80x2 – 60x2 + 2x}dx/EI
= 1/EI{213.33 + 4200}
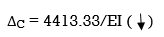
Q13) Find vertical deflection at point C
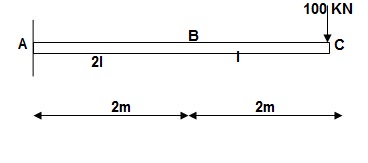
A13)
M Diagram
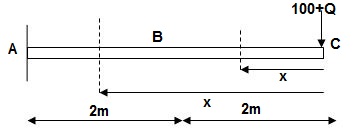
Zone Origin Limit EI M ӘM/ӘQ
CB C 0 – 2 EI - (100 + Q)x -x
BA C 2 – 4 EI -(100 + Q)x -x
ΔC = ∫20 – 100x/EI(-x)dx + ∫42 -100x/EI(-x)dx
= ∫20100x2/EIdx + ∫42100x2/2EIdx
= 266.66 + 1866.6/2 = 266.66 + 933.33
For cantilever always write load from free end. For simply write load from supports.
ΔC = 1200/EI
Q14) Find slope at deflection ‘A’, deflection at ‘C’.
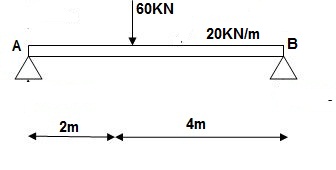
A14)
M Diagram
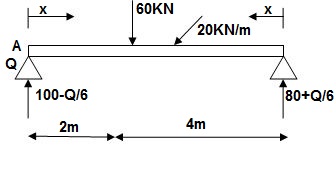
Reactions in M dia.
∑MA = VB(6) – 20 x 6 x 3 – 60(2) – Q = 0
VB = 80 + Q/6
∑Fy = VA + VB – 60 – 20 x 6 = 0
VA = 100 – Q/6
Zone Origin limits EI M ӘM/ӘQ
AC A 0 – 2 EI (100-Q/6)(x) 1 – x/6+ Q – 20(x2/2)
BC B 0 – 4 EI (80+Q/6)(x)-20x2/2 x/6
ϴA = ∫20{100(x) – 10x2}{1-x/6}dx/dEI + ∫40{80x – 10x2}x/6dx/EI
= 1/EI{135.55 + 177.78}

∑MA = VB(6) – 20(6)(3) – (60 + Q)2 = 0
VB = 80 + Q/3
∑Fy = VA + VB – (60 + Q) – 20(6) = 0
VA = -80 – Q/3 + 60 + Q + 120 = 0
VA = 100 + 2/3Q
Q15) Find a deflection at a point C
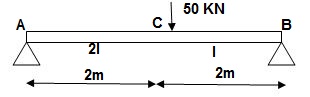
A15)
M Diagram
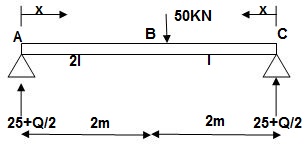
Zone Origin Limit EI MӘM/ӘQ
AC A 0 – 2 EI (25 + Q/2)x x/2
BC B 0 – 2 EI (25 + Q/2)x x/2
ΔC = ∫20(25x)x/2dx/EI + ∫2025x(x/2)dx/2EI
= 33.33 + 16.66/EI
