Unit - 1
Tachometric Surveying
Q1) What is tachometric surveying?
A1)
Tachometric surveying is a technique of angular surveying wherein the horizontal distance from the device to the group of workers stations are decided from instrumental observations only.
Thus the chaining operations are eliminated. Field Work may be finished very swiftly Tachometry is specifically used for making ready the contour plans of regions.
As chaining is avoided, as a ways as possible, this technique of surveying is excellent proper in damaged and hilly regions, regions protected with stretches of water, Swamps, etc. wherein chaining becomes very slow, tedious and inaccurate.
Tachometric surveying is a technique of angular surveying wherein the horizontal distance from the
A tachometer is much like an everyday transit theodolite geared up with stadia wires similarly to the imperative cross-hairs.
As accuracy and velocity are necessary, the telescope geared up with a tachometer need to satisfy extra requirements. Also, the vertical circle have to be greater refined.
The telescope of the tachometer is commonly longer than that of the Ordinary theodolite and has a better strength of magnification. The item glass is of extra diameter, and the lens machine is of higher quality. The magnification strength have to now no longer be much less than 20-25.
This precept is utilized in special techniques in special ways.
Mainly there are techniques of tachometry survey.
(1) Stadia machine, and
(2) Tangential machine.
Q2) What are the methods of tachometric surveying?
A2)
1. Stadia System of Tachometry:
In the stadia machine, the horizontal distance to the team of workers Station from the tool station and the elevation of the team of workers station regarding the road of sight of the tool is received with best one commentary from the tool Station. In the stadia technique, there are specially structures of surveying.
(1) Constant hair technique and,
(2) Movable hair technique.
i. Fixed Hair Method:
In the constant hair technique of tachometric surveying, the tool hired for taking observations encompass a telescope geared up with extra horizontal go hairs one above and the alternative underneath the critical hair.
These are located equidistant from the critical hair and are known as stadia hairs.
When a team of workers is considered via the telescope, the stadia hairs are visible to intercept a sure period of the team of workers, and this varies immediately with the space among the tool and the stations.
As the space among the stadia hair is constant, this technique is known as the “constant hair technique.”
Ii. Movable Hair Method;
In the movable Hair technique of tachometric surveying, the tool used for taking observations encompass a telescope geared up with stadia hairs which may be moved and stuck at any distance from the critical hair (in the limits of the diaphragm).
The team of workers used with this tool includes objectives (marks) at a set distance apart (say 3.four mm).
The Stadia c language that's variable for the special positions of the team of workers is measured, and the horizontal distance from the tool station to the team of workers station is computed.
2. Tangential System of Tachometric Surveying:
In this machine of tachometric surveying, observations might be important from the tool station to the team of workers station to decide the horizontal distance and the distinction with inside the elevation among the road of collimation and the team of workers station.
The best gain of this technique is this survey may be carried out with everyday transit theodolite.
As the everyday transit theodolite are inexpensive than the difficult and greater delicate tachometer, so, the survey might be greater economical.
So, as some distance the discount of discipline notes, distances and elevations are worried there isn't plenty distinction among those structures.
But this machine is taken into consideration not as good as the stadia machine because of the subsequent motives and may be very seldom used nowadays.
This entails size of vertical angles, and the tool might also additionally get disturbed among the 2 observations.
The pace is decreased because of greater range of observations and the adjustments with inside the atmospheric situations will have an effect on the readings considerably.
The team of workers used on this technique is much like the only hired with inside the movable hair technique of stadia surveying. The distance among the objectives or vanes can be 3-4 m.
Q3) Explain principal of stadia method
A3)
Spaced both aspect of it. These stadia traces outline the constant parallaxes attitude.
If the theodolite telescope is sighted directly to a levelling personnel and the readings of the outer traces noted, the distinction with inside the readings, the personnel intercept (s), may be immediately proportional to the horizontal distance among the device and the personnel.
Generally, the gap among the stadia traces is designed in this type of way that the horizontal distance Z>H among the device and personnel is given through: wherein Z) s= slope distance, and 0=vertical attitude measured through the theodolite.
Therefore: wherein swabs = distinction in peak among A and B, h, = peak of device (trunnion axis to ground), m = center hair studying, and V= distinction in peak among center-hair studying and grunion axis = 50s sin 20 (6. 11)
Several self-decreasing tachometers have additionally been designed.
The major gain of those gadgets is their capacity to make amends for the impact of the inclination of the theodolite telescope and, hence, permit the direct willpower of horizontal distance without extra computation.
Two outstanding examples of this form of device are the Wild RDS vertical personnel self-decreasing tachometer and the Kern DK-RT horizontal bar double-photograph self-decreasing tachometer.
Details of the development and use of those gadgets can be observed in Hodges and Greenwood, five and Smith.6 In latest years, the manufacture of those particular optical gadgets has ceased, their location being taken through low-price digital measuring gadgets.
Q4) What is sub tense bar?
A4)
The 2d approach (constant base, variable attitude) is normally called the sub tense or horizontal sub tense bar technique.
The technique is generally restricted to the size of distance for manage purposes. Using this approach, distances can be decided with a proportional blunders of as much as 1/10000. The instrumentation required includes a sub tense bar, generally 2 m long, and a one-2d theodolite, consisting of the Wild T2.
The bar has goals established at every give up of an invar strip. The strip is covered through a surrounding aluminum strip which will make sure that, for all sensible purposes, the duration of the bar stays consistent at 2 m.
The bar is installation and orientated at proper angles to the road of sight of the theodolite
Tachometry is a department of surveying wherein the horizontal and vertical distances are decided via way of means of angular observations with a tachometer, the chaining operation being altogether removed
Tachometry isn't as correct as is changing, however it's far a long way extra fast in tough and tough use wherein levelling is tedious and chaining is each misguided and slow.
Thus it's far high-quality proper whilst boundaries together with steep and damaged ground, deep ravines, stretches of water or swamps are met with Tachometry is specially used even as getting ready contour plans and traversing and is likewise appropriate for hydrographic surveys, vicinity surveys of roads, railways, etc.
It is likewise once in a while hired for small surveys wherein elevations aren't decided.
Q5) Explain theory of analytic lens
A5)
Analytic lens is a further lens used with inside the device. It is a unique lens that's located among the item glass and the eyepiece of the telescope on the way to put off the additive consistent (f+d).
This is executed to make the expression for the space among device station and workforce role extra simplified.
Tachometry is a department of angular surveying wherein the horizontal and vertical distances of factors are received with the aid of using instrumental observation. The device normally hired in tachometry is a tachometer and a levelling workforce.
A tachometer in a popular sense, is a transit Theodolite having a stadia telescope i.e. a telescope equipped with a stadia diaphragm, i.e. a telescope prepared with horizontal hairs referred to as stadia hairs further to the everyday cross- hairs.
The values of f/i and (f+d) are normally marked on a card connected to the interior of field with the aid of using the maker.
Multiplying consistent price is normally one hundred and additive consistent (f+d) price various from 30 to 60 cm with inside the case of an outside focusing telescope and with inside the case of an inner focusing telescope it varies from eight to twenty cm.
The item of presenting a further convex lens, referred to as an analytic lens, with inside the telescope is to put off the additive consistent (f+d). That means (f+d) might be zero.
Stadia metric range finding, or the stadia approach, is a way of measuring distances with a telescopic instrument.
The time period stadia comes from a Greek unit of period Station (identical to six hundred Greek toes, opus) which became the everyday period of a sports activities stadium of the time.
Stadia metric range finding is used for surveying and with inside the telescopic points of interest of firearms, artillery pieces, or tank guns, in addition to a few binoculars and different optics.
It remains extensively utilized in long-variety army sniping, however in lots of expert programs it's far being changed with microwave, infrared, or laser range finding methods.
Although a whole lot simpler to use, digital rangefinders can supply away the shooter's role to a well-geared up adversary, and the want for correct variety estimation existed for a whole lot longer than digital rangefinders small and rugged sufficient to be appropriate for army use.
The stadia approach is primarily based totally upon the precept of comparable triangles. This way that, for a triangle with a given attitude, the ratio of contrary facet period to adjoining facet period (tangent) is constant.
By the use of a reticle with marks of an acknowledged angular spacing, the precept of comparable triangles may be used to locate both the gap to gadgets of acknowledged length and the dimensions of gadgets at an acknowledged distance.
In both case, the acknowledged parameter is used, together with the angular measurement, to derive the period of the alternative facet.
Since a radian is described because the attitude fashioned while the period of a round arc equals the radius of the circle, a mill radian is the attitude fashioned while the period of a round arc equals 1/a thousand of the radius of the circle.
For telescopic angles, the approximations of substantially simplify the trigonometry, permitting one to scale gadgets measured in mill radians through a telescope through an element of a thousand for distance or height.
An item five meters excessive, for example, will cowl 1 mad at 5000 meters, or five mad at a thousand meters, or 25 mad at 2 hundred meters.
Since the radian expresses a ratio, it's far impartial of the gadgets used; an item 6 toes excessive overlaying 1 mad could be 6000 toes distant. In practice, it is able to be visible that tough approximations can be made with a proper triangle whose base (b) is identical to the gap of the 'rangefinder' from the eye; with the aperture (a) being the hollow through which the goal is sighted – the apex of this triangle being at the floor of the user's eye.
Q6) Explain various terms used in tachometric surveying?
A6)
Height and Distance
It is an important application of trigonometry which helps us to find the height of any object and distance of that object from any point which are not directly measurable. If the angle of elevation/depression from a point is known.
Line of Sight
A line of sight is the line drawn from the eye of an observer to the point, where the object is viewed by the observer.
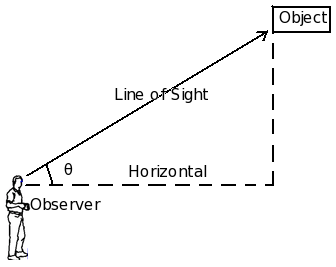
Fig. Angle of elevation
In this diagram, marks the angle of elevation of the top of the object as seen from a point on the ground.
Horizontal Line
The line of sight which is parallel to ground level is known as horizontal line.
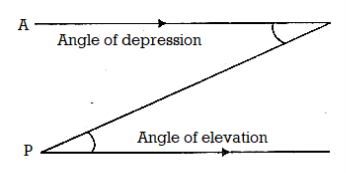
Angle of Elevation
The angle of elevation of the point viewed is the angle formed by the line of sight with the horizontal, when the point being viewed is above the horizontal level.
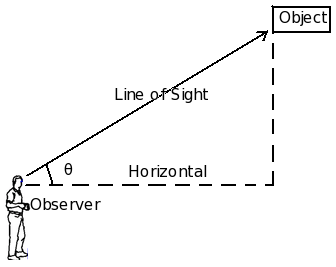
Fig. Angle of elevation
As shown in the diagram above, an observer is looking at an object located above the horizontal axis. In this process, it makes an angle with the x-axis. This angle is called angle of elevation.
Understanding the angle of elevation formula:
The angle of elevation formula helps to solve the angle of elevation problems very easily. As it is visible from the figure, the vertical from object makes a right angle with the horizontal. So if we know the height of the object and the linear distance, we can easily find out the angle by trigonometric formula. It is given by tan = Height / distance. The angle of elevation of the sun that is better known as altitude angle, can also be found by the same method.
Angle of Depression
When the line of sight is below the horizontal level, the angle so formed by the line of sight with the horizontal is called the angle of depression.
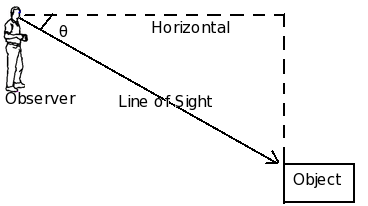
Fig. Angle of depression θ
As shown, an observer is looking at the downwards object while making an angle with the horizontal axis. Here θ can be called the angles of depression for an observer.
Height and Distance: One of the main application of trigonometry is to find the distance between two or more than two places or to find the height of the object or the angle subtended by any object at a given point without actually measuring the distance or heights or angles. Trigonometry is useful to astronomers, navigators, architects and surveyors etc. in solving problems related to heights and distances.
Height and Distance
The directions of the objects can be described by measuring:
- Angle of elevation
- Angle of depression
Angles of elevation or angles of depression of the objects are measured by an instrument called Theodolite. Theodolite is based on the principles of trigonometry, which is used for measuring angles with a rotating telescope. In 1856, Sir George Everest first used the giant theodolite, which is now on display in the Museum of the survey of India in Dehradun
Angle of Elevation
Let P be the position of the object above the horizontal line OA and O be the eye of the observer, then angle AOP is called angle of elevation. It is called the angle of elevation, because the observer has to elevate (raise) his line of sight from the horizontal OA to see the object P. [When the eye turns upwards above the horizontal line].
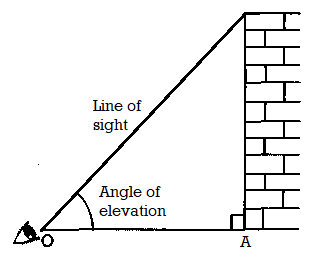
Line of sight: It is the line drawn from the eye of an observer to the object viewed.
Q7) What is angle of depression?
A7)
Angle of Depression
Let P be the position of the object below the horizontal line OA and O be the eye of the observer, then angle AOP is called angle of depression.
It is called the angle of depression because the observer has to depress (lower) his line of sight from the horizontal OA to see the object P.
Below the eye level: If the object lies below the horizontal plane of our eyes, then we have to move our head downwards to view it. In doing so, our lines of sight moves downwards through an angle and the angle, which the line of sight now makes with the horizontal line, is called the angle of depression of the object from our eyes.
Example : Let OH be the horizontal line at the eye level. If a person at O looks at an object P lying below the eye level, then, ∠HOP is the angle of depression of P as seen from O.

Note: Angle of depression of P as seen from O = angle of elevation of O, as seen from P.

∴∠AOP = ∠OPH
Height and Distance Important Points
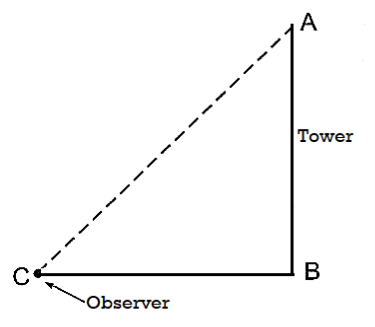
- In solving problems observer is represented by a point if his height is not given.
- In solving problems object is represented by a line segment and some times by a point if height or length is not considered.
For example, AB is tower and point C is observer.
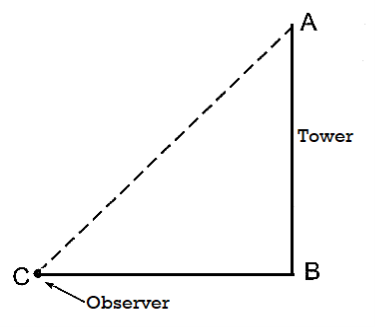
- A line drawn parallel to earth surface is called horizontal line.
- The angle of elevation and depression are always acute angles.

- If the observer moves towards the objects like tower, building, cliff, etc. then angle of elevation increases and if the observer moves away from the object, the angle of elevation decreases.
- If the angle of elevation of sun decreases, then the length of shadow of an object increases and vice-versa.
- If in problems, the angle of elevation of an object is given, then we conclude that the object is at higher altitude than observer. The angle of depression implies that observer is at higher altitude than object.
Q8) Explain Height and Distance Questions
A8)
1. If a pole 6 m high casts a shadow 2√3 m long on the ground, find the Sun’s elevation.
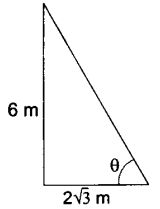
Tan θ = 
θ = 60o
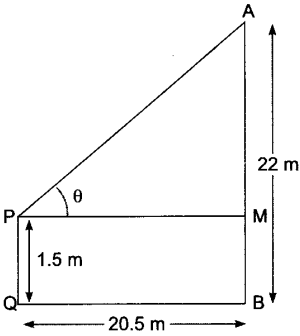
2. An observer 1.5 m tall is 20.5 m away from a tower 22 m high. Determine the angle of elevation of the top of the tower from the eye of the observer.
PQ = MQ = 1.5 m
AM = AB – MB = 22 – 1.5 = 20.5 m
Now in APM
Tan θ = AM/PM
= 20.5/20.5 = 1
= 45o
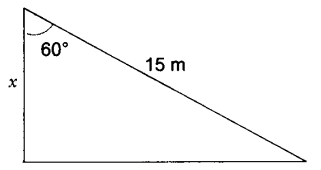
3. A ladder 15 m long makes an angle of 60o with the wall. Find the height of the point where the ladder touches the wall.
Cos 60o = x/15
½ = x/15 x = 15/2 m = 7.5 m
4. The ratio of the height of a tower and the length of its shadow on the ground is √3 : 1. What is the angle of elevation of the sun?
Given: AB/BC = 3/1
Then, tan θ = AB/BC = 3
θ = 60o
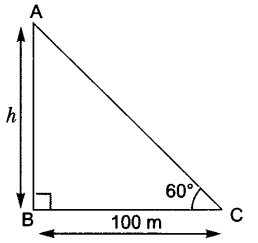
5. If the angle of elevation of a tower from a distance of 100 m from its foot is 60°, then what will be the height of the tower?
Let h be the height of the tower.
Tan 60o = AB/BC
3 = h/100
h = 103 m.
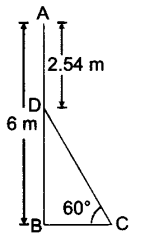
6. In Fig., AB is a 6 m high pole and CD is a ladder inclined at an angle of 60° to the horizontal and reaches up to a point D of pole. If AD = 2.54 m, find the length of the ladder, (use √3 =1.73)
DB = (6 – 2.54)m = 3.46 m
In BDC, sin 60o = BD/CD
3/2 = 3.46/CD CD = (3.46 2)/1.73
DC = 4 m
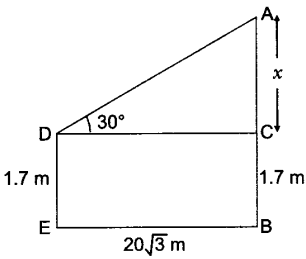
7. An observer, 1.7 m tall, is 20 √3 m away from a tower. The angle of elevation from the eye of observer to the top of tower is 30°. Find the height of tower.
Let AB be the height of tower and DE be the height of observer.
Then in ACD, AC/DC = tan 30o
x/203 = tan 30o = 1/3 x = 20 m
AB = 20 + 1.7 = 21.7 m
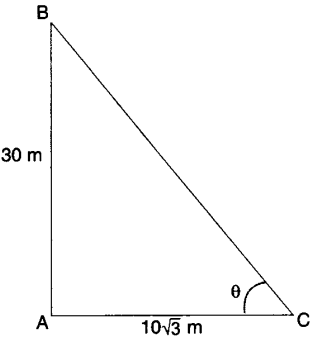
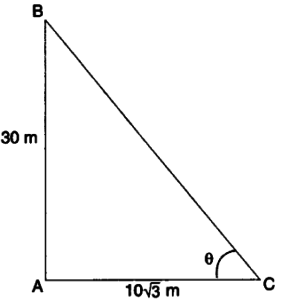
8. If a tower 30 m high, casts a shadow 10 √3 m long on the ground, then what is the angle of elevation of the sun?
In ABC
Tan θ = AB/AC = 30/103 = 3
tan θ = tan 60
θ = 60o
Q8) Explain tangential method
A9)
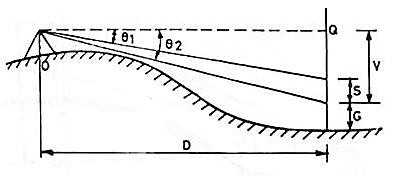
The Tangential System of Tachometry:
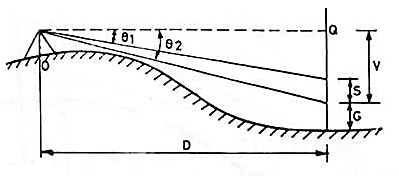
This method is used when the telescope is not fitted with a stadia diagram. In this method, the telescope is directed towards the staff to which the horizontal and vertical distances are to be measured and two vertical angles to two vanes or targets on the staff at a known distance (S) apart are taken.
The horizontal and vertical distances are then calculated as follows:
Case 1:
When both the observed angles are angles of elevation:
O=the instruments station.
O’=the position of the instruments axis
P= the staff station.
∠AO’Q= θ1= vertical angle to the upper vane.
∠BO’Q= θ2 =” “ “ lower
AB=S=the staff intercept.
BQ=V= the horizontal distance from the inst, axis to the lower vane.
O’Q=D= the horizontal distance from the inst. Station O to the staff station P
PB= h= the height of the lower vane above the foot of the staff.
BQ = V = D tan θ2
S = D(tan θ1 – tan θ2)
D = S/(tan θ1 – tan θ2) ……..Eqn 10.13
And V = D tan θ2 = S tan θ2/(tan θ1 – tan θ2) …………Eqn. 10.14
R.L. Of staff station P = R.L. Of the line of sight + V – h.
Case II:
When both the observed angles are angles of depression:
S = QB – QA = D (tan θ2 – tan θ1)
D = S/(tan θ2 – tan θ1) ………….Eqn. 10.15
And V = D tan θ = S.tanθ2 /(tan θ2 – tan θ1 ) ……………..Eqn. 10.16
R.L. Of staff stn. P = R.L. Of the line of sight - V - h
Case III
When one of the observed angle is the angle of elevation and the other an angle of depression:

S = AC = AB + BC = D (tan θ1 + tan θ2)
D = S /(tan θ1 + tan θ2) …………Eqn. 10.17
And V = D tan θ2 = Stan θ2/(tan θ1 + tan θ2) ………..Eqn. 10.18
R.I. Of staff station = R.I. Of line of sight – V - h
Q9) What is sub tense bar measurements?
A10)
A subtense bar is a horizontal staff with targets fixed at a known distance apart. It is about 4m long having a small spirit level and a quick levelling head.
A sight rule, provided at its centre, can be placed along the line of sight by viewing the telescope of the theodolite thought the vanes. The bar is mounted on a tripod and is placed at right angles to the line of sight for making observations. After levelling and aligning, it is clamped by means of clamp screw.
The targets, made of discs of about 20 cm diameter are painted red on one side, and white on the other. The centres of body the sides of the targets are painted black in 7.5 cm diameter. The targets are placed at a distance of 2.5 m and 3 m. When the targets are placed 2.5 m apart, the white faces are to face the instrument and when they are placed 3m apart, the red faces face the instrument.
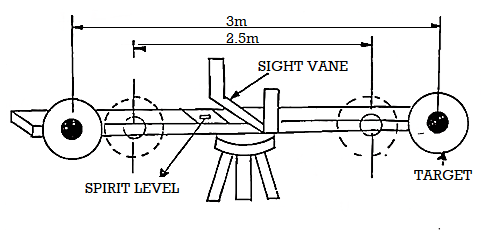
The horizontal and vertical angles are measured with a transit theodolite. For measuring vertical angles the method will be similarly to the movable hair method of stadia tacheometry and the distances are similarly deduced. For measuring horizontal angles, subtended at the instrument station by the two targets, the method of repetition is used, the horizontal distance.
D between the instrument station and the subtense bar station is found as follows:
Let O= the position of the instrument for measuring the horizontal angle 0 by the horizontal circle of theodolite.
AB= horizontal base of a length S.

If line AB is perpendicular to OC, where C is midway between A and B, then from triangle OAC,
D = ½ S cot θ/2
Or D = S/(2 tan θ/2) ……..(i)
If θ is small, then
Tan θ/2 = θ/2, where θ is in raians
= ½ . θ/206265 if θ is in seconds.
(1 radian = 206265 seconds).
Putting this value in (i) above, we get
D = (S 206265)/θ ……..(ii)
Q10) Explain Levelling by Stadia
A11)
Levelling by stadia tachometry is an indirect and rapid method of levelling. It is suitable where country is rough and the precision needed is not great. The transit should preferably be provided with a sensitive control level for the vertical vernier so that the error may be readily eliminated.
The method of running a line of levels by this method is as follows:
(i) Set up the transit at a convenient point.
(ii) Take a back sight on the staff held at a B.M., first by observing the stadia interval and then by measuring the vertical angle to some arbitrarily chosen mark on the staff.
(iii) Establish a change point in advance of the transit, and take similar observations, the vertical angle being measured with horizontal cross-hari set on the same mark as before.
(iv) Move the trait to a new point in advance of the change point and repeat the process.
(v) Record the stadia distance and vertical angles and also the staff reading which is used as an index when vertical angles are measured.
The objectives, product of discs of approximately 20 cm diameter are painted crimson on one side, and white at the other.
The centers of frame the perimeters of the objectives are painted black in 7.five cm diameter. The objectives are positioned at a distance of 2.five m and three m. When the objectives are positioned 2.5 m apart, the white faces are to stand the tool and while they're positioned 3m apart, the crimson faces face the tool.
Sub tense Bar
The horizontal and vertical angles are measured with a transit theodolite. For measuring vertical angles the technique might be further to the movable hair technique of stadia tachometry and the distances are further deduced. For measuring horizontal angles, subtended on the tool station via way of means of the 2 objectives, the technique of repetition is used, the horizontal distance.
D among the tool station and the sub tense bar station is located as follows:
Let
O= the location of the tool for measuring the horizontal perspective zero via way of means of the horizontal circle of theodolite.
AB= horizontal base of a period S. Levelling via way of means of Stadia: Levelling via way of means of stadia tachometry is an oblique and fast technique of levelling.
It is appropriate wherein U. S. Is difficult and the precision wanted isn't always great.
The transit need to rather be supplied with a touchy manage degree for the vertical dernier in order that the mistake can be effortlessly eliminated. The technique of walking a line of degrees via way of means of this technique is as follows:
(i) Set up the transit at a handy factor.
(ii) Take a again sight at the personnel held at a B.M., first via way of means of watching the stadia c language after which via way of means of measuring the vertical perspective to a few arbitrarily selected mark at the personnel.
(iii) Establish an alternate factor earlier of the transit, and take comparable observations, the vertical perspective being measured with horizontal cross-hari set at the identical mark as before.
(iv) Move the trait to a brand new factor earlier of the alternate factor and repeat the process.
(v) Record the stadia distance and vertical angles and additionally the personnel studying that's used as an index while vertical angles are measured.
Q11) What are the errors in stadia surveying?
A12)
Errors and Precautions in Tachometric Surveying:
- The defects can be technical faults resulting from deception and seeing, or herbal causes.
- Imperfect everlasting modifications with inside the tool and wrong graduations at the stadia rod can cause the instrumental mistakes.
- Before beginning the research, whilst the tool is in complete everlasting adjustment, the constants of the tool furnished via way of means of the producer have to be showed via way of means of real remark with inside the area.
- It is specifically applicable for vital surveys in which the maximum sizeable parameter is precision (and now no longer the time).
- The graduations at the rod have to be carefully checked and vital changes have to be made to the measured measurements if a few distinction is found.
- The mistakes springing up from manipulation and recognizing depend upon the surveyor’s productiveness and abilities.
- Which are prompted via way of means of insufficient tool centering and lowering, and faulty readings of the Stadia? There have to be no Parallax to certainly see the stadia pin.
- When taking stadia hair readings, warning may be taken to look if the axial hair isn't pressured for stadia hair.
- The precision of stadia hair readings may be examined via way of means of seeing if the imply of stadia hair readings is equal to axial hair reading.
- Wind, unequal enlargement of the tool components, and visibility and unequal refraction can purpose mistakes because of herbal causes.
- The maximum vital of those is the second.
- This is attributed to the differential refraction of mild rays via way of means of transferring through numerous strain layers of soil.
- Therefore, so one can save you this mistake, noon readings could be stopped to the diploma practicable.
- The most allowable hole with inside the distance is 1 in 500 to at least one in 900 and in elevations 0.08 to 0.10 m.
- Always, the sightlines want now no longer be beneath a meter from the level.
- The final blunders in a traverse of the tachometry does now no longer surpass 0. LIFE, in which p is the meter diameter of the traverse.
Unit - 1
Tachometric Surveying
Q1) What is tachometric surveying?
A1)
Tachometric surveying is a technique of angular surveying wherein the horizontal distance from the device to the group of workers stations are decided from instrumental observations only.
Thus the chaining operations are eliminated. Field Work may be finished very swiftly Tachometry is specifically used for making ready the contour plans of regions.
As chaining is avoided, as a ways as possible, this technique of surveying is excellent proper in damaged and hilly regions, regions protected with stretches of water, Swamps, etc. wherein chaining becomes very slow, tedious and inaccurate.
Tachometric surveying is a technique of angular surveying wherein the horizontal distance from the
A tachometer is much like an everyday transit theodolite geared up with stadia wires similarly to the imperative cross-hairs.
As accuracy and velocity are necessary, the telescope geared up with a tachometer need to satisfy extra requirements. Also, the vertical circle have to be greater refined.
The telescope of the tachometer is commonly longer than that of the Ordinary theodolite and has a better strength of magnification. The item glass is of extra diameter, and the lens machine is of higher quality. The magnification strength have to now no longer be much less than 20-25.
This precept is utilized in special techniques in special ways.
Mainly there are techniques of tachometry survey.
(1) Stadia machine, and
(2) Tangential machine.
Q2) What are the methods of tachometric surveying?
A2)
1. Stadia System of Tachometry:
In the stadia machine, the horizontal distance to the team of workers Station from the tool station and the elevation of the team of workers station regarding the road of sight of the tool is received with best one commentary from the tool Station. In the stadia technique, there are specially structures of surveying.
(1) Constant hair technique and,
(2) Movable hair technique.
i. Fixed Hair Method:
In the constant hair technique of tachometric surveying, the tool hired for taking observations encompass a telescope geared up with extra horizontal go hairs one above and the alternative underneath the critical hair.
These are located equidistant from the critical hair and are known as stadia hairs.
When a team of workers is considered via the telescope, the stadia hairs are visible to intercept a sure period of the team of workers, and this varies immediately with the space among the tool and the stations.
As the space among the stadia hair is constant, this technique is known as the “constant hair technique.”
Ii. Movable Hair Method;
In the movable Hair technique of tachometric surveying, the tool used for taking observations encompass a telescope geared up with stadia hairs which may be moved and stuck at any distance from the critical hair (in the limits of the diaphragm).
The team of workers used with this tool includes objectives (marks) at a set distance apart (say 3.four mm).
The Stadia c language that's variable for the special positions of the team of workers is measured, and the horizontal distance from the tool station to the team of workers station is computed.
2. Tangential System of Tachometric Surveying:
In this machine of tachometric surveying, observations might be important from the tool station to the team of workers station to decide the horizontal distance and the distinction with inside the elevation among the road of collimation and the team of workers station.
The best gain of this technique is this survey may be carried out with everyday transit theodolite.
As the everyday transit theodolite are inexpensive than the difficult and greater delicate tachometer, so, the survey might be greater economical.
So, as some distance the discount of discipline notes, distances and elevations are worried there isn't plenty distinction among those structures.
But this machine is taken into consideration not as good as the stadia machine because of the subsequent motives and may be very seldom used nowadays.
This entails size of vertical angles, and the tool might also additionally get disturbed among the 2 observations.
The pace is decreased because of greater range of observations and the adjustments with inside the atmospheric situations will have an effect on the readings considerably.
The team of workers used on this technique is much like the only hired with inside the movable hair technique of stadia surveying. The distance among the objectives or vanes can be 3-4 m.
Q3) Explain principal of stadia method
A3)
Spaced both aspect of it. These stadia traces outline the constant parallaxes attitude.
If the theodolite telescope is sighted directly to a levelling personnel and the readings of the outer traces noted, the distinction with inside the readings, the personnel intercept (s), may be immediately proportional to the horizontal distance among the device and the personnel.
Generally, the gap among the stadia traces is designed in this type of way that the horizontal distance Z>H among the device and personnel is given through: wherein Z) s= slope distance, and 0=vertical attitude measured through the theodolite.
Therefore: wherein swabs = distinction in peak among A and B, h, = peak of device (trunnion axis to ground), m = center hair studying, and V= distinction in peak among center-hair studying and grunion axis = 50s sin 20 (6. 11)
Several self-decreasing tachometers have additionally been designed.
The major gain of those gadgets is their capacity to make amends for the impact of the inclination of the theodolite telescope and, hence, permit the direct willpower of horizontal distance without extra computation.
Two outstanding examples of this form of device are the Wild RDS vertical personnel self-decreasing tachometer and the Kern DK-RT horizontal bar double-photograph self-decreasing tachometer.
Details of the development and use of those gadgets can be observed in Hodges and Greenwood, five and Smith.6 In latest years, the manufacture of those particular optical gadgets has ceased, their location being taken through low-price digital measuring gadgets.
Q4) What is sub tense bar?
A4)
The 2d approach (constant base, variable attitude) is normally called the sub tense or horizontal sub tense bar technique.
The technique is generally restricted to the size of distance for manage purposes. Using this approach, distances can be decided with a proportional blunders of as much as 1/10000. The instrumentation required includes a sub tense bar, generally 2 m long, and a one-2d theodolite, consisting of the Wild T2.
The bar has goals established at every give up of an invar strip. The strip is covered through a surrounding aluminum strip which will make sure that, for all sensible purposes, the duration of the bar stays consistent at 2 m.
The bar is installation and orientated at proper angles to the road of sight of the theodolite
Tachometry is a department of surveying wherein the horizontal and vertical distances are decided via way of means of angular observations with a tachometer, the chaining operation being altogether removed
Tachometry isn't as correct as is changing, however it's far a long way extra fast in tough and tough use wherein levelling is tedious and chaining is each misguided and slow.
Thus it's far high-quality proper whilst boundaries together with steep and damaged ground, deep ravines, stretches of water or swamps are met with Tachometry is specially used even as getting ready contour plans and traversing and is likewise appropriate for hydrographic surveys, vicinity surveys of roads, railways, etc.
It is likewise once in a while hired for small surveys wherein elevations aren't decided.
Q5) Explain theory of analytic lens
A5)
Analytic lens is a further lens used with inside the device. It is a unique lens that's located among the item glass and the eyepiece of the telescope on the way to put off the additive consistent (f+d).
This is executed to make the expression for the space among device station and workforce role extra simplified.
Tachometry is a department of angular surveying wherein the horizontal and vertical distances of factors are received with the aid of using instrumental observation. The device normally hired in tachometry is a tachometer and a levelling workforce.
A tachometer in a popular sense, is a transit Theodolite having a stadia telescope i.e. a telescope equipped with a stadia diaphragm, i.e. a telescope prepared with horizontal hairs referred to as stadia hairs further to the everyday cross- hairs.
The values of f/i and (f+d) are normally marked on a card connected to the interior of field with the aid of using the maker.
Multiplying consistent price is normally one hundred and additive consistent (f+d) price various from 30 to 60 cm with inside the case of an outside focusing telescope and with inside the case of an inner focusing telescope it varies from eight to twenty cm.
The item of presenting a further convex lens, referred to as an analytic lens, with inside the telescope is to put off the additive consistent (f+d). That means (f+d) might be zero.
Stadia metric range finding, or the stadia approach, is a way of measuring distances with a telescopic instrument.
The time period stadia comes from a Greek unit of period Station (identical to six hundred Greek toes, opus) which became the everyday period of a sports activities stadium of the time.
Stadia metric range finding is used for surveying and with inside the telescopic points of interest of firearms, artillery pieces, or tank guns, in addition to a few binoculars and different optics.
It remains extensively utilized in long-variety army sniping, however in lots of expert programs it's far being changed with microwave, infrared, or laser range finding methods.
Although a whole lot simpler to use, digital rangefinders can supply away the shooter's role to a well-geared up adversary, and the want for correct variety estimation existed for a whole lot longer than digital rangefinders small and rugged sufficient to be appropriate for army use.
The stadia approach is primarily based totally upon the precept of comparable triangles. This way that, for a triangle with a given attitude, the ratio of contrary facet period to adjoining facet period (tangent) is constant.
By the use of a reticle with marks of an acknowledged angular spacing, the precept of comparable triangles may be used to locate both the gap to gadgets of acknowledged length and the dimensions of gadgets at an acknowledged distance.
In both case, the acknowledged parameter is used, together with the angular measurement, to derive the period of the alternative facet.
Since a radian is described because the attitude fashioned while the period of a round arc equals the radius of the circle, a mill radian is the attitude fashioned while the period of a round arc equals 1/a thousand of the radius of the circle.
For telescopic angles, the approximations of substantially simplify the trigonometry, permitting one to scale gadgets measured in mill radians through a telescope through an element of a thousand for distance or height.
An item five meters excessive, for example, will cowl 1 mad at 5000 meters, or five mad at a thousand meters, or 25 mad at 2 hundred meters.
Since the radian expresses a ratio, it's far impartial of the gadgets used; an item 6 toes excessive overlaying 1 mad could be 6000 toes distant. In practice, it is able to be visible that tough approximations can be made with a proper triangle whose base (b) is identical to the gap of the 'rangefinder' from the eye; with the aperture (a) being the hollow through which the goal is sighted – the apex of this triangle being at the floor of the user's eye.
Q6) Explain various terms used in tachometric surveying?
A6)
Height and Distance
It is an important application of trigonometry which helps us to find the height of any object and distance of that object from any point which are not directly measurable. If the angle of elevation/depression from a point is known.
Line of Sight
A line of sight is the line drawn from the eye of an observer to the point, where the object is viewed by the observer.
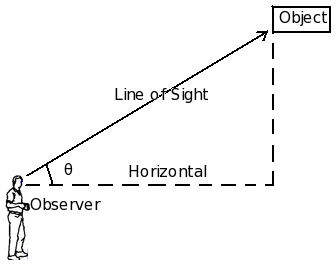
Fig. Angle of elevation
In this diagram, marks the angle of elevation of the top of the object as seen from a point on the ground.
Horizontal Line
The line of sight which is parallel to ground level is known as horizontal line.
Angle of Elevation
The angle of elevation of the point viewed is the angle formed by the line of sight with the horizontal, when the point being viewed is above the horizontal level.

Fig. Angle of elevation
As shown in the diagram above, an observer is looking at an object located above the horizontal axis. In this process, it makes an angle with the x-axis. This angle is called angle of elevation.
Understanding the angle of elevation formula:
The angle of elevation formula helps to solve the angle of elevation problems very easily. As it is visible from the figure, the vertical from object makes a right angle with the horizontal. So if we know the height of the object and the linear distance, we can easily find out the angle by trigonometric formula. It is given by tan = Height / distance. The angle of elevation of the sun that is better known as altitude angle, can also be found by the same method.
Angle of Depression
When the line of sight is below the horizontal level, the angle so formed by the line of sight with the horizontal is called the angle of depression.
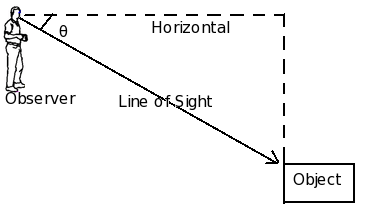
Fig. Angle of depression θ
As shown, an observer is looking at the downwards object while making an angle with the horizontal axis. Here θ can be called the angles of depression for an observer.
Height and Distance: One of the main application of trigonometry is to find the distance between two or more than two places or to find the height of the object or the angle subtended by any object at a given point without actually measuring the distance or heights or angles. Trigonometry is useful to astronomers, navigators, architects and surveyors etc. in solving problems related to heights and distances.
Height and Distance
The directions of the objects can be described by measuring:
- Angle of elevation
- Angle of depression
Angles of elevation or angles of depression of the objects are measured by an instrument called Theodolite. Theodolite is based on the principles of trigonometry, which is used for measuring angles with a rotating telescope. In 1856, Sir George Everest first used the giant theodolite, which is now on display in the Museum of the survey of India in Dehradun
Angle of Elevation
Let P be the position of the object above the horizontal line OA and O be the eye of the observer, then angle AOP is called angle of elevation. It is called the angle of elevation, because the observer has to elevate (raise) his line of sight from the horizontal OA to see the object P. [When the eye turns upwards above the horizontal line].
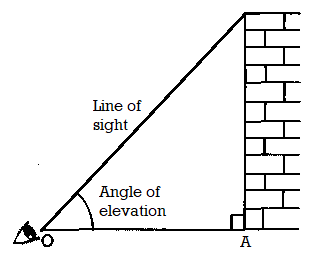
Line of sight: It is the line drawn from the eye of an observer to the object viewed.
Q7) What is angle of depression?
A7)
Angle of Depression
Let P be the position of the object below the horizontal line OA and O be the eye of the observer, then angle AOP is called angle of depression.
It is called the angle of depression because the observer has to depress (lower) his line of sight from the horizontal OA to see the object P.
Below the eye level: If the object lies below the horizontal plane of our eyes, then we have to move our head downwards to view it. In doing so, our lines of sight moves downwards through an angle and the angle, which the line of sight now makes with the horizontal line, is called the angle of depression of the object from our eyes.
Example : Let OH be the horizontal line at the eye level. If a person at O looks at an object P lying below the eye level, then, ∠HOP is the angle of depression of P as seen from O.
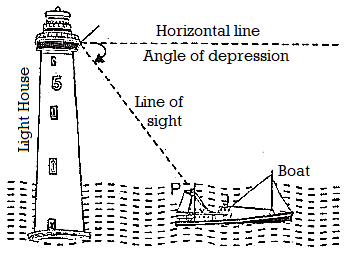
Note: Angle of depression of P as seen from O = angle of elevation of O, as seen from P.
∴∠AOP = ∠OPH
Height and Distance Important Points
- In solving problems observer is represented by a point if his height is not given.
- In solving problems object is represented by a line segment and some times by a point if height or length is not considered.
For example, AB is tower and point C is observer.
- A line drawn parallel to earth surface is called horizontal line.
- The angle of elevation and depression are always acute angles.
- If the observer moves towards the objects like tower, building, cliff, etc. then angle of elevation increases and if the observer moves away from the object, the angle of elevation decreases.
- If the angle of elevation of sun decreases, then the length of shadow of an object increases and vice-versa.
- If in problems, the angle of elevation of an object is given, then we conclude that the object is at higher altitude than observer. The angle of depression implies that observer is at higher altitude than object.
Q8) Explain Height and Distance Questions
A8)
1. If a pole 6 m high casts a shadow 2√3 m long on the ground, find the Sun’s elevation.

Tan θ = 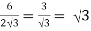
θ = 60o
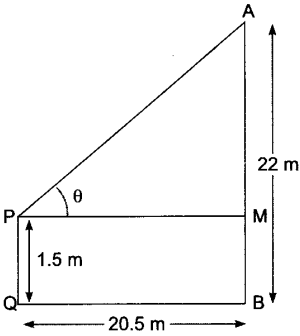
2. An observer 1.5 m tall is 20.5 m away from a tower 22 m high. Determine the angle of elevation of the top of the tower from the eye of the observer.
PQ = MQ = 1.5 m
AM = AB – MB = 22 – 1.5 = 20.5 m
Now in APM
Tan θ = AM/PM
= 20.5/20.5 = 1
= 45o
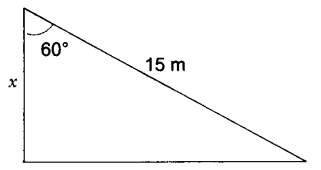
3. A ladder 15 m long makes an angle of 60o with the wall. Find the height of the point where the ladder touches the wall.
Cos 60o = x/15
½ = x/15 x = 15/2 m = 7.5 m
4. The ratio of the height of a tower and the length of its shadow on the ground is √3 : 1. What is the angle of elevation of the sun?
Given: AB/BC = 3/1
Then, tan θ = AB/BC = 3
θ = 60o
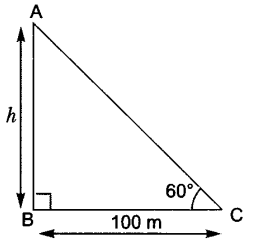
5. If the angle of elevation of a tower from a distance of 100 m from its foot is 60°, then what will be the height of the tower?
Let h be the height of the tower.
Tan 60o = AB/BC
3 = h/100
h = 103 m.
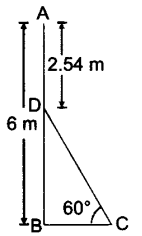
6. In Fig., AB is a 6 m high pole and CD is a ladder inclined at an angle of 60° to the horizontal and reaches up to a point D of pole. If AD = 2.54 m, find the length of the ladder, (use √3 =1.73)
DB = (6 – 2.54)m = 3.46 m
In BDC, sin 60o = BD/CD
3/2 = 3.46/CD CD = (3.46 2)/1.73
DC = 4 m
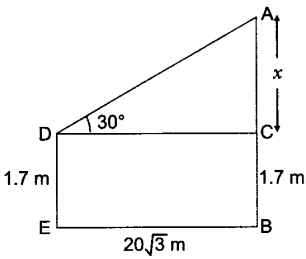
7. An observer, 1.7 m tall, is 20 √3 m away from a tower. The angle of elevation from the eye of observer to the top of tower is 30°. Find the height of tower.
Let AB be the height of tower and DE be the height of observer.
Then in ACD, AC/DC = tan 30o
x/203 = tan 30o = 1/3 x = 20 m
AB = 20 + 1.7 = 21.7 m
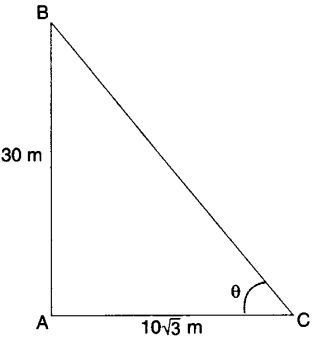
8. If a tower 30 m high, casts a shadow 10 √3 m long on the ground, then what is the angle of elevation of the sun?
In ABC
Tan θ = AB/AC = 30/103 = 3
tan θ = tan 60
θ = 60o
Q8) Explain tangential method
A9)
The Tangential System of Tachometry:
This method is used when the telescope is not fitted with a stadia diagram. In this method, the telescope is directed towards the staff to which the horizontal and vertical distances are to be measured and two vertical angles to two vanes or targets on the staff at a known distance (S) apart are taken.
The horizontal and vertical distances are then calculated as follows:
Case 1:
When both the observed angles are angles of elevation:
O=the instruments station.
O’=the position of the instruments axis
P= the staff station.
∠AO’Q= θ1= vertical angle to the upper vane.
∠BO’Q= θ2 =” “ “ lower
AB=S=the staff intercept.
BQ=V= the horizontal distance from the inst, axis to the lower vane.
O’Q=D= the horizontal distance from the inst. Station O to the staff station P
PB= h= the height of the lower vane above the foot of the staff.
BQ = V = D tan θ2
S = D(tan θ1 – tan θ2)
D = S/(tan θ1 – tan θ2) ……..Eqn 10.13
And V = D tan θ2 = S tan θ2/(tan θ1 – tan θ2) …………Eqn. 10.14
R.L. Of staff station P = R.L. Of the line of sight + V – h.
Case II:
When both the observed angles are angles of depression:
S = QB – QA = D (tan θ2 – tan θ1)
D = S/(tan θ2 – tan θ1) ………….Eqn. 10.15
And V = D tan θ = S.tanθ2 /(tan θ2 – tan θ1 ) ……………..Eqn. 10.16
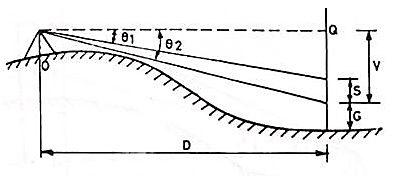
R.L. Of staff stn. P = R.L. Of the line of sight - V - h
Case III
When one of the observed angle is the angle of elevation and the other an angle of depression:
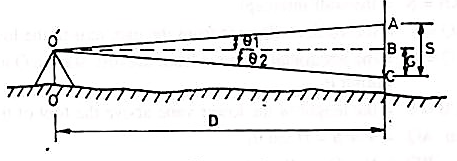
S = AC = AB + BC = D (tan θ1 + tan θ2)
D = S /(tan θ1 + tan θ2) …………Eqn. 10.17
And V = D tan θ2 = Stan θ2/(tan θ1 + tan θ2) ………..Eqn. 10.18
R.I. Of staff station = R.I. Of line of sight – V - h
Q9) What is sub tense bar measurements?
A10)
A subtense bar is a horizontal staff with targets fixed at a known distance apart. It is about 4m long having a small spirit level and a quick levelling head.
A sight rule, provided at its centre, can be placed along the line of sight by viewing the telescope of the theodolite thought the vanes. The bar is mounted on a tripod and is placed at right angles to the line of sight for making observations. After levelling and aligning, it is clamped by means of clamp screw.
The targets, made of discs of about 20 cm diameter are painted red on one side, and white on the other. The centres of body the sides of the targets are painted black in 7.5 cm diameter. The targets are placed at a distance of 2.5 m and 3 m. When the targets are placed 2.5 m apart, the white faces are to face the instrument and when they are placed 3m apart, the red faces face the instrument.
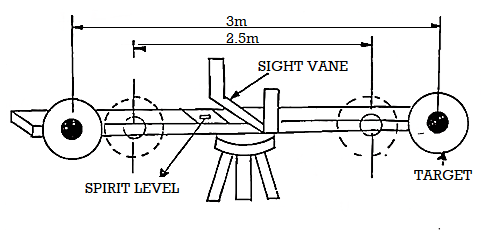
The horizontal and vertical angles are measured with a transit theodolite. For measuring vertical angles the method will be similarly to the movable hair method of stadia tacheometry and the distances are similarly deduced. For measuring horizontal angles, subtended at the instrument station by the two targets, the method of repetition is used, the horizontal distance.
D between the instrument station and the subtense bar station is found as follows:
Let O= the position of the instrument for measuring the horizontal angle 0 by the horizontal circle of theodolite.
AB= horizontal base of a length S.
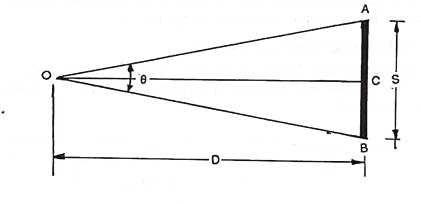
If line AB is perpendicular to OC, where C is midway between A and B, then from triangle OAC,
D = ½ S cot θ/2
Or D = S/(2 tan θ/2) ……..(i)
If θ is small, then
Tan θ/2 = θ/2, where θ is in raians
= ½ . θ/206265 if θ is in seconds.
(1 radian = 206265 seconds).
Putting this value in (i) above, we get
D = (S 206265)/θ ……..(ii)
Q10) Explain Levelling by Stadia
A11)
Levelling by stadia tachometry is an indirect and rapid method of levelling. It is suitable where country is rough and the precision needed is not great. The transit should preferably be provided with a sensitive control level for the vertical vernier so that the error may be readily eliminated.
The method of running a line of levels by this method is as follows:
(i) Set up the transit at a convenient point.
(ii) Take a back sight on the staff held at a B.M., first by observing the stadia interval and then by measuring the vertical angle to some arbitrarily chosen mark on the staff.
(iii) Establish a change point in advance of the transit, and take similar observations, the vertical angle being measured with horizontal cross-hari set on the same mark as before.
(iv) Move the trait to a new point in advance of the change point and repeat the process.
(v) Record the stadia distance and vertical angles and also the staff reading which is used as an index when vertical angles are measured.
The objectives, product of discs of approximately 20 cm diameter are painted crimson on one side, and white at the other.
The centers of frame the perimeters of the objectives are painted black in 7.five cm diameter. The objectives are positioned at a distance of 2.five m and three m. When the objectives are positioned 2.5 m apart, the white faces are to stand the tool and while they're positioned 3m apart, the crimson faces face the tool.
Sub tense Bar
The horizontal and vertical angles are measured with a transit theodolite. For measuring vertical angles the technique might be further to the movable hair technique of stadia tachometry and the distances are further deduced. For measuring horizontal angles, subtended on the tool station via way of means of the 2 objectives, the technique of repetition is used, the horizontal distance.
D among the tool station and the sub tense bar station is located as follows:
Let
O= the location of the tool for measuring the horizontal perspective zero via way of means of the horizontal circle of theodolite.
AB= horizontal base of a period S. Levelling via way of means of Stadia: Levelling via way of means of stadia tachometry is an oblique and fast technique of levelling.
It is appropriate wherein U. S. Is difficult and the precision wanted isn't always great.
The transit need to rather be supplied with a touchy manage degree for the vertical dernier in order that the mistake can be effortlessly eliminated. The technique of walking a line of degrees via way of means of this technique is as follows:
(i) Set up the transit at a handy factor.
(ii) Take a again sight at the personnel held at a B.M., first via way of means of watching the stadia c language after which via way of means of measuring the vertical perspective to a few arbitrarily selected mark at the personnel.
(iii) Establish an alternate factor earlier of the transit, and take comparable observations, the vertical perspective being measured with horizontal cross-hari set at the identical mark as before.
(iv) Move the trait to a brand new factor earlier of the alternate factor and repeat the process.
(v) Record the stadia distance and vertical angles and additionally the personnel studying that's used as an index while vertical angles are measured.
Q11) What are the errors in stadia surveying?
A12)
Errors and Precautions in Tachometric Surveying:
- The defects can be technical faults resulting from deception and seeing, or herbal causes.
- Imperfect everlasting modifications with inside the tool and wrong graduations at the stadia rod can cause the instrumental mistakes.
- Before beginning the research, whilst the tool is in complete everlasting adjustment, the constants of the tool furnished via way of means of the producer have to be showed via way of means of real remark with inside the area.
- It is specifically applicable for vital surveys in which the maximum sizeable parameter is precision (and now no longer the time).
- The graduations at the rod have to be carefully checked and vital changes have to be made to the measured measurements if a few distinction is found.
- The mistakes springing up from manipulation and recognizing depend upon the surveyor’s productiveness and abilities.
- Which are prompted via way of means of insufficient tool centering and lowering, and faulty readings of the Stadia? There have to be no Parallax to certainly see the stadia pin.
- When taking stadia hair readings, warning may be taken to look if the axial hair isn't pressured for stadia hair.
- The precision of stadia hair readings may be examined via way of means of seeing if the imply of stadia hair readings is equal to axial hair reading.
- Wind, unequal enlargement of the tool components, and visibility and unequal refraction can purpose mistakes because of herbal causes.
- The maximum vital of those is the second.
- This is attributed to the differential refraction of mild rays via way of means of transferring through numerous strain layers of soil.
- Therefore, so one can save you this mistake, noon readings could be stopped to the diploma practicable.
- The most allowable hole with inside the distance is 1 in 500 to at least one in 900 and in elevations 0.08 to 0.10 m.
- Always, the sightlines want now no longer be beneath a meter from the level.
- The final blunders in a traverse of the tachometry does now no longer surpass 0. LIFE, in which p is the meter diameter of the traverse.
Unit - 1
Tachometric Surveying
Q1) What is tachometric surveying?
A1)
Tachometric surveying is a technique of angular surveying wherein the horizontal distance from the device to the group of workers stations are decided from instrumental observations only.
Thus the chaining operations are eliminated. Field Work may be finished very swiftly Tachometry is specifically used for making ready the contour plans of regions.
As chaining is avoided, as a ways as possible, this technique of surveying is excellent proper in damaged and hilly regions, regions protected with stretches of water, Swamps, etc. wherein chaining becomes very slow, tedious and inaccurate.
Tachometric surveying is a technique of angular surveying wherein the horizontal distance from the
A tachometer is much like an everyday transit theodolite geared up with stadia wires similarly to the imperative cross-hairs.
As accuracy and velocity are necessary, the telescope geared up with a tachometer need to satisfy extra requirements. Also, the vertical circle have to be greater refined.
The telescope of the tachometer is commonly longer than that of the Ordinary theodolite and has a better strength of magnification. The item glass is of extra diameter, and the lens machine is of higher quality. The magnification strength have to now no longer be much less than 20-25.
This precept is utilized in special techniques in special ways.
Mainly there are techniques of tachometry survey.
(1) Stadia machine, and
(2) Tangential machine.
Q2) What are the methods of tachometric surveying?
A2)
1. Stadia System of Tachometry:
In the stadia machine, the horizontal distance to the team of workers Station from the tool station and the elevation of the team of workers station regarding the road of sight of the tool is received with best one commentary from the tool Station. In the stadia technique, there are specially structures of surveying.
(1) Constant hair technique and,
(2) Movable hair technique.
i. Fixed Hair Method:
In the constant hair technique of tachometric surveying, the tool hired for taking observations encompass a telescope geared up with extra horizontal go hairs one above and the alternative underneath the critical hair.
These are located equidistant from the critical hair and are known as stadia hairs.
When a team of workers is considered via the telescope, the stadia hairs are visible to intercept a sure period of the team of workers, and this varies immediately with the space among the tool and the stations.
As the space among the stadia hair is constant, this technique is known as the “constant hair technique.”
Ii. Movable Hair Method;
In the movable Hair technique of tachometric surveying, the tool used for taking observations encompass a telescope geared up with stadia hairs which may be moved and stuck at any distance from the critical hair (in the limits of the diaphragm).
The team of workers used with this tool includes objectives (marks) at a set distance apart (say 3.four mm).
The Stadia c language that's variable for the special positions of the team of workers is measured, and the horizontal distance from the tool station to the team of workers station is computed.
2. Tangential System of Tachometric Surveying:
In this machine of tachometric surveying, observations might be important from the tool station to the team of workers station to decide the horizontal distance and the distinction with inside the elevation among the road of collimation and the team of workers station.
The best gain of this technique is this survey may be carried out with everyday transit theodolite.
As the everyday transit theodolite are inexpensive than the difficult and greater delicate tachometer, so, the survey might be greater economical.
So, as some distance the discount of discipline notes, distances and elevations are worried there isn't plenty distinction among those structures.
But this machine is taken into consideration not as good as the stadia machine because of the subsequent motives and may be very seldom used nowadays.
This entails size of vertical angles, and the tool might also additionally get disturbed among the 2 observations.
The pace is decreased because of greater range of observations and the adjustments with inside the atmospheric situations will have an effect on the readings considerably.
The team of workers used on this technique is much like the only hired with inside the movable hair technique of stadia surveying. The distance among the objectives or vanes can be 3-4 m.
Q3) Explain principal of stadia method
A3)
Spaced both aspect of it. These stadia traces outline the constant parallaxes attitude.
If the theodolite telescope is sighted directly to a levelling personnel and the readings of the outer traces noted, the distinction with inside the readings, the personnel intercept (s), may be immediately proportional to the horizontal distance among the device and the personnel.
Generally, the gap among the stadia traces is designed in this type of way that the horizontal distance Z>H among the device and personnel is given through: wherein Z) s= slope distance, and 0=vertical attitude measured through the theodolite.
Therefore: wherein swabs = distinction in peak among A and B, h, = peak of device (trunnion axis to ground), m = center hair studying, and V= distinction in peak among center-hair studying and grunion axis = 50s sin 20 (6. 11)
Several self-decreasing tachometers have additionally been designed.
The major gain of those gadgets is their capacity to make amends for the impact of the inclination of the theodolite telescope and, hence, permit the direct willpower of horizontal distance without extra computation.
Two outstanding examples of this form of device are the Wild RDS vertical personnel self-decreasing tachometer and the Kern DK-RT horizontal bar double-photograph self-decreasing tachometer.
Details of the development and use of those gadgets can be observed in Hodges and Greenwood, five and Smith.6 In latest years, the manufacture of those particular optical gadgets has ceased, their location being taken through low-price digital measuring gadgets.
Q4) What is sub tense bar?
A4)
The 2d approach (constant base, variable attitude) is normally called the sub tense or horizontal sub tense bar technique.
The technique is generally restricted to the size of distance for manage purposes. Using this approach, distances can be decided with a proportional blunders of as much as 1/10000. The instrumentation required includes a sub tense bar, generally 2 m long, and a one-2d theodolite, consisting of the Wild T2.
The bar has goals established at every give up of an invar strip. The strip is covered through a surrounding aluminum strip which will make sure that, for all sensible purposes, the duration of the bar stays consistent at 2 m.
The bar is installation and orientated at proper angles to the road of sight of the theodolite
Tachometry is a department of surveying wherein the horizontal and vertical distances are decided via way of means of angular observations with a tachometer, the chaining operation being altogether removed
Tachometry isn't as correct as is changing, however it's far a long way extra fast in tough and tough use wherein levelling is tedious and chaining is each misguided and slow.
Thus it's far high-quality proper whilst boundaries together with steep and damaged ground, deep ravines, stretches of water or swamps are met with Tachometry is specially used even as getting ready contour plans and traversing and is likewise appropriate for hydrographic surveys, vicinity surveys of roads, railways, etc.
It is likewise once in a while hired for small surveys wherein elevations aren't decided.
Q5) Explain theory of analytic lens
A5)
Analytic lens is a further lens used with inside the device. It is a unique lens that's located among the item glass and the eyepiece of the telescope on the way to put off the additive consistent (f+d).
This is executed to make the expression for the space among device station and workforce role extra simplified.
Tachometry is a department of angular surveying wherein the horizontal and vertical distances of factors are received with the aid of using instrumental observation. The device normally hired in tachometry is a tachometer and a levelling workforce.
A tachometer in a popular sense, is a transit Theodolite having a stadia telescope i.e. a telescope equipped with a stadia diaphragm, i.e. a telescope prepared with horizontal hairs referred to as stadia hairs further to the everyday cross- hairs.
The values of f/i and (f+d) are normally marked on a card connected to the interior of field with the aid of using the maker.
Multiplying consistent price is normally one hundred and additive consistent (f+d) price various from 30 to 60 cm with inside the case of an outside focusing telescope and with inside the case of an inner focusing telescope it varies from eight to twenty cm.
The item of presenting a further convex lens, referred to as an analytic lens, with inside the telescope is to put off the additive consistent (f+d). That means (f+d) might be zero.
Stadia metric range finding, or the stadia approach, is a way of measuring distances with a telescopic instrument.
The time period stadia comes from a Greek unit of period Station (identical to six hundred Greek toes, opus) which became the everyday period of a sports activities stadium of the time.
Stadia metric range finding is used for surveying and with inside the telescopic points of interest of firearms, artillery pieces, or tank guns, in addition to a few binoculars and different optics.
It remains extensively utilized in long-variety army sniping, however in lots of expert programs it's far being changed with microwave, infrared, or laser range finding methods.
Although a whole lot simpler to use, digital rangefinders can supply away the shooter's role to a well-geared up adversary, and the want for correct variety estimation existed for a whole lot longer than digital rangefinders small and rugged sufficient to be appropriate for army use.
The stadia approach is primarily based totally upon the precept of comparable triangles. This way that, for a triangle with a given attitude, the ratio of contrary facet period to adjoining facet period (tangent) is constant.
By the use of a reticle with marks of an acknowledged angular spacing, the precept of comparable triangles may be used to locate both the gap to gadgets of acknowledged length and the dimensions of gadgets at an acknowledged distance.
In both case, the acknowledged parameter is used, together with the angular measurement, to derive the period of the alternative facet.
Since a radian is described because the attitude fashioned while the period of a round arc equals the radius of the circle, a mill radian is the attitude fashioned while the period of a round arc equals 1/a thousand of the radius of the circle.
For telescopic angles, the approximations of substantially simplify the trigonometry, permitting one to scale gadgets measured in mill radians through a telescope through an element of a thousand for distance or height.
An item five meters excessive, for example, will cowl 1 mad at 5000 meters, or five mad at a thousand meters, or 25 mad at 2 hundred meters.
Since the radian expresses a ratio, it's far impartial of the gadgets used; an item 6 toes excessive overlaying 1 mad could be 6000 toes distant. In practice, it is able to be visible that tough approximations can be made with a proper triangle whose base (b) is identical to the gap of the 'rangefinder' from the eye; with the aperture (a) being the hollow through which the goal is sighted – the apex of this triangle being at the floor of the user's eye.
Q6) Explain various terms used in tachometric surveying?
A6)
Height and Distance
It is an important application of trigonometry which helps us to find the height of any object and distance of that object from any point which are not directly measurable. If the angle of elevation/depression from a point is known.
Line of Sight
A line of sight is the line drawn from the eye of an observer to the point, where the object is viewed by the observer.
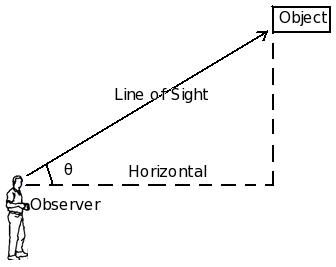
Fig. Angle of elevation
In this diagram, marks the angle of elevation of the top of the object as seen from a point on the ground.
Horizontal Line
The line of sight which is parallel to ground level is known as horizontal line.
Angle of Elevation
The angle of elevation of the point viewed is the angle formed by the line of sight with the horizontal, when the point being viewed is above the horizontal level.
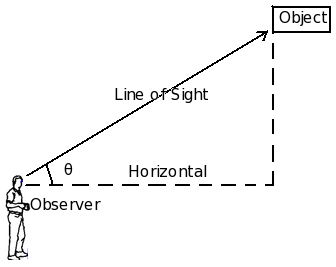
Fig. Angle of elevation
As shown in the diagram above, an observer is looking at an object located above the horizontal axis. In this process, it makes an angle with the x-axis. This angle is called angle of elevation.
Understanding the angle of elevation formula:
The angle of elevation formula helps to solve the angle of elevation problems very easily. As it is visible from the figure, the vertical from object makes a right angle with the horizontal. So if we know the height of the object and the linear distance, we can easily find out the angle by trigonometric formula. It is given by tan = Height / distance. The angle of elevation of the sun that is better known as altitude angle, can also be found by the same method.
Angle of Depression
When the line of sight is below the horizontal level, the angle so formed by the line of sight with the horizontal is called the angle of depression.
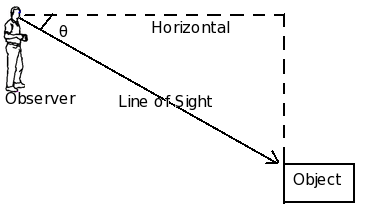
Fig. Angle of depression θ
As shown, an observer is looking at the downwards object while making an angle with the horizontal axis. Here θ can be called the angles of depression for an observer.
Height and Distance: One of the main application of trigonometry is to find the distance between two or more than two places or to find the height of the object or the angle subtended by any object at a given point without actually measuring the distance or heights or angles. Trigonometry is useful to astronomers, navigators, architects and surveyors etc. in solving problems related to heights and distances.
Height and Distance
The directions of the objects can be described by measuring:
- Angle of elevation
- Angle of depression
Angles of elevation or angles of depression of the objects are measured by an instrument called Theodolite. Theodolite is based on the principles of trigonometry, which is used for measuring angles with a rotating telescope. In 1856, Sir George Everest first used the giant theodolite, which is now on display in the Museum of the survey of India in Dehradun
Angle of Elevation
Let P be the position of the object above the horizontal line OA and O be the eye of the observer, then angle AOP is called angle of elevation. It is called the angle of elevation, because the observer has to elevate (raise) his line of sight from the horizontal OA to see the object P. [When the eye turns upwards above the horizontal line].

Line of sight: It is the line drawn from the eye of an observer to the object viewed.
Q7) What is angle of depression?
A7)
Angle of Depression
Let P be the position of the object below the horizontal line OA and O be the eye of the observer, then angle AOP is called angle of depression.
It is called the angle of depression because the observer has to depress (lower) his line of sight from the horizontal OA to see the object P.
Below the eye level: If the object lies below the horizontal plane of our eyes, then we have to move our head downwards to view it. In doing so, our lines of sight moves downwards through an angle and the angle, which the line of sight now makes with the horizontal line, is called the angle of depression of the object from our eyes.
Example : Let OH be the horizontal line at the eye level. If a person at O looks at an object P lying below the eye level, then, ∠HOP is the angle of depression of P as seen from O.
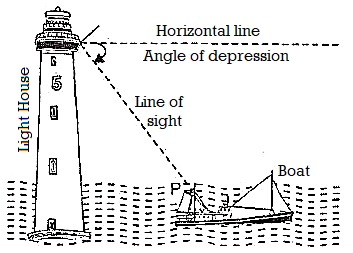
Note: Angle of depression of P as seen from O = angle of elevation of O, as seen from P.
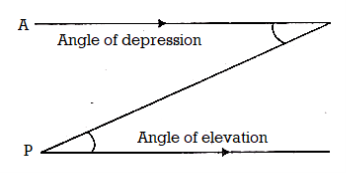
∴∠AOP = ∠OPH
Height and Distance Important Points
- In solving problems observer is represented by a point if his height is not given.
- In solving problems object is represented by a line segment and some times by a point if height or length is not considered.
For example, AB is tower and point C is observer.
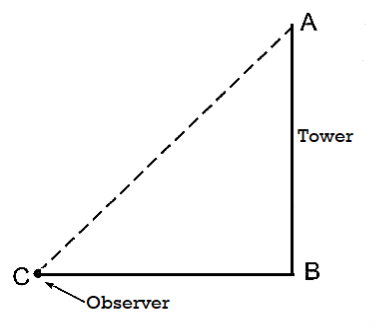
- A line drawn parallel to earth surface is called horizontal line.
- The angle of elevation and depression are always acute angles.
- If the observer moves towards the objects like tower, building, cliff, etc. then angle of elevation increases and if the observer moves away from the object, the angle of elevation decreases.
- If the angle of elevation of sun decreases, then the length of shadow of an object increases and vice-versa.
- If in problems, the angle of elevation of an object is given, then we conclude that the object is at higher altitude than observer. The angle of depression implies that observer is at higher altitude than object.
Q8) Explain Height and Distance Questions
A8)
1. If a pole 6 m high casts a shadow 2√3 m long on the ground, find the Sun’s elevation.
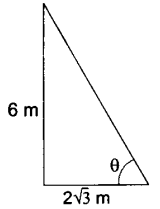
Tan θ = 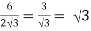
θ = 60o
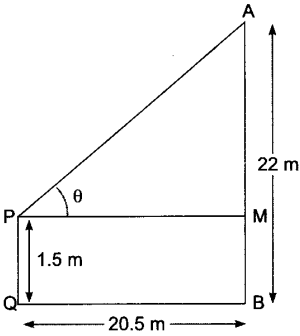
2. An observer 1.5 m tall is 20.5 m away from a tower 22 m high. Determine the angle of elevation of the top of the tower from the eye of the observer.
PQ = MQ = 1.5 m
AM = AB – MB = 22 – 1.5 = 20.5 m
Now in APM
Tan θ = AM/PM
= 20.5/20.5 = 1
= 45o
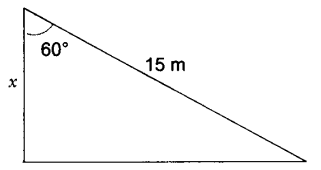
3. A ladder 15 m long makes an angle of 60o with the wall. Find the height of the point where the ladder touches the wall.
Cos 60o = x/15
½ = x/15 x = 15/2 m = 7.5 m
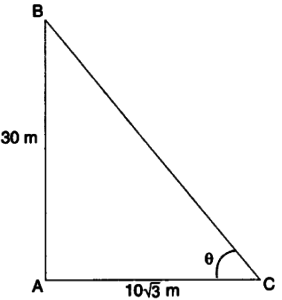
4. The ratio of the height of a tower and the length of its shadow on the ground is √3 : 1. What is the angle of elevation of the sun?
Given: AB/BC = 3/1
Then, tan θ = AB/BC = 3
θ = 60o
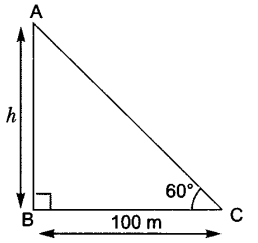
5. If the angle of elevation of a tower from a distance of 100 m from its foot is 60°, then what will be the height of the tower?
Let h be the height of the tower.
Tan 60o = AB/BC
3 = h/100
h = 103 m.

6. In Fig., AB is a 6 m high pole and CD is a ladder inclined at an angle of 60° to the horizontal and reaches up to a point D of pole. If AD = 2.54 m, find the length of the ladder, (use √3 =1.73)
DB = (6 – 2.54)m = 3.46 m
In BDC, sin 60o = BD/CD
3/2 = 3.46/CD CD = (3.46 2)/1.73
DC = 4 m
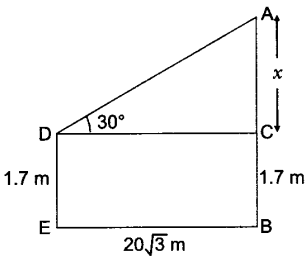
7. An observer, 1.7 m tall, is 20 √3 m away from a tower. The angle of elevation from the eye of observer to the top of tower is 30°. Find the height of tower.
Let AB be the height of tower and DE be the height of observer.
Then in ACD, AC/DC = tan 30o
x/203 = tan 30o = 1/3 x = 20 m
AB = 20 + 1.7 = 21.7 m
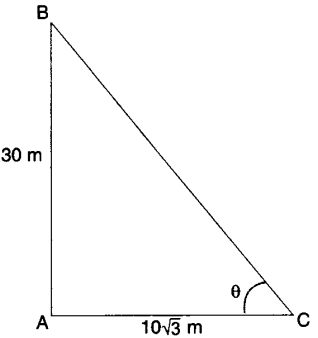
8. If a tower 30 m high, casts a shadow 10 √3 m long on the ground, then what is the angle of elevation of the sun?
In ABC
Tan θ = AB/AC = 30/103 = 3
tan θ = tan 60
θ = 60o
Q8) Explain tangential method
A9)
The Tangential System of Tachometry:
This method is used when the telescope is not fitted with a stadia diagram. In this method, the telescope is directed towards the staff to which the horizontal and vertical distances are to be measured and two vertical angles to two vanes or targets on the staff at a known distance (S) apart are taken.
The horizontal and vertical distances are then calculated as follows:
Case 1:
When both the observed angles are angles of elevation:
O=the instruments station.
O’=the position of the instruments axis
P= the staff station.
∠AO’Q= θ1= vertical angle to the upper vane.
∠BO’Q= θ2 =” “ “ lower
AB=S=the staff intercept.
BQ=V= the horizontal distance from the inst, axis to the lower vane.
O’Q=D= the horizontal distance from the inst. Station O to the staff station P
PB= h= the height of the lower vane above the foot of the staff.
BQ = V = D tan θ2
S = D(tan θ1 – tan θ2)
D = S/(tan θ1 – tan θ2) ……..Eqn 10.13
And V = D tan θ2 = S tan θ2/(tan θ1 – tan θ2) …………Eqn. 10.14
R.L. Of staff station P = R.L. Of the line of sight + V – h.
Case II:
When both the observed angles are angles of depression:
S = QB – QA = D (tan θ2 – tan θ1)
D = S/(tan θ2 – tan θ1) ………….Eqn. 10.15
And V = D tan θ = S.tanθ2 /(tan θ2 – tan θ1 ) ……………..Eqn. 10.16
R.L. Of staff stn. P = R.L. Of the line of sight - V - h
Case III
When one of the observed angle is the angle of elevation and the other an angle of depression:

S = AC = AB + BC = D (tan θ1 + tan θ2)
D = S /(tan θ1 + tan θ2) …………Eqn. 10.17
And V = D tan θ2 = Stan θ2/(tan θ1 + tan θ2) ………..Eqn. 10.18
R.I. Of staff station = R.I. Of line of sight – V - h
Q9) What is sub tense bar measurements?
A10)
A subtense bar is a horizontal staff with targets fixed at a known distance apart. It is about 4m long having a small spirit level and a quick levelling head.
A sight rule, provided at its centre, can be placed along the line of sight by viewing the telescope of the theodolite thought the vanes. The bar is mounted on a tripod and is placed at right angles to the line of sight for making observations. After levelling and aligning, it is clamped by means of clamp screw.
The targets, made of discs of about 20 cm diameter are painted red on one side, and white on the other. The centres of body the sides of the targets are painted black in 7.5 cm diameter. The targets are placed at a distance of 2.5 m and 3 m. When the targets are placed 2.5 m apart, the white faces are to face the instrument and when they are placed 3m apart, the red faces face the instrument.
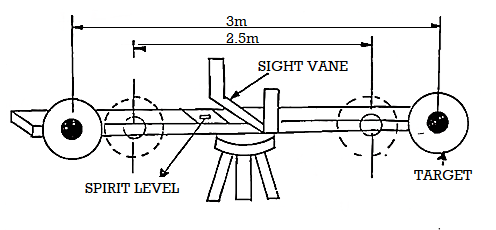
The horizontal and vertical angles are measured with a transit theodolite. For measuring vertical angles the method will be similarly to the movable hair method of stadia tacheometry and the distances are similarly deduced. For measuring horizontal angles, subtended at the instrument station by the two targets, the method of repetition is used, the horizontal distance.
D between the instrument station and the subtense bar station is found as follows:
Let O= the position of the instrument for measuring the horizontal angle 0 by the horizontal circle of theodolite.
AB= horizontal base of a length S.
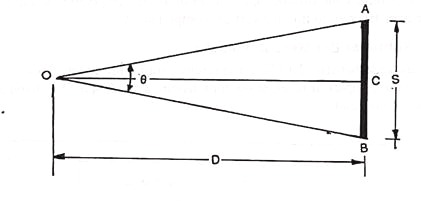
If line AB is perpendicular to OC, where C is midway between A and B, then from triangle OAC,
D = ½ S cot θ/2
Or D = S/(2 tan θ/2) ……..(i)
If θ is small, then
Tan θ/2 = θ/2, where θ is in raians
= ½ . θ/206265 if θ is in seconds.
(1 radian = 206265 seconds).
Putting this value in (i) above, we get
D = (S 206265)/θ ……..(ii)
Q10) Explain Levelling by Stadia
A11)
Levelling by stadia tachometry is an indirect and rapid method of levelling. It is suitable where country is rough and the precision needed is not great. The transit should preferably be provided with a sensitive control level for the vertical vernier so that the error may be readily eliminated.
The method of running a line of levels by this method is as follows:
(i) Set up the transit at a convenient point.
(ii) Take a back sight on the staff held at a B.M., first by observing the stadia interval and then by measuring the vertical angle to some arbitrarily chosen mark on the staff.
(iii) Establish a change point in advance of the transit, and take similar observations, the vertical angle being measured with horizontal cross-hari set on the same mark as before.
(iv) Move the trait to a new point in advance of the change point and repeat the process.
(v) Record the stadia distance and vertical angles and also the staff reading which is used as an index when vertical angles are measured.
The objectives, product of discs of approximately 20 cm diameter are painted crimson on one side, and white at the other.
The centers of frame the perimeters of the objectives are painted black in 7.five cm diameter. The objectives are positioned at a distance of 2.five m and three m. When the objectives are positioned 2.5 m apart, the white faces are to stand the tool and while they're positioned 3m apart, the crimson faces face the tool.
Sub tense Bar
The horizontal and vertical angles are measured with a transit theodolite. For measuring vertical angles the technique might be further to the movable hair technique of stadia tachometry and the distances are further deduced. For measuring horizontal angles, subtended on the tool station via way of means of the 2 objectives, the technique of repetition is used, the horizontal distance.
D among the tool station and the sub tense bar station is located as follows:
Let
O= the location of the tool for measuring the horizontal perspective zero via way of means of the horizontal circle of theodolite.
AB= horizontal base of a period S. Levelling via way of means of Stadia: Levelling via way of means of stadia tachometry is an oblique and fast technique of levelling.
It is appropriate wherein U. S. Is difficult and the precision wanted isn't always great.
The transit need to rather be supplied with a touchy manage degree for the vertical dernier in order that the mistake can be effortlessly eliminated. The technique of walking a line of degrees via way of means of this technique is as follows:
(i) Set up the transit at a handy factor.
(ii) Take a again sight at the personnel held at a B.M., first via way of means of watching the stadia c language after which via way of means of measuring the vertical perspective to a few arbitrarily selected mark at the personnel.
(iii) Establish an alternate factor earlier of the transit, and take comparable observations, the vertical perspective being measured with horizontal cross-hari set at the identical mark as before.
(iv) Move the trait to a brand new factor earlier of the alternate factor and repeat the process.
(v) Record the stadia distance and vertical angles and additionally the personnel studying that's used as an index while vertical angles are measured.
Q11) What are the errors in stadia surveying?
A12)
Errors and Precautions in Tachometric Surveying:
- The defects can be technical faults resulting from deception and seeing, or herbal causes.
- Imperfect everlasting modifications with inside the tool and wrong graduations at the stadia rod can cause the instrumental mistakes.
- Before beginning the research, whilst the tool is in complete everlasting adjustment, the constants of the tool furnished via way of means of the producer have to be showed via way of means of real remark with inside the area.
- It is specifically applicable for vital surveys in which the maximum sizeable parameter is precision (and now no longer the time).
- The graduations at the rod have to be carefully checked and vital changes have to be made to the measured measurements if a few distinction is found.
- The mistakes springing up from manipulation and recognizing depend upon the surveyor’s productiveness and abilities.
- Which are prompted via way of means of insufficient tool centering and lowering, and faulty readings of the Stadia? There have to be no Parallax to certainly see the stadia pin.
- When taking stadia hair readings, warning may be taken to look if the axial hair isn't pressured for stadia hair.
- The precision of stadia hair readings may be examined via way of means of seeing if the imply of stadia hair readings is equal to axial hair reading.
- Wind, unequal enlargement of the tool components, and visibility and unequal refraction can purpose mistakes because of herbal causes.
- The maximum vital of those is the second.
- This is attributed to the differential refraction of mild rays via way of means of transferring through numerous strain layers of soil.
- Therefore, so one can save you this mistake, noon readings could be stopped to the diploma practicable.
- The most allowable hole with inside the distance is 1 in 500 to at least one in 900 and in elevations 0.08 to 0.10 m.
- Always, the sightlines want now no longer be beneath a meter from the level.
- The final blunders in a traverse of the tachometry does now no longer surpass 0. LIFE, in which p is the meter diameter of the traverse.