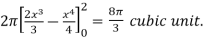Unit - 2

Integral calculus-II

Q1) What do you understand by tracing of curves?

A1)

A picture explains more clearly than words and numbers. A curve which is the image of functional relationship gives us a lot information about the relation. We can get information analyzing the equation itself but the associated curve is often easy and understandable.

Let’s study about how to trace the curves of various equations in different forms like Cartesian, parametric and polar.

Important definitions for curve tracing

Here are some terms that we use in curve tracing:

1. Double point- when a curve passes two times through this point is known as double point.

2. Node- a double point at which two real tangents can be drawn.(tangents should not be coincide)

3. Cusp -  a double point is a cusp when two tangents are coincide on it.

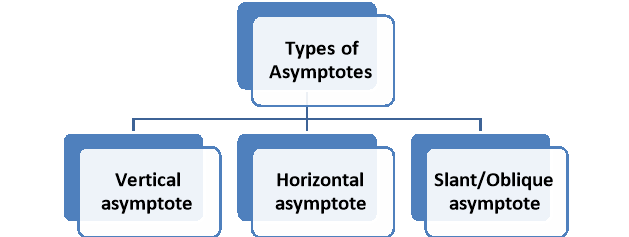
Q2) What are asymptotes?

A2)

An asymptote of a curve of function y = f(x) is a line which does not intersect on the graph.

Types of asymptotes-

Q3) Determine the vertical asymptote of the function-

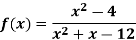
A3)

Here we have-

We can write the given function as-

We can notice here as x gets closer to 3 from the left, then the value of the function gets smaller, approaching -∞ and x gets closer 3 from the right, then the value of the function gets larger and approaches +∞.

So that x = 3 is a vertical asymptote same as x = -4 is another vertical asymptote.

Q4) Find the horizontal asymptote of the function-

A4)

Find the limits-

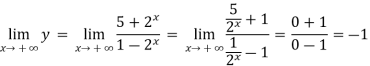
And

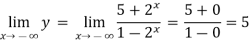
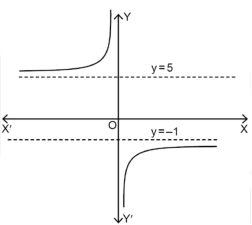
Hence the horizontal asymptotes are y = -1 and y = 5.

Figure will be as follows of the asymptotes of the given function-

Q5) Find the slant asymptotes of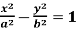 

A5)

We have,

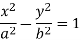
Which can be written as-

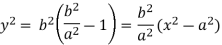
The value of ‘m’ will be-

=     = 

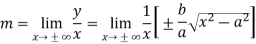
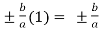
Now we can find ‘c’ as –

c = = =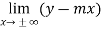

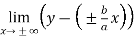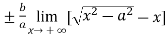
= 0

Hence the slant asymptotes are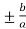

Q6) Find the slant asymptote of the function f(x) = x + .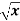

A6)

Find the value of m-

Hence the y = x + c,

Now find c-

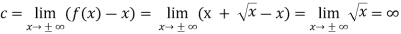
Here c must not be infinite.

So we can say that f does not have a slant asymptote at ∞.

Q7) Trace the curve y = 1/x².

A7)

As we can see y- coordinates of the curve can not be negative. So the                                              curve must be above x-axis. The curve is also symmetric about y-axis so we can draw the graph only in single side.

Here, we will find the first and second derivatives-

So, dy/dx= -2/x³ and d²y/dx² = 6/ x⁴    ,  here  dy/dx <0 for all x>0 so we can say that the function is non- increasing so the graph falls as we increase x.

Also second derivative is also non zero so there are no point of inflection.

Here the curve is x²y=1 (rewritten), here both the axes are asymptotes of the curve.

Here is the figure of the curve-:

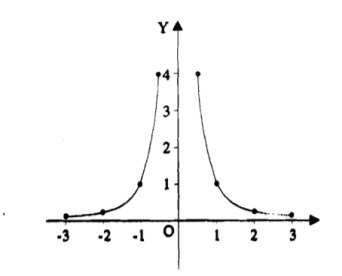
Q8) Trace the curve of the following parametric equations:

x(t) = t-1,     y(t) = 2t+4         -3<

A8)

Here we will create the table for t, x(t) and y(t), t is independent variable in both case,

Here value of t lies between -3 to 2.

By plotting these set of point we get a curve as below.

Arrows in the graph indicates the orientation of the graph.

Q9) How do we trace a curve in polar form?

A9)

Tracing a curve- polar form

To trace the polar curve r = f ( we follow the following steps:

1. Symmetry – (a) if the equation is an even function of 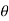, then the curve is symmetrical about the initial line.

(b) if the equation is an even function of r, then the curve is symmetrical about the origin/

(C ). If the equation remains same if we change 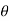by -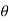 and r by –r then the curve is symmetric about the line through the pole and perpendicular to the initial line.

2. Region- Find the reason for 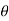for which r is defined and real

3. Table- make table for the values of r determined by .

4. Angle 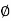-  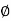is the angle between the radius vector and tangent to the curve;

= )

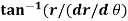Then angle 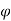= 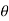+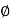, tangents to the curve can be determined by angle

5. Asymptotes-   find the asymptotes of the curve.

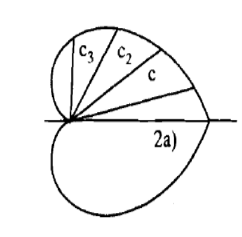
Q10) Trace the curve r = a(1+ cos.

A10)

Here we can see clearly cos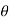 = cos(-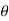), hence the curve is symmetric about initial line.

Since -1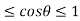, the curve lies inside the circle r = 2a

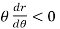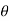= -asin , when  0, thus r decreases as increases in the interval 0 to

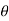	0
r	2a	A	0

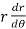= - cot (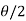) = tan(+ ),      this shows the angle between r and and the tangent is 0 or according to   0 or . Hence the line joining a point on the curve to the origin is orthogonal to the tangent when = 0 and coincides with

From the above results, we can easily draw the graph above the initial line

Q11) find the area under the curves where f(x) =  x+4 and g(x) =  3 – x/2 over the interval [1,4]

A11)

Here limits are given a = 1 , b = 4,

We know that, area under the curve,

A =

= 

=

= 

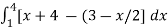
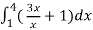
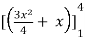
=  (16 – 7/4) =  57/4

So that the area of the region is 57/4 unit square.

Q12) Find the area under the curves where y =  x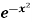 and y =  x + 1,         x = 2 and y-axis.

A12)

When we draw the graph, curve does not meet, but depend on two vertical lines,

Here boundary is [0 , 2]

Area under the curve,

A =

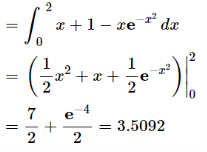
So that the area under the curve is 3.2092 unit square.

Q13) Define average function value with an example.

A13)

We can use definite integrals to find out the average value of a function.

The average value of a function over the interval [a , b]  is given by the following expression ,

f( avg.) =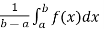

For example: find the average value of the function f(x) = x³ over the interval[0,1].

Sol.  We know that

f( avg.) =

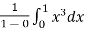=      =       = 1 / 4

Q14) Find the work done on a spring when we compress it from its natural length of 1m to the 0.75m, if the spring constant k = 16 N / m.

A14)

The force is given by,

F =16x

Here we start to compress it at x = 0 and finish at x= 0.25 from its natural length.

So we take lower limit and upper limit 0 and 0.25 respectively.

We know that,

W =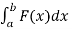

=

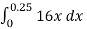
= 0.5 N.m

Q15) Let f(x) = 2 x³/², then calculate the arc length of the graph over interval [0,1].

A15) Here we can find its first derivative

f’(x) = 3 x¹/²

Such that,    

[f’(x)]² = 9x

Then we know that,

Length of Arc  =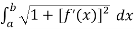

=

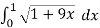
Now,

Let u = 1 + 9x , then du =  9 dx , when x = 0 then u = 1 and x = 1 then u = 10,

So,

=

=

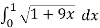
= 1/9 ×2/3 × =  2.268 units

Q16) Find the length of f(x) = x between x = 2 and x = 3.

A16)

The derivative of f(x) will be,

f’(x) = 1

And we know that,

Length of Arc  =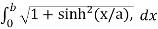

So that,

Length of Arc  =

=   

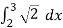
On solving the integral, we get

=  (3 – 2) = .

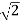Q17) Find the area lying inside the cardioid r = a(1+cosθ) and outside the circle r = a, by using double integration.

A17)

We have,

r = a(1+cosθ)   …………………….(1)

And

r = a ……………………………….(2)

On solving these equations by eliminating r , we get

a(1+cosθ)    =   a

(1+cosθ) = 1

Cosθ = 0

Here a θ varies from – π/2  to    π/2 

Limit of r will be a and 1+cosθ)   

Which is the required area.

Q18) Calculate the volume under the surface z = 3 + x² - 2y over the region R defined as 0≤ x ≤ 1 and  -x ≤ y ≤ x

A18)

The is a double integral of  z = 3 + x² - 2y over the region R .

Volume will be,

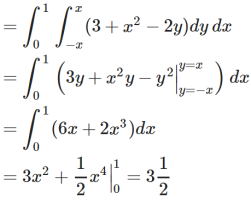
Q19) Find the volume of the solid of revolution formed by revolving R around y-axis of the function f(x) = 1/x over the interval [1 , 3].

A19)

The graph of the function f(x) = 1/x will look like-

The volume of the solid of revolution generated by revolving R(violet region) about the y-axis over the interval [1 , 3]

Then the volume of the solid will be-

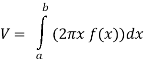
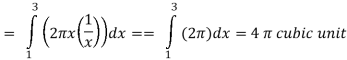
Q20) Find the volume of the solid of revolution formed by revolving R around y-axis of the function f(x) = 2x - x² over the interval [0 , 2].

A20)

The graph of the function f(x) = 2x - x² will be-

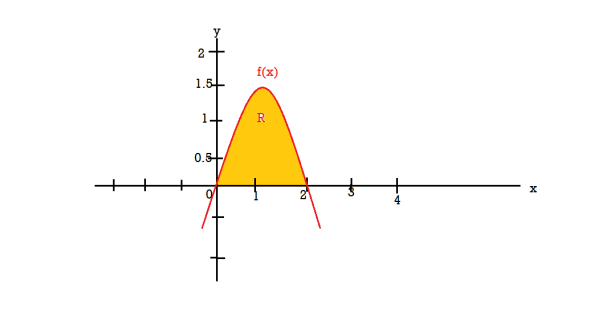
The volume of the solid is given by-

=
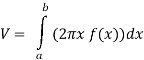
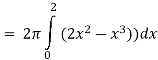