Unit - 5
Vector integral calculus
Q1) What do you understand by line integral?
A1)
The Line Integral- Let- F be vector function defined throughout some region of space and let C be any curve in that region. ṝis the position vector of a point p (x,y,z) on C then the integral ƪ F .dṝ is called the line integral of F taken over
Now, since ṝ =xi+yi+zk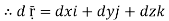
And if F͞ =F1i + F2 j+ F3 K
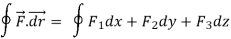
Q2) Evaluate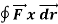 
where 
= (2xy +z2) I +x2j +3xz2 k along the curve x=t, y=t2, z= t3 from (0,0,0) to (1,1,1).
A2)
F x dr = 
Put x=t, y=t2, z= t3
Dx=dt ,dy=2tdt, dz=3t2dt.
F x dr =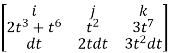 
=(3t4-6t8) dti – ( 6t5+3t8 -3t7) dt j +( 4t4+2t7-t2)dt k
=
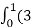t4-6t3)dti –(6t5+3t8-3t7)dt j+(4t4 + 2t7 – t2)dt k
=
=
+
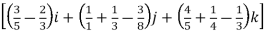
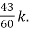
Q3) Evaluat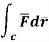e 
where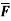 
=yz i+zx j+xy k and C is the position of the curve.
= (a cost)i+(b sint)j+ct k , from y=0 to t=π/4.
A3)
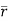= (a cost)i+(b sint)j+ct k
The parametric eqn. Of the curve are x= a cost, y=b sint, z=ct (i)
=
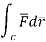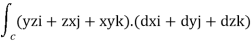
Putting values of x,y,z from (i),
Dx=-a sint
Dy=b cost
Dz=c dt
=
=
=
= 
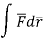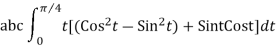
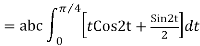
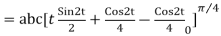
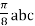
Q4) What is volume integral?
A4)
The volume integral is denoted by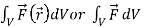 
And defined as-
If 
, then
Note-
If in a conservative field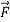 
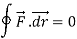
Then this is the condition for independence of path.
Q5) Evaluate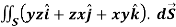 
, where S is the surface of the sphere 
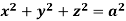in the first octant.
A5)
Here-
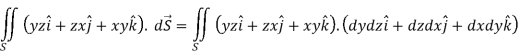
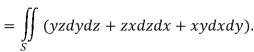
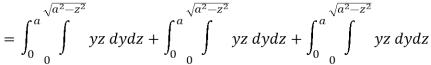
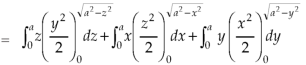
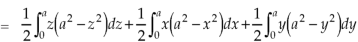
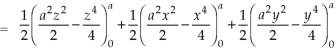
Which becomes-
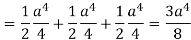
Q6) Evaluate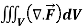 
if V is the region in the first octant bounded by 
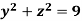and the plane x = 2 and 
.
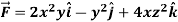A6)
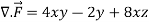
x varies from 0 to 2
The volume will be-
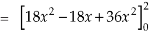
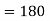
Q7) Verify stroke’s theorem when 
and surface S is the part of sphere 
, above the xy-plane.
A7)
We know that by stroke’s theorem,
Here C is the unit circle- 
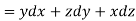
So that-
Now again on the unit circle C, z = 0
Dz = 0
Suppose,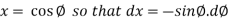 
And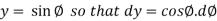 
Now
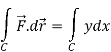
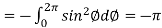……………… (1)
Now-
Curl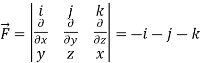 
Using spherical polar coordinates-
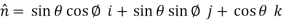
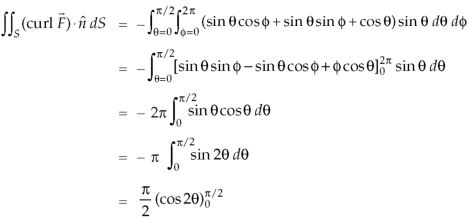
………………… (2)
From equation (1) and (2), stroke’s theorem is verified.
Q8) Verify Stoke’s theorem for the given function-
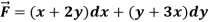
Where C is the unit circle in the xy-plane.
A8)
Suppose-
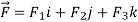
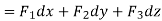
Here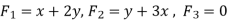 
We know that unit circle in xy-plane-
Or
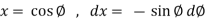
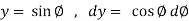
So that,
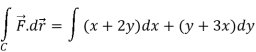
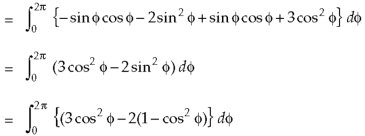
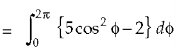
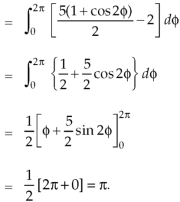
Now
Curl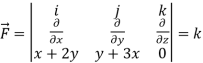 
Now,
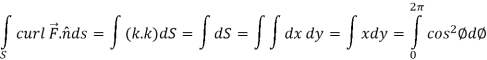
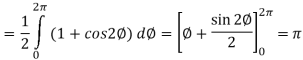
Hence the Stoke’s theorem is verified.
Q9) Define Gauss divergence theorem.
A9)
If V is the volume bounded by a closed surface S and 
is a vector point function with continuous derivative-
Then it can be written as-
Where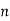
unit vector to the surface S.
Q10) Prove the following by using Gauss divergence theorem-
1. 
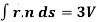
2. 
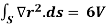
Where S is any closed surface having volume V and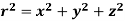 
A10)
Here we have by Gauss divergence theorem-
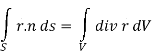
Where V is the volume enclose by the surface S.
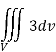
We know that-
= 3V
2.
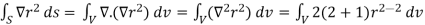
Because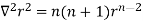 
Q11) Show that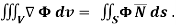 
A11)
By divergence theorem,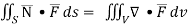 
..…(1)
Comparing this with the given problem let
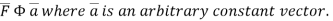
Hence, by (1)
………….(2)
Now ,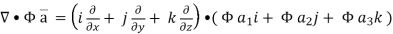
Hence, from (2), We get,
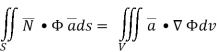
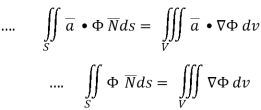
Q12) Prove that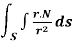 
=
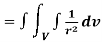
A12)
By Gauss Divergence Theorem,
=
=
=
.[
= 
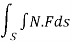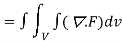
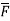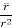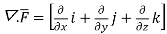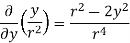
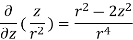
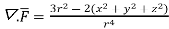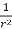
Q13) Apply Green’s theorem to evaluate 
where C is the boundary of the area enclosed by the x-axis and the upper half of circle 
A13)
We know that by Green’s theorem-
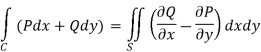
And it it given that-
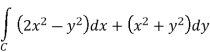
Now comparing the given integral-
P =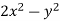 
and Q =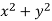 
Now-
and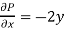 
So that by Green’s theorem, we have the following integral-
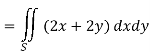
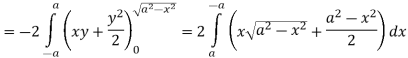
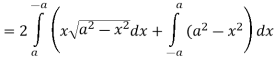
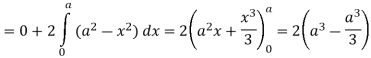
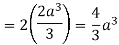
Q14) Evaluate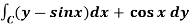 
by using Green’s theorem, where C is a triangle formed by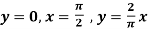 
A14)
First we will draw the figure-
Here the vertices of triangle OED are (0,0), (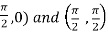
Now by using Green’s theorem-
Here P = y – sinx, and Q =cosx
So that-
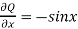and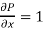
Now-
= 
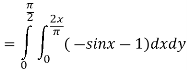
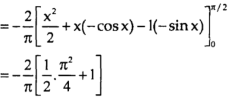
Which is the required answer.
Q15) Verify green’s theorem in xy-plane for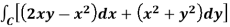 
where C is the boundary of the region enclosed by 
A15)
On comparing with green’s theorem,
We get-
P = 
and Q = 
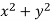
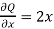and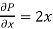 
By using Green’s theorem-
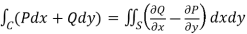………….. (1)
And left hand side= 
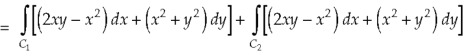………….. (2)
Now,
Along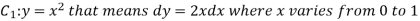 
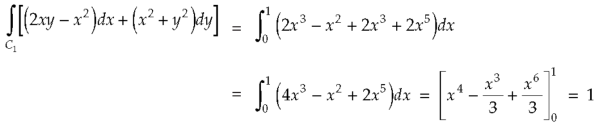
Along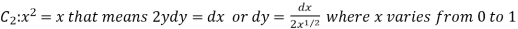 
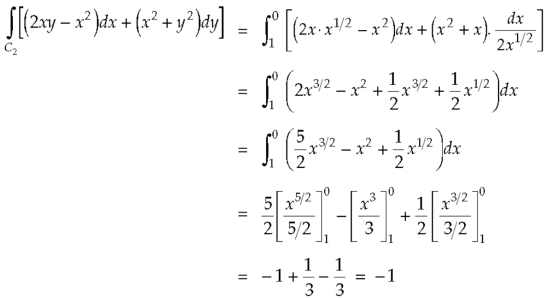
Put these values in (2), we get-
L.H.S. = 1 – 1 = 0
So that the Green’s theorem is verified.
