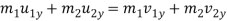Unit - 4
D'Alembert’s Principle
Q1) A pendulum bob has a mass of 10 kg and released from rest when 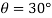 as shown in fig. Determine the tension in the chord at
as shown in fig. Determine the tension in the chord at 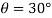 . Neglect the size of bob
. Neglect the size of bob
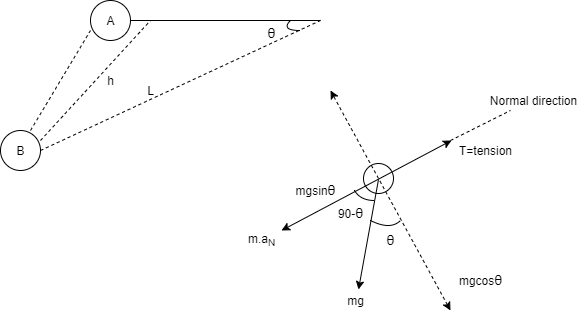
A1)
h = L sin
Consider the pendulum is initially at A and when it is released it occupies new position at B.
 = angle displaced
= angle displaced
L = Length of string of pendulum = radius of curvature =  {rho}
{rho}
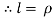
Now at point B apply D’- Alemberts Principle in normal direction ∑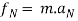
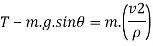
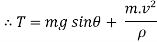
Here,
V = velocity at B = 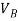
 Using equation of motion
Using equation of motion
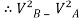 = 2gs
= 2gs
∴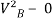 = 2gh
= 2gh
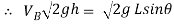
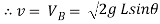
 ……….. Put in equation 1
……….. Put in equation 1
We get,
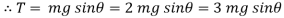
At
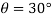
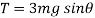
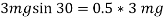 N
N
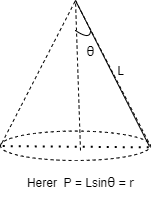
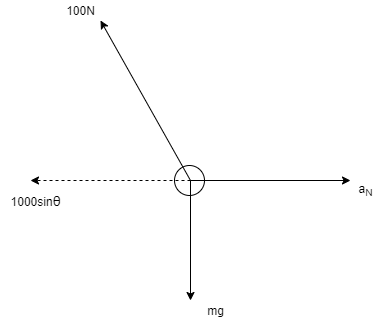
Q2) A 0.5 kg balls revolves in horizontal circle as shown in figure. If L = 1m and maximum allowable tension in the string is 100N determine maximum allowable speed and corresponding angle 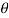 .
.
A2)
Consider the body diagram of ball as shown in figure
Apply D’-ALEMBERTS principle in x direction
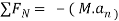
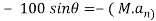
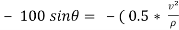 )
)
∴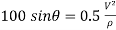
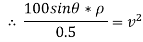
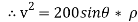
 …………… (1)
…………… (1)
Apply D’- alemberts principle in y direction
∑
But as there is no velocity in y direction thus
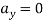
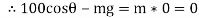
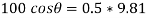
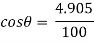
 …………………………. Put in equation 1.
…………………………. Put in equation 1.
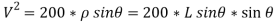
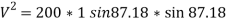
 = 199.52
= 199.52
Therefore,
V= 14.12 m/s
This is max allowable speed.
Q3) Two masses of 15 kg & 20 kg are moving along a straight line towards each other at velocities of 4 m/a & 2 m/s respectively. If e = 0.6, find the velocities of the masses immediately after the collision. Also find %in K.E. Due to impact.

A3)
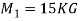
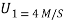
Let V1 &V2 are the velocities after collision , assume that both are towords right (  )
)
Using law of conservation of momentum,
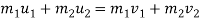
(15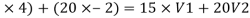
20 = 15V1+20V2 ………..(1)
Using coefficient of restitution
e = 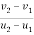
0.6 = 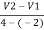
V2-V1= 0.6 6
6
V 2 – V 1 = 3.6
-V 1 + V2= 3.6 ……………(2)
Solving 1 & 2
15 V1 + 20 V2 = 20
-V1 + V2 = 3.6
We get V2= 2.11 m/s ( 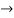 )
)
& V1 = - 1.43 m/s ( )
)
Loss in KE = initiak KE- final KE
Loss of K.E. = 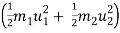 -
- 
= ( ½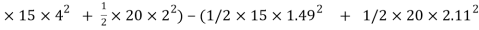
=(120+40) – (16.65+44.52 )
= 160 - 60.97
Loss in K.E = 99.029 joule.
% Loss in K.E. = 99.029/160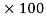
= 61.89%
Q4) The perfectly elastic balls 1, 2, 3 of masses 2kg 6kg 12kg respectively move along a line in same direction with velocities 12 m/s 4m/s and 2 m/s respectively. If the ball 1 strike the ball 2 which in horn strike ball 3 determine velocity of each ball after impact.

A4)
Given data
Ball 1
M1 = 2kg u1 = 12 m/s
Ball = 2
M2 = 6kg u = 4 m/s
Ball = 3
M3 = 12 kg u = 2 m/s
Consider the impact between ball 1 and ball2
For law of conversation of momentum
M1u1 + m2u2 = m1 v1 + m2v2
2*12 + 6*4 = 2v1 +6v2
48= 2v1 +6v2
2v1 + 6v2 = 48 - - - - - - - - - -- - - -- -eqn 1
As the balls are perfectly elastic
E=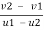 = 1
= 1
V2 – v1 = u2 – u1 = 12 -4 = 8
V2 – v1 = 8 - - - - - - - - - - - - - - - - - -eqn 2
Solving eqn 1 and 2
V1 = 0 and v2 = 8 m/s
As the ball strike each other ball 1 comes to rest and ball 2 moves forward ball s with new velocity of 8 m/s
U2 = 8 m/s
B) consider the impact between the ball 2 and 3
M2 u2 + m3 u3 = m2v2 + m3v3
6* 8 + 12*2 = 6V2 + 12v3
6V2 + 12 v3 = 72 ---------------- eqn 3
Are perfectly elastic balls
e = 1 =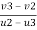 =
= 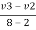
-V2 + v3 = 6 ------------------------ eqn 4
Solving equation 3 and 4 we get
V2 = 0 and v3 =6 m/s
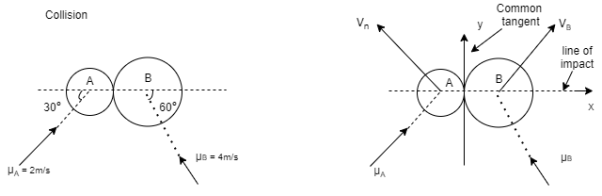
Q5) Two smooth balls A & B having mass of 4 kg and 8 kg respectively collider with initial velocities as shown in figure. If coefficient of restitution is e = 0.8, find the velocities of each ball after the collision.
A5)
Ball – A
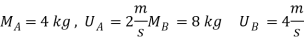
Using law of conservation of momentum along  direction
direction
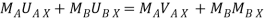
( 4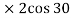 ) + ( 8
) + ( 8 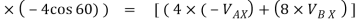
6.928 + (-16) = - 
- 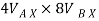 = -9.072 - - - - - - - -----1
= -9.072 - - - - - - - -----1
Coefficient of restitution
e = 0.8
0.8 = VB X + VA X /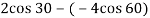
VB X + VA X= 2.986 ---------------------2
Solving 1 & 2 we get
VB X = 0.239 m/s
VA X= 2.746 m/s
Similarly, now component of velocity before and after the impact is conserved i.e. remain constant along the common tangent
V AY = UAY =  = 1 m/s
= 1 m/s
V BY= U B Y =4 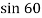 = 3.46 m/s
= 3.46 m/s
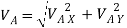 =
= 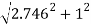 = 2.92 m/s
= 2.92 m/s
 =
= = 3.468 m/s
= 3.468 m/s
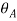 =20
=20
 = 086.05
= 086.05
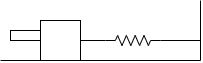
Q6) A 20 gm bullet horizontally into 300 gm block, which rest on smooth surface . after impact the bullet percentage into black the block moves to the right through 300 mm before momentarily coming to rest. Determine speed of bullet as it strike the block the block is resting on smooth surface against the spring which is originally upstretched & has a constant of 200 n/m
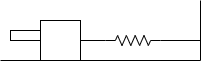
A6)
Given data
For bullet
M1 =0.02kg, u=?
For block,
m2 = 0.3 kg, u2 = 0
As the bullet penetrates into the block after the impact
The impact is perfectly plastic
After impact velocity of block & bullet will be equal,
V = V2 = V1 = common velocity
By applying law of conservation of momentum, for impact
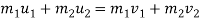
0.02 u 1 +0.3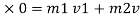
0.02 u 1 = ( m1 + m2 )v
0.02 u 1 = (0.02 + 0.3) v
0.02U 1 = 0.32 v
As the impact takes place, the black along with bullet will move toward right against spring force before coming to rest here spring will be compressed by 300 mm
Applying work energy principal just after the impact,
Total w.d= ke2 – ke 1
w.d. By spring force = KE 2 – KE 1
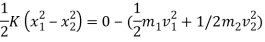
½ 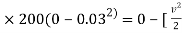 (0.02+0.3) ]
(0.02+0.3) ]
-9 = - 0.16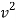
V = 7.5 m/s - ------ put this is in equation 1
0.02 u 1 = 0.32 v1 = 0.32 7.5
7.5
U 1 = 120 m/s - - - - -speed of the bullet as it strikes the block
Q7) A 100 gm ball dropped from a height of 600 mm on a small plate .it rebounds to a height of 400 mm when plate is directly resting on ground floor and it rebounded to a height of 250 mm when foam rubber matt is placed between plate and ground determine the coefficient of restitution between the plate and ground.
A7)
Case 1 = 600 mm
= 600 mm
 = 400 mm
= 400 mm
e =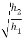
e = 
e = 0.816
Case 2
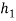 = 600 mm
= 600 mm
 = 250 mm
= 250 mm
e = 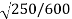
e = 0.645.
Q8) Explain impact and its types.
A8)
It is the collision between two bodies, which occurs for a very small-time interval. During this small-time interval both bodies will exert large amount on each other.
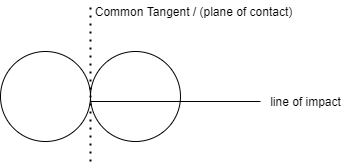
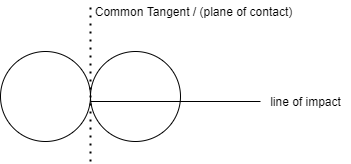
1] Line of impact:
It is the common normal to plane of contact. Or It is the common normal to the surface of two bodies in contact during impact.
It is perpendicular to common tangent.
2] Direct impact:
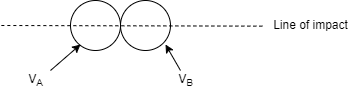
When the velocity of two bodies are along the line of impact then impute is said to be direct impact both partial are moving along the line of impact.

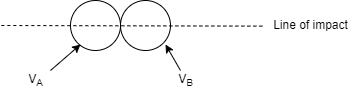
3] Oblique impact:
When both particle does not move along the line of impact, i.e. when velocities are not along the line of impact then it is called as oblique impact.
4] Central Impact:
When mass centres of two colliding bodies lie on the line of impact, the impact is called as central impact.

5] Non central impact:
When mass centres (c.g.) of the two colliding bodies do not lie on the line of impact, it is known to be non-central impact.
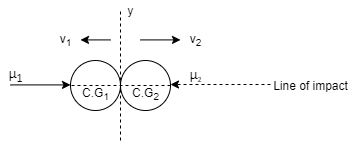
6] Direct central impact:
When the velocities of the two colliding bodies and their mass centre lies on the line of impact, then it is called as direct central impact.
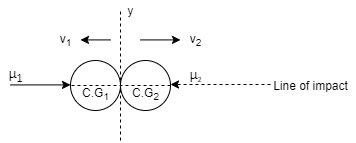
7] Oblique central impact
When the mass centres (C.G) of the two colliding bodies lies on the same line of impact but their velocities do not lie on the line of impact, then the impact is called as oblique central impact .
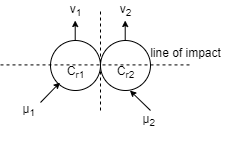
As par the law of conservation,
Component of total momentum of two bodies along the line of impact is given by–
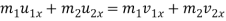
Component of momentum along the common tangent is
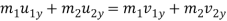
Unit - 4
D'Alembert’s Principle
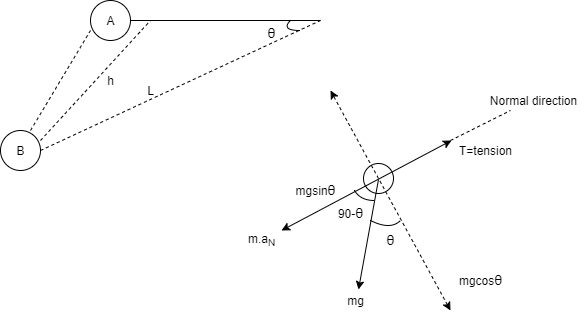
Q1) A pendulum bob has a mass of 10 kg and released from rest when  as shown in fig. Determine the tension in the chord at
as shown in fig. Determine the tension in the chord at  . Neglect the size of bob
. Neglect the size of bob
A1)
h = L sin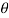
Consider the pendulum is initially at A and when it is released it occupies new position at B.
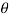 = angle displaced
= angle displaced
L = Length of string of pendulum = radius of curvature = 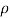 {rho}
{rho}
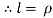
Now at point B apply D’- Alemberts Principle in normal direction ∑
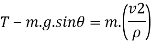
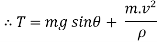
Here,
V = velocity at B = 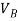
 Using equation of motion
Using equation of motion
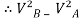 = 2gs
= 2gs
∴ = 2gh
= 2gh
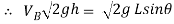
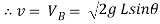
 ……….. Put in equation 1
……….. Put in equation 1
We get,
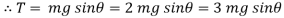
At
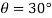
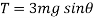
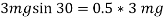 N
N
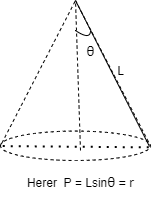
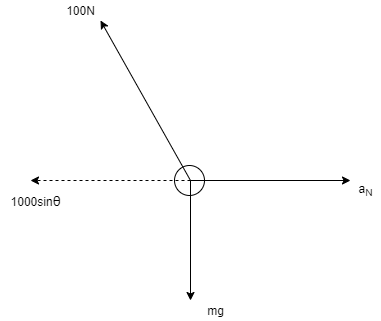
Q2) A 0.5 kg balls revolves in horizontal circle as shown in figure. If L = 1m and maximum allowable tension in the string is 100N determine maximum allowable speed and corresponding angle 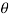 .
.
A2)
Consider the body diagram of ball as shown in figure
Apply D’-ALEMBERTS principle in x direction
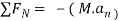
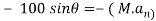
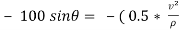 )
)
∴
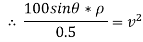
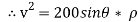
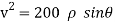 …………… (1)
…………… (1)
Apply D’- alemberts principle in y direction
∑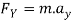
But as there is no velocity in y direction thus
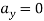
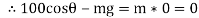
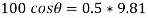
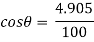
 …………………………. Put in equation 1.
…………………………. Put in equation 1.
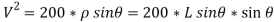
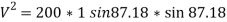
 = 199.52
= 199.52
Therefore,
V= 14.12 m/s
This is max allowable speed.
Q3) Two masses of 15 kg & 20 kg are moving along a straight line towards each other at velocities of 4 m/a & 2 m/s respectively. If e = 0.6, find the velocities of the masses immediately after the collision. Also find %in K.E. Due to impact.

A3)
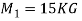
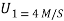
Let V1 &V2 are the velocities after collision , assume that both are towords right (  )
)
Using law of conservation of momentum,
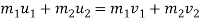
(15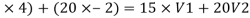
20 = 15V1+20V2 ………..(1)
Using coefficient of restitution
e = 
0.6 = 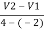
V2-V1= 0.6 6
6
V 2 – V 1 = 3.6
-V 1 + V2= 3.6 ……………(2)
Solving 1 & 2
15 V1 + 20 V2 = 20
-V1 + V2 = 3.6
We get V2= 2.11 m/s (  )
)
& V1 = - 1.43 m/s ( )
)
Loss in KE = initiak KE- final KE
Loss of K.E. =  -
- 
= ( ½
=(120+40) – (16.65+44.52 )
= 160 - 60.97
Loss in K.E = 99.029 joule.
% Loss in K.E. = 99.029/160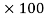
= 61.89%
Q4) The perfectly elastic balls 1, 2, 3 of masses 2kg 6kg 12kg respectively move along a line in same direction with velocities 12 m/s 4m/s and 2 m/s respectively. If the ball 1 strike the ball 2 which in horn strike ball 3 determine velocity of each ball after impact.

A4)
Given data
Ball 1
M1 = 2kg u1 = 12 m/s
Ball = 2
M2 = 6kg u = 4 m/s
Ball = 3
M3 = 12 kg u = 2 m/s
Consider the impact between ball 1 and ball2
For law of conversation of momentum
M1u1 + m2u2 = m1 v1 + m2v2
2*12 + 6*4 = 2v1 +6v2
48= 2v1 +6v2
2v1 + 6v2 = 48 - - - - - - - - - -- - - -- -eqn 1
As the balls are perfectly elastic
E= = 1
= 1
V2 – v1 = u2 – u1 = 12 -4 = 8
V2 – v1 = 8 - - - - - - - - - - - - - - - - - -eqn 2
Solving eqn 1 and 2
V1 = 0 and v2 = 8 m/s
As the ball strike each other ball 1 comes to rest and ball 2 moves forward ball s with new velocity of 8 m/s
U2 = 8 m/s
B) consider the impact between the ball 2 and 3
M2 u2 + m3 u3 = m2v2 + m3v3
6* 8 + 12*2 = 6V2 + 12v3
6V2 + 12 v3 = 72 ---------------- eqn 3
Are perfectly elastic balls
e = 1 = =
= 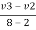
-V2 + v3 = 6 ------------------------ eqn 4
Solving equation 3 and 4 we get
V2 = 0 and v3 =6 m/s
Q5) Two smooth balls A & B having mass of 4 kg and 8 kg respectively collider with initial velocities as shown in figure. If coefficient of restitution is e = 0.8, find the velocities of each ball after the collision.
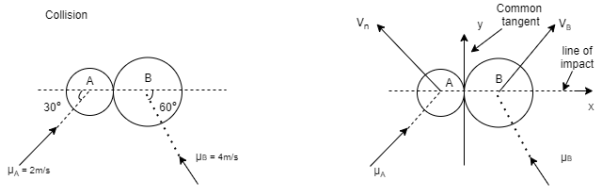
A5)
Ball – A
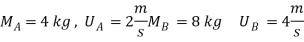
Using law of conservation of momentum along  direction
direction
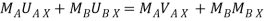
( 4 ) + ( 8
) + ( 8 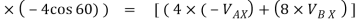
6.928 + (-16) = - 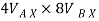
- 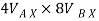 = -9.072 - - - - - - - -----1
= -9.072 - - - - - - - -----1
Coefficient of restitution
e = 0.8
0.8 = VB X + VA X /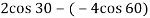
VB X + VA X= 2.986 ---------------------2
Solving 1 & 2 we get
VB X = 0.239 m/s
VA X= 2.746 m/s
Similarly, now component of velocity before and after the impact is conserved i.e. remain constant along the common tangent
V AY = UAY = 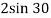 = 1 m/s
= 1 m/s
V BY= U B Y =4 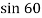 = 3.46 m/s
= 3.46 m/s
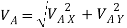 =
= 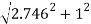 = 2.92 m/s
= 2.92 m/s
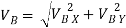 =
=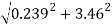 = 3.468 m/s
= 3.468 m/s
 =20
=20
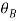 = 086.05
= 086.05
Q6) A 20 gm bullet horizontally into 300 gm block, which rest on smooth surface . after impact the bullet percentage into black the block moves to the right through 300 mm before momentarily coming to rest. Determine speed of bullet as it strike the block the block is resting on smooth surface against the spring which is originally upstretched & has a constant of 200 n/m
A6)
Given data
For bullet
M1 =0.02kg, u=?
For block,
m2 = 0.3 kg, u2 = 0
As the bullet penetrates into the block after the impact
The impact is perfectly plastic
After impact velocity of block & bullet will be equal,
V = V2 = V1 = common velocity
By applying law of conservation of momentum, for impact
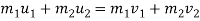
0.02 u 1 +0.3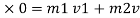
0.02 u 1 = ( m1 + m2 )v
0.02 u 1 = (0.02 + 0.3) v
0.02U 1 = 0.32 v
As the impact takes place, the black along with bullet will move toward right against spring force before coming to rest here spring will be compressed by 300 mm
Applying work energy principal just after the impact,
Total w.d= ke2 – ke 1
w.d. By spring force = KE 2 – KE 1
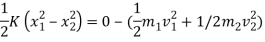
½ 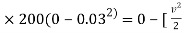 (0.02+0.3) ]
(0.02+0.3) ]
-9 = - 0.16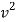
V = 7.5 m/s - ------ put this is in equation 1
0.02 u 1 = 0.32 v1 = 0.32 7.5
7.5
U 1 = 120 m/s - - - - -speed of the bullet as it strikes the block
Q7) A 100 gm ball dropped from a height of 600 mm on a small plate .it rebounds to a height of 400 mm when plate is directly resting on ground floor and it rebounded to a height of 250 mm when foam rubber matt is placed between plate and ground determine the coefficient of restitution between the plate and ground.
A7)
Case 1 = 600 mm
= 600 mm
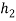 = 400 mm
= 400 mm
e =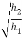
e = 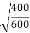
e = 0.816
Case 2
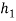 = 600 mm
= 600 mm
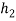 = 250 mm
= 250 mm
e = 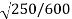
e = 0.645.
Q8) Explain impact and its types.
A8)
It is the collision between two bodies, which occurs for a very small-time interval. During this small-time interval both bodies will exert large amount on each other.
1] Line of impact:
It is the common normal to plane of contact. Or It is the common normal to the surface of two bodies in contact during impact.
It is perpendicular to common tangent.
2] Direct impact:
When the velocity of two bodies are along the line of impact then impute is said to be direct impact both partial are moving along the line of impact.

3] Oblique impact:
When both particle does not move along the line of impact, i.e. when velocities are not along the line of impact then it is called as oblique impact.
4] Central Impact:
When mass centres of two colliding bodies lie on the line of impact, the impact is called as central impact.

5] Non central impact:
When mass centres (c.g.) of the two colliding bodies do not lie on the line of impact, it is known to be non-central impact.
6] Direct central impact:
When the velocities of the two colliding bodies and their mass centre lies on the line of impact, then it is called as direct central impact.
7] Oblique central impact
When the mass centres (C.G) of the two colliding bodies lies on the same line of impact but their velocities do not lie on the line of impact, then the impact is called as oblique central impact .
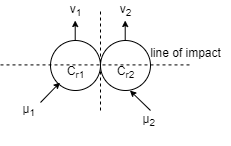
As par the law of conservation,
Component of total momentum of two bodies along the line of impact is given by–
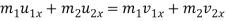
Component of momentum along the common tangent is