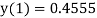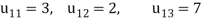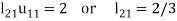Unit - 1
Numerical Methods
Q1) Define algebraic and transcedental equations.
A1)
Algebraic Equation: If f(x) is a pure polynomial, then the equation 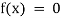 is called an algebraic equation in x.
is called an algebraic equation in x.
Ex: 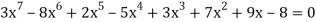
Transcendental Equation: If f(x) is an expression contain function as trigonometric, exponential and logarithmic etc. Then 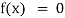 is called transcendental equation.
is called transcendental equation.
Ex 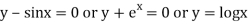
Q2) Using Newton-Raphson method, find a root of the following equation correct to 3 decimal places: .
.
A2)
Given 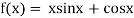
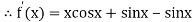
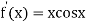
By Newton Raphson Method
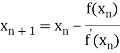
= 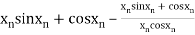
=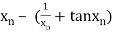
The initial approximation is  in radian.
in radian.
For n =0, the first approximation 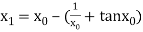
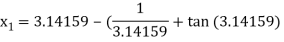
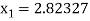
For n =1, the second approximation 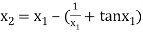
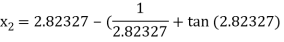
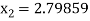
For n =2, the third approximation 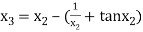

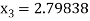
For n =3, the fourth approximation 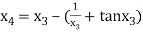
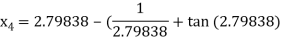
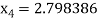
Hence the root of the given equation correct to five decimal place 2.79838.
Q3) Using Newton-Raphson method, find a root of the following equation correct to 4 decimal places: 
A3)
Let 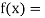

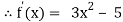
By Newton Raphson Method
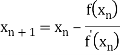
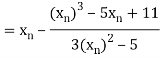

Let the initial approximation be 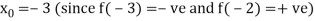
For n=0, the first approximation 
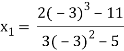
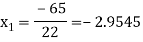
For n=1, the second approximation 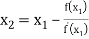

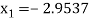
For n=2, the third approximation 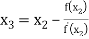
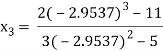
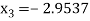
Since 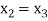 therefore the root of the given equation correct to four decimal places is -2.9537
therefore the root of the given equation correct to four decimal places is -2.9537
Q4) What is the method of false position?
A4)
This is the oldest method of finding the approximate numerical value of a real root of an equation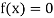 .
.
In this method we suppose that 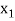 and
and 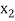 are two points where
are two points where 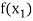 and
and 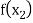 are of opposite sign .Let
are of opposite sign .Let 
Hence the root of the equation 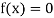 lies between
lies between 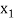 and
and 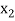 and so,
and so, 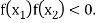
The Regula Falsi formula
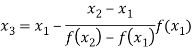
Find 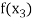 is positive or negative. If
is positive or negative. If 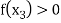 then root lies between
then root lies between  and
and 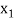 or if
or if  then root lies between
then root lies between 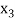 and
and 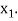 similarly we calculate
similarly we calculate 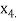
Q5) Find a real root of the equation 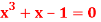 near
near , correct to three decimal place by the Regula Falsi method.
, correct to three decimal place by the Regula Falsi method.
A5)
Let 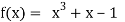
Now, 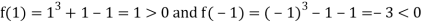
And also 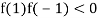
Hence the root of the equation  lies between
lies between 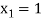 and
and 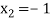 and so,
and so, 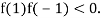
By Regula Falsi Mehtod
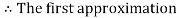
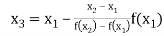
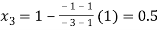
Now, 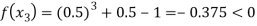
So the root of the equation 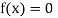 lies between 1 and 0.5 and so
lies between 1 and 0.5 and so 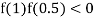
By Regula Fasli Method
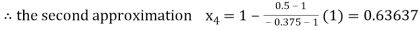
Now, 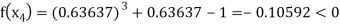
So the root of the equation  lies between 1 and 0.63637 and so
lies between 1 and 0.63637 and so 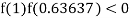
By Regula Fasli Method
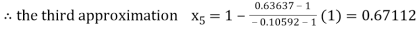
Now, 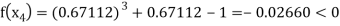
So the root of the equation 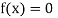 lies between 1 and 0.67112 and so
lies between 1 and 0.67112 and so 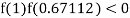
By Regula Fasli Method
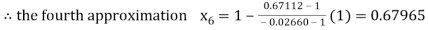
Now, 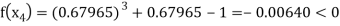
So the root of the equation 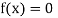 lies between 1 and 0.63636 and so
lies between 1 and 0.63636 and so 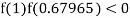
By Regula Fasli Method
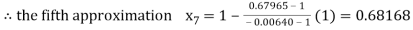
Now, 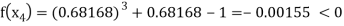
So the root of the equation 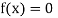 lies between 1 and 0.68168 and so
lies between 1 and 0.68168 and so 
By Regula Fasli Method
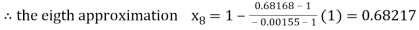
Now, 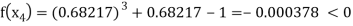
Hence the approximate root of the given equation near to 1 is 0.68217
Q6) Find the real root of the equation

By the method of false position correct to four decimal places
A6)
Let 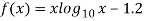
By hit and trail method

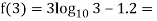 0.23136 > 0
0.23136 > 0
So, the root of the equation 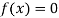 lies between
lies between 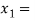 2 and
2 and 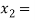 3 and also
3 and also 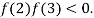
By Regula Falsi Mehtod

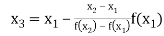
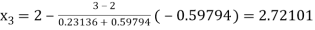
Now, 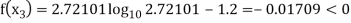
So, root of the equation 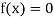 lies between 2.72101 and 3 and also
lies between 2.72101 and 3 and also 
By Regula Falsi Mehtod
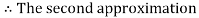

Now, 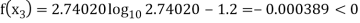
So, root of the equation  lies between 2.74020 and 3 and also
lies between 2.74020 and 3 and also 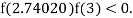
By Regula Falsi Mehtod

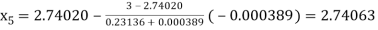
Now, 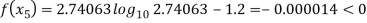
So, root of the equation  lies between 2.74063 and 3 and also
lies between 2.74063 and 3 and also 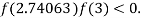
By Regula Falsi Mehtod
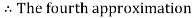
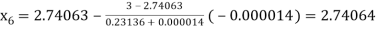
Hence the root of the given equation correct to four decimal places is 2.7406
Q7) Solve the equations-
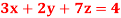
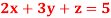
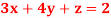
A7)
Let

So that-
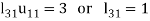
3. 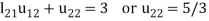
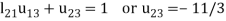
4. 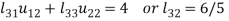
5. 
So

Thus-
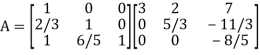
Writing UX = V,
The system of given equations become-
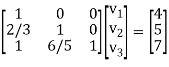
By solving this-
We get-
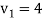
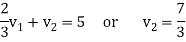
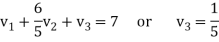
Therefore the given system becomes-
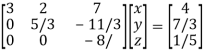
Which means-
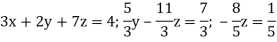
By back substitution, we have-
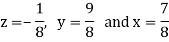
Q8) Solve ,
, 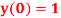 using Taylor’s series method and compute
using Taylor’s series method and compute 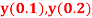 .
.
A8)
Here 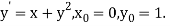 This implies that
This implies that 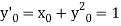 .
.
Differentiating, we get
 .
.
 .
.
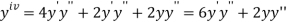
 .
.
The Taylor’s series at  ,
,
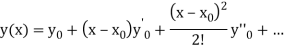
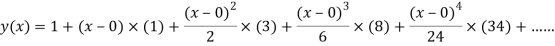
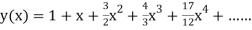 (1)
(1)
At 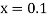 in equation (1) we get
in equation (1) we get
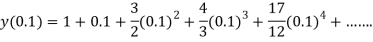
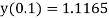
At 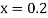 in equation (1) we get
in equation (1) we get

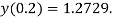
Q9) Solve 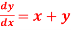 numerically, start from
numerically, start from 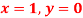 and carry to
and carry to  using Taylor’s series method.
using Taylor’s series method.
A9)
Here 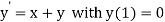 .
.
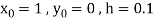
We have 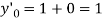
Differentiating, we get
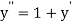 implies that
implies that 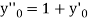 or
or 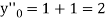
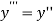 implies that
implies that 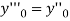 or
or 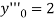 .
.
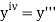 implies that
implies that 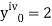
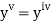 implies that
implies that 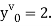
The Taylor’s series at 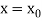 ,
,
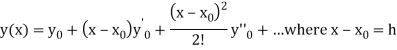
Or 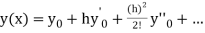
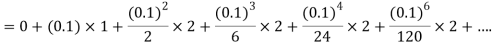
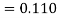
Here 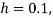
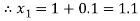
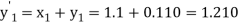
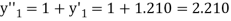

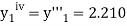
The Taylor’s series
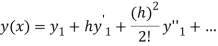

 .
.
Q10) Using Euler’s method solve the differential equation for y at x=1 in five steps
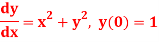
A10)
Given equation 
Here 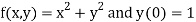
No. Of steps n=5 and so that 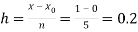
So that 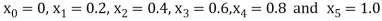
Also 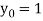
By Euler’s formula
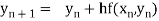 , n=0,1,2,3,4 ……(i)
, n=0,1,2,3,4 ……(i)
For n=0 in equation (i) we get
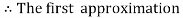

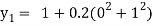
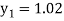
For n=1 in equation (i) we get
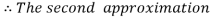
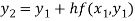
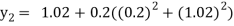
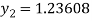
For n=2 in equation (i) we get
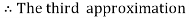
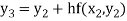
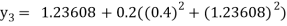
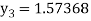
For n=3 in equation (i) we get
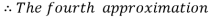
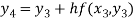
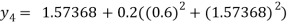
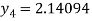
For n=4 in equation (i) we get
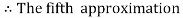
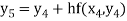


Hence 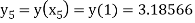
Q11) Use modified Euler’s method to compute y for x=0.05. Given that

Result correct to three decimal places.
A11)
Given equation 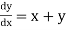
Here 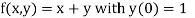
Take h = 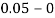 = 0.05
= 0.05
By modified Euler’s formula the initial iteration is
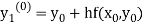
 )
)
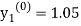
The iteration formula by modified Euler’s method is
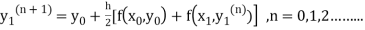 -----(i)
-----(i)
For n=0 in equation (i) we get
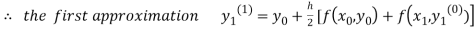
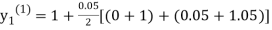
Where 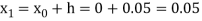 and
and 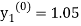 as above
as above

For n=1 in equation (i) we get
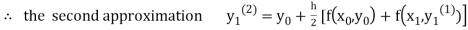
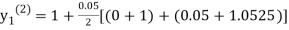

For n=3 in equation (i) we get

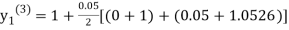
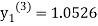
Since third and fourth approximation are equal .
Hence y=1.0526 at x = 0.05 correct to three decimal places.
Q12) Use Runge Kutta method to find y when x=1.2 in step of h=0.1 given that
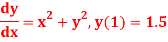
A12)
Given equation 
Here 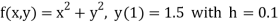
Also 
By Runge Kutta formula for first interval
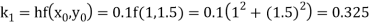
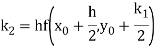
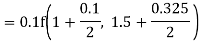


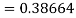

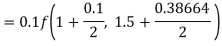
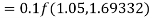
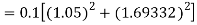
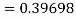
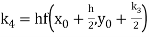



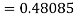
Again 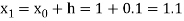
A fourth order Runge Kutta formula:
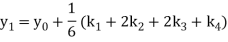

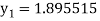
To find y at 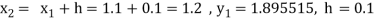

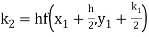
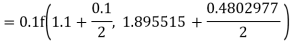
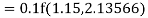
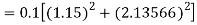
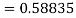
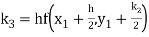
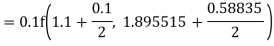
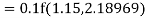
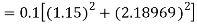
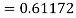
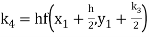
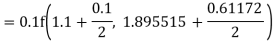
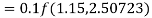
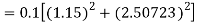
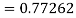
A fourth order Runge Kutta formula:
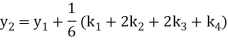

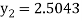
Q13) Using Runge Kutta method of fourth order, solve

A13)
Given equation 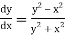
Here 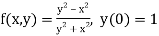
Also 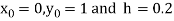
By Runge Kutta formula for first interval

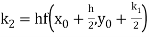
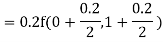
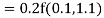
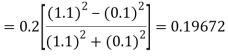
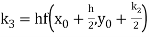
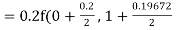 )
)
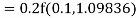

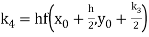

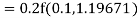
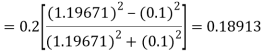
A fourth order Runge Kutta formula:
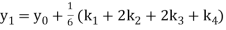
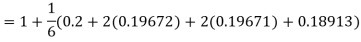

Hence at x = 0.2 then y = 1.196
To find the value of y at x=0.4. In this case 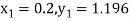
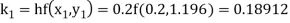

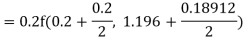
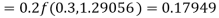

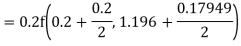

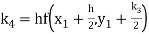

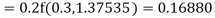
A fourth order Runge Kutta formula:

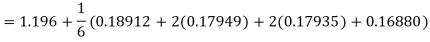

Hence at x = 0.4 then y=1.37527
Q14) Using Runge Kutta method of order four, solve  to find
to find 
A14)
Given second order differential equation is
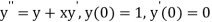
Let 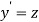 then above equation reduces to
then above equation reduces to
Or 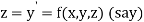
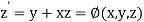 (say)
(say)
Or 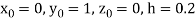 .
.
By Runge Kutta Method we have
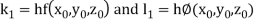

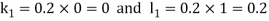
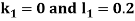

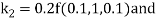
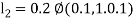



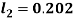
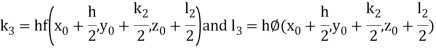
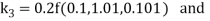

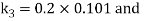
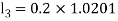
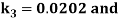
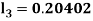


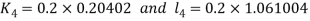
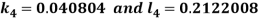
A fourth order Runge Kutta formula:
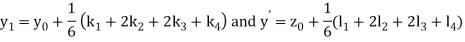
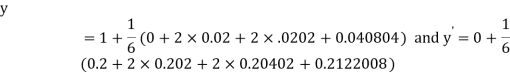

Q15) Solve the differential equations
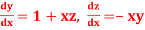 for
for 
A15)
Using four order Runge Kutta method with initial conditions 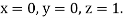
Given differential equation are
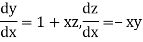
Let 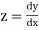
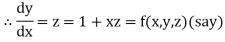
And 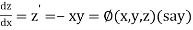
Also 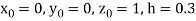
By Runge Kutta Method we have
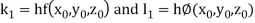
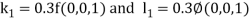
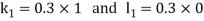


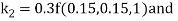
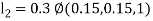
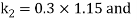
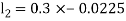
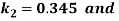
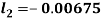
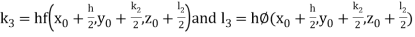
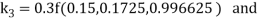
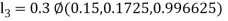
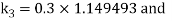
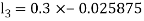
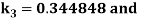
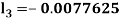
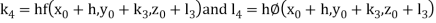
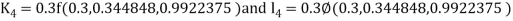
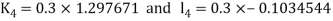
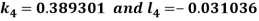
A fourth order Runge Kutta formula:

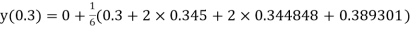
And 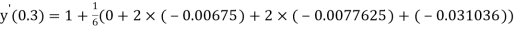
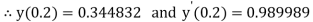 .
.
Q16) Find the solution of the differential equation 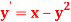 in the range
in the range  for the boundary conditions y = 0 and x = 0 by using Milne’s method.
for the boundary conditions y = 0 and x = 0 by using Milne’s method.
A16)
By using Picards method-
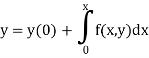
Where
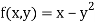
To get the first approximation-
We put y = 0 in f(x, y),
Giving-
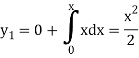
In order to find the second approximation, we put y = 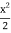 in f(x,y)
in f(x,y)
Giving-
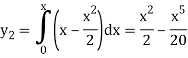
And the third approximation-
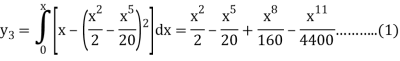
Now determine the starting values of the Milne’s method from equation (1), by choosing h = 0.2
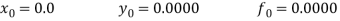
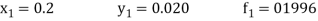
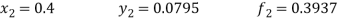
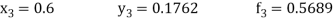
Now using the predictor-
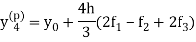
X = 0.8
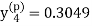 ,
, 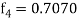
And the corrector-
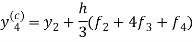
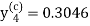 ,
,  ................(2)
................(2)
Now again using corrector-
Using predictor-

X = 1.0,
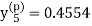 ,
, 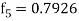
And the corrector-

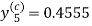 ,
, 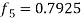
Again using corrector-
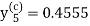 , which is same as before
, which is same as before
Hence