Unit - 4
Statistical techniques
Q1) Define positive correlation.
A1)
Correlation between two variables is said to be positive if the values of the variables deviate in the same direction i.e. if the values of one variable increase (or decrease) then the values of other variable also increase (or decrease). For example:
1. Heights and weights of group of persons;
2. House hold income and expenditure;
3. Amount of rainfall and yield of crops
Q2) What is Karl Pearson’s coefficient of correlation?
A2)
Coefficient of correlation measures the intensity or degree of linear relationship between two variables. It was given by British Biometrician Karl Pearson (1867-1936).
Karl Pearson’s Coefficient of Correlation is widely used mathematical method is used to calculate the degree and direction of the relationship between linear related variables. The coefficient of correlation is denoted by “r”.
If X and Y are two random variables then correlation coefficient between X and Y is denoted by r and defined as-
Karl Pearson’s coefficient of correlation-

Here-  and
and 
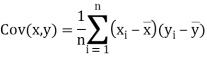
Q3) Find the correlation coefficient between Age and weight of the following data-
Age | 30 | 44 | 45 | 43 | 34 | 44 |
Weight | 56 | 55 | 60 | 64 | 62 | 63 |
A3)
x | Y | 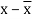 | 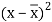 | 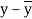 |  | ( 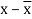 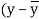 |
30 | 56 | -10 | 100 | -4 | 16 | 40 |
44 | 55 | 4 | 16 | -5 | 25 | -20 |
45 | 60 | 5 | 25 | 0 | 0 | 0 |
43 | 64 | 3 | 9 | 4 | 16 | 12 |
34 | 62 | -6 | 36 | 2 | 4 | -12 |
44 | 63 | 4 | 16 | 3 | 9 | 12 |
Sum= 240 |
360 |
0 |
202 |
0 |
70
|
32 |
Karl Pearson’s coefficient of correlation-
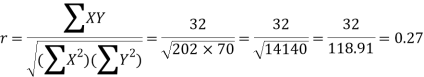
Here the correlation coefficient is 0.27.which is the positive correlation (weak positive correlation), this indicates that the as age increases, the weight also increase.
Q4) Psychological tests of intelligence and of engineering ability were applied to 10 students. Here is a record of ungrouped data showing intelligence ratio (I.R) and engineering ratio (E.R). Calculate the co-efficient of correlation.
Student | A | B | C | D | E | F | G | H | I | J |
I.R | 105 | 104 | 102 | 101 | 99 | 98 | 96 | 92 | 93 | 92 |
E.R | 101 | 103 | 100 | 98 | 96 | 104 | 92 | 94 | 97 | 94 |
A4)
We construct the following table:
Student | Intelligence ratio x 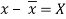 | Engineering ratio y 
| X2 | Y2 | XY |
A B C D E F G H I J | 100 6 104 5 102 3 101 2 100 1 99 0 98 -1 96 -3 93 -6 92 -7 | 101 3 103 5 100 2 98 0 95 -3 96 -2 104 6 92 -6 97 -1 94 -4 | 36 25 9 4 1 0 1 9 36 49 | 9 25 4 0 9 4 36 36 1 16 | 18 25 6 0 -3 0 -6 18 6 28 |
Total | 990 0 | 980 0 | 170 | 140 | 92 |
From this table, mean of 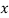 i.e.,
i.e., 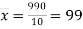 and mean of
and mean of 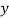 , i.e.,
, i.e.,
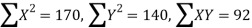
Substituting these values in the formula (1), we have
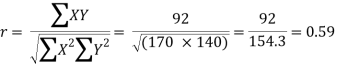
Q5) Three judges A, B, C, give the following ranks. Find which pair of judges has common approach
A | 1 | 6 | 5 | 10 | 3 | 2 | 4 | 9 | 7 | 8 |
B | 3 | 5 | 8 | 4 | 7 | 10 | 2 | 1 | 6 | 9 |
C | 6 | 4 | 9 | 8 | 1 | 2 | 3 | 10 | 5 | 7 |
A5)
Here 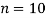
 | Ranks by  | 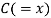 |  | 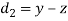 | 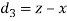 | 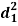 | 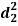 | 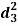 |
1 6 5 10 3 2 4 9 7 8 | 3 5 8 4 7 10 2 1 6 9 | 6 4 9 8 1 2 3 10 5 7 | -2 1 -3 6 -4 -8 2 8 1 -1 | -3 1 -1 -4 6 8 -1 -9 1 2 | 5 -2 4 -2 -2 0 -1 1 -2 -1 | 4 1 9 36 16 64 4 64 1 1 | 9 1 1 16 36 64 1 81 1 4 | 25 4 16 4 4 0 1 1 4 1 |
Total |
|
| 0 | 0 | 0 | 200 | 214 | 60 |
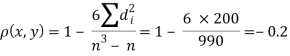
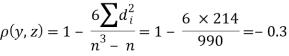
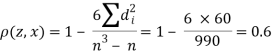
Since  is maximum, the pair of judges A and C have the nearest common approach.
is maximum, the pair of judges A and C have the nearest common approach.
Q6) Compute the Spearman’s rank correlation coefficient of the dataset given below-
Person | A | B | C | D | E | F | G | H | I | J |
Rank in test-1 | 9 | 10 | 6 | 5 | 7 | 2 | 4 | 8 | 1 | 3 |
Rank in test-2 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
A6)
Person | Rank in test-1 | Rank in test-2 | d = 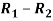 | 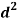 |
A | 9 | 1 | 8 | 64 |
B | 10 | 2 | 8 | 64 |
C | 6 | 3 | 3 | 9 |
D | 5 | 4 | 1 | 1 |
E | 7 | 5 | 2 | 4 |
F | 2 | 6 | -4 | 16 |
G | 4 | 7 | -3 | 9 |
H | 8 | 8 | 0 | 0 |
I | 1 | 9 | -8 | 64 |
J | 3 | 10 | -7 | 49 |
Sum |
|
|
| 280 |
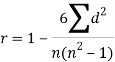
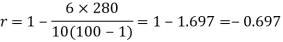
Q7) Calculate Spearman rank-order correlation
English | 56 | 75 | 45 | 71 | 62 | 64 | 58 | 80 | 76 | 61 |
Maths | 66 | 70 | 40 | 60 | 65 | 56 | 59 | 77 | 67 | 63 |
A7)
Rank by taking the highest value or the lowest value as 1.
Here, highest value is taken as 1
English | Maths | Rank (English) | Rank (Math) | d | d2 |
56 | 66 | 9 | 4 | 5 | 25 |
75 | 70 | 3 | 2 | 1 | 1 |
45 | 40 | 10 | 10 | 0 | 0 |
71 | 60 | 4 | 7 | -3 | 9 |
62 | 65 | 6 | 5 | 1 | 1 |
64 | 56 | 5 | 9 | -4 | 16 |
58 | 59 | 8 | 8 | 0 | 0 |
80 | 77 | 1 | 1 | 0 | 0 |
76 | 67 | 2 | 3 | -1 | 1 |
61 | 63 | 7 | 6 | 1 | 1 |
|
|
|
|
| 54 |
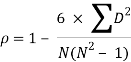
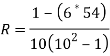
R = 0.67
Therefore, this indicates a strong positive relationship between the ranks individuals obtained in the math and English exam.
Q8) Explain regression.
A8)
If the scatter diagram indicates some relationship between two variables  and
and 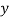 , then the dots of the scatter diagram will be concentrated round a curve. This curve is called the curve of regression. Regression analysis is the method used for estimating the unknown values of one variable corresponding to the known value of another variable.
, then the dots of the scatter diagram will be concentrated round a curve. This curve is called the curve of regression. Regression analysis is the method used for estimating the unknown values of one variable corresponding to the known value of another variable.
Regression is the measure of average relationship between independent and dependent variable
Regression can be used for two or more than two variables.
There are two types of variables in regression analysis.
1. Independent variable
2. Dependent variable
The variable which is used for prediction is called independent variable.
It is known as predictor or regressor.
The variable whose value is predicted by independent variable is called dependent variable or regressed or explained variable.
The scatter diagram shows relationship between independent and dependent variable, then the scatter diagram will be more or less concentrated round a curve, which is called the curve of regression.
When we find the curve as a straight line then it is known as line of regression and the regression is called linear regression.
Q9) Two variables X and Y are given in the dataset below, find the two lines of regression.
x | 65 | 66 | 67 | 67 | 68 | 69 | 70 | 71 |
y | 66 | 68 | 65 | 69 | 74 | 73 | 72 | 70 |
A9)
The two lines of regression can be expressed as-
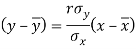
And
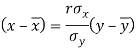
x | y |  |  | Xy |
65 | 66 | 4225 | 4356 | 4290 |
66 | 68 | 4356 | 4624 | 4488 |
67 | 65 | 4489 | 4225 | 4355 |
67 | 69 | 4489 | 4761 | 4623 |
68 | 74 | 4624 | 5476 | 5032 |
69 | 73 | 4761 | 5329 | 5037 |
70 | 72 | 4900 | 5184 | 5040 |
71 | 70 | 5041 | 4900 | 4970 |
Sum = 543 | 557 | 36885 | 38855 | 37835 |
Now-
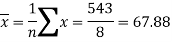
And
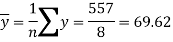
Standard deviation of x-
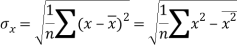

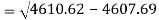

Similarly-
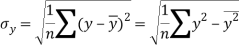
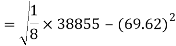
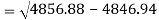
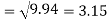
Correlation coefficient-
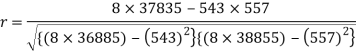



Put these values in regression line equation, we get
Regression line y on x-
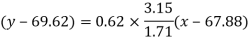
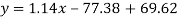
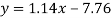
Regression line x on y-
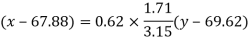
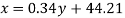
Q10) The following data give the experience of machine operators and their performance rating given by the number of good parts turned out per 100 pieces.
Operator: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
Experience: (in year) | 16 | 12 | 18 | 4 | 3 | 10 | 5 | 12 |
Performance: Rating | 87 | 88 | 89 | 68 | 78 | 80 | 75 | 83 |
Obtain the two regression equations and estimate the performance rating of an operator who has put 15 years in service.
A10)
We define the variables,
X: Experience | Y: Performance rating Table of calculations: | |||
X | Y | Xy | X2 | Y2 |
16 12 18 4 3 10 5 12 | 87 88 89 68 78 80 75 83 | 1392 1056 1602 272 232 800 375 996 | 256 144 324 16 9 100 25 144 | 7569 7744 7921 4624 6084 6400 5625 6889 |
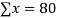 | 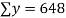 | 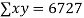 | 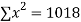 | 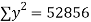 |
Now the two regression equations are,
(

Where,
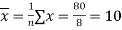 and
and 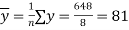
Also,
Co(x,y) 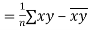
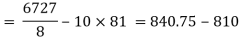
Co(x,y)=30.75

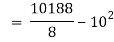
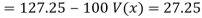
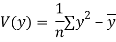
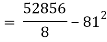
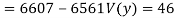
Now we find,
Regression co-efficient od X on Y
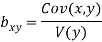

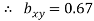 and
and
Regression xo-efficient of X on Y
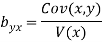

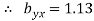
Now substituting the values of x , y , bxy and byx in the regression
Equations we get,
(x-10) = 0.67(y-81) -------x on y (i)
(y-81) =1.13(x-10) ------- y on x (ii)
As the two regression equations.
Now to estimate Performance rating (y) when Experience (x) = 15, we use the regression equation of y on x
(y-81) =1.13(15-10)
y = 81+ 5.65 = 86.65
Hence the estimated performance rating for the operator with 15 years of
Experience is approximately 86.65 i.e. approximately 87
Q11) Find the marks of a student in the Subject of Mathematics who have scored 65 marks in Accountancy Given,
Average marks in Mathematics Accountancy Standard Deviation of marks in Mathematics In accountancy | 70 80 8 10 |
Coefficient of correlation between the marks of Mathematics and marks of Accountancy is 0.64.
A11)
We define the variables,
X: Marks in Mathematics
Y: Marks in Accountancy
Therefore, we have,
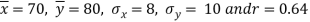
Now we want to approximate the marks in Mathematics (x), we obtain the
Regression equation of x on y, which is given by
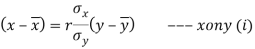
Substituting the values, we get,
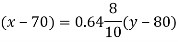
i.e. 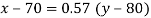
Therefore, when marks in Accountancy (Y) = 65
x- 70 = 0.57(65-80)
x = 70-2.85 = 67.15 i.e. 67 approx.
Substitute the value of a and b in the equation. Regression line of X on Y is 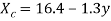
Q12) Find the means values of x,y and r from the two regression equations. 3x+2y-26=0 and sx+y-31=0. Also find sx when sy = 3.
A12)
The two regression equations are,
3x+2y-26=0 -------- (i)
6x+y-31=0 ----------(ii)
Now for x and y we solve the two equations as the simultaneous equations.
On solving (1) and (2), we get-
x = 4 and y = 7.
Now to find ‘r’ we express the equations in the form y=a+bx
So, from eqns (i) and (ii)
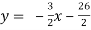 and
and 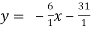

Since, b1 < b2 (i.e., b1 is smaller in number irrespective of sign + or -)
... Equation (i) is regression of  on
on  and
and 
Hence, eqn (ii) is regression of 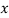 on
on 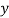 and
and 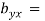 - 1/6 = - 0.16
- 1/6 = - 0.16
Now we find, 
Note: The sign of ‘r’ is same as the sign of regression coefficients
Now to find 6x when 6y = 3, we use the formula,
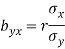
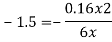
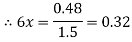
Hence means 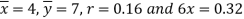
Q13) Calculate the regressive coefficients from the data given below:
| Series  | Series  |
|
Average | 25 | 22 |
|
Standard deviation | 4 | 2 | r=0.8 |
A13)
The coefficient of regression of y on x is
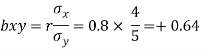
The coefficient of regression of y on x is
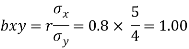
Q14) From the following regression equation, find means x , y ,and d ‘r’ 3x-2y-10 = 0, 24x-25y+145 = 0
A14)
The two regression equations are,
3x-2y-10=0(i)
24x-25y+145=0(ii)
Now for x and y we solve the two equations as the simultaneous equations.
Therefore, by (i) x 8 and (ii) x1, we get
24x-16y-80 = 0
24x-16y-80 = 0
24x-25y+145 = 0
9y-225=0y = 25
Putting y = 25 in eqn (i), we get
3x-2(25)-10 = 0
3x – 60=0
X = 20
Hence x= 20 and y= 25.
Now to find ‘r’ we express the equations in the form y=a+bx So, from eqns (i) and (ii)
B1=1.5 b2=0.96
Equation (ii) is regression of y on x and byx = 0.9
Hence eqn (i) is regression of x on y and bxy = 1/1.5 =0.67
Now we find, r = √ bxyXbyxi.e. r=√0.67x0.96= + 0.84
Q15) Fit the straight-line curve to the following data.
X | 75 | 80 | 93 | 65 | 87 | 71 | 98 | 68 | 84 | 77 |
Y | 82 | 78 | 86 | 72 | 91 | 80 | 95 | 72 | 89 | 74 |
A15)
First drawing the table,
X | Y |  | XY |
75 | 82 | 5625 | 1 |
80 | 78 | 6400 | 4 |
93 | 86 | 8349 | 9 |
65 | 72 | 4225 | 16 |
87 | 91 | 7569 | 25 |
71 | 80 | 5041 |
|
98 | 95 | 9605 |
|
68 | 72 | 4624 |
|
84 | 89 | 7056 |
|
77 | 74 | 5929 |
|
 | 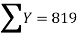 | 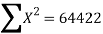 | 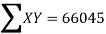 |
The normal equation are:
Σy = aΣx + nb
And
Σxy = aΣx2 + bΣx.
Substituting the values, we get,
819 = 798a + 10b
66045 = 64422a + 798b
Solving, we get
a = 0.9288 and b = 7.78155
Therefore, the straight line equation is:
y = 0.9288x + 7.78155.
Q16) Find the arithmetic mean of the following dataset.
Class | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
Frequency | 7 | 8 | 20 | 10 | 5 |
A16)
Let the assumed mean (a) = 25,
Class | Mid-value | Frequency | x – 25 = d | Fd |
0-10 | 5 | 7 | -20 | -140 |
10-20 | 15 | 8 | -10 | -80 |
20-30 | 25 | 20 | 0 | 0 |
30-40 | 35 | 10 | 10 | 100 |
40-50 | 45 | 5 | 20 | 100 |
Total |
| 50 |
| -20 |
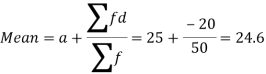
Q17) Calculate the first and third quartile of the following data-
Class interval | f |
0-10 | 3 |
10-20 | 5 |
20-30 | 7 |
30-40 | 9 |
40-50 | 4 |
A17)
Class interval | f | CF |
0-10 | 3 | 3 |
10-20 | 5 | 8 |
20-30 | 7 | 15 |
30-40 | 9 | 24 |
40-50 | 4 | 28 |
| N = 28 |
|
Here N/4 = 28/4 = 7
The 7th observation falls in the class 10-20. So, this is the first quartile class. 3N/4 = 21th observation falls in class 30-40, so it is the third quartile class.
For first quartile l = 10, f = 5, C = 3, N = 28
We know that-
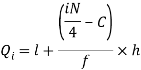

For third quartile l = 30, f = 9, C = 15

Q18) Find the quartile deviation of the following data.
Class interval | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
Frequency | 3 | 5 | 7 | 9 | 4 |
A18)
We have N/4 = 28/4 = 7 and 7th observation falls in the class 10-20.
This is the first quartile class. Similarly, 3N/4 = 21 and 21st observation falls in the interval 30-40. This is the third quartile class.
Class interval | f | CF |
0-10 | 3 | 3 |
10-20 | 5 | 8 |
20-30 | 7 | 15 |
30-40 | 9 | 24 |
40-50 | 4 | 28 |
| N = 28 |
|
By using the formula of quartile deviation, we will find 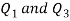 -
-
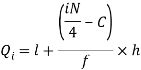
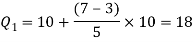
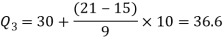
Therefore-
Q = ½ × (Q3 – Q1) = (36.67 – 18) / 2 = 9.335
Q19) The students of statistics got the marks as below- 16, 24, 13, 18, 15, 10, 23
Find the mean deviation from mean.
A19)
X | x-17 | |x-  |
16 | -1 | 1 |
24 | 7 | 7 |
13 | -4 | 4 |
18 | 1 | 1 |
15 | -2 | 2 |
10 | -7 | 7 |
23 | 6 | 6 |
Sum = 119 |
| 28 |
Then
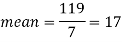
Hence

Q20) Suppose batsman A has mean 50 with SD 10. Batsman B has mean 30 with SD 3. What do you infer about their performance?
A20)
A has higher mean than B. This means A is a better run maker.
However, B has lower CV (3/30 = 0.1) than A (10/50 = 0.2) and is consequently more consistent.
Q21) Suppose a series of 100 data points has mean 50 and variance 20. Another series of 200 data points has mean 80 and variance 40. What is the combined variance of the given series?
A21)
The mean of the combined series-
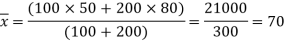
Therefore, d1= 50 – 70 = –20 and d2 = 80 – 70 =10
Variance of the combined series
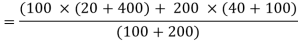
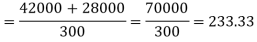
Q22) Calculate the standard deviation of the following frequency distribution-
Weight | 60 – 62 | 63 – 65 | 66 – 68 | 69 – 71 | 72 – 74 |
Item | 5 | 18 | 42 | 27 | 8 |
A22)
Weight | Item (f) | X | d = x – 67 | f.d | 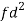 |
60 – 62 | 5 | 61 | -6 | -30 | 180 |
63 – 65 | 18 | 64 | -3 | -54 | 162 |
66 – 68 | 42 | 67 | 0 | 0 | 0 |
69 – 71 | 27 | 70 | 3 | 81 | 243 |
72 – 74 | 8 | 73 | 6 | 48 | 288 |
Total |
100 |
|
|
45 |
873 |
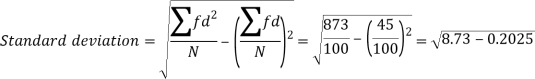
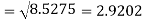
Q23) Calculate the coefficient of skewness from the following data:
Weight (lbs) | 70-80 | 80-90 | 90-100 | 100-110 | 110-120 | 120-130 | 130-140 | 140=150 |
No. Of persons | 12 | 18 | 35 | 42 | 50 | 45 | 20 | 8 |
A23)
Here total frequency 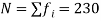
The cumulative frequency table is
Weight (lbs) | 70-80 | 80-90 | 90-100 | 100-110 | 110-120 | 120-130 | 130-140 | 140=150 |
Frequency | 12 | 18 | 35 | 42 | 50 | 45 | 20 | 8 |
Cumulative Frequency | 12 | 30 | 65 | 107 | 157 | 202 | 222 | 230 |
Now, N/2 =230/2= 115th item which lies in 110 – 120 group.
Median or 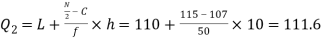
Also, 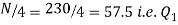 is 57.5th or 58th item which lies in 90-100 group.
is 57.5th or 58th item which lies in 90-100 group.

Similarly 3N/4 = 172.5 i.e. 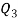 is 173rd item which lies in 120-130 group.
is 173rd item which lies in 120-130 group.

Hence quartile coefficient of skewness = 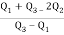
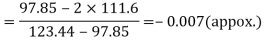
Q24) For a distribution Karl Pearson’s coefficient of skewness is 0.64, standard deviation is 13 and mean is 59.2 Find mode and median.
A24)
It is given that:
Coeff. Of skewness = 0.64, σ = 13 and Mean = 59.2
Therefore by using formula
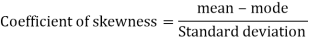
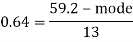

Mode = 59.20 – 8.32 = 50.88
Mode = 3 Median – 2 Mean
50.88 = 3 Median - 2 (59.2)
